带接头管线变形计算的传递矩阵法

程霖 杨成永 路清泉 马文辉 车敬珂

摘   要：地鐵隧道开挖引起邻近地下管线产生附加变形，甚至造成管线破坏. 将带接头地下管线视为弹性地基梁，将接头简化为“自由铰”与“弹簧铰”. 基于Winkler地基模型列出管线变形的控制微分方程，采用传递矩阵法求解，推导了管节场矩阵和管线接头点矩阵，得到关于微分方程未知边值的线性方程组.收集了现场实测数据并进行案例计算和离心模型试验，将本文方法计算结果与有限元法、实测数据和试验结果进行对比，验证了计算模型和传递矩阵法的正确性. 对管线变形的影响因素进行了参数分析，结果表明，对于接头变形，隧道中线与接头位置重合为最不利工况.在土质地层中，自由铰相对转角基本不受地基系数影响，因而自由铰管线易产生较大的相对转角. 管节长度为沉降槽宽度系数的1.6倍时，接头相对转角出现峰值. 接头归一化相对转角的极限值为1.1，在缺少设计资料情况下，该值可作为接头归一化相对转角的保守估计值.

关键词：地下管线;接头;相对转角;弹性地基梁;传递矩阵法

中图分类号：U455                                   文献标志码：A

Transfer Matrix Method for Calculating Deformation of Jointed Pipeline

CHENG Lin1，2，YANG Chengyong1，LU Qingquan3？覮，MA Wenhui1，CHE Jingke4

（1. School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China;

2. China Construction 2nd Engineering Bureau Ltd，Beijing 100160，China;

3. Beijing Metro Construction Administration Co Ltd，Beijing 100068，China;

4. Beijing General Municipal Engineering Design & Research Institute Co Ltd，Beijing 100082，China）

Abstract：Excavation of subway tunnels often causes additional deformation or even damage of adjacent underground pipelines. The jointed pipeline can be regarded as a beam on an elastic foundation. The joints were simplified as "free hinge" and "spring hinge". Based on Winkler's foundation model，a governing differential equation for calculating the pipeline deformation was given and solved by the transfer matrix method. The field matrix for pipeline sections and the point matrix for pipeline joints were derived，and the linear equations for unknown boundary values of the differential equation were obtained. Case calculation and centrifugal model test were conducted and in-situ data were collected. Through comparing the calculation results of this paper with these of finite element method，as well as with in-situ data and test results，the correctness of the calculation model and the transfer matrix method was verified. Parametric analysis of the factors influencing pipeline deformation was carried out. The results show that the worst situation for joint deformation is that the tunnel centerline is right below the joint. The relative rotation angle of the free hinge is hardly affected by the foundation coefficient in the soil stratum. Therefore，the pipeline with a free hinge is easy to have a large relative rotation angle. The peak value of the relative rotation angle appears when the length of the pipeline segment is times of the width coefficient of the settlement trough. The limit of the normalized relative rotation angle is 1.1. This limit can be used as a conservative estimate of the normalized relative rotation angle in the case of a shortage of design data.

Key words：buried pipeline;joint;relative rotation angle;beam on elastic foundation;transfer matrix method

地铁隧道施工使得邻近既有地下管线产生附加变形，造成管线破损，甚至引发工程事故[1]. 为保证隧道开挖不影响管线的正常使用，需要对管线进行安全评价，进而完善设计与施工方案.

地下管线的安全评价指标为地铁施工引起的附加变形[2]. 匀质管线变形的计算方法，一般将管线简化为刚度连续的匀质杆件[3]，承受隧道开挖引起的地层附加位移荷载. 由于管线接头力学性能复杂，带接头管线的变形计算常采用经验方法，假设管节为完全刚性，接头能够自由转动，管线接头沉降与地层沉降一致，根据几何关系推算接头相对转角[2，4]. 经验方法忽略了管线与地层的相互作用，也没有考虑接头传递弯矩的能力. 在理论计算方面，接头的存在使得管线刚度不连续，难以获得管线变形的解析解，因而多采用数值方法求解，解析计算方面的研究较少. Klar等[5]采用边界积分法求解隧道施工引起的管线变形，将管线接头简化为具有转动刚度的弹簧铰单元.张陈蓉等[6]基于有限差分法，在管线接头两侧设置虚节点，给出了带接头管线变形微分方程的差分格式.程霖等[7]在管线变形微分方程中引入脉冲函数，得到了包含傅里叶级数的接头相对转角解析解，虽然考虑了接头处管线抗弯刚度的折减，但刚度折减系数不容易获得，因而不便于实际应用.

以上研究工作表明，目前带接头管线变形计算依赖于经验方法和数值方法，解析方法的研究尚不充分.为此，本文建立带接头管线变形的控制微分方程，从求解微分方程的角度，采用传递矩阵法[8]，推导了管节的场矩阵及管线接头的点矩阵，得到带接头管线状态变量的传递矩阵，进而求得管线变形和内力. 通过与有限元解、经验方法、试验及实测数据的对比，验证了本文方法的正确性，进一步采用本文方法对管线变形的影响因素进行了参数分析.本文方法可用于计算带接头管线的变形和内力，为穿越管线施工的风险评估提供了理论参考.

1   管节和场矩阵

图1为管线变形示意图，隧道开挖引起地层及管线产生沉降，接头处产生相对转角.

将管节视为弹性地基上的Euler-Bernoulli梁，基底变形服从Winkler假定，则管节变形的控制微分方程可写为[7]：

式中：Ep为管线弹性模量，Pa;Ip为管线截面惯性矩，m4;k为地基系数，Pa/m;D为管线外径，m;w和S分别为管线挠度和地层位移，向上为正，m.

地基系数k通过式（2）进行计算[4]，即：

式中：Es为管线所在地层土体的弹性模量，Pa;νs为管线所在地层土体的泊松比.

地层位移用Peck公式表示[9]，即：

式中：Smax为地层最大沉降，m;μ为隧道中线的坐标，m;i为沉降槽宽度系数，m.

如图2所示，将一段管节划分为n小段梁，每小段梁长度为ξ，当ξ比较小时，每小段梁受到的荷载近似为均布荷载.

对图2中任意一小段梁单独分析，将其受到的均布荷载简记为q，则该小段梁变形控制微分方程为：

将式（4）写成一阶微分方程组形式

式中：θ为转角，以逆时针为正，rad;M为弯矩，以使梁下侧受拉为正，N·m;Q为剪力，以使截面右侧梁段顺时针旋转为正，N.

将式（5）改写为矩阵形式

其中：

对式（6）进行拉普拉斯变换，得到：

v（s） = （Is - u）-1 v（0） + （Is - u）-1 l（s）     （7）

式中：s为复变量;I为4阶单位矩阵.

对式（7）进行拉普拉斯逆变换，得到：

v（x） = L-1[（Is - u）-1]v（0） + L-1[（Is - u）-1]v（s）

（8）

式中：L-1[·]为拉普拉斯逆变换运算符.

将坐标x = ξ代入式（8），并将式（8）改写为增广矩阵形式，即：

Vξ = UV0            （9）

其中：

V0 = （w0   θ0   M0   Q0   1）T

Vξ = （wξ    θξ   Mξ   Qξ   1）T

式中：U为场矩阵;V0、Vξ为状态向量，其元素为状态变量，下标表示状态向量和状态变量的计算位置;λ、β1、β2、β3、β4为系数，分别为：

β1 = cos λξ cosh λξ

β2 = sin λξ cosh λξ + cos λξ sinh λξ

β3 = sin λξ sinh λξ

β4 = sin λξ cosh λξ - cos λξ sinh λξ

由式（9）可見，状态向量V0通过矩阵U传递至x = ξ处，得到状态向量Vξ . 通过上述方法获得各小段梁场矩阵，分别记为U1、U2、…、Un，则x = 0处状态变量可依次通过各小段梁场矩阵传递至x = xn处，即

V xn = Un Un - 1Un - 2 …U2 U1 U0 = UV0        （10）

式中：U为整段管节的传递矩阵.

2   接头和点矩阵

将接头简化为铰点，如图3所示，图中，ks为接头转动刚度，N·m/rad;Xj为接头坐标，j为接头编号.将管线接头分为两类，一类不能传递弯矩，两侧管节能够自由转动，将这种接头简化为自由铰，采用此类接头的管线简称“自由铰管线”;另一类能够传递部分弯矩，将这种接头简化为具有一定转动刚度的弹簧铰，采用此类接头的管线简称“弹簧铰管线”.

铰点左侧状态变量通过铰点传递至右侧，即：

铰点两侧管线的挠度、弯矩和剪力均相同，管线转角将产生突变.

对于弹簧铰，转角突变Δθ等于弯矩与接头转动刚度的比值，即弹簧铰两侧转角的关系为：

因此，任意一个弹簧铰的点矩阵为：

对于自由铰，设第j个接头右侧转角为：

θRXj = θLXj + ΔθXj = θLXj + ηθw wLXj + ηθθ θLXj +

ηθM MLXj + ηθQ QLXj + ηθq qLXj          （13）

式中：ηθ为各状态变量以及外力对管线转角的影响系数，则第j个接头的点矩阵可表示为：

根据式（11），第j个接头两侧状态向量关系为：

将式（14）代入式（10），得到第j+1个接头左侧的状态向量

式中：Uj + 1为第j个接头右侧管节的传递矩阵，设为：

Uj + 1 = uww    uwθ     uwM    uwQ    uwquθw    uθθ      uθM    uθQ    uθquMw    uMθ     uMM   uMQ    uMquQw    uQθ     uQM    uQQ    uQq 0       0       0       0      1

uMw + uMθ ηθw = 0uMθ + uMθ ηθθ = 0uMM + uMθ ηθM = 0uMQ + uMθ ηθQ = 0uMq + uMθ ηθq = 0          （16）

解方程组（16）可得影响系数ηθ的值，进而得到第j个接头的点矩阵，即：

3   边界条件和状态变量求解

对于计算长度为L、管节数为N + 1、接头数目为N的管线，如图4所示，管线左端（x = 0）的状态变量可依次通过管节的场矩阵和接头的点矩阵传递至管线右端（x = L），即：

式中：Ue为总体传递矩阵.

计算范围内管线两端距离隧道穿越中线较远，受隧道开挖影响可以忽略不计.

对于弹簧铰管线，根据其接头特点，令管线两端转角为0，剪力为0，则左端的状态向量为：

V0 = （w0   0   M0   0   1）T

其中，w0、M0为管线左端未知状态变量.通过式（17）将V0传递至管线右端，利用管线右端转角为0，剪力为0的边界条件，得到关于未知状态变量的方程组

f1（w0，M0） = 0f2（w0，M0） = 0       （18）

对于自由铰管线，根据其接头特点，令管线两端沉降为0，弯矩为0. 则左端的状态向量为：

V0 = （0   θ0   0   Q0   1）T

其中，θ0、Q0为管线左端未知的状态变量.

要注意，在推导第N个接头点矩阵N时用去了管线右端弯矩为0的边界条件，管线右端只剩下沉降为0这一个边界条件可以利用，弯矩为0的条件只剩下第1个接头处可以利用.因此，分别通过式（10）和式（17）将V0传递至第1个接头（x = X1）和管线右端，利用第1个接头处弯矩为0的条件和管线右端竖向变形为0的条件，得到关于左端未知状态变量的方程组

g1（θ0，Q0） = 0g2（θ0，Q0） = 0       （19）

求解方程组（18）或方程组（19）得到x = 0处未知状态变量，再通过场矩阵和点矩阵计算管线各点的变形和内力. 隧道开挖引起的管线相对转角等于接头两侧管节的转角差值，即

ΔθXj = θRXj - θLXj         （20）

從求解过程看，与有限元法相比，传递矩阵法的未知量只有管线两端的未知边值，无需求解大型方程组，计算量小，且可通过增减分段数达到任意计算精度.从所需计算参数看，与文献[7]的傅里叶级数法相比，传递矩阵法采用的接头转动刚度可通过现有资料获得[10]，便于实际应用.

4   案例计算与试验验证

4.1   案例计算

采用MATLAB编写本文方法的计算程序.为验证本文方法的正确性，采用ANSYS建立有限元模型，其中管节采用梁单元（BEAM4）模拟，地基弹簧和管线接头采用弹簧单元（COMBIN14）模拟.地基弹簧单元的一端与梁单元节点相连，另一端施加由隧道开挖引起的地层位移荷载.

案例1为文献[4]算例，隧道垂直下穿管线，计算参数为：地层最大沉降13.6 mm，沉降槽宽度系数2.6 m，地基系数2.38 × 107 Pa/m;管线弹性模量70 GPa，外径0.5 m，壁厚0.018 m;管节长度5.49 m，管线接头简化为自由铰.

案例2为北京地铁14号线某区间工程垂直下穿铸铁污水管线，测得地层最大沉降12.4 mm，沉降槽宽度系数2.5 m，地基系数2.66 × 107 Pa/m;管线弹性模量100 GPa，外径1.462 m，壁厚17.1 mm;管节长度6 m，接头转动刚度1.79 × 107 N·m/rad.

图5为管线沉降和弯矩的计算结果，同时也给出了与有限元结果及实测数据的对比.可见，本文方法计算结果与有限元方法结果一致，与实测数据趋势基本符合，证明了本文方法的正确性.

文献[4]给出的经验方法未考虑管土相互作用，简单假定管线接头处的沉降与同水平处地层自由沉降一致，得到最大相对转角计算结果为4.42 × 10-3 rad（0.25°）. 由于管节本身具有一定的抗弯刚度，因而管线接头沉降与地层沉降并不相同，本文方法考虑了管土相互作用，所得隧道正上方接头沉降大于同水平处地层自由沉降，最大相对转角的计算结果为4.96 × 10-3 rad（0.28°），由此可见，本文方法与经验方法相比更为安全、合理.

4.2   离心模型试验

试验采用交通运输部天津水运工程科学研究院的TK-C500型土工离心机，设计加速度为80g（由π定理可知模型的几何相似数为80[11]），模拟盾构隧道垂直下穿既有管线，如图6所示.

如图6所示，采用LVDT位移传感器测量管线沉降及管轴线同一水平处土层沉降. 设置11个弯矩测量断面，每个测量断面用4个应变片连接成全桥电路.

试验管线为承插式铝合金管.试验隧道开挖采用外套钢套筒的液压油缸模拟，套筒可沿油缸纵向滑动，推出套筒将引起地层损失从而使地层及管线产生变形. 将管线与隧道的模型及原型试验参数列于表1.

管线模型包含8个管节，总长922.5 mm，管线模型中心接头与隧道开挖中线重合.在管节承口内部粘贴橡胶圈，将管节插口插入橡胶圈粘牢，如图7所示，室内试验测得接头旋转刚度为4.76 × 108 N·m/rad.试验用土为丰浦砂，室内试验测得地基系数为7.37 × 106 Pa/m.

试验时，逐级增大离心机加速度至80g，待管线与土层沉降稳定，将钢套筒按40 mm/min的速度匀速推出，模拟隧道开挖，管土沉降稳定后逐渐降低离心机加速度至停止.

将隧道开挖引起的管轴线同一水平处土体自由沉降监测数据按式（3）拟合，得到Smax = 73.31 mm，沉降槽寬度i = 6.60 m. 采用地层沉降拟合数据（已换算为原型沉降数据）计算管线沉降和弯矩，与试验结果进行对比，如图8所示，可见，管线沉降和弯矩的理论计算结果与试验数据趋势一致，相互能够进行较好的印证.

5   影响因素分析

5.1   接头与隧道中线相对位置的影响

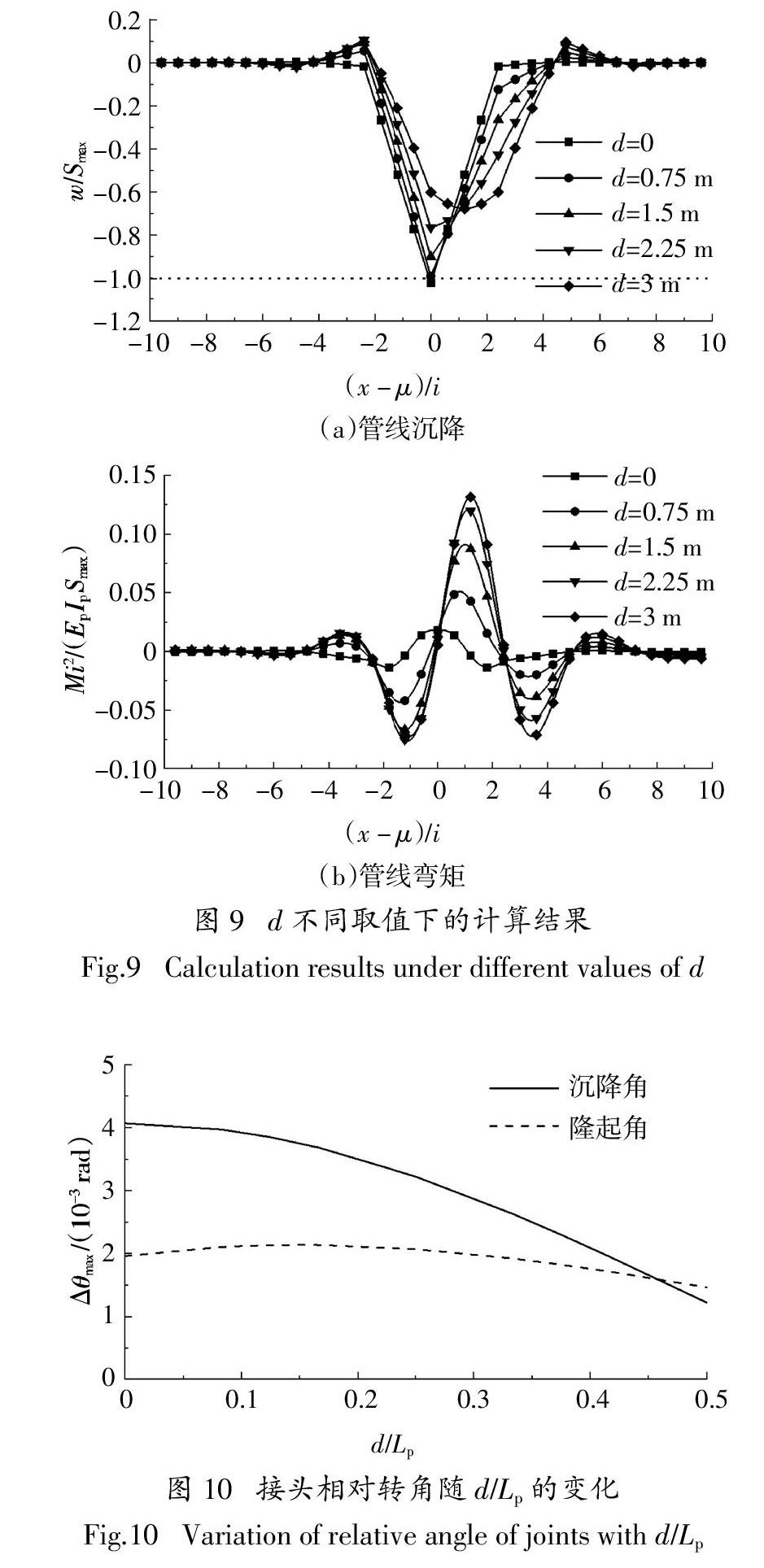
设接头与隧道中线距离为d，管节长度为Lp，则案例计算相当于考虑了d = 0和d = 0.5Lp两种位置关系.为更全面了解接头与隧道中线相对位置对管线变形和内力的影响，令d = 0、0.75 m、1.5 m、2.25 m、3.0 m，结合案例2计算参数，计算管线变形和弯矩.

将位置坐标x、管线沉降w和弯矩M归一化，得到无量纲量（x - μ）/i、w/Smax和Mi2/（Ep Ip Smax），计算结果如图9所示，可见，d = 0时，隧道中线处管线沉降大于地层沉降，两侧相邻管节变形呈现刚体转动，管线弯矩较小. 随隧道中线向管节中部移动，管线沉降减小，隧道中线附近管节弯曲变形增大，管线弯矩增大. 图9（a）表明，距离隧道中线最近的管线接头产生的相对转角最大，该处接头相对转角是由管线沉降造成的，本文称为“沉降角”;距离隧道中线2.5i～3.5i范围内，管线产生一定的隆起变形，该处管线接头也产生明显的相对转角，本文称为“隆起角”.

图10为管线“沉降角”和“隆起角”的最大值随d/Lp的变化规律. 由图10可见，“沉降角”和“隆起角”随d/Lp的增大都呈减小的趋势，因而，对接头变形来说，隧道中线与某一接头位置重合为最不利工况. d/Lp = 0.5时，“隆起角”大于“沉降角”，说明新建隧道中线位于管节中心时，应关注沉降槽边缘（沉降槽半宽约为3i[4]）管线接头产生的“隆起角”.

5.2   地层变形及管线参数的影响

管线的力学响应受地层变形及管线自身参数的影响，包括接头转动刚度ks、管线抗弯刚度Ep Ip、地基系数k、管节长度Lp、沉降槽宽度系数i和地层最大沉降Smax.

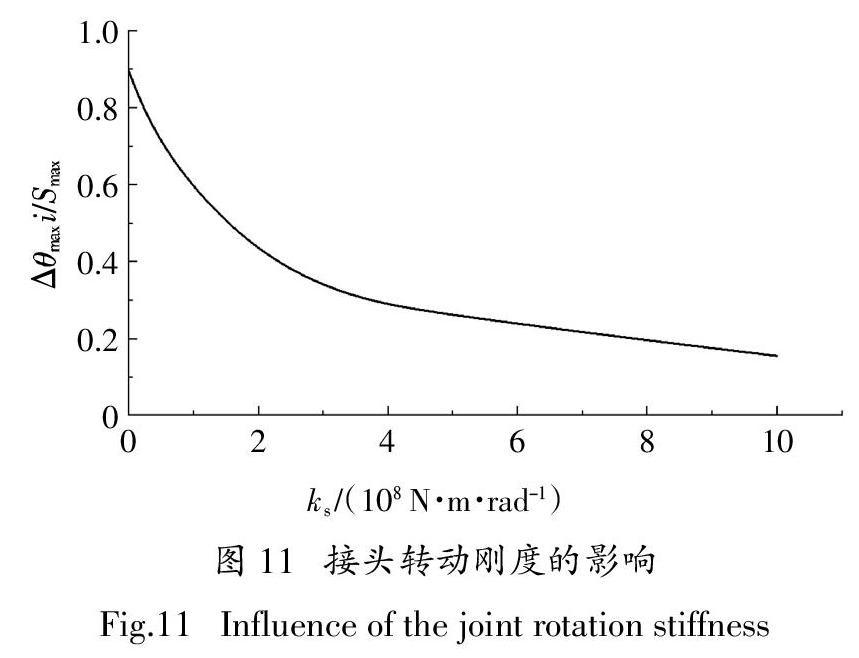
令管线接头处在隧道中线正上方，即最不利位置.将接头最大相对转角归一化，即Δθmax i/Smax，结合案例2计算参数，讨论以上参数对其影响.

图11给出了归一化最大相对转角随接头转动刚度ks的变化规律. 由图11可见，接头转动刚度为0时，接头不承受弯矩，此时接头相对转角最大;随接头转动刚度的增大，接头承受弯矩的能力增强，接头相对转角减小.

图12 ～ 图14分别给出了两类管线归一化最大相对转角随地基系数k、管节抗弯刚度Ep Ip和管节长度Lp的变化规律.由图12可见，接头相对转角随地基系数的增大呈先增大后减小的趋势. 这是因为地基系数较小时，管节弯曲变形由接头转动释放，管节变形呈刚性，在接头两侧产生转角差异，此时地基系数增大使管线沉降增大，进而接头两侧管节的转角差异增大;地基系数较大时，随地基系数增大，管节的弯曲变形增大，接头两侧管节的转角差异减小.对于自由铰管线，相对转角在k = 1 × 106 ～ 2 × 108 Pa/m范围内（大部分土质地基的地基系数位于此范围[12]）变化不大，可以推断，在土质地层中，不论土体压缩性如何，自由铰管线均易于产生较大的接头相对转角.

由图13可见，两类管线受管节抗弯刚度的影响相同. 管节刚度较小时，管线整体变形与地层变形接近，变形曲线平缓，接头相对转角较小;管线刚度较大时，管节呈刚体转动，管线变形与地层变形差异较大，接头产生较大的相对转角.

由图14可见，两类管线受管节长度的影响相同.管线被接头划分为若干小段，管节长度较小时（Lp < 1.6i），整体变形呈现柔性，变形与地层变形接近，在这个阶段，随管节长度增长，管线整体性增强，与地层变形差异增大，接头相对转角也增大;由于管节具有一定的抵抗弯曲变形的能力，管节长度较大时（Lp > 1.6i），随管节长度增长，管线沉降减小，接头相对转角也减小;管节长度为1.6i时，接头相对转角达到峰值. 在实际工程中，应对管节长度满足这一特征的管线予以重视，加强防护和监测.

由图12～图14可以看出，归一化相对转角存在极限值，不会随某一计算参数的增长而无限增长.为得到归一化相对转角的极限值，计算自由铰管线归一化最大相对转角随地层变形参数Smax和i的变化规律，如图15、图16所示.

由图15可见，归一化相对转角不随地层最大沉降的变化而变化，说明接头相对转角与地层最大沉降呈正比. 由图16可见，随沉降槽宽度系数的增大，归一化最大相对转角呈先增大后减小的趋势，这是因为沉降槽宽度较小时，管线由于自身刚度的原因，变形小于地层沉降;随着沉降槽宽度增大，管线变形超过地层沉降，接头相对转角增大，但沉降槽宽度的增大使得地层沉降逐渐平缓，管线变形逐渐与地层沉降趋于一致，接头相对转角减小. 通过图16可以看出，管线归一化相对转角的极限为1.1，当实际工程中缺乏设计资料时，可取Δθmax = 1.1 Smax /i作为保守的接头相对转角估计值.

6   结   论

将带接头管线按接头传递弯矩的特性分为“自由铰管线”和“弹簧铰管线”两类. 采用传递矩阵法求解了管线变形的控制微分方程，推导了管节的场矩阵和两类管线接头的点矩阵，给出了管线未知边值的求解过程. 通过与有限元计算结果、离心模型试验结果和实测数据对比，本文方法是可靠的.

采用本文方法针对管线接头与隧道开挖中线距离、管线参数和地层变形参数进行了影响因素分析.结果表明，对接头变形来说，接头与隧道中线位置重合为最不利工况.若隧道中线位于管节中心，则距开挖中线2.5i ～ 3.5i的管线接头将因此处的管线隆起而产生较大的相对转角.相同条件下，自由铰管線的接头相对转角大于弹簧铰管线.在土质地层中，自由铰管线可产生比较大的接头相对转角，且相对转角基本不受地基系数影响.通过分析管节长度的影响规律，可知管节长度为1.6i时，接头相对转角出现峰值，实际工程中应对符合这一长度特征的管线采取相应的保护措施，并加强监测. 参数分析表明，管线接头相对转角的极限值为1.1Smax /i，当缺乏设计资料时，可用该值保守估计管线相对转角.

参考文献

[1]    HOU Y J，FANG Q，ZHANG D L，et al. Excavation failure due to pipeline damage during shallow tunnelling in soft ground[J]. Tunnelling and Underground Space Technology，2015，46：76—84.

[2]    李兴高，王霆. 柔性管线安全评价的简便方法[J].岩土力学，2008，29（7）：1861—1864.

LI X G，WANG T. Simple method for evaluating safety of flexible pipelines[J]. Rock and Soil Mechanics，2008，29（7）：1861—1864. （In Chinese）

[3]    杨成永，寇鼎涛，程霖，等. 对称荷载作用下弹性地基梁的傅里叶级数解[J]. 湖南大学学报（自然科学版），2018，45（3）：136—141.

YANG C Y，KOU D T，CHENG L，et al. Fourier series solution for elastic foundation beams under symmetric loads[J]. Journal of Hunan University （Natural Sciences），2018，45（3）：136—141. （In Chinese）

[4]    ATTEWELL P B，YEATS J，SELBY A R. Soil movements induced by tunnelling and their effects on pipelines and structures[M]. London：Blackie and Son Ltd，1986：153—156.

[5]    KLAR A，MARSHALL A M，SOGA K，et al. Tunneling effects on jointed pipelines[J].Canadian Geotechnical Journal，2008，45（1）：131—139.

[6]    张陈蓉，俞剑，黄茂松. 隧道开挖对邻近非连续接口地埋管线的影响分析[J]. 岩土工程学报，2013，35（6）：1018—1026.

ZHANG C R，YU J，HUANG M S. Responses of adjacent underground jointed pipelines induced by tunneling[J]. Chinese Journal of Geotechnical Engineering，2013，35（6）：1018—1026. （In Chinese）

[7]    程霖，杨成永，李延川，等. 带接头地下管线变形的傅里叶级数解[J]. 湖南大学学报（自然科学版），2018，45（11）：149—156.

CHENG L，YANG C Y，LI Y C，et al. Fourier series solution for deformation of buried jointed pipelines[J]. Journal of Hunan University （Natural Sciences），2018，45（11）：149—156. （In Chinese）

[8]    劉庆潭，倪国荣. 结构分析中的传递矩阵法[M]. 北京：中国铁道出版社，1997：1—4.

LIU Q T，NI G R. Transfermatrix method in structural analysis [M]. Beijing：China Railway Publishing House，1997：1—4. （In Chinese）

[9]    OREILLY M P，NEW B M. Settlements above tunnels in the United Kingdom—their magnitude and prediction[C]// Proceedings of the 3rd International Symposium. London：Institution of Mining and Metallurgy，1982：173—181.

[10]  SINGHAI A C. Behavior of jointed ductile iron pipelines[J]. Journal of Transportation Engineering，1984，110（2）：235—250.

[11]  杜延龄，韩连兵. 土工离心模型试验技术[M]. 北京：中国水利水电出版社，2010：16—29.

DU Y L，HAN L B. Geotechnical centrifugal model test technology[M]. Beijing：China Water & Power Press，2010：16—29. （In Chinese）

[12]  中国船舶工业总公司第九设计研究院.弹性地基梁及矩形板计算[M]. 北京：国防工业出版社，1983：288—289.

Ninth Design and Research Institute，Chinese Shipbuilding Industry General Corporation. Calculation of beam on elastic foundation and rectangular plate [M]. Beijing：National Defense Industry Press，1983：288—289. （In Chinese）