基于低功耗有损网络路由协议的多路由度量评估算法*

曹亚楠，原 豪

(1.天津师范大学电子与通信工程学院，天津 300387；2.中国人民解放军 61846部队，河北 涿州 072750)

低功耗有损网络路由协议(RPL，Routing Protocol for Low-power and Lossy Networks)[1]是由IETF(IETF，Internet Engineering Task Force)专门制定的适用于低功耗有损网络的一种距离矢量路由协议。该协议充分考虑了链路有损，链路不稳定，带宽有限，节点的处理能力有限，节点的能量有限以及节点的存储能力有限等低功耗有损网络特点，选择最优路径传输数据，从而改善网络寿命、时延等性能。在军事侦查、农业生产、野生动物监测、智能电网以及智能家居等领域有广阔的应用前景。

路由度量(RM，Routing Metric)[2]是构造目标函数、计算路径开销以及选择最优路径的一项重要依据。IETF发布的RFC6551中详细说明了RPL可采用的路由度量及计算方法。如OF0(OF0，Objective Function)[3]是依据跳数计算最优路径。目前，低功耗有损网络路由协议的应用前景广阔且多样，仅依据单一方面的路由度量计算最优路径已无法满足现有的各类应用需求。因此，针对不同的应用需求综合评估多方面的路由度量，可有效地改善网各方面的性能。

尽管评估多个路由度量可有效改善网络性能，一定程度上满足某些领域的应用需求，但尚未实现有效地应用和推广，主要是因为缺乏系统且科学的多路由度量评估方法理论依据。因此，为多路由度量评估方法提出科学且合理的理论依据，是改善网络性能满足各领域的应用需求的科学途径，具有重要的理论意义和现实价值。为此，本文针对RPL提出一种基于组合赋权法和逼近理想解排序法(TOPSIS，Technique for Order Performance by Similarity to Ideal Solution)的多路由度量评估算法—MRM-CT(MRM-CT，Multiple Routing Metrics evaluation algorithm based on Combination weighting method and TOPSIS)，主要研究工作如下:①提出应评估的路由度量主要有ETX、缓存占用率，节点剩余能量、跳数和时延，并对它们进行标准化处理；构建邻居节点关于各路由度量的初始判断矩阵。②依据初始判断矩阵，构建包含上述各路由度量的复合目标函数。③提出采用兼顾主客观因素的组合赋权法确定复合目标函数中各路由度量的权重。④基于各权重信息和复合目标函数，提出采用逼近理想解排序法确定最优的下一跳节点，从而有效优化最优路径的选择，显著提升网络性能。⑤仿真结果表明，本文提出的MRM-CT算法可显著改善分组投递成功率、时延等各方面的性能，优于现有的RPL及其相关改进算法。

本文后续部分内容安排如下:第1部分简述RPL以及现有相关算法存在的问题；第2部分详述新提出的MRM-CT算法；第3部分进行仿真实验及结果分析；最后第4部分总结全文并简介未来研究工作。

1 RPL简介及存在的问题

1.1 RPL简介

RPL主要通过一组控制消息、各种路由度量以及目标函数构建网络拓扑并进行信息交互。

①路由度量

路由度量是用于计算最短或最小开销路径的依据。现有的路由协议可同时依据多个路由度量计算最优路径。目前路由度量可分为节点路由度量和链路路由度量两类。节点路由度量主要有节点状态和属性(NSA，Node State and Attribute)、节点的剩余能量、节点到目的节点所需的跳数、节点的子节点数等。链路路由度量主要有吞吐量、时延、ETX和LQL(LQL，Link Quality Level)等。

②目标函数(OF，Objective Function)

目标函数[4]是低功耗有损网络路由协议的重要工具之一，主要用于规定如何将几个路由度量组合成复合目标函数，并将其转化为节点的秩(Rank)值，而节点的秩也是构建和维护网络拓扑，选择最优路径等的依据。此外，目标函数可根据实际的网络应用需求设计不同的最优路径选择规则。如

MRHOF(Minimum Rank with Hysteresis Objective Function，MRHOF)是依据ETX选择最优路径。它是一种具有滞回功能的目标函数，避免因为路由度量的轻微变化而引起网络拓扑的抖动。

③控制消息

RPL中用到的控制消息主要有DIO(DIO，DODAG Information Object)、DAO(DAO，Destination Advertisement Object)、DIS(DIS，DODAG Information Solicitation)及DAO-ACK(DAO-ACK，Destination Advertisement Object Acknowledgement)等[5]。它们相应的功能解释如表1所示。

表1 RPL控制消息

1.2 问题描述

低功耗有损网络路由算法选择下一跳节点时仅评估邻居节点单一方面的路由度量如ETX已无法满足各领域的应用要求。如OF0(Objective Function 0，OF0)基于跳数选择最优路径。ETXOF[6]基于ETX选择最优路径。Xiao W等人[7]提出应依据PER-HOP ETX(一条路径上每条链路所需ETX的均值)而不是各条链路的ETX之和选择最优路径，该方法可有效的避免选中的最优路径中包含个别ETX较大的链路。Sanmartin P等人[8]提出依据SIGMA-ETX方法，SIGMA-ETX依据路径上各条链路ETX的均方差值来选择最优路径。这种单一的路由度量评估方法选择的下一跳节点可能存在剩余能量较低，负载过重等问题，进而影响网络性能，已无法满足无线传感网、智能电网等领域的应用需求。

为此，有研究提出同时评估邻居节点多个方面的路由度量的方法以满足各领域的应用需求。如Zohreh R等人[9]提出评估链路质量、信噪比、节点剩余能量和缓存占用率四个路由度量，并采用蚁群算法实现多个路由度量的评估。Hermano P等人[10]提出NIAP(Network Interface Average Power Metric，NIAP)路由度量，该路由度量通过评估网络接口处的平均能耗和缓存占用率以均衡负载并延长网络寿命。Ajay K等人[11]提出DCRL-RPL(Dual Context-based Routing and Load Balancing in RPL，DCRL-RPL)协议，该协议采用RWR(Random Walk Ranking，RWR)算法评估节点与根节点之间的距离，剩余能量以及负载影响指数三种路由度量以延长网络寿命并均衡负载。Altwassi H S等人[12-14]提出通过联合评估邻居节点的缓存队列长度与其他路由度量以感知拥塞和均衡负载。Behrad B V等人[15]提出将节点的剩余能量除以ETX和时延的乘积作为新的路由度量；Nassar J等人[16]提出采用多实例方法同时评估时延、ETX和节点剩余能量；Hanane L等人[17]列出时延等其他方面的研究现状。Taghizadeh S等人[18-20]提出将节点的剩余能量与其他路由度量综合使用，以判断邻居节点是否具备成为下一跳的能力。而节点剩余能量与其他路由度量的重要程度则由相应的权重系数决定。但各个路由度量权重系数的确定多是基于专家的主观个人经验，尚无合理的权重系数确定理论可依据。Alayed W等人[21]提出采用层次分析法确定目标函数中各路由度量的权重，该方法过于主观。而Hanane L等人[22]提出采用模糊逻辑方法评估ETX和节点剩余能耗。但模糊逻辑方法将信息简单的模糊处理则会降低系统的控制精度和动态品质。

由此可知，现有的多路由度量评估方法考虑路由度量不全面，无法全面综合评估邻居节点成为下一跳节点的能力。且现有的多路由度量评估方法缺乏科学的多路由度量评估理论依据，无法兼顾网络客观因素和人为主观因素，更无法随着网络的运行实时变更各路由度量的重要程度，这在一定程度上影响了网络性能，限制了该协议的推广和应用。综上所述，现有的RPL多路由度量评估算法主要存在以下问题:

①路由度量评估不全面。

现有的改进算法大多仅评估ETX和节点剩余能量，其他方面的路由度量如节点缓存占用率等未均考虑。从而无法兼顾负载均衡、能耗、时延和稳定性等方面的性能，限制了该协议的推广和应用。

②复合目标函数中各路由度量的权重确定方法不科学。

目前复合目标函数中各路由度量权重的确定主要是依据专家的主观经验。该方法过于主观，忽略了网络的客观实际情况，缺乏科学合理的权重分配理论依据。

③下一跳节点的选择机制过于简单简陋。

现有的下一跳节点选择方法多是基于复合目标函数的计算结果。对各邻居节点并未进行正负理想解的排序，在一定程度上会影响下一跳节点的选择，影响网络性能。

为此，本文提出一种基于组合赋权法和逼近理想解排序法的多路由度量评估算法—MRM-CT。MRM-CT可全面综合评估邻居节点各方面的路由度量，采用兼顾主客观因素的组合赋权法确定复合目标函数中各路由度量的权重，并采用TOPSIS法确定最优路径，进而改善网络性能；为多路由度量评估提供一种科学的理论依据。

2 MRM-CT算法设计

2.1 路由度量的选择

为综合评估邻居节点各方面的能力，本文选择同时评估以下五种路由度量:节点剩余能量指数REI(REI，Residual Energy Index)、缓存占用率BOR(BOR，Buffer Occupancy Ratio)、ETX、时 延D(Delay)和跳数(HC，Hop Count)。假设非根节点c有n个候选父节点(邻居节点)，则各个路由度量的标准化处理如下:

①节点剩余能量指数(REI)

REI表示候选父节点的剩余能量指数，其计算方法如式(1)所示。其中Einitial(i)表示候选父节点i的最大初始能量，Ecurrent(i)候选父节点i的当前剩余能量，ip表示候选父节点i的偏好父节点，β＝0.21为调整参数，用于调节i的偏好父节点的影响程度。REI(i)反映了候选父节点i及其偏好父节点ip的剩余能量指数。可见REI(i)以迭代的方式表征了节点的剩余能量。且父节点剩余能量的影响会随着路径的深入而降低。因此REI(i)可用于避免选择较低能量的路径传输数据。

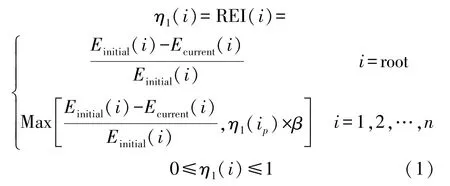
②缓存占用率(BOR)

BOR表示节点的缓存使用情况，可依据式(2)计算。其中Q(i)为缓存指数，根据式(3)计算。ip为候选父节点i的偏好父节点，β＝0.21为调整参数，用于调节i的偏好父节点的影响程度。BOR(i)反映了候选父节点i及其偏好父节点ip的缓存占用率。BOR(i)以迭代的方式表征了节点的缓存占用率，且父节点的缓存占用率的影响会随着路径的深入而降低，因此BOR(i)可用于缓解拥塞和均衡负载。

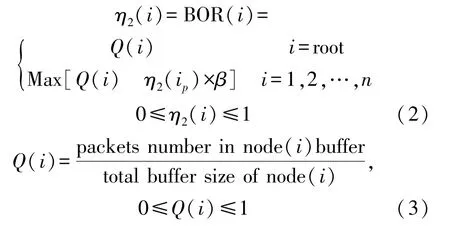
③ETX

依据传统的ETX计算方法，一条路径的ETX等于该路径上所有链路的ETX之和。则最小ETX对应的路径为最优路径。该种最优路径选择方法有可能选择具有较大ETX链路的路径为最优路径。为此本文提出将路径上各条链路的ETX均方差、和值以及均值结合使用的方法。节点c通过候选父节点i到目的节点的路径Pi的ETX和值(ETX(i))、ETX均值和ETX均方差(σETX(i))可分别依据式(4)~式(6)计算。

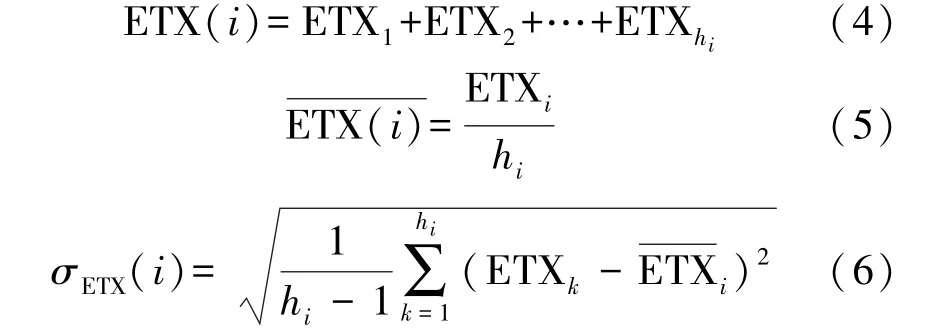
式中:i＝1，2，…，n，hi表示路径Pi所需的跳数。则ETX路由度量的具体使用规则如下:

(a)首先计算从节点c通过各个候选父节点到达目的节点的各条路径所需ETX和值、ETX均值和均方差值。即，(i＝1，2，…，n)}和{σETX(i)， (i＝1，2，…，n)}。

(b)将{ETX(i)，(i＝1，2，…，n)}由小到大排序，取最小的前3个ETX和值对应的路径组成备选路径集合，不足3个的全部选入备选路径集合。

(c)在备选路径集合中，可选择最小ETX均方差对应的路径为最优路径。假设σETX(f)为最小值，则路径Pf(从节点c经过候选父节点f到目的节点)为最优路径，从而候选父节点f为偏好父节点。

这种将ETX和值(ETX(i))、ETX均值和ETX均方差(σETX(i))组合使用的方法既保障了链路质量，又在一定程度上避免了选中的最优路径中存在较大ETX链路的情况。

为便于ETX与其他路由度量联合使用，需对σETX(i)做归一化处理，如式(7)和式(8)所示。

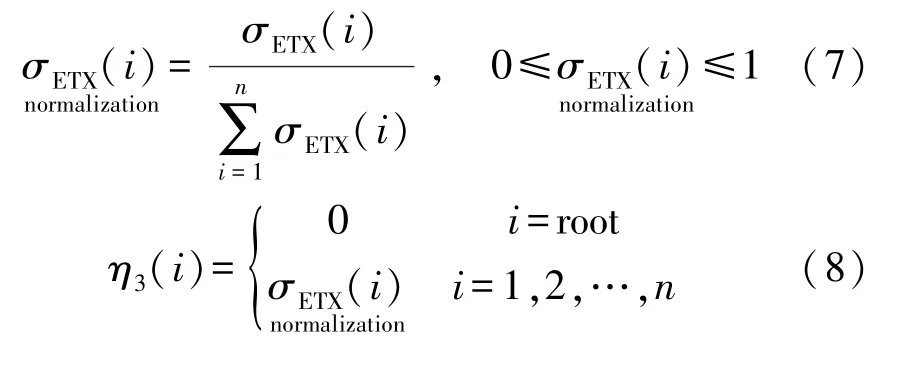
④时延(D)

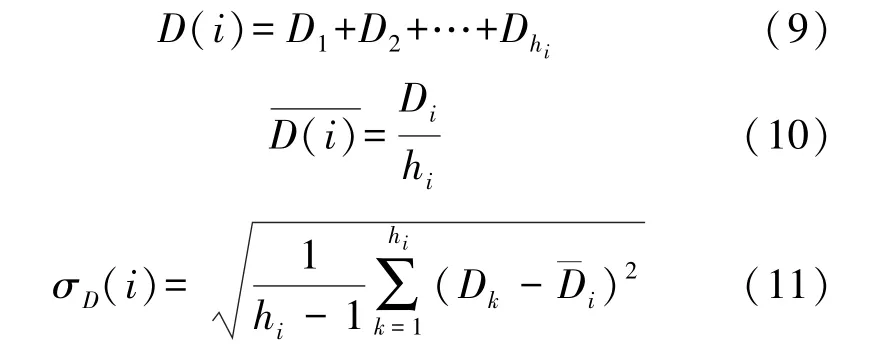
式中:i＝1，2，…，n，hi表示路径Pi所需的跳数。则时延路由度量的具体使用规则如下:

(a)首先计算从节点c通过各个候选父节点到达目的节点的各条路径所需时延和、时延均值和均方差。即{D(i)，(i＝1，2，…，n)}，，(i＝1，2，…，n)}和{σD(i)，(i＝1，2，…，n)}。

(b)将时延和值{D(i)，(i＝1，2，…，n)}由小到大排序，取最小的前3个时延和值对应的路径组成备选路径集合，不足3个的全部选入备选路径集合。

(c)在备选路径集合中，可选择最小时延均方差对应的路径为最优路径。假设σD(f)为最小值，则路径Pf(从节点c经过候选父节点f到目的节点)为最优路径，从而候选父节点f为偏好父节点。

这种将时延和值(D(i))、时延均值和时延均方差(σD(i))组合使用的方法既保障了路径的最小时延，又在一定程度上避免了选中的最优路径中存在较大时延链路的情况。

为便于时延与其他路由度量联合使用，需对σD(i)做归一化处理，如式(12)和(13)所示。

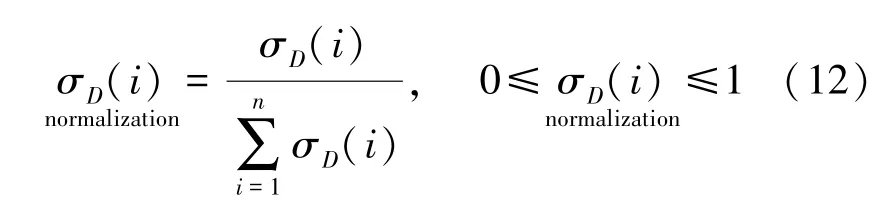
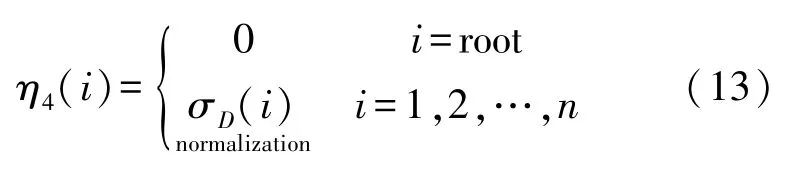
⑤跳数(HC)

跳数表示从候选父节点到根节点之间路径所经过的节点数。该路由度量的使用可避免选择有较大跳数的候选父节点为下一跳节点。跳数在时延和ETX路由度量的均方差计算中均有所考虑，因此本文将不再单独评估跳数度量。

以r1=15 mm，r2=20 mm时得到的粒子速度的频率响应函数为例，按上述分析可得其有效频段的估计值为

上述路由度量对候选父节点各方面的综合评估均有重要影响，MRM-CT采用递归的方法评估节点剩余能量指数和缓存占用率，采用和值、均值和均方差的方法评估ETX和时延，可较好地应用与复合目标函数的构建。

2.2 构建复合目标函数

假设节点c有n个候选父节点，xij表示第i(i＝1，2，…，n)个候选父节点的第j(j＝1，2，…，m)个路由度量指标值。本文主要评估候选父节点的剩余能量指数、缓存占用率、ETX和时延，因此m＝4。则每个候选父节点的各个路由度量的值可表示为样本空间{xij｜i＝1，2，…，n；j＝1，2，…，m}，可记为矩阵形式X，如式(14)所示。则第i个候选父节点的综合评估函数可表示为式(15)。

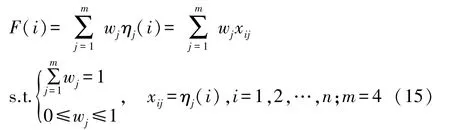
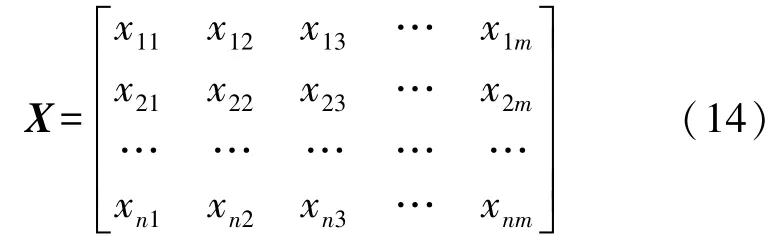
则构造的复合目标函数如式(16)所示。

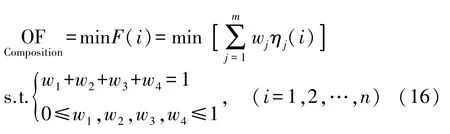
w1、w2、w3和w4为各路由度量对应的权重。可见，复合目标函数中各路由度量权重的科学确定是综合评估候选父节点的重要环节，是确定最优路径的关键。因此科学的确定各路由度量的权重是解决问题的关键。

为此，本文提出采用组合赋权法确定各路由度量的权重系数。组合赋权法[23]是指依据不同赋权方法获取权重后，再依据某种规则将获得的权重重新组合以获得新的组合权重的过程。本文提出的组合赋权法即是将一种主观赋权方法(模糊层次分析法)和一种客观赋权方法(熵值法)分别获得的权重信息，再次融合从而获得一种新的组合权重信息的过程。组合赋权法可解决不同赋权法结果不一致，不同专家评价结果不一致，主、客观权重信息的融合等问题，可利用主、客观赋权法的优点使最终的赋权结果更加的科学和合理。

2.3 组合赋权法确定权重

①主观赋权法(模糊层次分析法)

模糊层次分析法[24]是一种定性与定量分析相结合的方法。该方法确定复合目标函数中路由度量的权重系数的具体步骤如下:

步骤1 构建层次化评价模型

构建的层次化评价模型如图1所示。其中目标层位于层次化评价模型的最顶层，是最终的决策目标，在本文中是指最终选择出的偏好父节点。准则层位于层次化评价模型的中间层，由需要考虑的标准组成，在本文中是指需要评估的路由度量。方案层位于层次化评价模型的最底层，由被评估的具体方案组成，在本文中是指候选父节点。

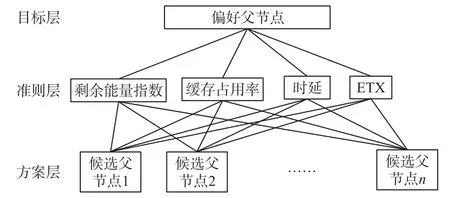
图1 层次化评价模型

步骤2 计算权重系数

(a)计算模糊判断矩阵R＝(ri j)n×m

rij表示本层次中第i个元素与第j个元素之间模糊关系的相关度(即相对重要程度)。为了能够定量地描述任意两个路由度量之间的相对重要程度，本文采用表1所示的0.1-0.9标度法。

表1 0.1-0.9标度法

(b)求解模糊一致性矩阵R′

模糊一致性矩阵R′可根据式(17)和(18)计算。且式(17)可有效的避免了一致性检验过程。

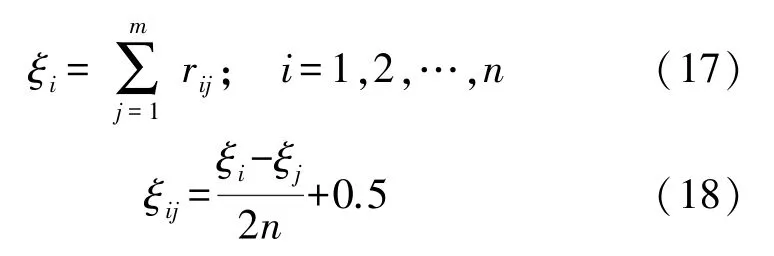
(c)确定权重系数

依据式(18)，对模糊一致性矩阵R′行和归一化处理，确定权重系数wFAHP＝(wFAHP1，wFAHP2，…，wFAHPm)。

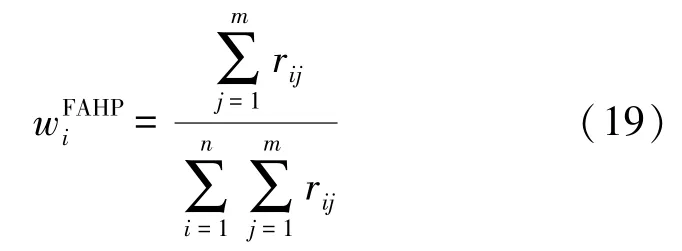
基于上述模糊层次分析法权重系数确定步骤，MRM-CT中具体的依据模糊层次分析法确定权重系操作步骤如下:

步骤1 构建模糊判断矩阵R

依据表1和图1，构造的模糊判断矩阵如式(20)所示。

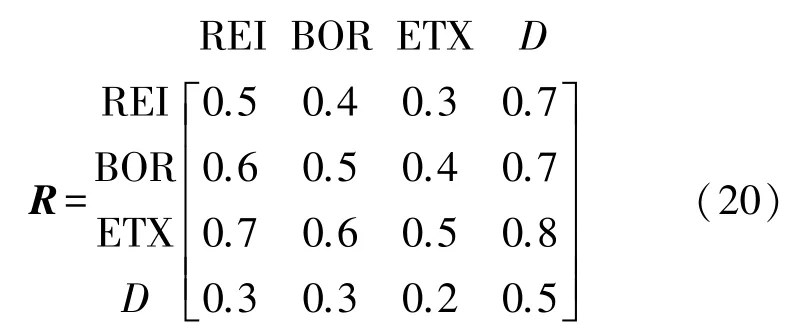
步骤2 计算模糊一致性矩阵R′

依据式(17)和式(18)，模糊一致性矩阵如式(21)所示。

步骤3 计算权重系数

依据式(19)，可求得路由度量的权重系数

步骤4 计算情景感知复合目标函数

依据式(16)，候选父节点i(i＝1，2，…，n)对应的复合目标函数值可表示为:

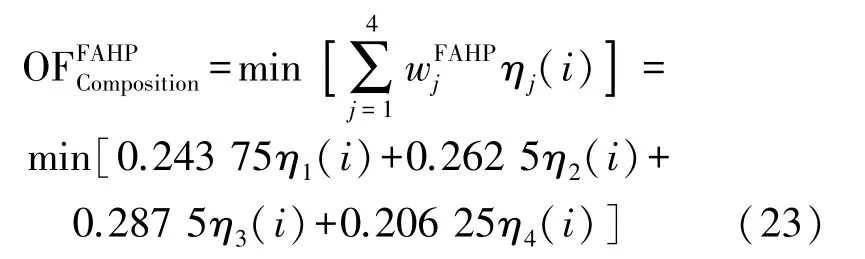
依据模糊层次分析法，选择式(23)最小值对应的候选父节点为偏好父节点。

②客观赋权法(熵值法)

熵值法[25]依据信息论中熵的概念，通过获取指标变化的信息熵值而求得指标的权重。它不受评估主体主观意愿的影响，能够较好地反映指标变化与指标权重的关系，是一种较为理想的客观赋权方法。其核心思想是依据熵的概念和性质以及指标相对重要程度的不确定性来确定各指标的权重。当指标的信息熵较小时，表明指标的变异程度相对较大，包含较大的信息量，在评价过程中起到的作用较大，应分配较大的权重；反之，某指标的信息熵比较大时，其相应的权重应赋较小的权重。

考虑n个方案，m个属性的多属性决策问题，其决策矩阵如式(24)所示，则依据熵值法确定权重的具体计算步骤如下:

步骤1 对各指标同度量化，计算第j项指标下第i个被评价对象的指标值的比重Pij:

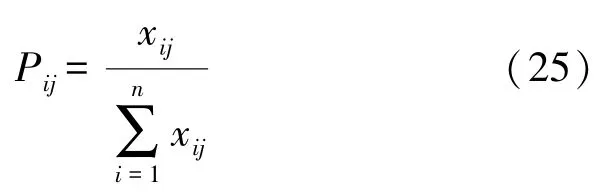
步骤2 计算第j项指标的熵值Ej:

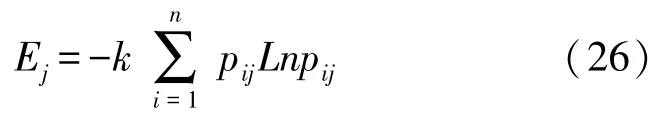
步骤3 计算第j项指标的差异性系数dj并进行归一化处理。

d越大时，指标就越重要。对d进行归一化处理即可得到通过熵值法求得的权重。

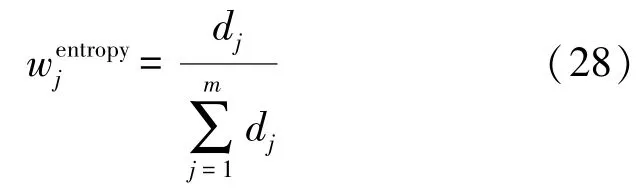
则依据式(16)，候选父节点i(i＝1，2，…，n)对应的复合目标函数可表示为:

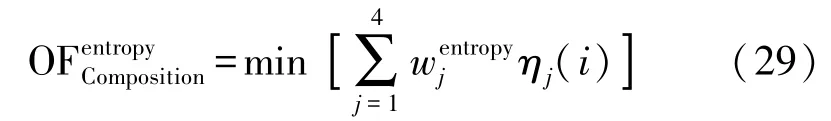
依据熵值法，选择式(29)最小值对应的候选父节点为偏好父节点。

③组合赋权法

组合赋权法以克服主观意愿和客观因素的影响为主要目的，降低主、客观赋权法缺点的影响性，实现二者的优势互补，使得最终求得的组合权重结果既能够反映主体的主观意愿，又能够体现实际的客观信息。

组合赋权法对各种方法求得的权重结果的综合方式一般有乘法合成的归一化法、线性加权组合法和规划法。其中线性加权组合法可克服乘法合成归一化法的“倍增效应”，实际应用效果良好且应用较广泛，因此本文采用线性加权组合法确定最终的组合权重。其具体步骤如下:

步骤1 构建基于线性加权组合法确定组合权重(wj)的数学模型

组合权重的数学模型如式(30)所示。其中，wj表示第j个路由度量最终的组合权重，为通过第k种权重确定方法确定的第j个路由度量的权重，αk为第k种权重确定方法分配的权重系数。

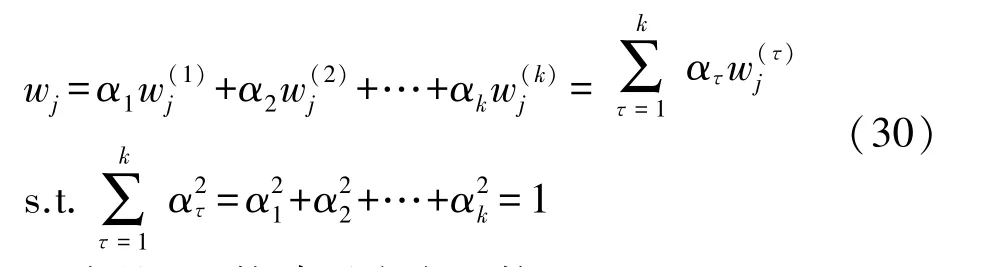
步骤2 构建适应度函数(f(i))

依据式(15)，构造的适应度函数(f(i))如式(31)所示。其中f(i)表示第i个候选父节点的适应度函数值，xij表示第i个候选父节点的第j个路由度量的归一化值。适应度函数(f(i))值越大，表明其对应的候选父节点综合评价值越高，被选为偏好父节点的可能性也越大。

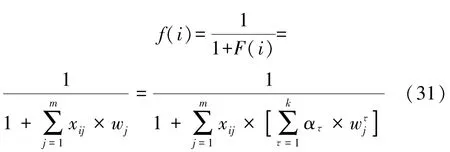
步骤3 构造线性规划模型和最优化模型

基于此，构造的线性规划模型F(i)和最优化模型分别如式(32)和式(33)所示。。

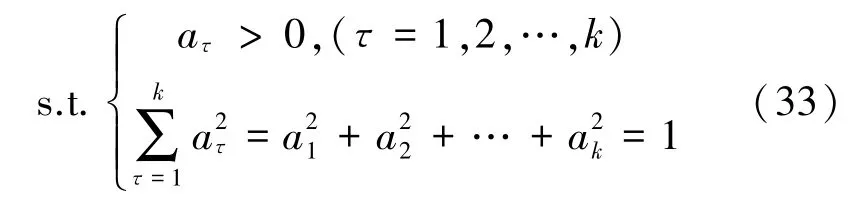
步骤4 通过拉格朗日乘子法计算构造函数中的ατ和λ

(a)基于拉格朗日乘子法建立构造函数

基于拉格朗日乘子法建立的构造函数如式(34)所示。

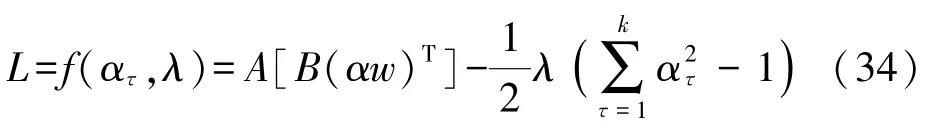
(b)对式(34)中的ατ和λ分别求偏导数，相应的表达式如下:

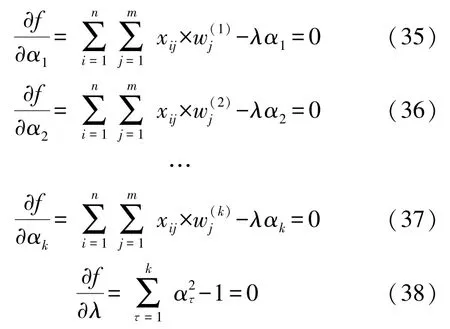
(c)计算ατ

将式(35)~式(37)关于ατ的导函数平方求和可求得，如式(39)所示。

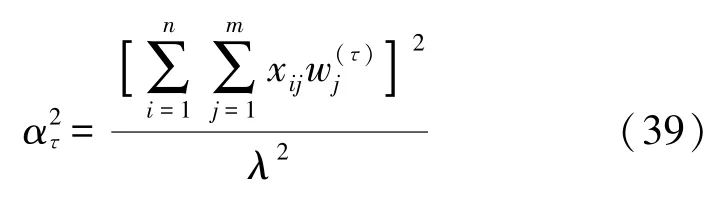
之后，依据式(39)，可求得式(40)。

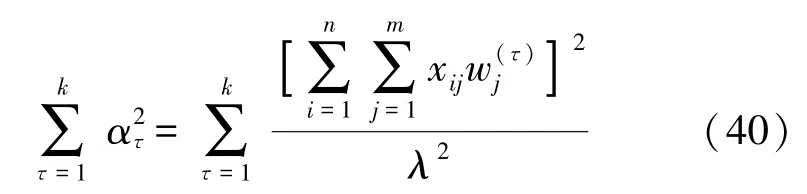
则依据式(38)和(40)，可求得式(41)。

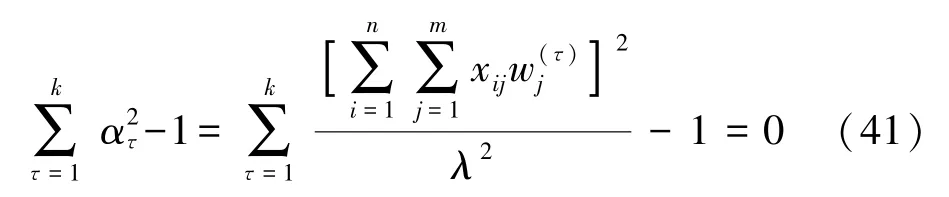
因此ατ可表示为式(42)

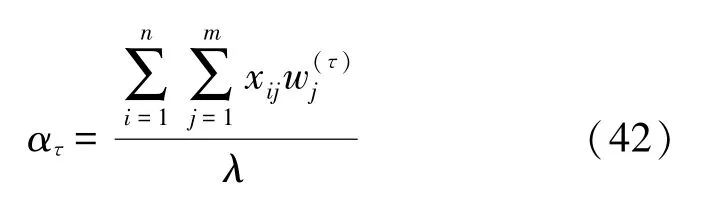
(d)归一化处理ατ

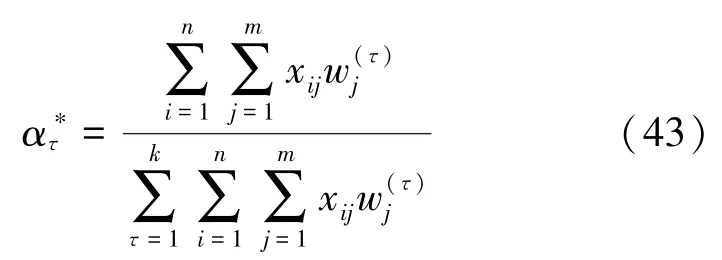
步骤5 计算组合权重

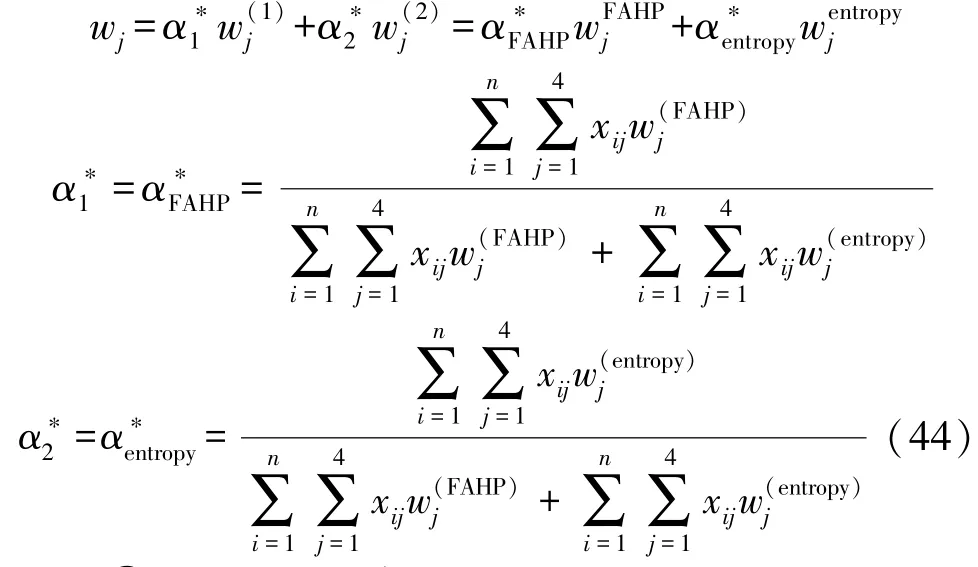
根据式(22)、式(29)和式(43)即可求得最终的组合权重。

本文组合两种赋权方法(模糊层次分析法和熵值法)，因此k＝2。假设，则最终的组合权重表达式如式(44)所示。

④MRM-CT组合赋权法

基于上述内容，MRM-CT采用组合赋权法确定最终权重，并依据此权重计算适应度函数值(式(31))或复合目标函数值(式(16))的具体操作步骤如下:

步骤1 计算主观权重

本文采用模糊层次分析法确定各个路由度量的主观权重，其具步骤作见“①主观赋权法(模糊层次分析法)”部分。

步骤2 计算客观权重

采用熵值法确定各个路由度量的客观权重，其具步骤作见“②客观赋权法(熵值法)”部分。

步骤3 求各权重确定方法对应的权重系数ατ

MRM-CT提出依据拉格朗日乘子法确定ατ。其具体步骤见“③组合赋权法”部分。

步骤4 计算最终的组合权重wj

可依据式(44)计算最终的组合权重wj。

步骤5 计算适应度函数值或情景感知目标函数值

依据式(44)，候选父节点i对应的最终的适应度函数值和复合目标函数值分别如式(45)和式(46)所示。

本文提出的组合赋权法综合了主观赋权法和客观赋权法的优点，实现了二者的优势互补。它不仅克服了主观赋权法不能考虑邻域网的客观应用需求的问题，也在一定程度上解决了客观赋权法不能考虑用户和控制中心等人为主观因素的问题。因此，选择最优路径，显著改善网络性能。此外，组合赋权法也为多个评价指标系统中各个评价指标权重的确定提供了一定的理论依据。

2.4 TOPSIS确定偏好父节点

TOPSIS[26]是一种较直观、精确且适用范围广泛的多属性决策方法。该方法将多个方案与理想化目标的接近程度进行排序，若某方案最接近理想解，且远离负理想解，则该方案较优。

基于上述组合赋权法获得的权重，则通过TOPSIS确定下一跳节点的步骤如下:

步骤1 依据式(14)，计算加权决策矩阵V

式(46)为求得的加权决策矩阵V，其中W为对角矩阵，主对角线上的元素为各个评价指标对应的权重。vij是候选节点i的第j个评价指标的加权标准化值。

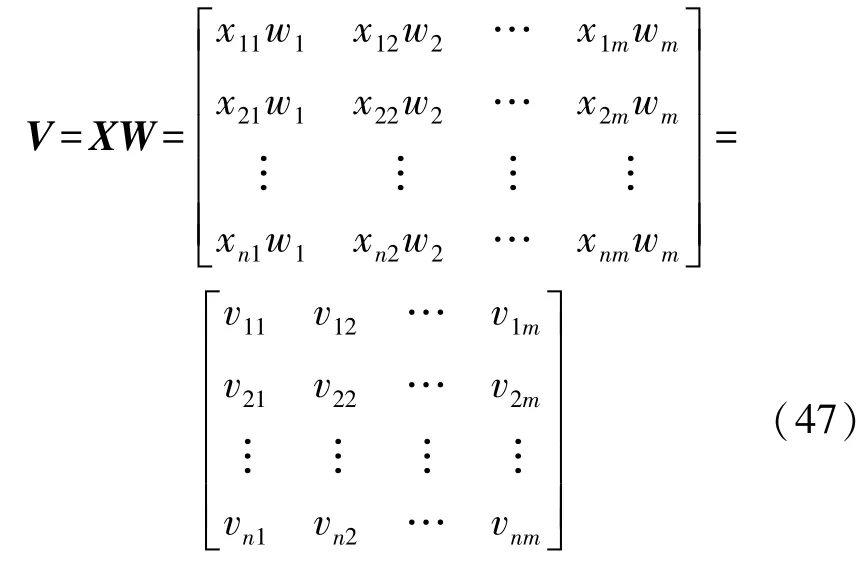
步骤2 计算正负理想解

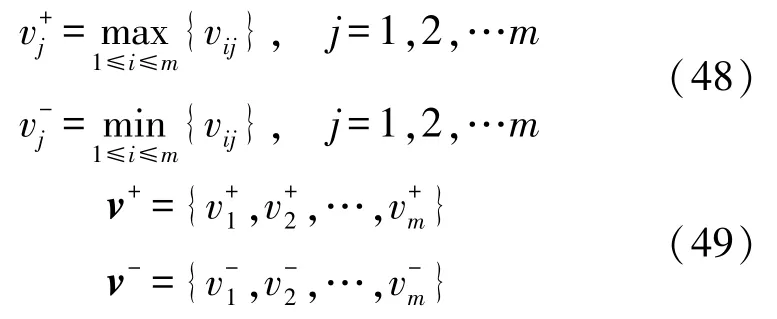
步骤3 计算欧氏距离

分别计算各个候选父节点与正负理想解的欧氏距离，如式(50)所示。基于欧几里得距离测量各个候选父节点的评价标准与正负理想解的距离。其中，是第i个候选父节点与正理想解的距离，是第i个候选父节点与负理想解的距离。

步骤4 计算各个候选父节点的相对贴近度

计算各个候选父节点的相对贴近度，如式(51)所示，Ci表示第i个候选父节点的相对贴合度。该数值反映了评估的候选父节点与正理想解的贴近程度以及与负理想解的远离程度。

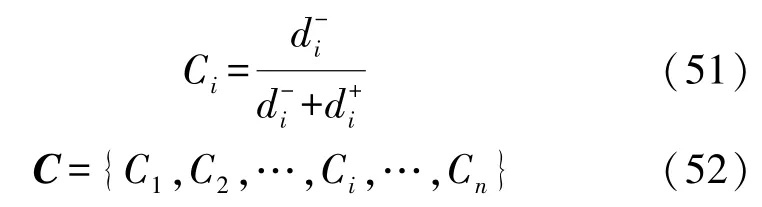
步骤5 降序排列相对贴近度的值

Ci的值越大，表明该方案与正理想解的距离越近，即候选父节点i与最优的理想下一跳节点越接近，综合评价结果越好。因此，将式(52)中计算出的各个候选父节点对应的相对贴近度的值降序排列，贴近度最大值对应的候选父节点为最优的下一跳节点。

3 仿真实验及结果分析

本文将MRM-CT和目前较典型的ETXOF(以ETX为路由度量)、0.8ETX＋0.2REI[2](多路由度量评估方法中依据主观经验确定各路由度量的权重系数，且性能相对较好的一种)和OF-FL[27](采用模糊逻辑的方法评估多个路由度量的一种方法)、等算法通过OPNET14.5仿真软件平台定量对比分析。

3.1 实验参数设置

节点随机分布在500 m×500 m的网络场景中。数据分组的到达服从泊松分布。节点的初始能量为0.75 J~1.00 J之间的随机值。当节点的剩余能量小于其初始能量的5%时，认为节点死亡。其他参数见表2。

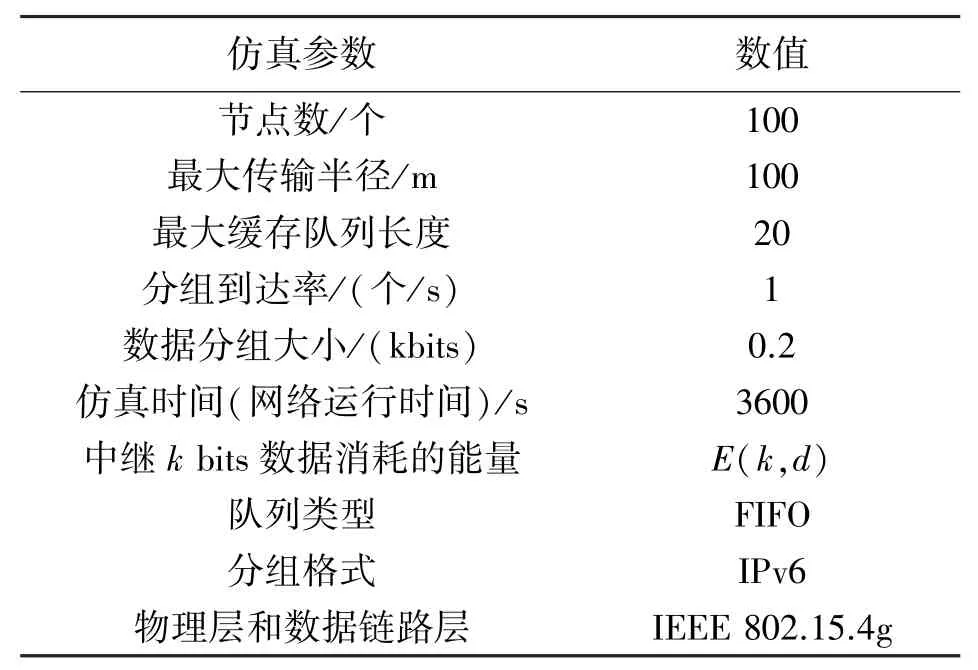
表2 实验参数设置

表2中E(k，d)可由式(53)计算得出。

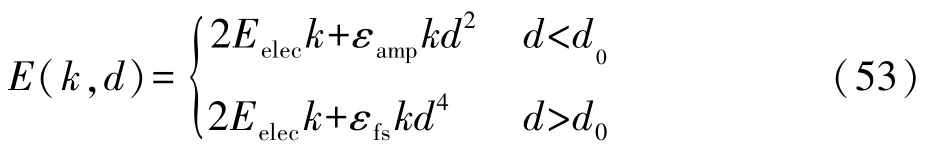
式(13)中的相关参数如表3所示[28]。

表3 E(k，d)参数

3.2 实验结果分析

①平均分组投递成功率

图2显示了MRM-CT、ETXOF、0.8ETX＋0.2REI和OF-FL的平均分组投递成功率。可见在网络运行初始阶段各算法的分组投递成功率还不稳定，2 400 s后逐渐达到稳定状态。且MRM-CT的平均分组投递成功率明显优于ETXOF、0.8ETX＋0.2REI和OF-FL的。通过提出采用递归的方法评估了候选父节点的剩余能量指数和缓存占用率，并采用和值、均值和均方差的方法评估候选父节点与目的节点间各链路所需的ETX和时延；采用组合赋权法确定目标函数中路由度量的权重；采用TOPSIS法确定偏好父节点等机制；MRM-CT的分组投递成功率显著优于其他算法的。

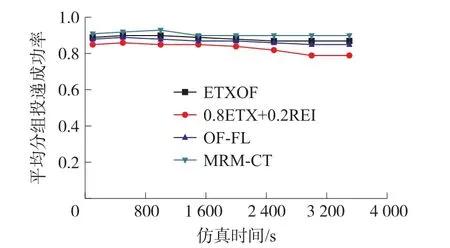
图2 平均分组投递成功率

②平均端到端时延

图3给出了MRM-CT、ETXOF、0.8ETX＋0.2REI和OF-FL的平均端到端时延。其中MRM-CT的端到端时延明显低于其他算法。MRM-CT提出采用和值、均值和均方差的方法评估候选父节点到目的节点间各链路所需的时延；提出采用组合赋权法综合主、客观赋权法得到的权重；并依据TOPSIS法确定偏好父节点，从而选择最优路径传输数据。因而MRM-CT可明显改善端到端时延。

图3 平均端到端时延

③平均存活节点数

网络中平均存活的节点数量可以反映网络的能耗情况。平均存活节点数越多，则表明网络能耗越小，反之亦然。图4给出了MRM-CT、ETXOF、0.8ETX＋0.2REI和OF-FL在网络运行过程中存活的平均节点数量。可见在不同时刻，MRM-CT的平均存活节点数均明显优于ETXOF、0.8ETX＋0.2REI和OF-FL的。因此，MRM-CT可显著降低能耗，节约网络资源，延长网络寿命。

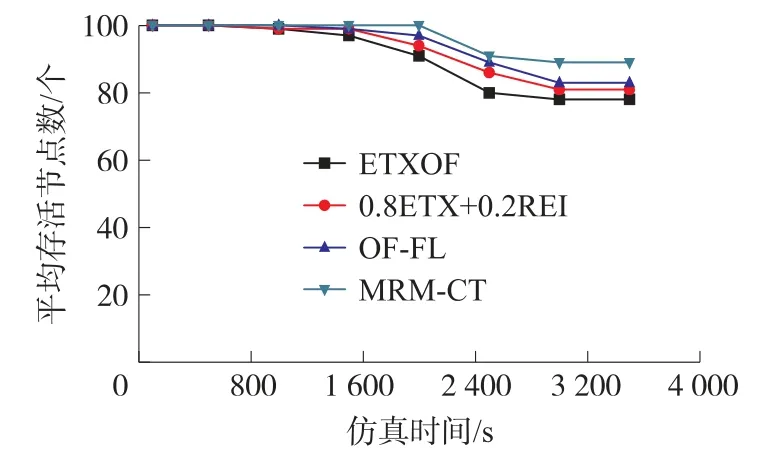
图4 平均存活节点数

④偏好父节点平均变更次数

偏好父节点的平均变更次数反映网络拓扑的稳定性，可用于调和网络性能和网络拓扑的稳定性。图5显示了MRM-CT、ETXOF、0.8ETX＋0.2REI和OF-FL的偏好父节点的平均变更次数。可见在网络运行初始阶段，各算法为构建网络拓扑，它们的偏好父节点变更次数较大，2 400 s后逐渐达到稳定状态。且MRM-CT的偏好父节点变更次数均低于ETXOF、0.8ETX＋0.2REI和OF-FL的。因此，MRMCT可在保障网络拓扑稳定的前提下，有效的改善网络在时延、网络寿命等各方面的性能。

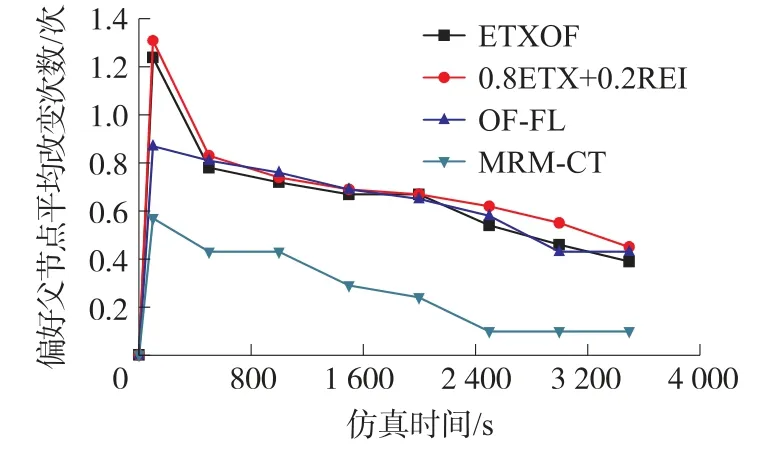
图5 偏好父节点的平均更换次数

⑤权重系数

图6给出了在网络运行过程中部分节点的权重系数变化曲线。本文随机选择了节点6(对应图6(a))、节点38(对应图6(b))、节点54(对应图6(c))和节点92(对应图6(d))的权重系数变化规律。由此可知，MRM-CT可根据网络的实际运行情况及用户、控制中心等部分人为因素动态调整各个路由度量的权重系数。

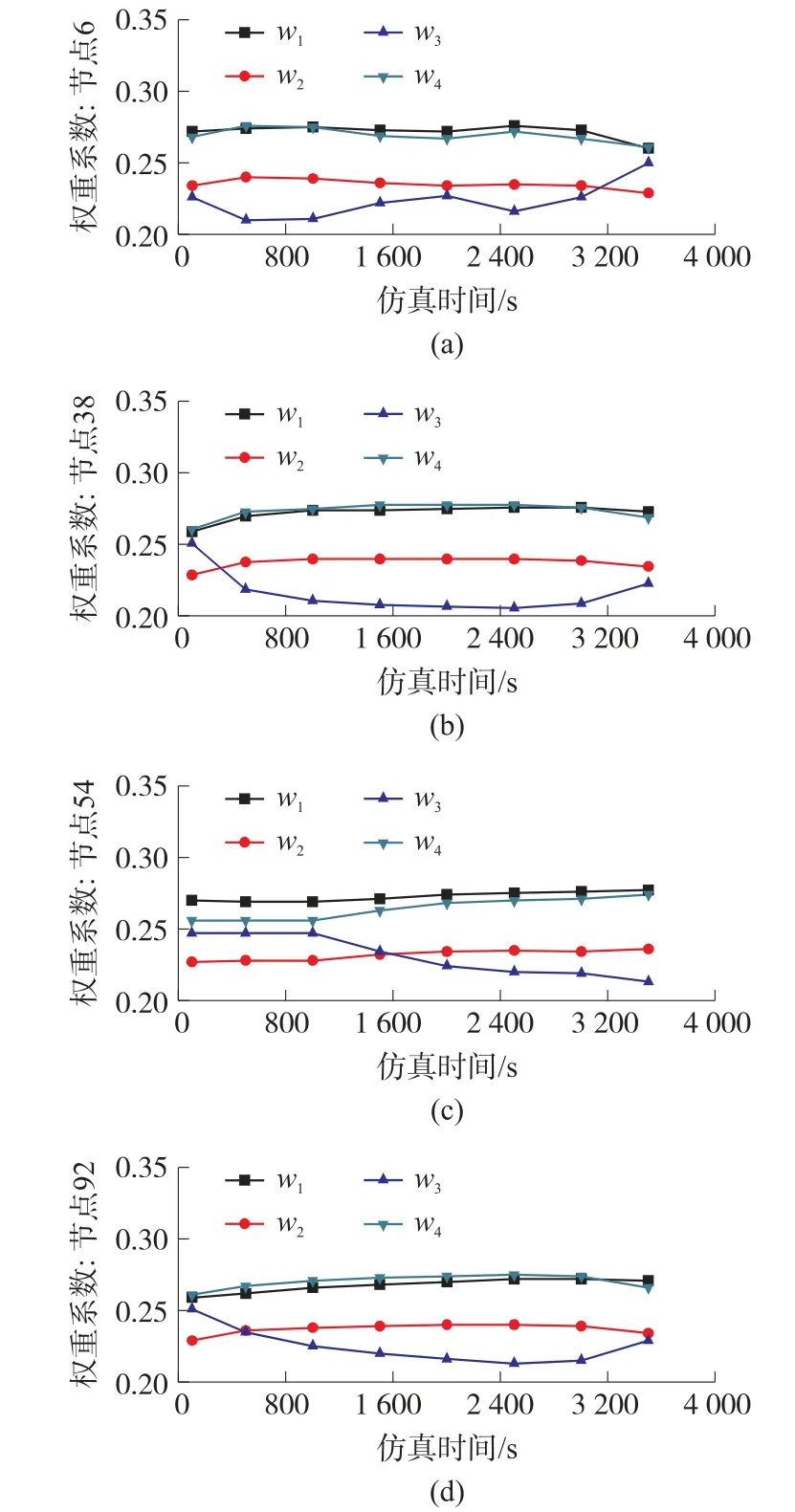
图6 部分节点权重系数展示

4 结束语

本文针对现有RPL及其相关改进算法在多路由度量评估中存在的问题，提出MRM-CT算法。该算法提出新的复合目标函数，提出采用组合赋权法确定复合目标函数中各路由度量的权重系数，提出采用TOPSIS法确定下一跳节点等机制。并通过仿真实验和理论分析证明MRM-CT可显著降低时延，提高分组投递成功率等，明显优于RPL及其现有相关改进算法。在未来的工作中，拟通过研究机器学习、6G等技术与低功耗有损网络路由协议相结合，进一步优化网络性能，满足应用需求。