基于EMD(经验模态分解)奇异值熵的城市轨道交通直流牵引供电系统短路故障辨识*
何 亮 吴 浩 李思文 张扬鑫 崔洪敏 刘 炜
(1.四川轻化工大学自动化与信息工程学院,644002,自贡;2.成都地铁运营有限公司,610058;3.西南交通大学电气工程学院,610031,成都∥第一作者,助理工程师)
直流牵引供电系统作为城市轨道交通运营的动力源泉,其安全运行是保障乘客人身安全和列车正常运行的基础[1]。现有的直流牵引供电系统保护以DDL(电流变化率和电流增量)保护、双边连跳保护[2]为主。随着运行线路的延伸、高峰时段列车发车密度的增大,以及城郊与城际供电距离过长等情况的不断出现,现有的保护对远端短路电流和充电电流区分能力较弱。文献[3-6]基于Matlab/Simulink软件建立直流牵引供电仿真模型,仿真分析了列车启动电流和远端短路电流的特点,为故障辨识提供了理论依据。文献[7-8]利用Matlab/Simulink软件中S-Function建立钢轨集肤效应模型,通过对比Mexh小波变换提取的远端短路电流和充电电流时间常数的大小来辨识故障。文献[9]利用ILMD(改进局部均值分解)分解馈线电流,再计算各频段的时频熵,通过比较其大小识别故障。文献[10]将电流积分值、积分时间内电流平均值和最大值的比值分别与保护整定值对比,可有效避免保护误动作。上述方法在直流牵引供电系统故障辨识中取得了一定的效果,但基于小波分解信号需要选择合适的小波基及分解层数,缺乏自适应性;基于电流积分和比值的方法需要计算短路后1 s的所有数据(采样率越高,1 s所采的点越多),计算量大。
近年来,EMD(经验模态分解)及SVD(奇异值分解)理论在电力系统故障、轴承故障等方面的辨识得到较为成熟的应用[11-15]。文献[12]采用核主元分析提取EMD熵值(能量熵和奇异值熵)的融合特征,再通过支持向量机进行滚动轴承故障诊断。在直流牵引供电领域,文献[16]基于EMD和能量权重构建多尺度特征熵,获取特征矢量进而有效地区分牵引网振荡电流和故障电流。但此方法选取保护启动前200 ms的电流数据,具有一定的后延性。
借鉴上述研究,考虑直流牵引供电系统远端电路和机车充电电流信号复杂程度不同,本文将EMD奇异值熵应用到城市轨道交通直流牵引供电系统短路故障辨识中。首先提取DDL保护启动后40 ms的远端短路和充电电流数据,再利用EMD分解电流信号得到特征向量矩阵,基于奇异值分解和信息熵理论构建奇异值熵,将该熵值大小作为远端短路电流和充电电流的判据。算例分析表明,该方法可应用于直流牵引供电系统远端短路和列车充电电流识别。
1 直流牵引供电系统远端短路电流及列车充电电流
城市轨道交通直流牵引供电系统主要由牵引变电所、列车、接触网、钢轨等组成,如图1所示。

图1 直流牵引供电系统远端短路和列车充电仿真示意图
钢轨作为直流牵引供电系统回流的载体,“工”字型的不规则横截面,使得钢轨具有非线性的铁磁特性,易受集肤效应的影响。当牵引供电系统发生金属性短路时,电流暂态信号中存在较大的频率变化,因此,需要考虑集肤效应对钢轨电阻的影响[17]。然而列车负载远大于钢轨阻抗,在列车起动过程中可忽略钢轨集肤效应的影响[18]。本文采用文献[8]提出的阶跃级数逼近法,利用S-Function软件建立钢轨模型,基于Matlab/Simulink软件搭建如图1所示的直流牵引供电系统模仿真型。仿真的远端短路电流数据与武汉地铁某牵引变电所提供的实测远端短路电流数据如图2所示。

图2 牵引变电所实测电流与仿真电流对比图
当列车行驶过整流牵引所站台附近的过分段,必然会有一个充电过程。过分段的段间距越长,产生的瞬时充电电流就越大,易造成保护误动作[18]。本文基于上述仿真模型在整流牵引所出口仿真列车充电电流,其仿真数据如图2所示。
1) 由图2可见,仿真短路电流由于受某些仿真条件的理想设置,与实测短路电流的差别较小,两者在幅值和变化趋势上几乎相同。
2) 为了定量描述仿真和实测短路电流数据的相似性,引入Kendall相关系数Tau-b[19]:

(1)
式中:
n——元素个数;
xi,yi——验证相似度x和y中的第i个元素;
ti,ui——分别为x和y中由相同元素组成的各个子集的元素数;
δ——函数自变量。
(1) 计算得到图2中实测短路电流和仿真短路电流之间的Kendall相关系数Tau-b=0.997 2。计算结果表明两者具有极高的相似度。
(2) 仿真和实测的列车充电电流均在较短的时间内快速上升到3 000 A左右。计算得到图2中实测和仿真的列车充电电流之间的Kendall相关系数Tau-b=0.783 2。计算结果表明两者具有较高的相似度。
(3) 对比图2中的远端短路电流和列车充电电流,可清楚发现:两者均按指数规律急剧上升,且初始时刻电流增量均大于40 A/ms;随着时间的推移,远端短路电流增量逐渐小于充电电流增量;在一定的时间内,充电电流幅值大于远端短路电流,故可能引起DDL保护误动作。
基于上述分析可知,本文所搭建仿真模型能近似仿真实际的远端短路和机车充电过程。这充分证明了所建模型的正确性。
在列车起动时,列车充电电流在电流增量和幅值方面与远端短路电流差别不大。远端短路时需要考虑钢轨集肤效应的影响,列车起动过程可忽略此影响,因此,两者电流在时频成分上具有较大的差异。下文将引入EMD奇异值熵定量分析电流信号的时频成分及复杂度,从而更加精准地辨识远端短路电流和列车充电电流。
2 EMD奇异值熵构成原理
2.1 EMD方法及特征向量矩阵
为分析处理非线性非平稳信号,文献[20]提出自适应信号时频处理方法——EMD。EMD依据信号自身的时间尺度特征,将信号中不同尺度的波动或趋势逐级剥离出来,生成一系列的IMF(本征模态函数)分量。每一个IMF分量均包含原始采集电流信号的本质特征,反映出信号中突变信息。原始采集电流信号f(t)经EMD处理后可表示为:
(2)
式中:
ci(t)——EMD分解后的第i个IMF分量,表征原始信号中从高频到低频不同频段成分;
n——IMF分量的数量;
r——残余分量,表征原始信号f(t)的平均趋势。
利用EMD分解原始信号,生成n个IMF分量(c1,c2,…,cn)和一个残余分量r。为了体现原始信号全部特征,定义EMD特征向量矩阵S,则:
S=[c1c2…cnr]T
(3)
2.2 SVD理论及奇异值熵
特征向量矩阵S是对原始信号时频域的一种划分,为了详细地反映信号中波动的差异,从数学矩阵的角度分析,提取特征向量矩阵S的奇异值。根据SVD理论可得:
S=UΛVT
(4)
式中:
U,V——分别为(n+1)×(n+1)阶和m×m阶正交阵,m为每个IMF分量的数目;
Λ——对角矩阵,主对角元素λ1,λ2,…,λ(n+1)为矩阵S的奇异值,且λ1≥λ2≥…≥λ(n+1)≥0。
设gi和vi均分别为正交矩阵U和V的列向量,则式(4)可等效为:
(5)
式中:
λi——矩阵S第i个奇异值。
由式(5)可得,任意矩阵S可看做gi和viT作外积与奇异值λi的加权和,奇异值即为加权权重。奇异值越大,其特征信息也就越大[21-22]。
为了定量描述信号时频成分和复杂度,引入奇异值熵,则奇异值熵Y可定义为:
(6)
(7)
式中:
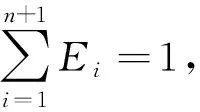
信号的复杂度与奇异值熵成正相关[23]。信号越复杂,其奇异值熵越大;相反,信号越单一,其熵值越小。
3 算例
3.1 仿真分析
采用前文建立的仿真模型,仿真远端短路和列车起动过程,以暂态电流为研究对象。在直流牵引供电系统中,一般设定直流断路器的保护延时时间为40 ms,因此本文取DDL保护启动后40 ms的远端短路电流和列车起动电流数据。考虑仿真和实测采样频率不一致,先对数据进行预处理,再进行EMD分解,其分解结果如图3和图4所示。

图4 列车充电电流EMD分解结果
由图3可知,远端短路电流经EMD分解后,得到4个IMF分量和残余分量r。各IMF分量幅值在初始一段时间的变化量最大,随后逐渐趋近于0,说明短路初始时刻,电流信号频率成分丰富。

图3 远端短路电流EMD分解结果
由图4可知,列车充电电流经EMD分解后,仅包含1个IMF分量c1与r。c1分量幅值小,且初始时刻c1分量幅值变化不大,随后其幅值变化越来越频繁,说明充电电流频率成分单一。
3.2 故障辨识判据
由图3和图4可知,在DDL保护启动后的一段时间内,远端短路电流信号复杂,包含的时频信息多。而在列车充电过程中,列车阻抗占主导地位,阻抗固定,其信号比较单一。而奇异值熵与电流信号的复杂度成正比例关系,即远端短路电流奇异值熵大,而充电电流奇异值熵小。通过计算两者电流信号的奇异值熵,分析其熵值的大小关系,设置判据门槛值Kset,从而辨识列车充电电流和远端短路电流。辨识算法流程图如图5所示。
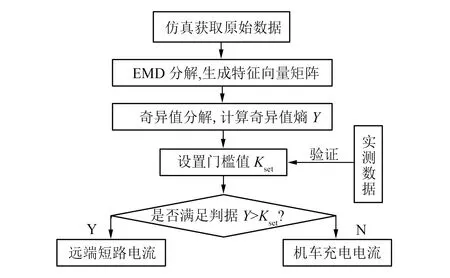
图5 基于EMD奇异值熵的直流牵引供电系统故障辨识算法流程图
为了定量描述两者信号的复杂度,利用式(3)—式(7)计算列车充电电流和远端短路电流各20组信号的奇异值熵,其结果如图6所示。

图6 仿真电流奇异值熵的柱状图
远端短路电流经EMD分解为4个IMF分量,而列车充电电流仅包含1个IMF分量。计算的充电电流EMD奇异值熵约为1.00×10-3,而远端短路电流EMD奇异值熵均大于1.00×10-2。考虑实际环境以及某些仿真条件理想化,辨识门槛值Kset设定为5.00×10-3。
3.3 实测验证
根据武汉地铁某牵引变电所提供的实测数据,组成20组实测远端短路电流数据和5组实测列车充电电流数据,分别计算两者的EMD奇异值熵,其结果如图7和表1所示。
在实际直流牵引供电系统中,各个短路点随机发生,列车运行状态以及牵引供电系统环境均可能不一样。因此,每个短路数据包含的时频信息可能不同,信号的复杂程度不同,其EMD奇异值熵也有所差别。在图7中,分析的20组数据EMD奇异值熵大小不一,但均大于辨识门槛值Kset。在表1中,分析的5组数据EMD奇异值熵均远小于Kset。实测和仿真数据表明,可根据电流信号EMD奇异值熵的大小来辨识远端短路电流和列车充电电流,且Kset设定的可靠合理。
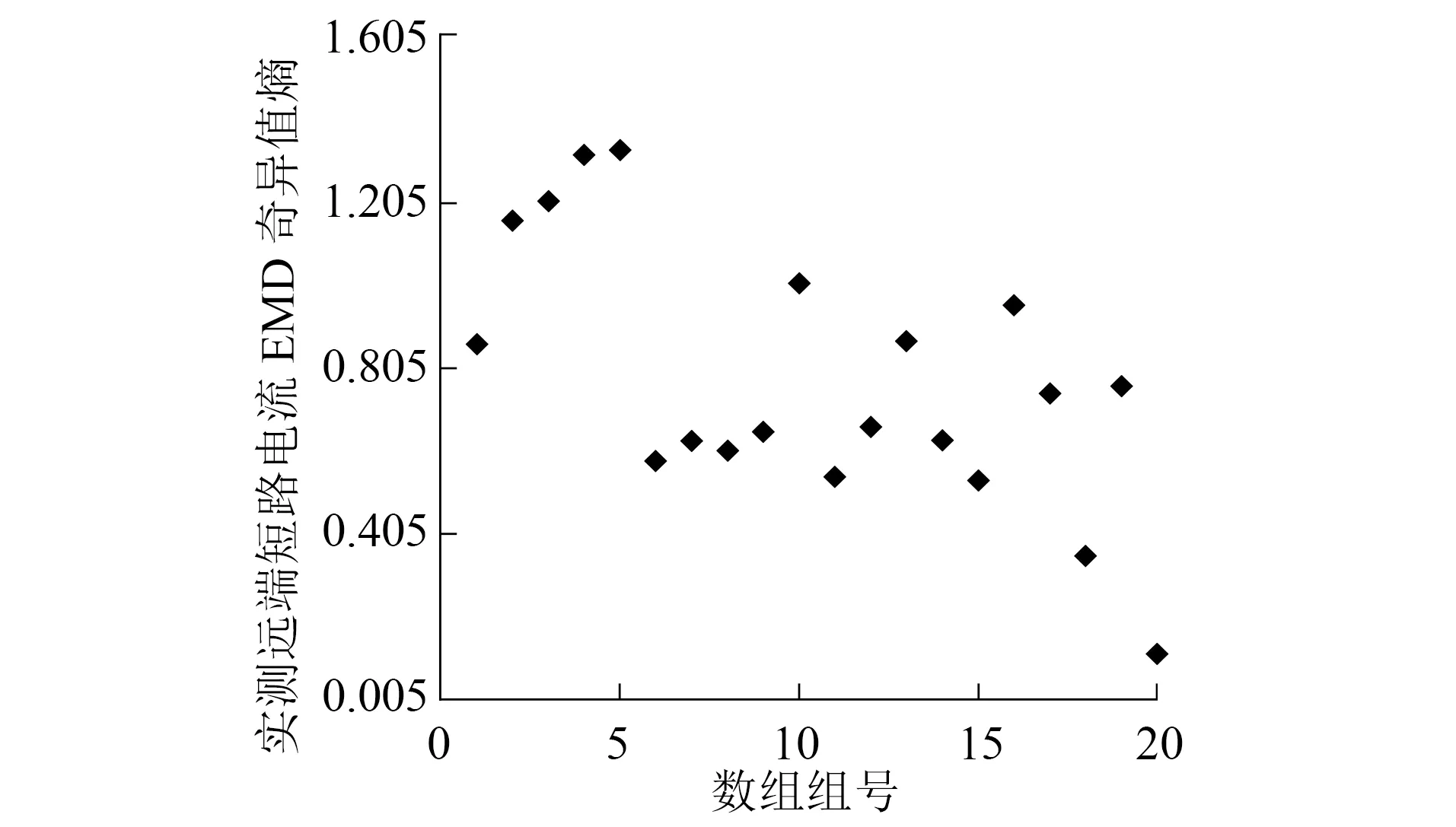
图7 实测远端短路电流奇异值熵散点图
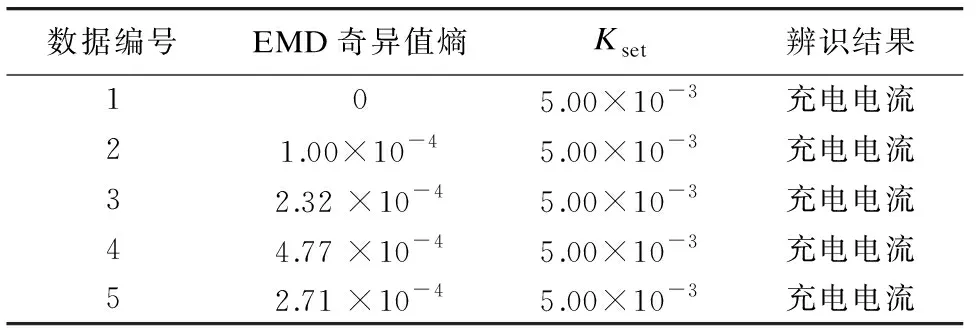
表1 实测列车充电电流EMD奇异值熵计算结果表
3.4 与小波奇异熵对比
小波变换在处理非平稳暂态信号方面具有一定的优势,同时小波奇异熵现已运用在电力系统故障辨识和城市轨道交通弓网燃弧电流扰动分析中[23-24]。因此,本文随机选择远端短路电流、列车充电电流仿真数据和远端短路电流实测数据各3组,计算其小波奇异熵和EMD奇异值熵,其结果如表2所示。

表2 小波奇异熵和EMD奇异值熵计算结果比对表
由表2可知,处理相同数据时,选择的小波基和分解层数不同,其结果不相同,而经EMD处理后其结果唯一。小波变换处理仿真数据时,远端短路电流熵值远大于列车充电电流熵值,当处理远端短路电流实测数据时,其大部分熵值小于列车充电仿真电流熵值,其辨识能力较弱;而使用EMD奇异值熵时,远端短路电流熵值均远大于列车充电电流熵值。因此,由于EMD具有较好的适用性,采用EMD奇异值熵可有效辨识故障。
4 结语
本文利用EMD准确提取电流信号中微小波动,将信号分解为从高到低不同频段成分,结合SVD理论和信息熵构造奇异值熵,分析信号复杂度,将其作为辨识特征量。仿真和实测数据表明,该方法可有效辨识远端短路电流和列车充电电流。主要结论如下:
1) 结合理论和仿真分析,当牵引供电系统发生远端短路时,其暂态电流包含的时频信息多,信号相对复杂,其奇异值熵大;而列车充电电流中的时频信息较少,信号相对简单,其熵值小。因此可根据不同的奇异值熵建立判据辨识故障。
2) 通过选择不同的小波基和分解层数,可计算信号的奇异值熵。EMD依据信号本身的时间尺度特征分解处理,具有较好的自适应性。分析两者处理结果,验证了本文方法的优越性。

