轨道交通车辆层状弹簧结构参数对其垂向刚度的影响*

陈清化 龙垚坤 程海涛 张 波

(1.湖南铁路科技职业技术学院，412006，株洲； 2.株洲时代新材料科技股份有限公司，412007，株洲；3.中车株洲电力机车有限公司，株洲 412001 ∥ 第一作者，讲师)

0 引言

近年来，随着轨道交通车辆需求的快速增长，各主机厂对车辆部件的交付进度、成本和质量都提出了新的要求。层状弹簧作为二系悬挂的重要减振部件，相较其它结构形式橡胶弹簧的受载变形小、制造工艺复杂，其垂向刚度特性对车辆无气动力学的影响显著。层状弹簧因其垂向变形小、所需安装空间小等优点在地铁及磁浮车辆上有较广泛应用。研究层状弹簧结构参数对其性能的影响规律对于层状弹簧的设计开发、结构优化以及质量保证具有积极的促进作用。

目前，国内外关于层状弹簧的研究成果较少，有部分学者进行过相关的研究工作。文献[1]运用超弹性模型计算橡胶弹性元件的静态特性，确定了有限元仿真计算在橡胶弹簧刚度性能计算中的可行性和优越性。文献[2]采用Mooney Rivlin本构模型金属橡胶件的静态刚度进行了大量的有限元分析计算，研究确定了材料系数对于金属橡胶件静态刚度计算影响规律。文献[3]研究介绍锥形弹簧作为一系弹簧应用的技术特点及其在轻轨车辆中使用情况。文献[4]研究半沙漏式辅助弹簧的橡胶胶层厚度及受载方式对该产品在低温下的刚度性能恢复能力有重要影响。文献[5]进行了一系列橡胶弹簧关于橡胶的疲劳研究工作，并提出多种影响橡胶疲劳损伤的参量。文献[6]针对叠层橡胶弹簧失稳问题，研究通过优化结构参数减小横向偏移量，提高了叠层橡胶弹簧垂向稳定性。文献[7]采用理论推导、仿真分析及试验验证研究分析了橡胶弹簧的隔振特性与激励频率、隔振系统质量、橡胶弹簧刚度和阻尼之间的关系。文献[8]研究得出了轴箱层叠橡胶弹簧刚度随温度的变化情况。文献[9]研究得出非线性橡胶弹簧减振系统的数值分析及设计方法能够准确设计非线性减振系统的动力学特征。文献[10]研究了低温和频率对于橡胶弹簧元件刚度的影响。目前学者们的研究均没有涉及层状弹簧结构参数对垂向刚度性能影响方面。

目前，层状弹簧的设计开发主要采用借鉴参考类似产品的结构和有限元仿真分析方式进行，对于结构参数与其性能的相关性并未有相关的研究成果，不清楚层状弹簧各结构参数对于其刚度性能的影响规律。层状弹簧一次开发命中率不高，而时间和人力成本较高。为能够准确、高效服务轨道交通车辆产业发展，针对层状弹簧结构参数与垂向刚度性能相关规律进行研究，同时也为其它类似橡胶产品的设计开发及改进优化提供参考。

1 基于关键结构参数的层状弹簧性能定性分析

层状弹簧结构主要由金属和橡胶硫化而成(见图1)，提供承载和辅助减振作用，在空气弹簧无气时，起主要承载和减振作用。

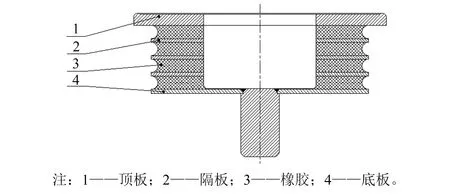
图1 层状弹簧结构示意图

层状弹簧主要靠橡胶的变形来实现减振功能，其性能特性主要由橡胶材料特性、结构设计及生产工艺决定，其中结构参数设计的影响较为关键。层状弹簧主要结构参数如图2所示。

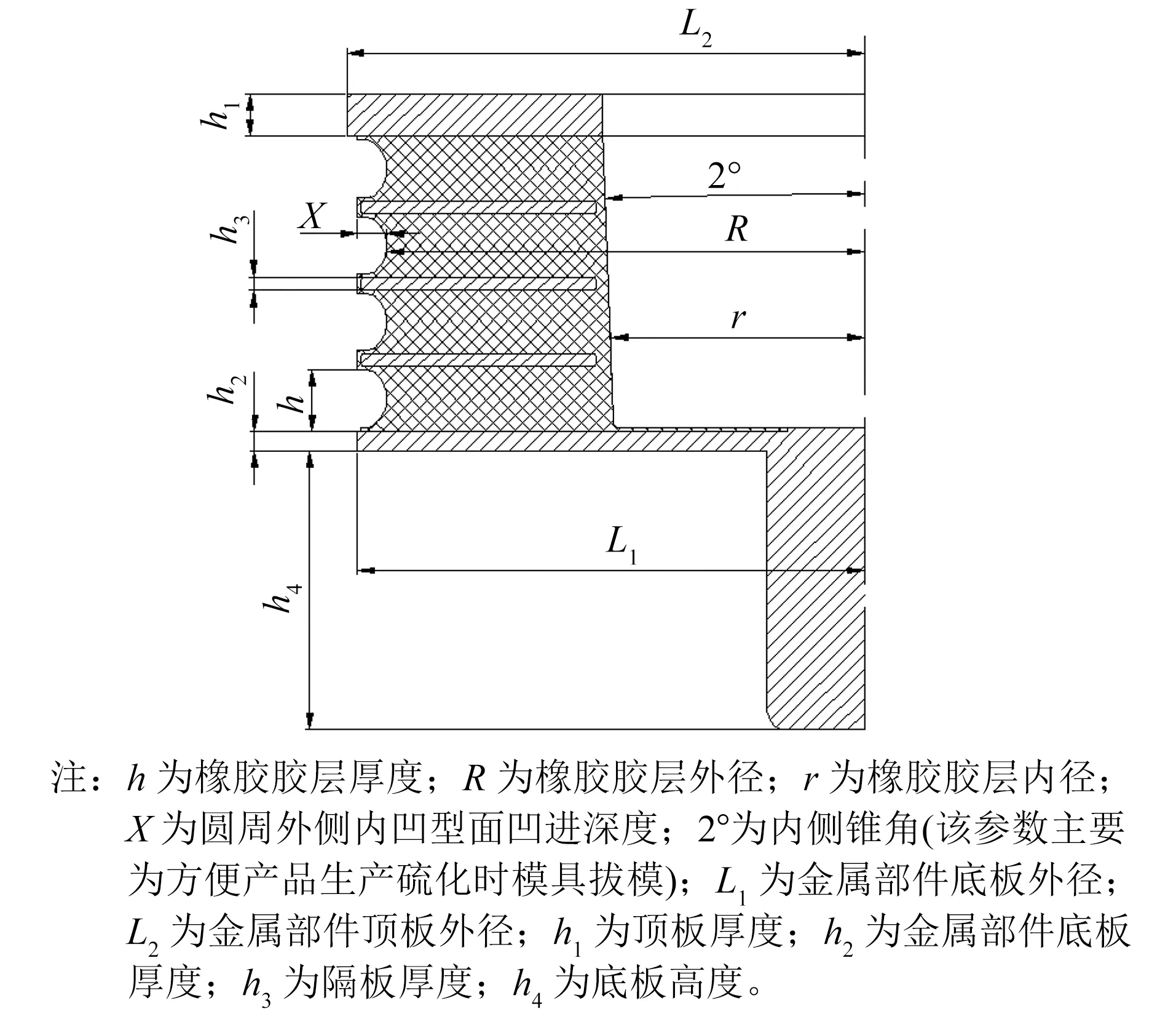
图2 层状弹簧结构参数示意图

为研究结构参数对层状弹簧垂向刚度性能的影响，考虑变更层状弹簧结构参数的多样性、复杂性以及高昂的采购和试制成本，利用有限元仿真分析和试验相结合的方法研究结构参数对于层状弹簧垂向刚度特性的影响规律。

首先，通过对随机样品一(四层橡胶结构层状弹簧)进行垂向加载试验；然后，利用有限元软件Abaqus6.14进行仿真分析，计算模型采用轴对称模型，载荷与边界条件如图3所示。固定模型的底板底面，模拟车辆真实加载情况。在顶板的顶面施加垂下压力(转化为位移加载)。橡胶网格采用CAX4H单元，其他金属部件网格均采用CAX4R单元，网格模型如图4所示。模型垂向加载计算结果如图5～7所示。通过比较仿真结果与试验结果的差异，修正仿真计算过程中橡胶材料参数，降低有限元仿真分析的误差，减小橡胶材料参数和仿真分析方法对于后续验证的影响。

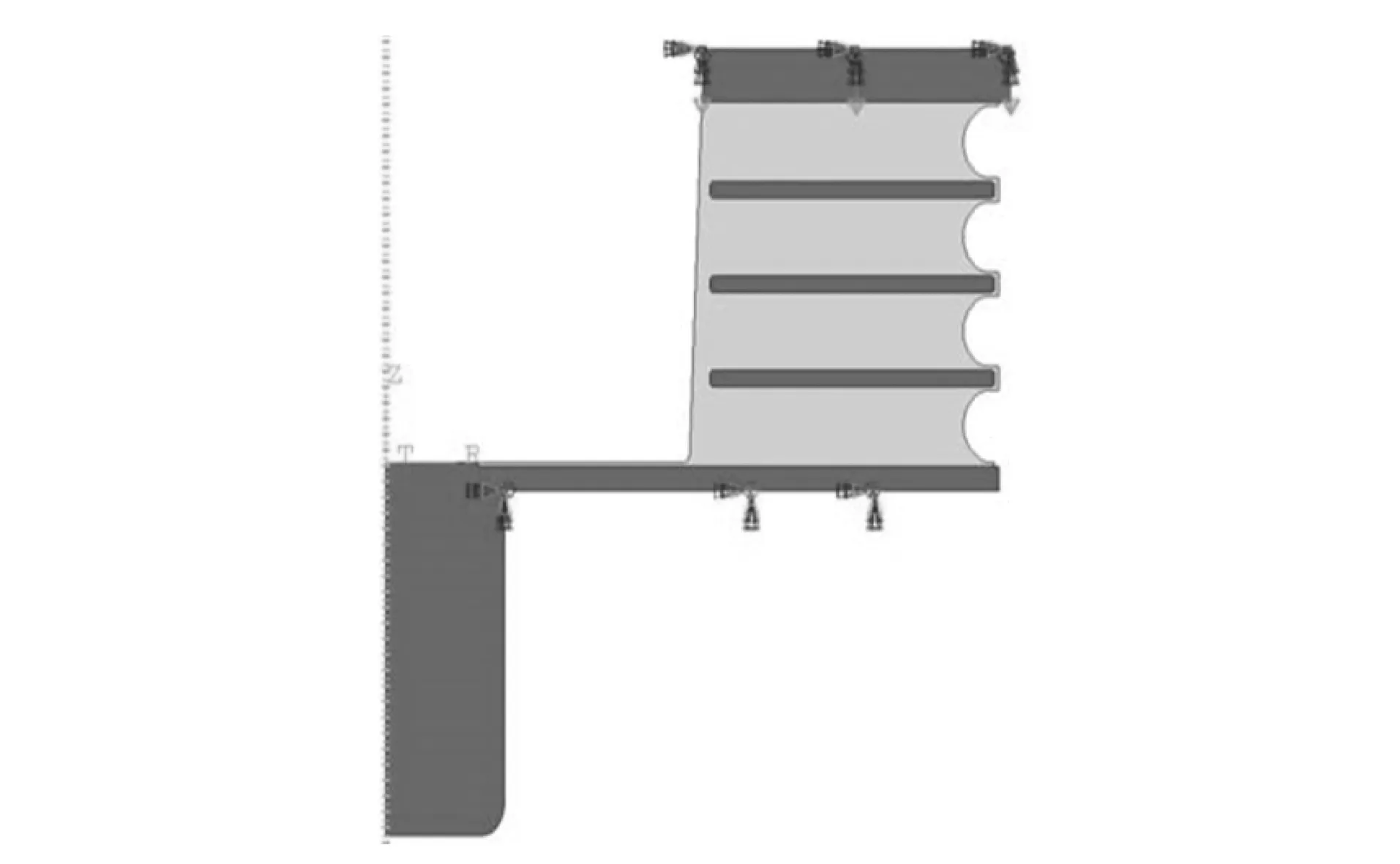
图3 四层橡胶结构层状弹簧载荷与边界条件

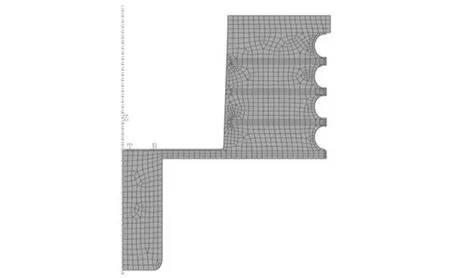
图4 四层橡胶结构层状弹簧有限元网格

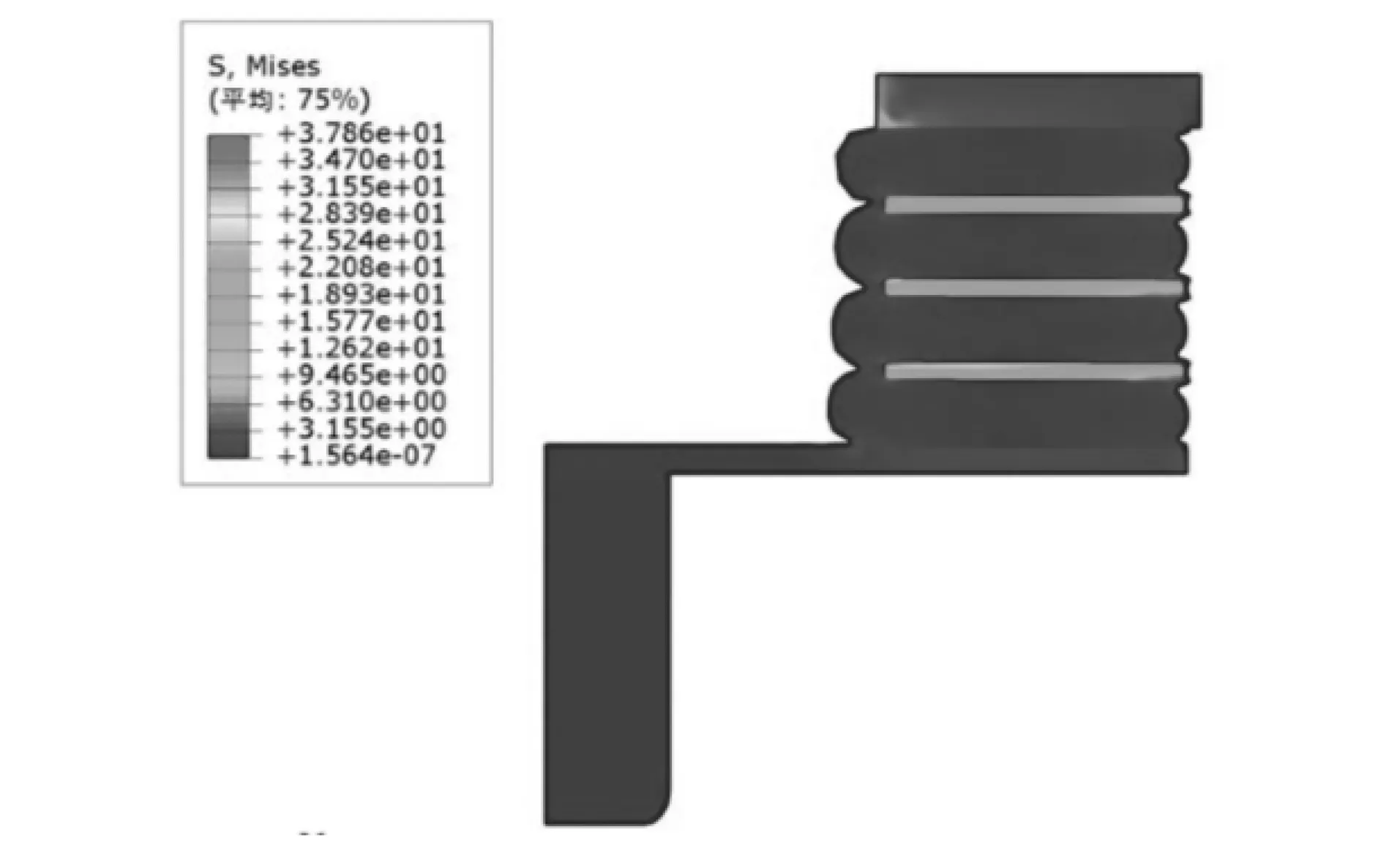
图5 四层橡胶结构层状弹簧模型的Mises应力云图

利用有限元仿真分析方法对多种结构层状弹簧金属部件结构参数的单独变化进行仿真分析。结果显示金属部件尺寸变化对于其垂向刚度性能几乎无影响，而橡胶参数变化则导致其垂向刚度性能产生波动。由此可以确定，橡胶参数为影响层状弹簧垂向刚度性能的关键结构参数。下文主要对关键结构参数变化对层状弹簧垂向刚度性能的影响进行研究。

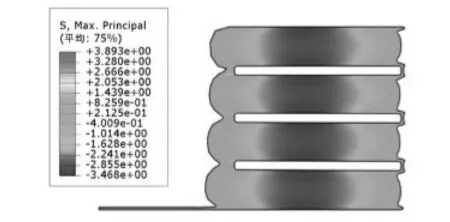
图6 四层橡胶结构层状弹簧橡胶层主应力云图

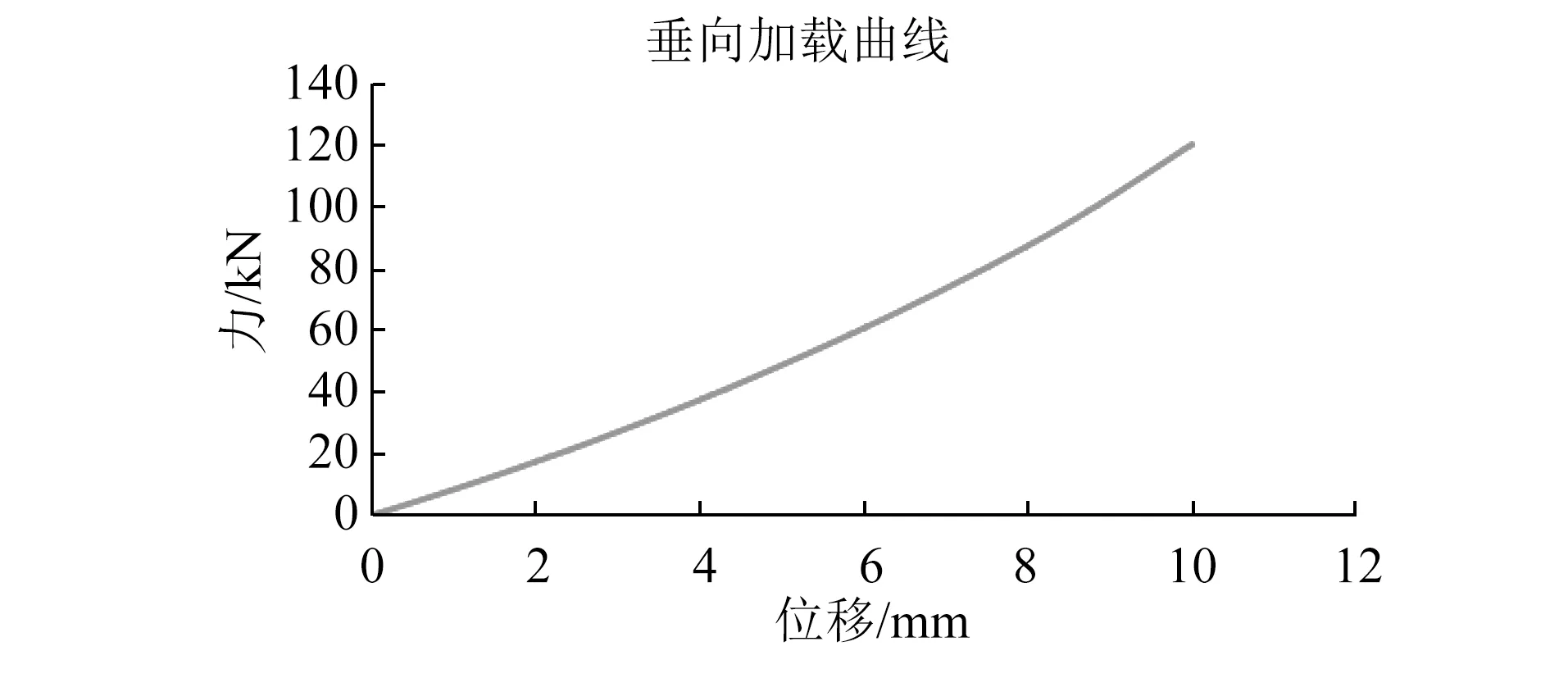
图7 四层橡胶结构层状弹簧模型垂向加载曲线

对4层橡胶结构(样品一)和3层橡胶结构(样品二)这2种典型层状弹簧样品的结构参数的变化进行研究。因辅助弹簧承载的载荷较大，同时考虑橡胶的散热性差等因素，轨道交通车辆用层状弹簧的胶层一般设计为多层橡胶，并通过金属隔板(隔板通常选用65Mn材料，顶板和底板材料通常选用Q235B)隔开的方式，避免出现单层橡胶很厚的情况。考虑产品的疲劳寿命和耐环境影响，橡胶胶层采用等应变设计。各层橡胶胶层厚度一致，橡胶材料(胶料硬度为55 Shore A)通常添加多种成分。初始设计参数如表1所示。在初始参数基础上改变两种样品橡胶的结构参数，变化范围为0～10%，变化步长为2%。

表1 两种层状弹簧样品的橡胶胶层基本参数表

针对样品一和样品二的胶层厚度h变化、胶层外径R变化和胶层内径r变化，利用有限元仿真分析计算得到多组不同变化参数对应产品垂向刚度值。然后利用公式(1)分别计算出不同结构层状弹簧垂向刚度基于各结构参数的相对灵敏度值。

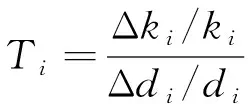
(1)

式中：

di——第i个结构设计参数；

Δdi——第i个结构参数的变化值；

ki——第i个参数对应的垂向刚度值；

Δki——第i个参数变化后对应的垂向刚度变化值。

两种层状弹簧样品的结构参数灵敏度计算结果如图8～9所示。

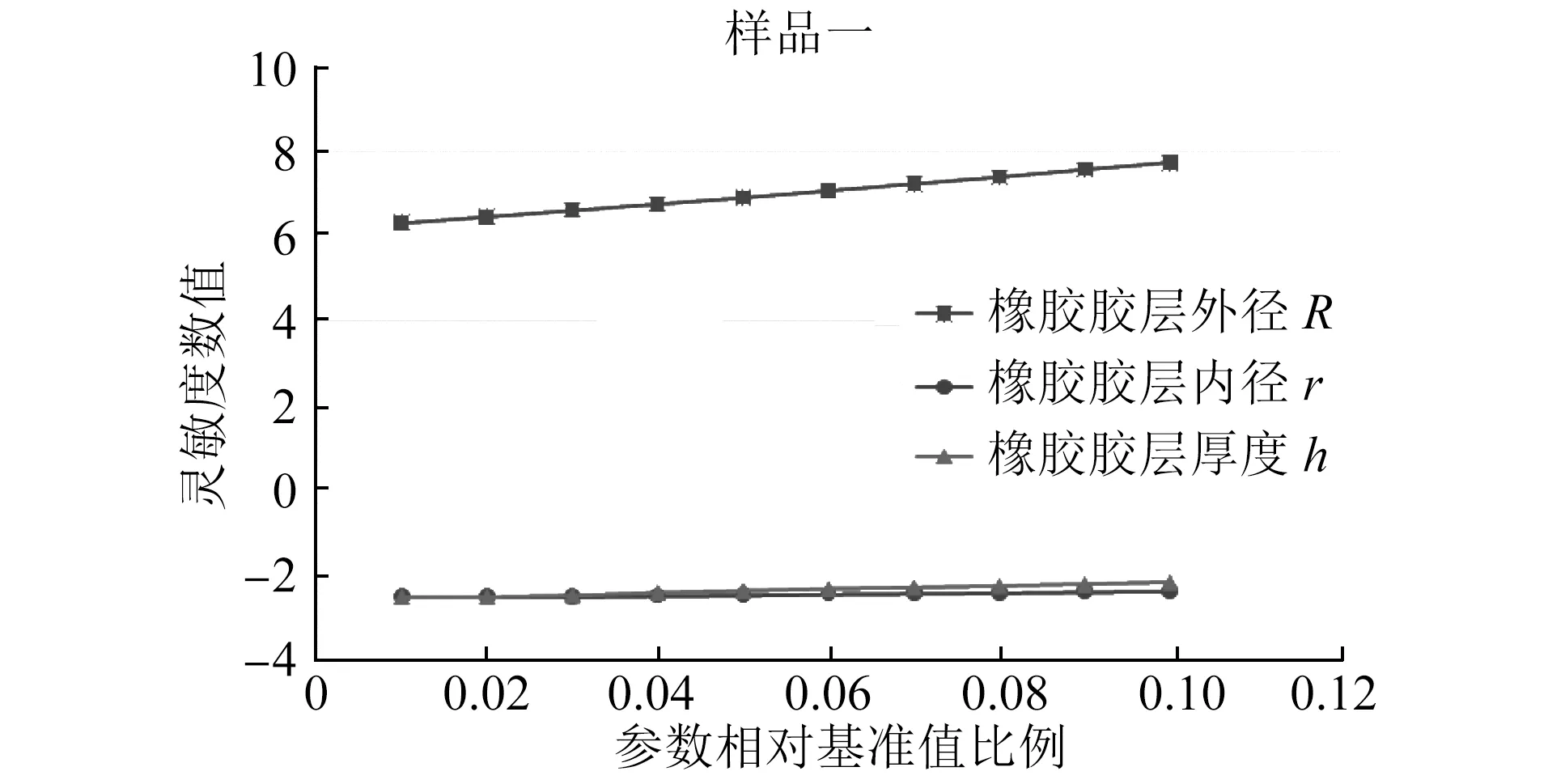
图8 层状弹簧样品一各结构参数灵敏度分析图

两种不同结构不同胶层数量的层状弹簧结构参数变化率对应的垂向刚度变化率结果虽不完全相等，但所呈现的变化趋势一样。增大R，层状弹簧对应的垂向刚度会增大，此为正向影响，影响的灵敏度值约为5.5～7.7，影响程度较大；增大r，层状弹簧对应的垂向刚度会减小，此为负向影响，影响的灵敏度值约-1.7～-2.5，影响程度较为明显；增大h，层状弹簧对应的垂向刚度会减小，此为负向影响，影响的灵敏度值约-2.1～-2.5，影响程度较为明显。

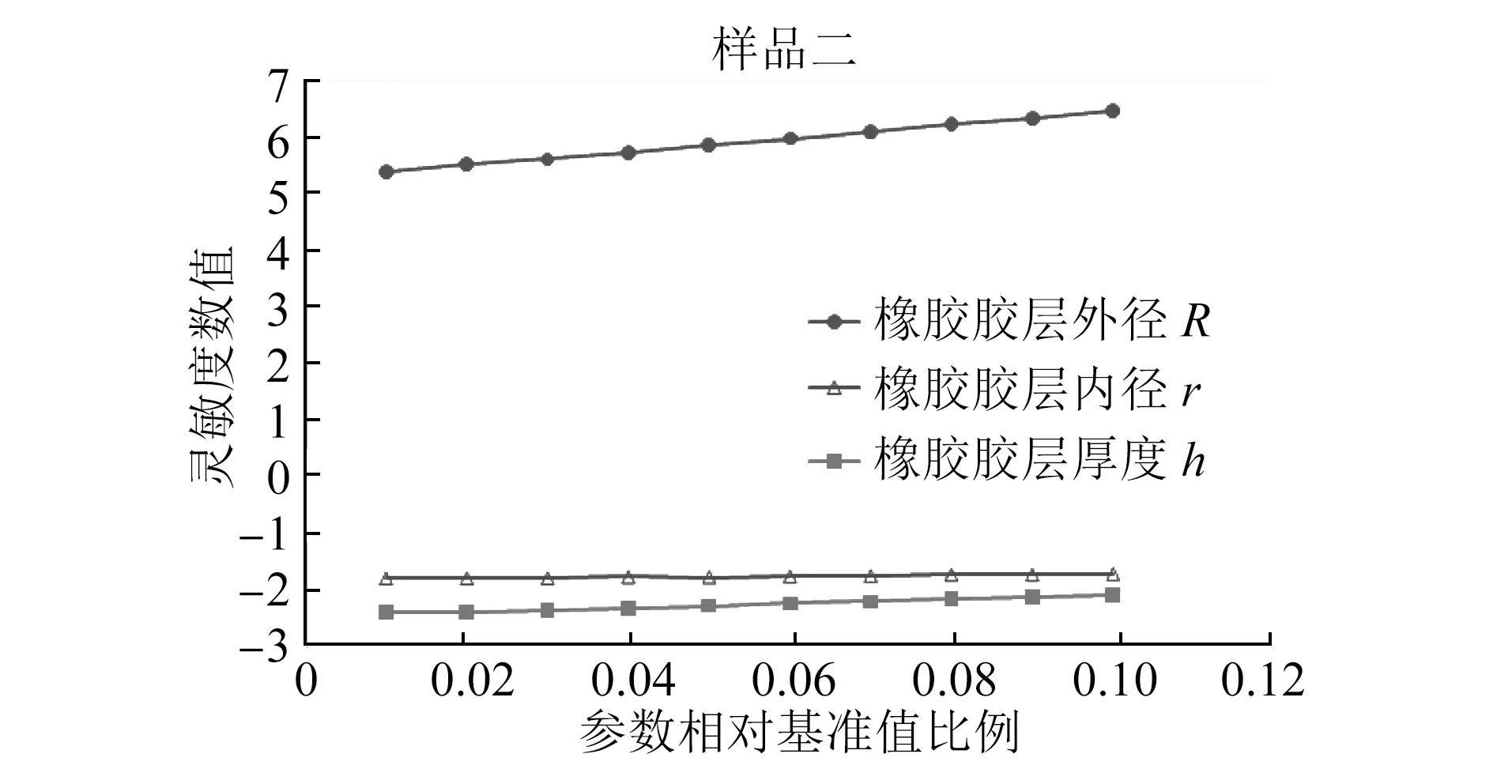
图9 层状弹簧样样品二各结构参数灵敏度分析图

样品一和样品二的胶层厚度、胶层内径、胶层外径均不变的情况下，改变胶层层数n，通过有限元仿真可得样品垂向刚度K随n的变化趋势如图10所示。

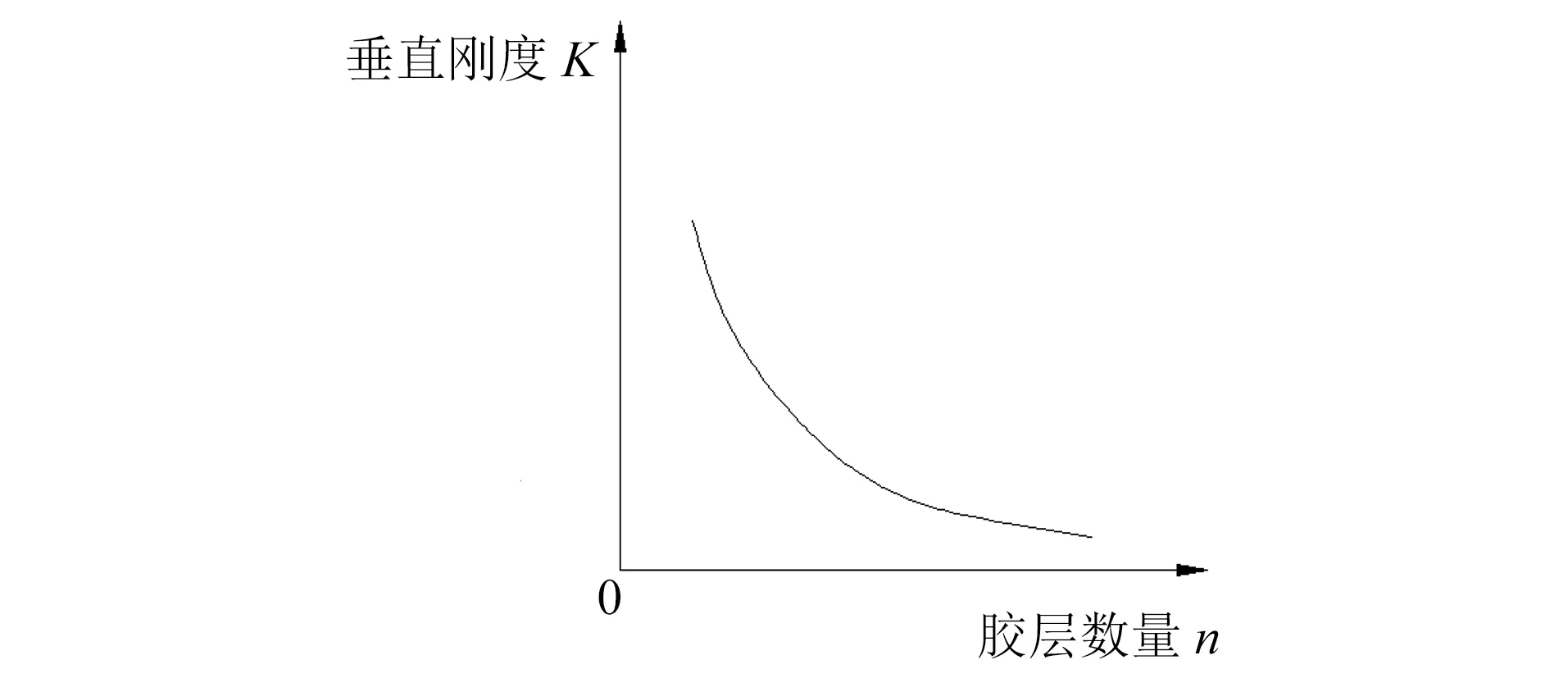
图10 层状弹簧垂向刚度与胶层数量关系图

综上所得：层状弹簧的结构参数R、r、h、n为影响层状弹簧垂向刚度性能的关键结构参数。这些参数对层状弹簧的垂向刚度有较为明显的影响，其中参数R对垂向刚度的影响程度最大。

2 基于关键结构参数的层状弹簧性能定量分析

上述研究得到了关键结构参数对于层状弹簧性能定性影响规律，为更好指导层状弹簧的设计和优化，需研究层状弹簧关键结构参数对其性能的定量影响规律。层状弹簧的使用环境较为复杂，橡胶材料中需要添加耐环境作用的特殊原料。通过调整橡胶材料的成分含量改变橡胶的硬度，而橡胶材料的硬度特性与橡胶的弹性模量E存在一定的复杂非线性关系。针对橡胶材料硬度的变化，最终都可用E值来进行反映。Gent在1981年基于橡胶的不可压缩性特征提出过橡胶隔震支座竖向刚度计算理论，文献[11]对该理论进行了简化，简化公式为：

K=EcbA/h

(2)

式中：

K——垂向刚度；

A——受载截面面积；

Ecb为——修正弹性模量，其数值主要与橡胶弹性模量E相关。

而层状弹簧与橡胶隔振支座存在结构和功能上的差异，橡胶的配方及性能要求也不相同。层状弹簧橡胶的修正弹性模量与橡胶弹性的关系为：

Ecb=μE

(3)

μ与橡胶块受载面积和自由面积比值等参数有关，其关系式为：

μ=1+mS2

(4)

式中：

S——单层橡胶面积比，计算公式如公式(5)；

m——与橡胶形状和橡胶截面有关的修正参数。

S=(R-r)/2h

(5)

在进行轨道交通车辆用层状弹簧橡胶的厚度设计时，考虑到散热要求不易设计太厚，根据设计及生产应用经验总结，S通常设计范围在1到2之间。

由公式(2)—公式(4)可得层状弹簧垂向刚度理论计算公式：

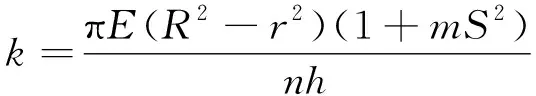
(6)

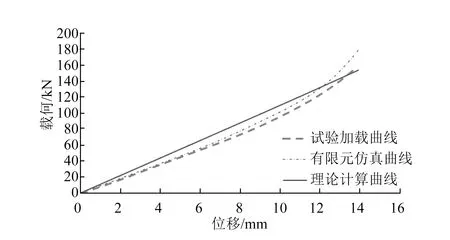
根据上述公式，对样品多种变形结构进行有限元仿真分析，得到多组样品结构参数与计算刚度的数据，对仿真数据取均方差值得到m的近似取值。当1.00

上述计算结果主要是针对某种普遍应用于轨道交通车辆层状弹簧的橡胶材料得出的结果，该类橡胶通常应用于轨道交通车辆用层状弹簧的橡胶硬度控制在50～70 Shore A之间。公式(6)为关键结构参数与层状弹簧垂向刚度的定量关系式，其为非线性定量关系。

3 验证分析

选取某轨道交通车辆用层状弹簧为研究对象，其技术要求AW0(空载)60 kN时垂向静态刚度为10 000 N/mm，AW2(满载)100 kN时垂向静态刚度为12 000 N/mm，公差均为±20%。基于层状弹簧空间尺寸要求，结合公式(6)设计了一种结构，计算刚度为12 643 N/mm。考虑同时符合空载和满载要求，可调整刚度到11 000 N/mm左右。调整过程中,避免增大层状弹簧的尺寸。结合R、r和h的变化对性能的定性影响规律，利用其规律进行结构参数调整，将R减小8.4%、r减小9.3%，同时将h减少5.9%，根据其结构计算单层橡胶的S值为1.73,所得层状弹簧结构计算刚度为11 230 N/mm。对改进后的结构进行有限元仿真计算。不同载荷下有限元仿真计算与公式计算的层状弹簧结构刚度对比如表2所示。

表2 不同载荷下有限元仿真计算与公式计算的层状弹簧结构刚度对比表

对该层状弹簧结构进行样品试制，并参考TB/T 2841-2010标准[12]中的试验方法进行常温下静态加载试验，得到垂向加载试验曲线。汇总3种不同方法得出的载荷位移曲线如图11所示。

由图11对比可以得出，有限元仿真分析结果曲线与试验加载曲线重合度较高，理论公式计算的曲线与试验加载曲线有较好的重合度。不同载荷下试验、有限元仿真计算、公式计算的层状弹簧结构刚度对比如表3所示。

图11 层状弹簧位移载荷曲线对比图

表3 不同载荷下试验、有限元仿真计算、公式计算的层状弹簧结构刚度对比表

由对比分析结果可以得出，在空载60 kN和满载100 kN时，采用理论公式计算的层状弹簧垂向刚度与试验验证结果偏差较小，在橡胶产品垂向刚度允许的偏差(±20%)范围内。基于理论公式计算和关键结构参数对性能定性影响规律，设计调整的层状弹簧结构可以满足技术要求。

综上所述，理论公式计算的垂向刚度值与试验结果较为接近，理论公式计算结合关键结构参数对层状弹簧垂向刚度性能的影响规律，可用于层状弹簧的设计开发指导以及既有层状弹簧结构垂向刚度的校核，有利于节省层状弹簧的设计开发进度及成本。

4 结论

1) 层状弹簧橡胶胶层外径R、橡胶胶层内径r、橡胶胶层厚度h以及橡胶层数n为影响层状弹簧垂向刚度性能的关键结构参数，这些参数对层状弹簧的垂向刚度有较直接的影响。其中，R对垂向刚度的影响规律为正向影响，其它参数均为负向影响，影响速率最大的是R。

2) 通过有限元仿真分析和试验数据总结出的垂向刚度理论公式的计算值与产品试验结果较为接近。理论公式计算结合关键结构参数对层状弹簧垂向刚度性能的影响规律，可用于层状弹簧的设计开发指导以及既有层状弹簧结构垂向刚度的校核。

3) 研究方法和结果有利于改善层状弹簧设计及优化过程进度和成本，有利于提高层状弹簧设计效率和优化改进效率。