基于Gamma过程的制动器磨损退化建模与>剩余寿命预测
梁庆海, 贾希胜, 白雲杰
(1.陆军工程大学 石家庄校区, 河北 石家庄 050003;2.中国人民解放军32153部队 教研部, 河北 宣化 075100)
制动器工作过程中,制动副之间的摩擦会使其摩擦表面材料不断脱落,这种现象即为制动器磨损。制动器磨损是其工作过程中摩擦现象导致的必然结果,但过度磨损会影响其制动性能,造成制动力矩下降,带来安全隐患。在缺乏精确预测的情况下,过早地对制动器进行维修或更换会造成资源浪费,也会降低设备的使用效率,而过晚实施维修或更换可能导致一些严重安全隐患。对制动器磨损性能退化进行建模研究,实现制动器磨损剩余寿命精确预测,能有效地进行预防性维修,降低维修成本,也可减少安全隐患。
常用性能退化建模方法有基于物理模型的方法、基于退化轨迹拟合的方法、基于随机过程和退化量分布拟合的方法等。制动器磨损是一种不可逆的累积过程,是摩擦副之间各种相互作用的综合结果。磨损本身是一个极其复杂的物理、化学过程,对其进行机理分析涉及材料、热力学、物理及化学等众多学科。不同材料摩擦副的磨损特性差异很大,即便是相同材料的摩擦副,不同工作环境下其磨损过程也呈现不同特点。因此,难以建立一个精确的物理模型对磨损过程进行退化建模以实现剩余寿命(RUL)预测。由于制动器的磨损受到制动材料、摩擦面外部杂质及环境温度、制动持续时间等工况的内外因素综合影响,其性能退化过程存在明显的随机性。最常用的描述产品性能退化的随机过程包括Wiener过程和Gamma过程等,Wiener过程模型能描述多种典型产品的性能退化过程,并且具有较好的计算分析特性。但Wiener过程是基于正态性假设的随机过程模型,对于一些严格单调的退化模型,通过Wiener过程并不能很精确地对其进行描述和分析。Gamma过程模型的增量具有独立、平稳、非负的特性,适用于描述具有非负增量、退化过程严格单调递增的产品性能退化过程,如机械部件磨损等。Abdel-Hameed M.的研究证明Gamma过程是一种适用于对设备进行磨损建模的模型。朱贝蓓等利用Gamma过程对碳化钨涂层的磨损进行建模研究,并实现了剩余寿命预测。考虑到制动器磨损深度呈单调递增趋势,其磨损性能退化是一个不可逆的累积过程,采用Gamma过程对制动器磨损进行性能退化建模,在此基础上进行制动器RUL预测。
1 基于Gamma过程的制动器磨损退化建模
1.1 模型描述
制动器磨损深度等于摩擦片原始厚度与当前厚度之差。在任意时刻t(t>0),制动器磨损深度为X(t),对应磨损增量为Y(t),假设过程{X(t),t≥0}和{Y(t),t≥0}为Gamma过程,则由Gamma过程的定义及性质可知制动器的磨损过程具有以下特性:1)Y(0)=0。2) 任意时刻t>0的磨损增量Y(t)=ΔX=X(t+Δt)-X(t),且不同时刻的Y(t)相互独立。3)Y(t)服从Gamma分布,其概率密度函数可表示为式(1)。
(1)

Gamma过程是一个增量非负且独立、服从Gamma分布的连续时间随机过程,当形状参数α为时间的线性函数α(t)时,该随机过程为平稳Gamma过程。此时,Y(t)的概率密度函数为:
fY(t)(y)=Ga(y|α(t),β)
(2)
其均值和方差分别为:
(3)
(4)
1.2 模型参数估计
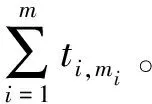
对于平稳Gamma过程,设ΔXi=Xi-Xi-1,Δti=ti-ti-1(i=1,2,…),用Ri=Δxi/Δti表示退化率,则通过退化率可计算样本均值和方差:
(5)
由式(3)~(5)可得:
(6)
进一步可求得:
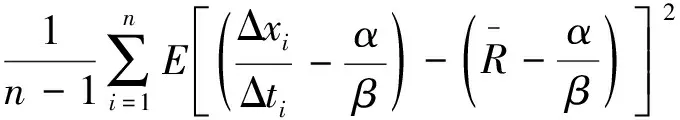
(7)
通过样本矩和期望值,可得:
(8)
(9)
求解式(8)和式(9),可得到参数估计值:
(10)
(11)
2 基于Gamma退化模型的制动器剩余寿命预测
2.1 寿命分布
对于累积退化过程,通常认为制动器的磨损退化过程X(t)一旦达到失效阈值Xceil(最大磨损深度)即发生失效。此时制动器因过度磨损已无法提供足够的制动力矩,导致制动距离过长,达不到安全性指标要求。据此,制动器失效时间可定义为X(t)的样本退化轨迹首次超过阈值Xceil的时刻,其寿命为从开始使用到首次达到失效阈值的时间段长度,表达式为:
T=inf{X(t)≥Xceil}={t|X(t)≥Xceil,
X(s)≤Xceil,0≤s≤t}
(12)
由Gamma退化过程样本轨迹的单调性,可进一步推导其寿命分布公式:
FT(t)=Pr{T≤t}=Pr{X(t)≥Xceil}=
(13)
式中:γ[α(t),Xceilβ]为上不完全Gamma函数,其定义见式(14)。

(14)
综上,进一步推导制动器磨损寿命的一阶矩及二阶矩分别为:

(15)

(16)
对式(13)、式(15)和式(16)进行求解,设qn=Pr{tn≤ΤXceil≤tn+1},并令tn=n/α,n=0,1,2,…,再对式(14)作离散时间近似,得:
(17)
式(17)表明,制动器在时间区间(n/α,(n+1)/α]内发生磨损超阈值而失效的概率是参数为Xceil/β的泊松分布,由泊松分布的性质可求出制动器磨损寿命的均值为Xceilβ/α,方差为Xceilβ/α2。
2.2 剩余寿命分布
制动器工作到时刻tc时,根据式(13),其剩余寿命分布为:
FT(t|tc)=Pr{T≤t|T>tc}=
(18)
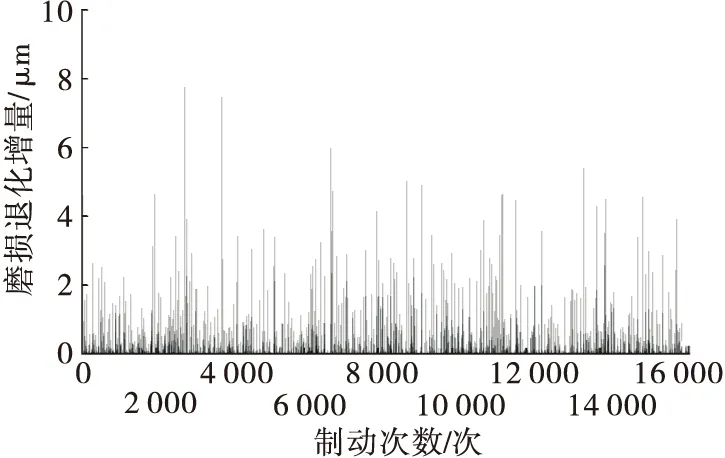
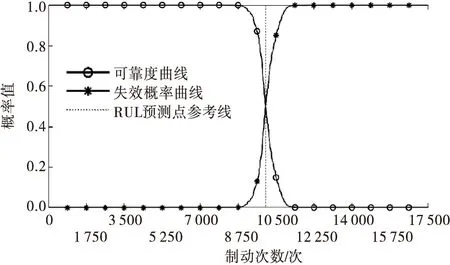
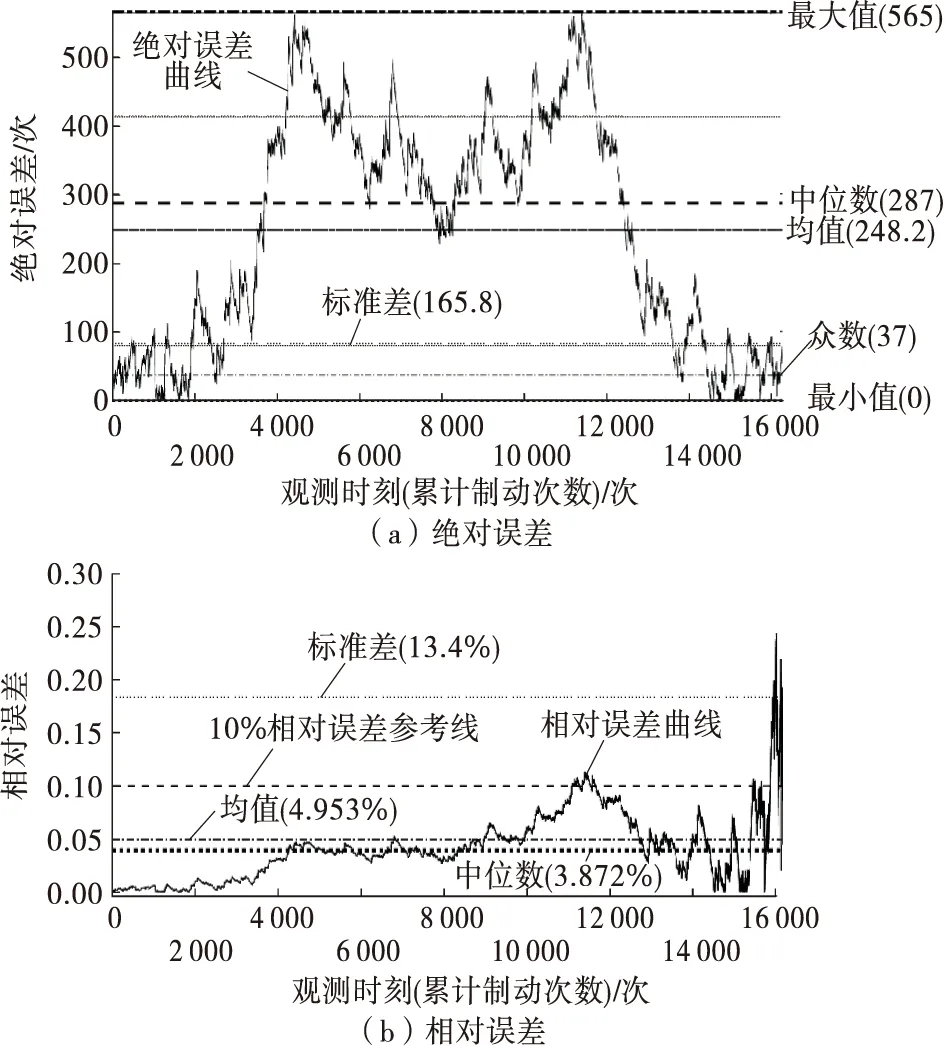
设制动器在时刻tc的磨损退化值Xc=X(tc) FT(t|tc)=Pr{T≤t|X(tc)=Xc}= Pr{X(t)-X(tc)≥Xceil-Xc}= (19) 假设制动器的寿命为T,由于制动器的磨损退化过程是一个单调递增过程,t时刻的可靠度函数为: R(t)=P(T>t)=P{X(t) (20) 为检验上述Gamma磨损退化模型的有效性,通过MATLAB进行仿真试验验证。生成一组制动器全寿命磨损退化数据,制动器摩擦片的累计磨损失效阈值为3 000 μm,制动操作造成的磨损量均值为0.178 6 μm/次、方差为0.294 9 μm2/次。每次制动所造成的磨损增量仿真数据见图1。 图1 制动器磨损增量仿真数据 累积磨损退化过程见图2,制动器在累计制动达16 398次时的累积磨损量为3 000.09 μm,此时制动器摩擦片的磨损寿命达到极限状态。 图2 制动器磨损退化过程仿真结果 图3 模型参数迭代更新过程 根据图2,在累计进行6 000次制动对应的观测时刻,累积磨损退化量为1 116.21 μm,下面预测从这一观测时刻到达磨损退化阈值Xceil=3 000 μm时的剩余寿命。根据Gamma过程的单调性和增量独立性,可由MATLAB的gampdf函数计算此后每次制动所对应时刻的概率密度函数值,并由此得到在这一观测时刻的RUL-pdf(概率密度函数)分布曲线(见图4)。 图4 累计制动次数为6 000次时的RUL-pdf曲线 根据仿真数据集,在累计进行6 000次制动时制动器的实际剩余寿命为16 398-6 000=10 398次。在图4的基础上,可根据剩余寿命的分布函数和可靠度函数进一步对制动器的工作可靠性进行分析,得到制动器的剩余寿命分布(见图5)。 图5 累计制动次数为6 000次时的寿命分布 用同样的方法和思路,在工作的全寿命区间的各观测时刻对制动器进行分析。在计算其累积磨损退化量的基础上,通过对历史磨损增量数据的统计分析,进行Gamma磨损退化模型参数估计,并进行制动器RUL预测,结果见图6。 由图3、图6可知:随着制动器工作时长的增加,累计制动次数不断增多,积累的可用历史监测数据不断增加,模型参数估计结果越来越稳定,RUL预测区间也不断收窄,说明根据模型对制动器进行磨损退化拟合基本符合仿真数据集的磨损特性。 图6 不同观测时刻的RUL分布 各观测时刻的RUL预测结果见图7。预测值与真实值十分接近,说明Gamma磨损退化模型能较好地对制动器磨损过程进行描述。 图7 不同观测时刻的RUL预测结果 RUL预测结果的绝对误差与相对误差见图8。 图8 不同观测时刻的RUL预测误差 由图8可知:虽然有少数预测值的相对误差超过10%,且在制动器工作寿命的末段RUL预测的相对误差增大,但由图7可知此时实际RUL已经较小,且在末段的RUL预测绝对误差基本在100次以下,此时用相对误差判断RUL预测精度已没有太大的实际意义。相对于所采用的制动器磨损仿真数据集,制动器全寿命总的制动次数为16 398次,RUL预测的绝对误差能控制在较小范围内。 对制动器磨损这一典型的性能退化过程建立基于Gamma过程的退化模型,在此基础上推导制动器剩余寿命分布函数和可靠度函数,通过制动器磨损的仿真数据集估计模型参数,根据新的磨损退化增量数据对模型参数进行更新,进而求解其寿命分布的概率密度函数值,并进行RUL预测。仿真试验结果验证了所建模型的可行性,且RUL预测精度较理想。在难以获取大量失效样本数据的情况下,文中研究可为工程实际应用中的制动器磨损退化建模与剩余寿命预测提供一种可行方法和思路,但仍需通过大量试验数据作进一步研究和验证。2.3 可靠度函数
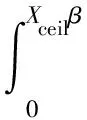
3 仿真试验
3.1 制动器磨损退化仿真数据

3.2 制动器磨损退化模型参数估计


3.3 制动器磨损退化的RUL预测



3.4 误差分析
4 结语

