基于线性自抗扰控制的自动驾驶车辆纵向加速度控制算法研究
陈国迎 赵选铭 文良浒 郑修磊
(1.吉林大学,汽车仿真与控制国家重点实验室,长春 130025;2.吉林大学,汽车工程学院,长春 130025;3.中国人民解放军63612部队,敦煌 736200)
主题词:自动驾驶车辆 纵向加速度 线性自抗扰控制 递归最小二乘法 卡尔曼滤波
1 前言
纵向加速度跟踪是实现自动驾驶运动控制的关键环节,是开发自适应巡航控制(Adaptive Cruise Control,ACC)系统和协同自适应巡航控制(Cooperative Adaptive Cruise Control,CACC)系 统等的基础[1-3],因此,实现高性能的纵向加速度控制具有重要意义。
国内外研究机构针对纵向加速度跟踪已展开了深入研究。宾洋等设计了基于滑模变结构控制(Sliding Mode Control,SMC)的模型匹配控制器,主要针对车辆在低速起停工况下的加速度控制[4]。高锋等提出了基于不确定性估计的切换指标函数,实现了汽车纵向加速度多模型分层切换控制[5]。陈书锦等结合永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)的特点,建立了驱动系统受控自回归滑动平均(Controled Auto Regression and Moving Average,CARMA)模型,采用递推最小二乘法辨识模型参数,实现了广义预测PI 控制方法对加速度的控制[6]。李贻斌等使用自抗扰控制方法设计了车辆纵向加速度控制器[7]。阮久宏等利用二阶线性自抗扰控制方法分别设计了发动机和制动器与车辆加速度系统之间的控制器,从而实现了对车辆加速度的控制[8]。朱增辉等采用模糊控制方法,分别设计了油门执行机构模糊控制器和制动系统模糊控制器,从而实现了对不同期望加速度的快速跟踪[9]。Kim等通过改进的线性化车辆模型设计自适应控制律,提出了基于时变参数的自适应加速度控制器[10]。熊璐等利用自适应遗忘因子递归最小二乘法对道路阻力进行估计,在此基础上设计耦合的车速和加速度控制律,实现了对期望速度和期望加速度的同时跟踪[11]。
由于车辆纵向动力学系统的高度非线性,上述成果对纵向加速度控制算法的研究主要集中在抑制外部干扰和减少模型不确定性的影响上,本文在此基础上提出基于线性自抗扰控制(Linear Active Disturbance Rejection Control,LADRC)且具有双观测器结构的电动汽车加速度控制算法,并利用带有遗忘因子的递归最小二乘(Recursive Least Squares,RLS)法设计电机与制动器的切换策略,通过硬件在环测试验证控制算法对加速度控制的鲁棒性和跟踪性能。
2 车辆纵向加速度系统模型
2.1 车辆纵向运动模型
根据车辆纵向运动过程中的受力状态,在不考虑纵向和侧向耦合的情况下,车辆纵向受力可以简化为如图1所示的模型。

图1 车辆纵向受力模型
车辆整体纵向运动方程为:

式中,Ft为驱动力;Fw0为空气阻力;Ff0为滚动阻力;Fi0为坡道阻力;Fj0为加速阻力。
将车辆纵向受力带入式(1)可得:
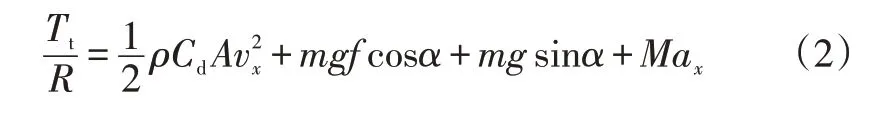
式中,Tt为驱动力矩;ρ为空气密度;Cd为空气阻力系数;A为迎风面积;g为重力加速度;f为滚动阻力系数;m为车辆质量;vx为纵向车速;R为车轮半径;ax为纵向加速度;M为包含旋转质量的车辆等效质量;α为坡角。
2.2 PMSM模型
PMSM的运动方程[12]可以描述为:
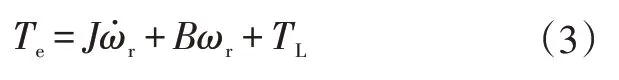
式中,Te为电机转矩;ωr为电机角速度;B为阻尼系数;J为转动惯量;TL为负载转矩。
将式(3)两侧对时间求导,得到PMSM-加速度系统的二阶仿射模型:

式中,Fψ0=Ff0+Fi0为道路阻力;Fψ为道路阻力扰动;Fw为空气阻力扰动;i为传动比。
2.3 制动器模型
制动器建模主要考虑制动压力到制动力转换环节中的液压系统建压滞后过程,因此制动器模型可以简化为一个带迟滞的一阶惯性环节[13],所以制动器模型为:

式中,Fb为制动力;Kb为制动器增益;u为制动压力;t0为时间常数。
将式(5)两侧对时间求导,可以得到制动器-加速度系统的二阶仿射模型:

式中,Tb为制动力矩。
3 线性自抗扰加速度跟踪控制器设计
3.1 加速度线性自抗扰控制算法
自抗扰控制(Active Disturbance Rejection Control,ADRC)的思想是把系统的未建模动态和未知外扰作用都归结为对系统的总扰动而进行估计并给予补偿[14],但ADRC 的参数多且整定困难,不便于实际工程应用,为此,本文采用LADRC,其不仅继承了ADRC 的抗扰特性,而且使参数得以简化。LADRC 主要由线性扩张观测器(Linear Extended State Observer,LESO)和PD 控制律组成,通过LESO 对系统扰动的估计和反馈以及PD控制的共同作用来实现对系统的控制[15],如图2 所示。其中:r0为参考输入;u0为PD控制律的输出;y、uc分别为控制对象的输出和输入;Z1、Z2分别为y及其一阶微分的估计值;Z3为总扰动的估计值;b为系统控制输入的增益。

图2 LADRC结构
一个简单二阶系统可以描述为:
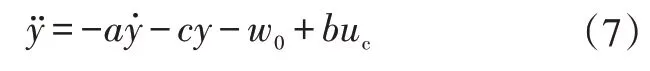
式中,a、c为参数;wo为外部扰动。
当a、c未知时,可以将模型简化为:

式中,f0为总扰动。
若以驱动力矩和制动力矩作为输入,加速度作为输出,将式(4)和式(6)与式(8)进行类比可得PMSM∕制动器-加速度系统的扰动f1、f2和输入增益b1、b2分别为:

当对车辆加速度系统进行线性自抗扰控制时,可以通过LESO 对扰动f1、f2进行估计并反馈,同时将输入增益b1、b2作为可调参数,因此不需要准确的车辆纵向动力学模型,从而可以很好地解决加速度控制中系统的非线性和不确定性带来的问题。从工程应用角度出发,采用离散形式的LADRC 算法,其LESO 和PD 算法公式分别为:

本文的LADRC算法需要车辆反馈的纵向加速度信息,采用2 种方式获取:通过传感器直接测量和利用传感器测量的纵向速度信息对加速度进行估计。由于传感器测量信号带有噪声,本文采用卡尔曼滤波对测量信号进行滤波处理,同时利用卡尔曼滤波通过纵向速度实时估计车辆的加速度。卡尔曼滤波算法的公式为:
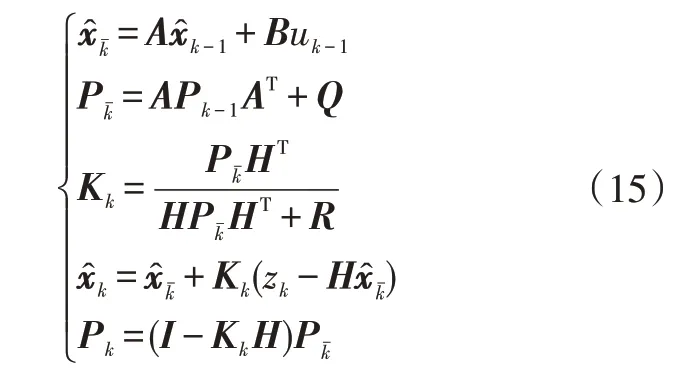
2 种方式获得的加速度信息在不同的车辆状态下存在差异,对车辆进行侧倾和俯仰测试,车速从0 开始逐渐增加,测试结果如图3所示,可以看出,通过传感器直接获得的加速度受车辆侧倾和俯仰的影响较大,其更能反映车辆所受的扰动,利用速度估计得到的加速度虽然较测量值存在一定的延时,但其受车辆侧倾和俯仰的影响较小,更接近真实值。

图3 2种方式获取的加速度对比
本文在LADRC结构的基础上采用双LESO的设计,如图4 所示。PD 控制属于动态跟踪控制,与其对应的LESO 的输入在不同车辆状态下应更加接近真实值,所以选择加速度估计值作为输入;但对于扰动补偿环节,LESO所估计的扰动量应更好地反映车辆所受到的真实干扰,其对应的输入到LESO的加速度信号也要准确地包含车辆所受到的扰动信息,因此选择加速度测量值作为输入。这样的双LESO 设计可以充分利用加速度测量值和估计值各自的优势,提高LADRC 算法的抗扰能力和控制效果。
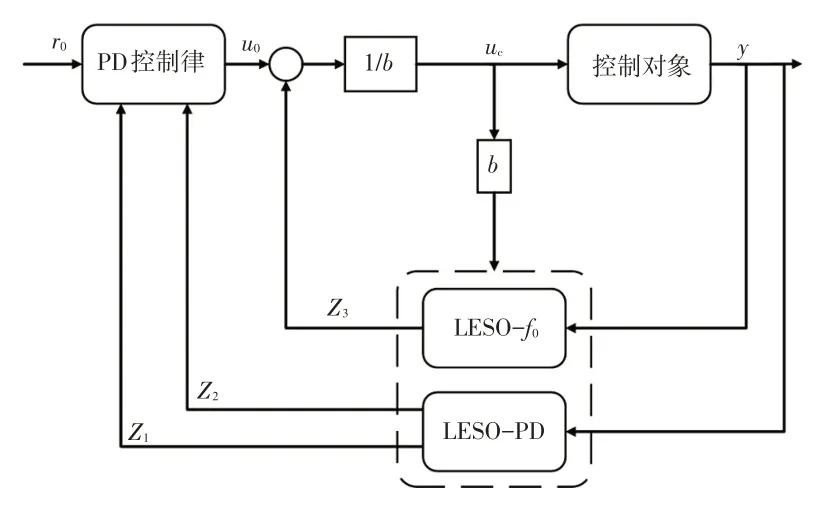
图4 双LESO结构的LADRC
3.2 电机-制动器切换逻辑
本文利用期望加速度ad与外部阻力(道路阻力与空气阻力之和)所产生的加速度ae之间的关系来决定驱动或制动,同时为了避免信号波动引起电机与制动器之间的频繁切换,在ae附近设置切换裕度as。如图5所示:当ad>ae+as时,电机工作;当ad<ae-as时,制动器工作;当ae-as≤ad≤ae+as时,车辆处于滑行状态,电机和制动器均不工作。
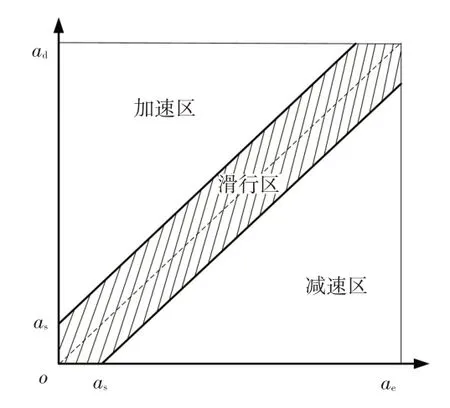
图5 切换策略示意
对于ae的确定,由于LESO 观测的扰动包含内扰和外扰且不易分离,因此无法用其估计外部阻力。本文通过带有遗忘因子的RLS法识别外部阻力,其很好地保留了最小二乘法程序简单、易于实现等优点,同时又很好地解决了最小二乘法在进行系统参数实时辨识方面占用大量内存和运算能力的问题,因而具有遗忘因子的RLS算法已广泛应用于时变系统识别中[16]。RLS法的核心思想可以表述为:使用当前时刻的观测数据对上一时刻的辨识结果进行修正,从而得到新的辨识结果。
令Y=Ft-Fj0、w=Fψ0+Fw0,将式(1)整理成最小二乘格式Y=w+we,其中we为过程白噪声,最后通过具有遗忘因子的RLS算法得到:
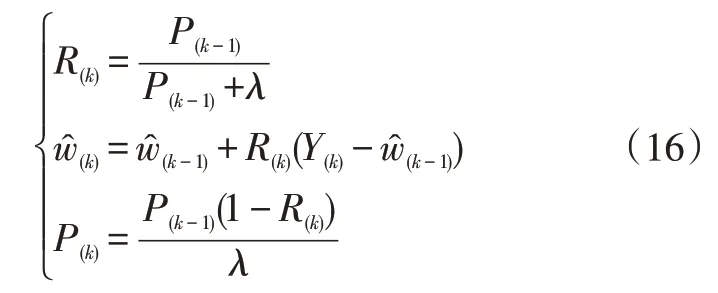
式中,R(k)为递推增益;P(k)为协方差;λ为遗忘因子,取值区间为(0,1],并按一定的规律变化;w^(k)为外部阻力估计值。
当期望加速度变化时,车辆的纵向加速度系统会进行动态响应,此时通过RLS算法得到的道路阻力估计值与真实值偏差较大,为此,需要设定一个较大的信任度衰减,即此时选取的遗忘因子数值较小,随着辨识的不断进行,系统达到稳态,辨识结果会收敛到实际值附近,则此时需要较大的遗忘因子,以获取较小的信任度衰减。
加速度线性自抗扰控制整体结构如图6 所示。其中,ax1和ax2为卡尔曼滤波器输出的加速度,力矩T经切换策略转换成驱动力矩Tt和制动力矩Tb。

图6 加速度线性自抗扰控制器结构
4 HIL测试分析
为了验证本文控制算法的有效性,搭建了HIL测试平台,如图7所示,其由上位机、dSPACE 1103实时仿真系统、MicroAutoBox II 1401∕1507原型控制器、Sensodrive力矩转向盘模拟器组成。

图7 HIL实时测试平台
Sensodrive力矩转向盘模拟转向路感并采集驾驶员的转向盘操纵信息;dSPACE 1103实时仿真系统作为模拟器核心运算单元运行CarSim RT;上位机通过TCP∕IP与dSPACE 1103 连接,主要完成模型的编译和下载,主显示器提供驾驶场景显示以及显示利用ControlDesk 搭建的车辆状态数据监测界面;MicroAutoBox II 1401∕1507 作为线性抗扰加速度算法的原型控制器硬件平台,通过500 kbit∕s CAN 总线与dSPACE 1103 实时仿真系统进行信息交互。
本文设计了3 种典型工况对提出的加速度控制算法的跟踪能力以及车辆侧倾和俯仰扰动的抑制能力进行验证。
4.1 工况1 加速度跟踪能力验证
在附着系数为0.85的水平路面上,设车辆初速度为10 km∕h,沿直线行驶,验证结果如图8所示。
由图8 可知,本文提出的控制算法能够对期望加速度信号实现快速、稳定的动态跟踪,超调量小于0.25 m∕s2,稳态误差在±0.03 m∕s2以内,这表明该算法对于车辆纵向动力学系统的非线性和模型的不确定性具有良好的适应能力。
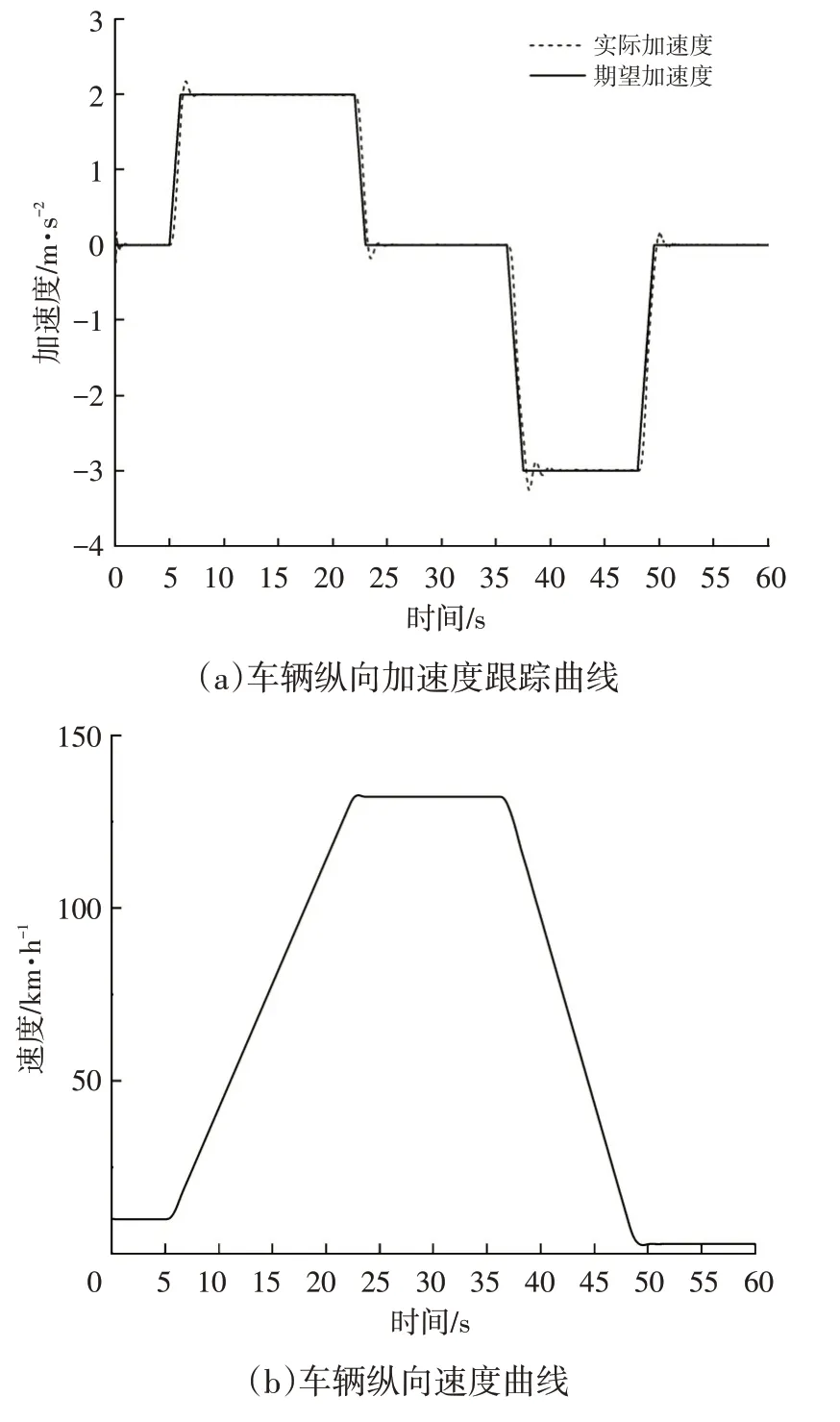
图8 工况1验证结果
4.2 工况2 侧倾扰动抑制能力验证
在附着系数为0.85的水平路面上,设车辆初速度为5 km∕h,对车辆前轮施加10°的恒定转角进行转弯行驶,验证结果如图9所示。
由图9可知,车辆纵向加速度的超调和稳态误差较小,因此在车辆转弯产生侧倾影响的情况下,控制器能够抑制侧倾扰动,从而对车辆加速度进行稳定的跟踪控制。

图9 工况2验证结果
4.3 工况3 俯仰扰动抑制能力验证
测试道路如图10 所示,由水平路面和坡度角为6°的路面组成,附着系数为0.85,设车辆以30 km∕h的初速度在道路上沿直线行驶,期望加速度设置为0,验证结果如图11所示。
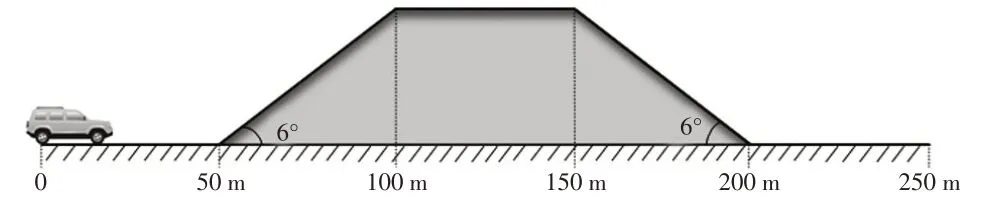
图10 工况3道路模型
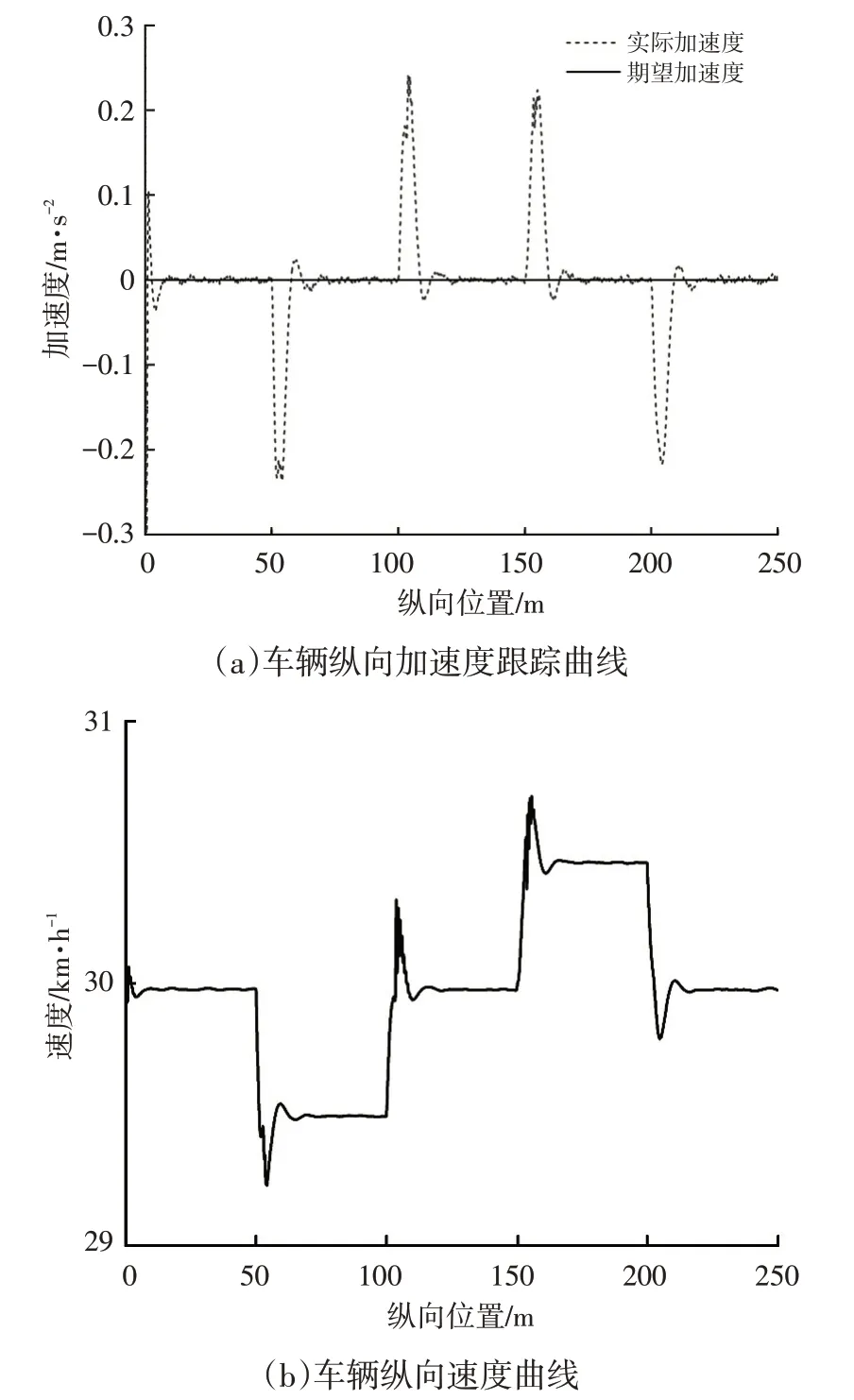
图11 工况3验证结果
从图11 中可以看出,当车辆在不平路面上行驶受到俯仰运动的干扰时,本文设计的控制算法能够对俯仰扰动进行快速响应,控制车辆对期望加速度进行稳定跟踪,车速误差保持在±1 km∕h以内,这说明本文的控制算法能够抑制车辆俯仰对纵向加速度控制所带来的影响。
5 结束语
本文提出了基于LADRC 的纵向加速度控制算法,在LADRC结构的基础上设计了双LESO结构,并基于带有遗忘因子的递归最小二乘法设计了驱动电机与制动系统之间的切换逻辑。通过硬件在环验证可以得到以下结论:
a.本文的控制算法对于电动汽车加速度系统的非线性与不确定性产生的内扰以及外部环境变化、车辆侧倾和俯仰产生的外扰具有良好的适应能力,从而实现对加速度信号快速、稳定地跟踪。
b.在车辆纵向动力学模型未准确建模状态下,本文的算法可以对纵向加速度进行有效控制,且具有很强的鲁棒性,可以用于车辆队列控制、自适应巡航控制等。

