基于连续时间的二阶多智能体分布式资源分配算法

时侠圣 杨 涛 林志赟 王雪松

随着控制技术的发展,将控制技术与优化算法相结合,以分布式方式求解网络优化问题成为近年来的研究热点[1-7].作为网络优化领域里一个重要分支,资源分配在网络系统中有很广泛的应用,例如能源系统中的经济调度和通讯网络中的网络利用率最优化等问题.

近些年来,基于离散时间算法的分布式优化问题已经得到了一些很好的结果.例如,文献[8-10]等针对有约束或无约束最优协调问题设计了一种基于梯度的算法.而对于强连通有向网络下的资源分配问题,文献[11-13]等基于多智能体一致性理论,分别设计一种基于余量和基于Push-sum (推和)的分布式优化算法.更多离散时间算法可参考文献[14-19]及它们的引用文献,其中收敛速度最快的为文献[17]的线性收敛,但是依然无法预知其收敛时间.另一方面,随着信息物理系统和连续时间控制技术的发展[20-25],利用基于连续时间的分布式控制策略也已被广泛应用于解决资源分配问题,特别是其中的有限/固定/预定时间收敛理论,更符合实际系统需求.为了解决无向网络下的无约束资源分配问题,基于多智能体一致性理论,文献[26]设计了一种指数收敛速度二阶连续时间算法.不同于文献[26]的渐近式收敛,文献[27-30]分别设计一种基于固定时间和预定时间收敛的连续时间算法.在此基础上,文献[31-35]提出了一种考虑不等式约束的分布式算法,该算法利用映射算子将节点状态限制在不等式约束集合内,从而得到了一种无初值约束分布式算法,并在文献[35]中实现了固定时间收敛.与映射法不同,文献[36-38]和文献[39]利用精确罚函数法将局部等式约束转移到目标函数中,分别设计了一阶和二阶连续时间算法.而对于有向网络下的资源分配问题,也有很多学者提出了解决方法,例如奇异摄动算法[40]、原始对偶算法[41]、映射法[42]、二阶连续时间算法[43]以及微分映射法[44].

从前面的讨论可以看出,目前只有一阶分布式优化算法在连续时间和离散时间情况下都取得了显著的效果.而有关二阶多智能体分布式优化算法的文献不是很多.其中文献[26,45-46]研究了无约束资源分配问题,并没有将节点局部不等式约束考虑进来.但在许多工程应用中,节点的决策会受到局部约束,这些约束可能来自安全考虑、生产能力、执行能力等,如电力系统中发电机的输出功率的边界限制[1].文献[39]和文献[43]分别利用精确罚函数法和微分映射法解决了资源分配问题中的局部不等式约束.但是上述两篇文献所提出的算法都对初始状态进行限定.而这种初始化协调过程可能只适应于静态网络.然而对于一个动态网络来说,一旦网络发生变化或者节点生产约束发生突变时,就必须重新分配资源配置更改.因此这些优化算法重新启动时,必须重新进行初始化协调,这大大降低了它们的适用性.此外,文献[26,39,45-46]中考虑的都是无向网络.

然而,由于通信延迟等造成的通信中断会使得无向网络变成有向网络,进而可能会使得一些基于无向网络的分布式算法失效.另外,无向网络是有向平衡网络的一个特例,在工程应用中,有向平衡网络比无向网络也更易于实现,因此研究有向平衡网络上的资源分配问题是有意义的.由于二阶多智能体系统的广泛存在,如:移动机器人、发电机等,本文考虑二阶多智能体的分布式资源分配问题.针对有向平衡网络下的资源分配问题,本文首先利用局部不等式及其梯度设计第一种算法,其次利用固定时间理论和映射算子设计第二种算法,其中映射算子用于处理不等式约束,且确保此不等式在固定时间内即可满足,此方法可推广到同类型带局部不等式约束的分布式优化问题中.

本文所提算法创新点如下:

1) 相比于文献[26,45-46],本文将二阶多智能体节点的局部不等式约束考虑进来;

2) 与文献[39]的无向网络相比,我们研究有向平衡网络下的资源分配问题;

3) 相比于文献[43],本文所提两种算法均对初始值无要求,且分别实现渐近和指数收敛;

4) 针对节点局部不等式约束,本文结合了固定时间收敛理论和映射算子,使得收敛速度上会比单纯使用映射算子方法的算法要快,并通过案例仿真可以验证此性质.

本文后续内容结构如下:在第1 节中,将完成问题描述以及预备知识,其中预备知识包括代数图论、固定时间收敛理论等;在第2 节中,首先进行算法设计,分别是渐近收敛算法和指数收敛算法,其次给出相应的最优性引理以及各自算法的收敛性分析;在第3 节中,给出3 个仿真案例;本文的总结与展望放在第4 节中.

1 问题描述及预备知识

1.1 问题描述

本文所研究的二阶多智能体系统包含n个智能体节点,每个智能体i都采用如下动力学模型:

1.2 代数图论

针对式 (1)所示的多智能体系统,智能体节点间的通信链路可以用图G=(V,E,A) 表示,其中V={1,2,···,n} 表示节点集合,E表示节点间的通信链路集合,A表示各节点间的通信权重.若存在有向对 (i,j)∈E,则表示节点i能够接收到来自节点j的信息,此时就有aij＞0.此外,本文中不考虑节点存在自环,即aii=0.若网络G中存在一组有向对 (i,i1),(i1,i2),···,(ik,j),则称节点j到节点i是可达的.若网络G任意一点到其他节点都是可达的,则称网络G是强连通的.定义网络G的拉普拉斯矩

2 分布式连续时间控制算法

针对问题 (2),基于多智能体固定时间理论,本节将设计两种基于映射的分布式优化算法,首先设计一类渐近收敛算法,其次设计一类指数收敛算法,并给出算法的收敛性分析.

2.1 算法设计

由引理1 可知,解决问题 (2)的关键是找到最优拉格朗日乘子.为实现算法分布式演化,本文为每个智能体都分配一个本地拉格朗日乘子λi∈Rm,基于状态反馈和梯度下降法,利用局部不等式约束的梯度信息,每个节点将通过以下算法自主收敛到问题 (2)的最优分配方案:

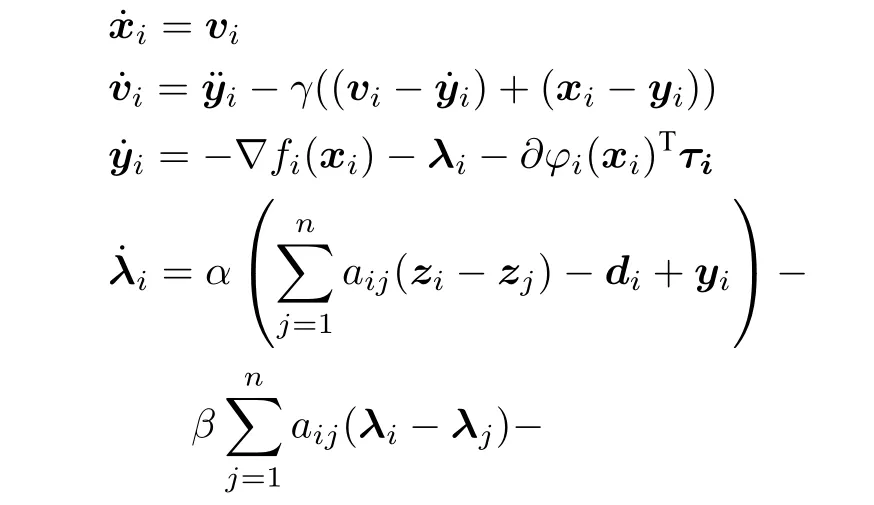
2.2 算法收敛性分析

3 案例仿真

现在我们提供仿真案例来验证之前所提算法的有效性.第一个案例数据来自文献[43],第二个仿真案例数据来自文献[44].

案例 1.针对6 发电机系统,每个发动机的代价函数采用如下二次函数形式:各发电机代价函数系数、初始值xi(0)、期望功率di和输出功率约束总结在表1 中.令算法(8)和算法(9)中控制参数为α=2.75,β=380,γ=30,μ=0.5,ν=2.从任意初始状态出发,详细的仿真轨迹分别如如图1和图2所示,从图中可知问题的最优值为x*=[23.01;35;50;31.01;45.78;30.19]T,此结果与文献[43]一致.相比于算法(8)中的梯度法,由于算法(9)采用映射算子和固定时间收敛理论处理问题(2)中的局部不等式约束,所以算法(9)可以很快地将超出约束范围的节点快速拉回到约束范围内.所以图1 相比图2,在算法到达约束边界时,有更大的波动性.基于案例1 中的数据,接下来从同一初始状态出发,将本文所设计算法与文献[43]和文献[39]进行收敛速度对比,结果如图3 所示(文献[43]中控制参数设置与本文相同).其中算法误差定义为,其中最优值由集中式拉格朗日乘子法求得.则e表示算法运行解与理论最优解的差值.从图3 可以看出,本文所设计算法下误差下降较快,即拥有更快的收敛速度,且算法在稳定点时有更好的稳定性.而文献[39]由于在端点处梯度不唯一,会导致算法在稳定点时有轻微波动.此外,算法 (9)和文献[39]在边界点的波动性导致其误差e要比算法 (8)和文献[43]中的误差稍大.

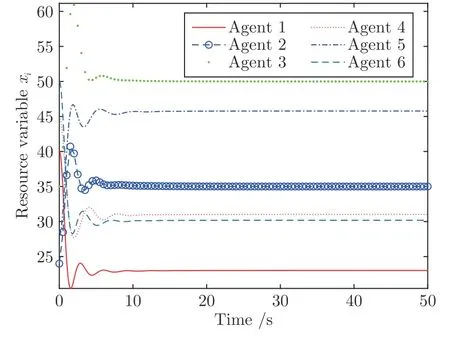
图1 案例1 中算法(8)的各发电机曲线图Fig.1 The trajectories of each generator by algorithm (8) in case 1

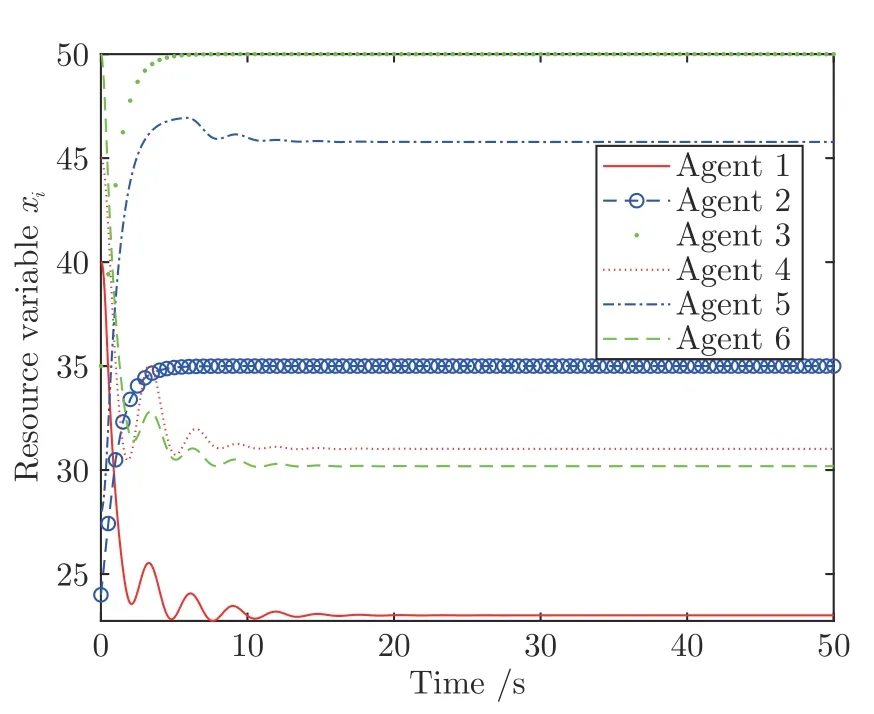
图2 案例1 中算法(9)的各发电机曲线图Fig.2 The trajectories of each generator by algorithm (9) in case 1

图3 基于案例1 数据的算法性能对比Fig.3 The comparison between the existence algorithms and ours based on case 1

表1 案例1 各节点参数Table 1 System parameters in case 1

案例2.针对4 节点环形网络,其中资源决策变量xi∈R2,且节点目标函数分别为

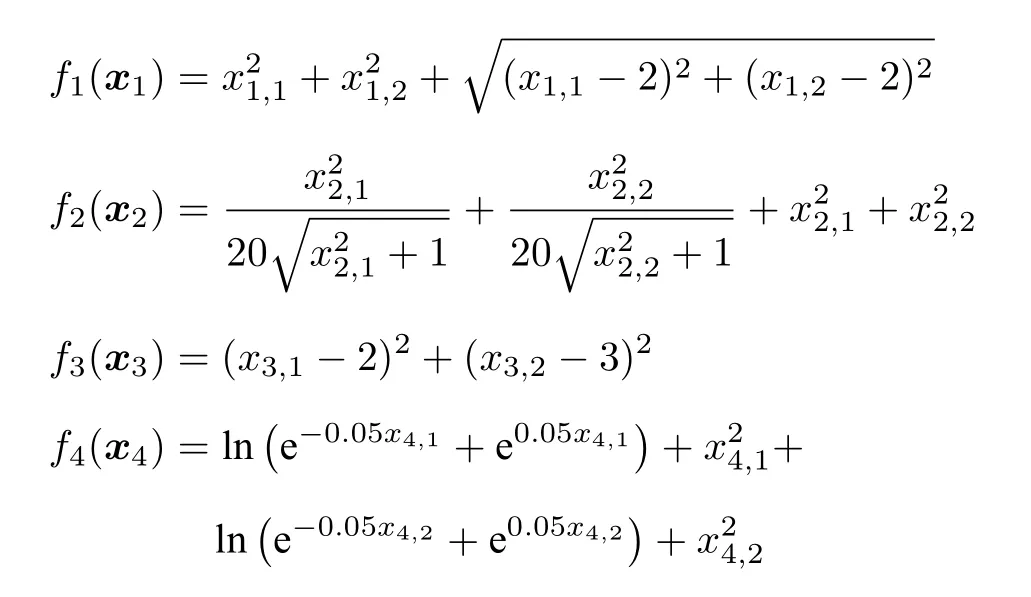
其中

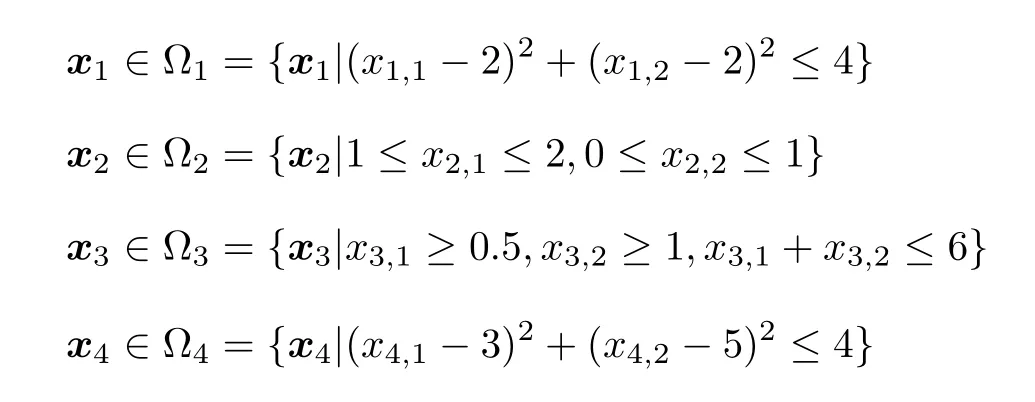
虚拟资源量d设定为d1=[2,1]T,d2=[2,3]T,d3=[2,4]T,d4=[1,5]T.算法初始值设定为x1(0)=[2,0]T,x2(0)=[1.5,0.5]T,x3(0)=[1,1]T,x4=[4,6]T,算法控制参数设定为α=2,β=75,γ=30,μ= 0.2,ν=2.其仿真曲线分别如图4 和图5 所示,星点表示各节点的最优解位置.通过仿真案例2 可以发现,本文所设计算法对高维资源分配问题亦是有效的.为了展示各算法在二维资源分配问题上的收敛速度,现将本文所设计算法与文献[43]进行对比,收敛速度图展示在图6,从图中可以看出,指数收敛算法 (9)比渐近收敛算法 (8)收敛稍快,该结果与一维资源问题图3 所得结论一致.

图4 案例2 中算法 (8)的各节点仿真结果轨迹Fig.4 The trajectories of each agent by algorithm (8) in case 2

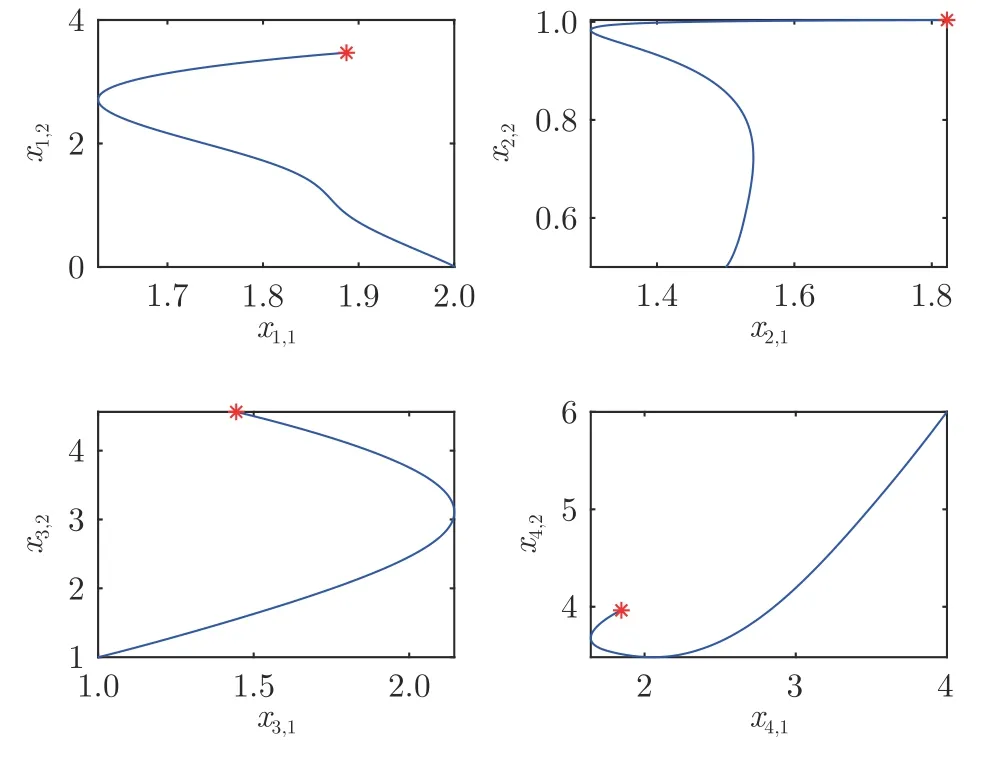
图5 案例2 中算法 (9)各节点仿真结果轨迹Fig.5 The trajectories of each agent by algorithm (9) in case 2

图6 基于案例2 数据的算法性能对比Fig.6 The comparison between the existence algorithms and ours based on case 2

案例3.针对IEEE-39 总线系统,包含10 个发电单元,各发电单元的通信链路及其权重如下图7 所示.各发电单元的发电成本为且有a1=[0.096 0.082]T∈R10和a2=[1.22,3.41,2.53,4.02,2.90,0.072,0.105,0.082,0.078,0.90,0.085,0.092,0.155,2.72,1.22,4.20,3.53,3.02]T∈R10,其中a1=[a1,1,···,an,1],a2=[a1,1,···,an,1]∈R10.各节点的局部不等式约束和虚拟分配量分别为xi∈[0,300] 和di=250.以零初始状态出发,在控制参数α=2.75,β=380,γ=30作用下,算法 (8)和 (9)各自对应的状态轨迹如图8 和图9 所示.此外两种算法的误差e轨迹如图10所示,其中误差e定义同案例1.从图10可知,上述系统最终收敛到最优分配方案x*=[243.6524,300,216.5298,268.1785,289.1107,251.5626,275.1839,238.0504,143.4557,274.2760].

图7 案例3 中各发电单元的通信链路Fig.7 The communication links of each generator in case 3

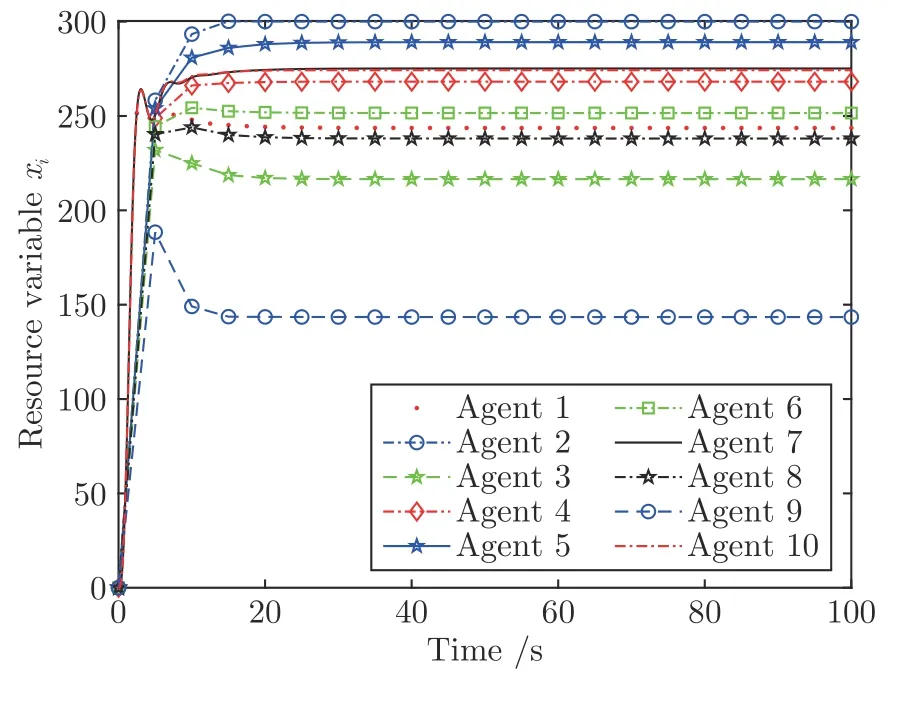
图8 案例3 中算法 (8)的各节点仿真结果轨迹Fig.8 The trajectories of each agent by algorithm (8) in case 3

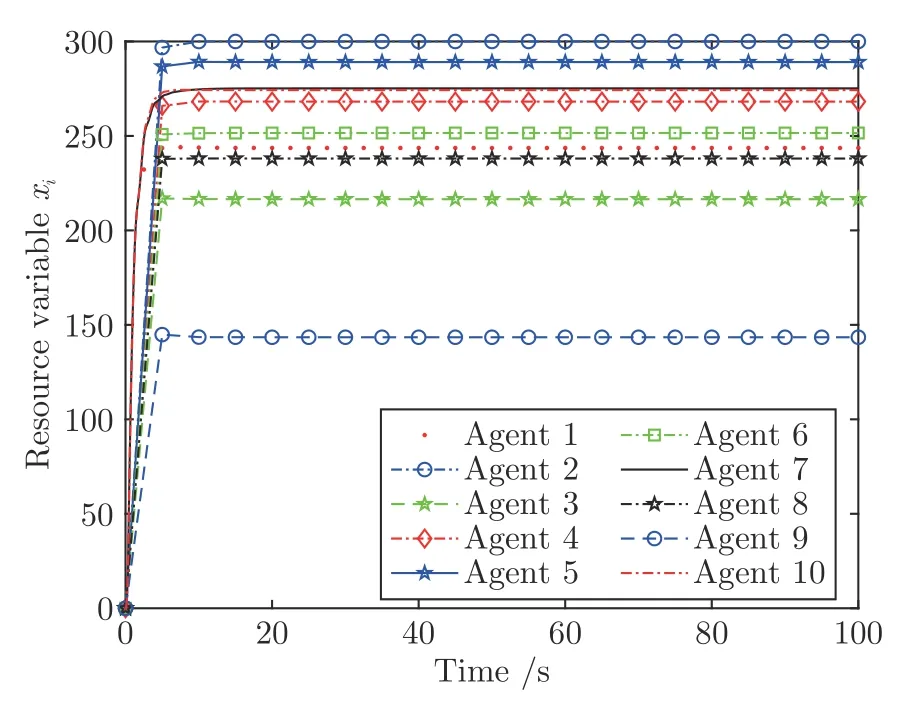
图9 案例3 中算法 (9)各节点仿真结果轨迹Fig.9 The trajectories of each agent by algorithm (9) in case 3

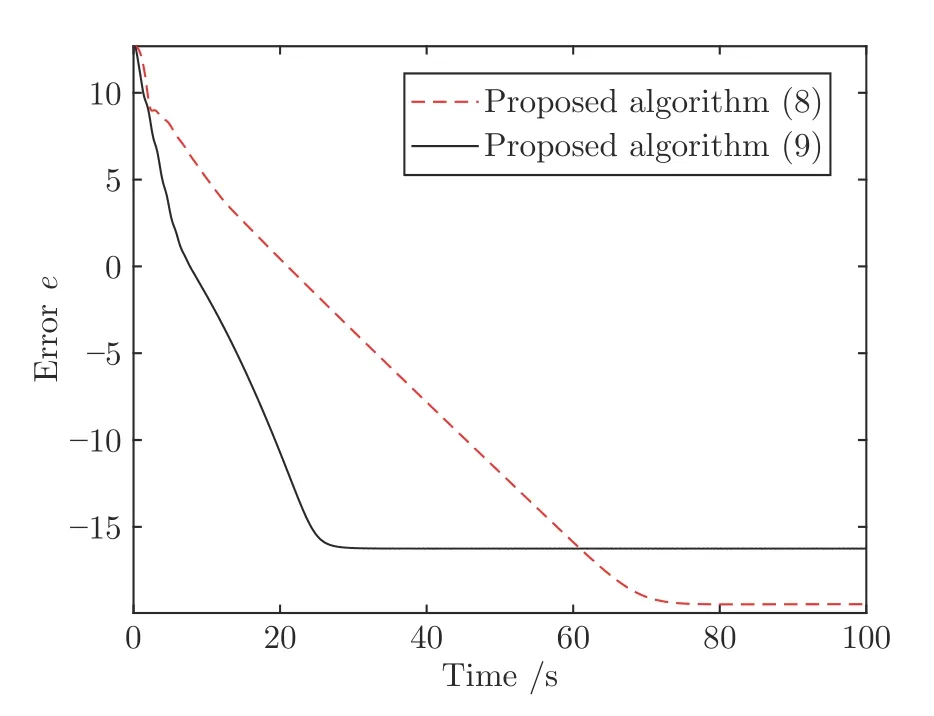
图10 案例3 中算法 (8)和 (9)的收敛速度比较Fig.10 The convergence rate comparison between algorithms (8) and (9) in case 3

4 总结

本文针对有向平衡网络下的带约束分布式资源分配问题,基于固定时间映射算子和基于多智能体一致性的梯度下降法,设计了两种基于二阶多智能体系统的连续时间算法.所设计算法对节点初始状态无约束,并且控制参数全为常数.通过对一维和二维资源分配问题数值仿真,本文所提算法的有效性也得以保证.然而在实际系统中,通信网络通常会存在信息交互延迟,而信息延迟给算法分析带来了很大的困难.此外,非平衡有向网络在实际系统中也是存在的,所以在后续研究中,我们将考虑由通信延迟等造成的有向非平衡网络下二阶多智能体资源分配问题.