基于随机配置网络的井下供给风量建模

王前进 杨春雨 马小平 张春富 彭思敏

主通风机切换过程(Main fan switchover process,MFSP)被广泛用来保证矿井的持续安全生产[1].矿井必须配有成对的主通风机,采用轮流运行的工作模式.其中,运行的一台叫工作主通风机,另一台叫备用主通风机.井下供给风量作为主通风机切换过程的关键运行指标,对井下作业影响很大,因此有必要对其进行实时监测,保证主通风机切换过程的平稳运行以提供充足的井下供给风量.然而,由于恶劣的井下工作环境,取压孔容易出现堵塞现象,导致无法实时准确地监测井下供给风量状态.另外,堵塞的取压孔必须等到大周期(一般半年或一年一次) 的主通风机检修才能进行取压孔的清理.因此有必要建立井下供给风量的准确可靠性模型,为矿井值守人员提供井下工作状况和供给风量信息.

目前井下供给风量模型主要分为两大类:机理模型和数据驱动模型.主通风机切换过程涉及到两大动力源的过渡,涉及到 4 个风门的切换,涉及到井下供给风流的控制等.因此,井下供给风量机理模型包括:主通风机模型可用其特性曲线来表示[2];对于风门支路,首先通过数据拟合方法建立风门风阻与风门开度之间的非线性关系,再采用定常[3-4]或非定常[5-6]不可压缩Navier-Stokes 方程来建模;对于地下矿井,由于复杂多变的井下工作环境和错综复杂的网络布局以及频繁变化的设备状态,难以建立模型.通常首先将其近似为一个长度确定的风流支路,再采用类似于风门支路的建模方法来建模.井下供给风量模型是由上述主要结构的子模型组成,通过基尔霍夫风压和风流定律来建立.然而,由于机理模型一般是基于一定的理论假设而建立的,如地下矿井的近似化处理,实际主通风机切换过程要远远复杂于机理模型,因此机理模型在实际主通风机切换过程中往往难以应用.数据驱动的井下供给风量建模方法,不需要掌握切换过程的复杂变化,仅利用数据就可以建立井下供给风量的估计模型,因此数据驱动井下供给风量建模是目前主通风机切换过程建模研究的热点.如,文献[7]利用静态工况下的井下供给风量和风门分支风门风阻的数据,建立了基于RBF 神经网络的井下供给风量模型.

近年,由于具有极快的学习速度,且能有效地解决传统神经网络收敛速度慢、易陷入局部极小的问题,增量式随机权网络(Incremental random weight network,IRWN)已被广泛用于复杂工业过程的建模[8-10].IRWN 本质上是一种采用构造算法得到的单隐层前馈神经网络(Single layer feedforward neural network,SLFNN),比传统神经网络具有更简单的结构和更高的计算效率[11].针对IRWN 收敛性问题,文献[12]通过对一类IRWN 进行理论分析和仿真研究,得出一个结论:IRWN 的万能逼近能力只有在一定的约束条件下才能得到保证.因此,寻找保证IRWN 收敛性的约束条件是建立IRWN 的关键.如,文献[13]提出了一种基于不等式约束条件的随机配置网络(Stochastic configuration network,SCN),其不仅具有万能逼近能力,而且具有较快的学习速度.与标准IRWN 相比,SCN 算法具有较快的学习速度和较高的模型精度,但是SCN 算法依然存在如下的问题:

问题.随着隐含层节点数目的增加,SCN 算法可能存在过拟合和泛化性能差的问题.由于隐含层节点的增加,使得模型学习时结构较复杂,致使模型对已知训练数据表现较好,而对未知数据具有较差的测试效果,造成过拟合的问题.由于过拟合的存在,使得模型鲁棒性不足、泛化能力差,难以实际应用.

另外,PLC 控制系统已广泛应用于主通风机切换过程[14].由于受PLC 存储空间、运行效率等的限制,需要建立一个先进的小尺寸网络来减轻计算和存储压力.因此有必要建立高质量、小尺寸的井下供给风量估计模型.

针对上述问题,在SCN 算法的基础上,结合正则化(Regularization,R)技术,本文提出一种新型的改进SCN 算法,即RSC 算法.该算法包含两个版本:RSC-I 和RSC-II.两个版本的算法在相同的不等式约束条件下随机分配隐性参数,但采用不同的方式计算输出权重.RSC-I 算法通过求解局部正则化最小二乘问题来确定输出权重,而RSC-II 算法采用全局正则化最小二乘法计算输出权重.基准回归分析和工业实验表明:相比SCN 算法,本文方法不仅具有较高的建模精度和较好的泛化能力,而且还减轻了PLC 存储和计算的压力.

1 主通风机切换过程与特性分析

1.1 主通风机切换过程及井下供给风量建模的必要性

主通风机切换过程如图1 所示,由两大动力源的过渡、4 个风门的切换2 部分组成.假设当前工作主通风机为一号主通风机,备用主通风机为二号主通风机,那么一号主通风机、完全关闭的一号水平风门与二号垂直风门、完全打开的一号垂直风门和地下矿井共同构成一个典型的矿井通风系统.主通风机切换过程就是切断一号主通风机与地下矿井的连接,同时建立二号主通风机与地下矿井的连接.矿井通常采用的主通风机切换过程可描述如下:首先,启动二号主通风机,再打开二号垂直风门和一号水平风门;同时,关闭二号水平风门和一号垂直风门;最后,直到4 个风门完全到位后,才关闭一号主通风机.

图1 主通风机切换过程示意图Fig.1 Diagram of a main fan switchover process

主通风机切换时,井下供给风量是由两台主通风机共同提供的,同时又受井下工作环境的影响,对实现主通风机切换过程闭环优化控制起着重要作用.井下供给风量不仅是表征能耗水平和运行状况的重要指标,而且决定地下矿井工作环境质量、采煤效率和矿井安全生产.目前,国内外对主通风机切换过程闭环控制和运行优化的研究较少[15-17],并且这些研究成果严重依赖井下供给风量的实时测量.但是在实际应用中,由于井下供给风流含有成分复杂的气、液、固三相混合杂质,致使取压孔容易发生堵塞,造成风量测量装置的测量效果不理想.因此,对井下供给风量进行有效估计,不仅能为矿井值守人员提供信息来判断主通风机切换过程运行状态和井下工作状况,而且有益于实现井下供给风量的控制和运行优化.

1.2 建模复杂性及特性分析

主通风机切换过程是一个极其复杂的过程.其中,包含气、液、固三相混合杂质的井下供给风流耦合交错,同时井下工作环境极其恶劣;地下矿井局部通风机的启停和井下控制气流的风门状态以及作业人员的变动,运行工况不稳定;各类采矿活动(回采工作面、电池和燃料充电站、矿石破碎站等)中,污染物产生的速度及其质量的变化,运行工况动态时变.这些导致了难以建立准确可靠的主通风机切换过程模型.

表1 列出了主通风机切换过程的相关变量.从图1 可知,影响井下供给风量指标的关键过程变量为:H1d、H2d、R1c、R1s、R2c、R2s、R0.下面对上述7 个变量进行具体地分析.

表1 主通风机切换过程相关变量Table 1 Related variables in the MFSP

1)一号主通风机压头H1d和二号主通风机压头H2d对井下供给风量Q0的影响

对于主通风机,在额定转速下,其风压Hf可描述为主通风机风量Qf的函数.根据该主通风机特性曲线[18],一般将这个函数描述为如下二次多项式:

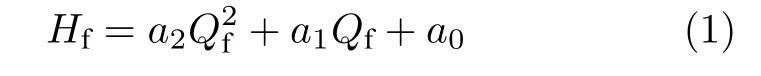
式中,a0,a1和a2为待定常数,根据风机特性曲线进行确定.

根据风机定律[19],转速N所对应的主通风机风压H可以写成:

式中,Nf为额定转速,Q为转速N所对应的主通风机风量.

从式(2)可知,当转速已知时,通过主通风机风压可以得到对应的主通风机风量.因此,对于转速可测的两台主通风机,可得:

式中,f1(·) 和f2(·) 为确定的非线性函数.

根据基尔霍夫风流定律[20],从图1 可得:

由式(3),(4)和式(5)可知,H1d的变化会引起Q1c的变化;同时当H2d发生变化时,Q2c也将随之发生改变.另外,由式(6)可知,Q0是由Q1c和Q2c共同决定的.因此,H1d和H2d对井下供给风量Q0产生重要影响.

2) 风门支路风门风阻R1c,R1s,R2c和R2s对井下供给风量Q0的影响

由Darcy-Weisbach 方程可知,风道压降与通过风道的风量之间的函数关系是非线性的[2].根据文献[21-22],可将这个函数关系写成:

式中,Hic和His分别为主通风机垂直风门和水平风门压降,i为主通风机.

由于Hic和His可看作i号主通风机的负载,因此它们是由Hid提供的.另外,由式(7)可知,风量和风阻之间呈现非线性关系.那么上式可写成:

式中,η(·) 为非线性函数.

由式(4),(5)和式(8)可知,风门风阻R1s,R1c,R2c和R2s是影响风量Q1s,Q1c,Q2c和Q2s的重要因素.再结合式(6)可知,上述风阻是影响井下供给风量Q0的关键过程变量.

3)井下风阻R0对井下供给风量Q0的影响

对于地下矿井,压降H0与风阻R0之间呈现出明显的非线性特征.用公式描述为:

H0可视为两台主通风机的负载,其数值由H1d和H2d共同决定.主通风机切换过程中,R0是不需要进行调节的,但会受到一些因素的影响.例如,井下工作人员的变动,井下控制气流的风门状态,井下作业状况等.上述这些因素都会引起R0的变化.根据式(9) 可知,R0的变化会引起井下供给风量Q0的改变.

综上所述,将主通风机压头H1d和H2d、风门风阻R1s,R1c,R2c和R2s、井下风阻R0作为建模输入变量,就可以实现井下供给风量Q0的估计.这个非线性映射可描述为:

式中,φ(·) 为未知的非线性函数.

2 相关算法

2.1 随机配置网络

SCN 开始于一个小尺寸的SLFNN,首先在一个不等式约束条件下,逐个选取隐含层节点,同时自适应地选择隐性参数的范围;然后,利用全局最小二乘法确定当前网络的输出权重;最后,直到达到设定的最大隐含层节点数目或期望的网络精度时结束隐含层节点的增加.

令 Γ :={g1,g2,g3,···} 表示一组实值函数,span(Γ)表示 Γ 张成的函数空间;令L2(D) 表示定义在D⊂Rd上 的所有勒贝格可测函数f=[f1,f2,···,fm]:Rd→Rm的空间.

给定一个目标函数f:Rd→Rm,假设存在一个建立好的带有L－1 个隐含层节点的SLFNN,那么SLFNN 的输出可表示为:

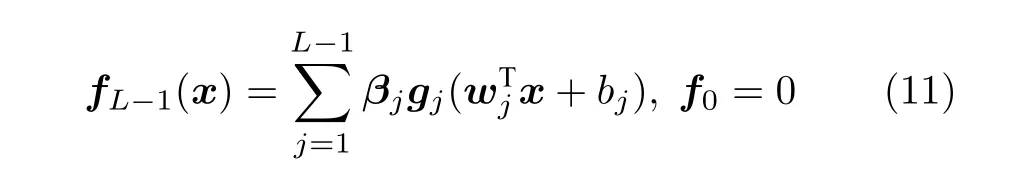
式中,L=1,2,···,wj和bj分别为第j个隐含层节点的输入权值和偏置,βj=[βj1,βj2,···,βjm]T为连接第j个隐含层节点与输出层节点的输出权值,gj为第j个隐含层节点的激活函数.

根据式(11),可以得到当前网络残差eL-1:

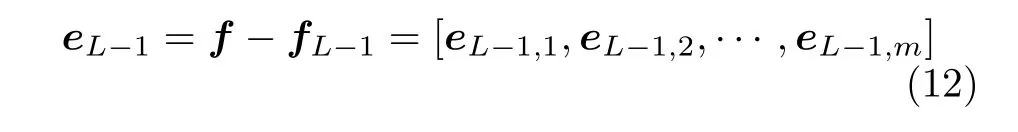
SCN 算法构造一个不等式约束条件来增加第L个隐含层节点,其不等式约束的形式如下:

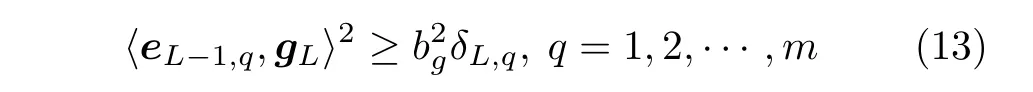
式中,∀g∈Γ,bg∈R+,使得0＜||g||＜bg成立,δL的形式为:

式中,0＜r＜1,uL满足 l imL→+∞uL=0 和0＜uL≤(1－r).

SCN 中表现最好的SCN-III 算法采用全局最小二乘法来计算输出权重:

SCN 中表现最好的SCN-III 算法采用上述方式进行隐含层节点的逐个增加,直到满足设定的条件.

2.2 正则化随机权神经网络

与标准随机权神经网络(Random vector functional-link networks,RVFLNs) 相比,正则化RVFLNs 不仅能有效避免过拟合问题,而且能通过减小输出权重来降低模型复杂性.

式中,ϵi为网络残差,C为正则化系数.通过正则化最小二乘法直接计算输出权重β,具体结果如下:

式中,H=[g1,g2,···,gL],Y=[t1,t2,···,tN]T.

3 RSC 算法

3.1 RSC 算法的收敛性分析和证明

给定神经网络训练样本 (x,t),其中,x={x1,x2,···,xN},xi=[xi,1,xi,2,···,xi,d]T∈Rd,t={t1,t2,···,tN},ti=[ti,1,ti,2,···,ti,m]T∈Rm,假设已经搭建一个带有L－1 个隐含层节点的SLFNN,那么可以得到当前网络的输出权重:

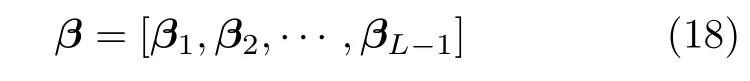
接下来,需要构造一个方案来分配隐性参数,并计算输出权重βL,使得建立的带有L个隐含层节点的SLFNN 具有更高的模型精度.因此,引入如下目标代价函数:

将式(19) 两边同时对βL求导,再结合eL=eL-1－βLgL,可得:

注 1.从式(19)可知,正则化系数C起到平衡的作用,在保证模型精度的同时,降低了复杂度,因此需要对其进行适当选择.本文通过简单的一维搜索程序来确定合适的正则化系数C.从定理 1 可知,对于给定合适的C,RSC 算法不仅保留了SCN 算法收敛速度快的优点,而且能有效地克服过拟合问题.

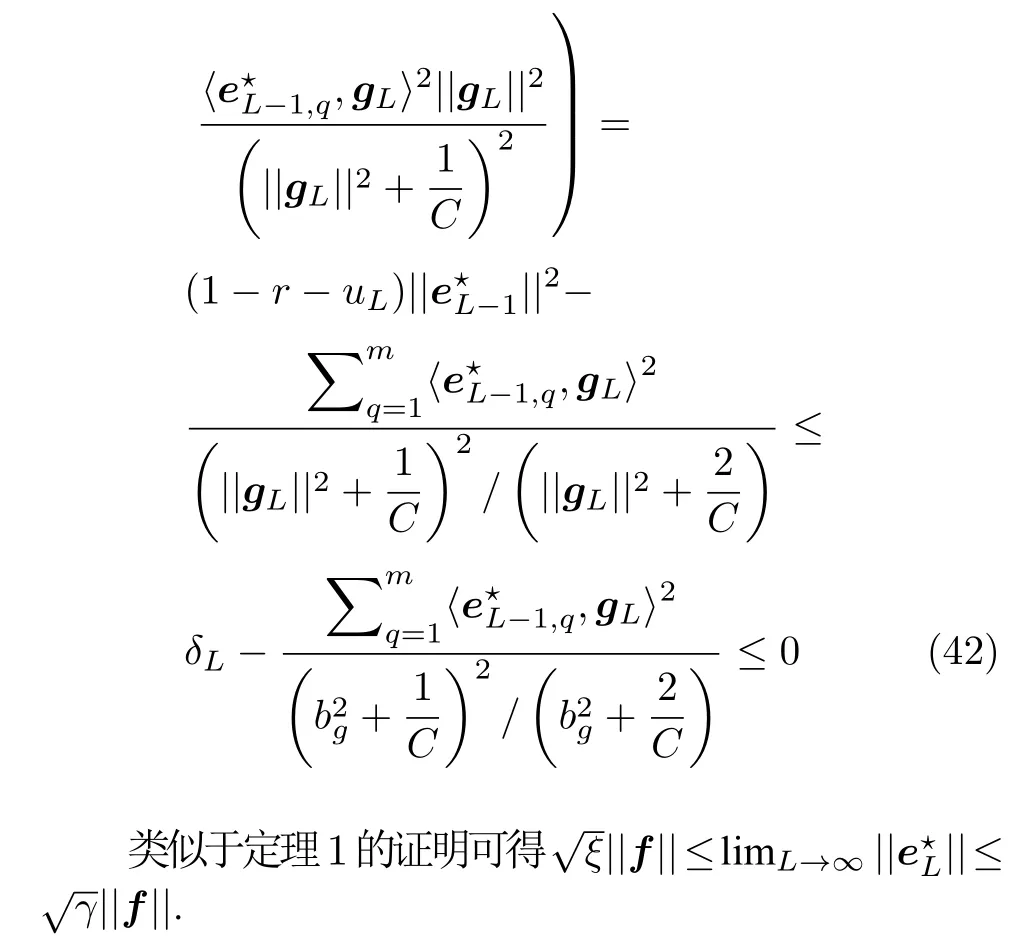
注 2.从式(38)可知,正则化系数C控制和之间的平衡.另外,不等式约束(37)的作用是增大网络残差函数的下降量,从而加快算法的收敛速度.因此,定理2 所对应的RSC 算法不仅能有效抑制过拟合现象,而且具有较快的收敛速度.

3.2 算法描述

定理 1 和定理2 分别对应本文提出的RSC 算法的两个版本,即RSC-I 算法和RSC-II 算法.由于RSC-II 算法比RSC-I 算法具有更快的收敛速度,因此本文着重给出RSC-II 算法的实现步骤.

式中,hL(x) 为第L个隐含层节点输出.那么当前网络的隐含层输出矩阵可写为HL=[h1,h2,···,hL].

为简单起见,引入一组变量ξL,q,q=1,2,···,m.其表达式如下:

RSC-II 算法流程:

给定神经网络的训练样本 (x,t),其中,x={x1,x2,···,xN},xi∈Rd,t={t1,t2,···,tN},ti∈Rm;最大隐含层节点数为Lmax,期望精度为ϵ,随机配置的最大次数为Tmax; 选择一组正的标量Υ={λmin:Δλ:λmax}.

步骤 1.神经网络的初始化阶段:令e0:=[t1,t2,···,tN]T,给定C＞0,一个充分小的正实数ε给定 1－ε＜r＜1,两个空集:Ω andW;

步骤 2.神经网络的训练阶段:随机参数配置和输出权重计算.

当L≤Lmax和||e0||F ＞ϵ时,

随机参数配置:

4 实验分析

为验证所提RSC-II 算法的有效性,与SCNIII[13]算法进行比较分析.为保证实验结果的可靠性,选择一个函数近似、四个基准数据集和一组主通风机切换过程数据作为仿真对象.所有仿真实验在MATLAB 2016a 中进行,使用CPU 为i5,3.4 GHz,内存为8 GB RAM 的PC 机.选择Sigmoid 函数g(x)=1/(1+exp(－x))作为两种算法隐含层节点的激活函数.将神经网络的输入输出数据归一化到区间[0,1].

在一定的噪声水平下对两种算法进行评价.选择均方根误差(Root mean square error,RMSE)作为评价算法泛化能力的指标.每组进行20 次试验,选择20 次试验的平均值(Mean) 和标准差(Standard deviation,STD)作为最终结果.随机参数的最大配置次数为Lmax=200,网络精度取值为ϵ=0.01.其他相关参数的设定将在具体的仿真实验中给出.

4.1 函数近似

考虑一个函数近似[23]问题:

式中,x∈[0,1].

由rand(0,1)随机产生1 000 个数据作为训练样本,由linspace(0,1,300)等间隔生成300 个数据组成测试样本.为验证所提RSC-II 算法能有效克服过拟合问题,需要对训练数据进行预处理,即在训练样本中添加一定比例的异常值.训练样本中异常值的比例为 5 %,其形式为:

式中,yi∈[0,1] 为归一化训练样本的第i个输出,i从 [1,2,···,N] 中随机选取,r and(0,1) 为 (0,1) 之间的随机数.

由式 (37) 和式(38)可知,正则化系数C严重影响算法的学习精度,C的选择可以提高精度,也可以降低精度.为显示C对网络性能的影响,针对不同的C,对RSC-II 算法进行仿真.C在集合{2-20,2-19,···,20,···,219,220}中依次取值,一共有41个数值.同时设定λmin=100,Δλ=1,Lmax=50.从图2 可以看出,C越小,RSC-II 算法的训练能力越差,对测试能力亦是如此.当C大于20时,与SCN-III 算法相比,RSC-II 算法显示出更好的测试性能.另外,对于一个合适的正则化系数C,在相同的训练精度下,RSC-II 算法比SCN-III 算法具有更高的测试精度.因此,在建立网络时,需要确定合适的系数C.那么在下面的仿真实验中,RSC-II 算法使用合适的正则化系数C.

图2 不同 C 下RSC-II 和SCN-III 算法对函数近似的训练与测试精度结果对比Fig.2 The result comparison of training and testing accuracy of RSC-II and SCN-III on function approximation with varying C

图3 (a)为包含 5 % 异常值的1 000 个训练样本,图3 (b)为两种算法对测试数据集的测试性能.可以看出,相比于SCN-III 算法,RSC-II 算法具有更好的拟合能力.从图4 可知,RSC-II 算法总是获得比SCN-III 算法更低的测试RMSE.随着隐含层节点数目的增加,RSC-II 的泛化能力得到提高或者基本保持不变,而SCN-III 的性能变差.这是因为SCN-III 算法始终存在过拟合问题,并且随着隐含层节点的增加,过拟合问题更加严重.RSC-II 算法通过引入正则化系数用于平衡近似精度和模型复杂度,可有效避免过拟合问题.表2 给出了两种算法的具体实验结果.

表2 函数近似的性能比较Table 2 Performance comparisons on the function approximation

图3 (a)包含5 %异常值的1 000 个函数近似训练样本和目标函数;(b)两种算法对测试数据的近似性能Fig.3 (a) 1 000 training samples containing 5 % outliers for function approximation and target function;(b) Approximation performance on the test dataset by two learning algorithms

图4 平均两种算法在测试数据集上的测试RMSEFig.4 Average testing RMSE of the two algorithms on the test dataset

4.2 基准数据

为进一步验证所提RSC-II 算法的有效性,选取UCI 数据库[24]中的四个数据集进行实验.相关数据集的信息和参数设置如表3 所示.采用类似于函数近似问题中的策略进行训练数据预处理.首先,从归一化训练数据中随机选取 5 % 的样本;然后,通过式 (47) 对选中的数据进行预处理.

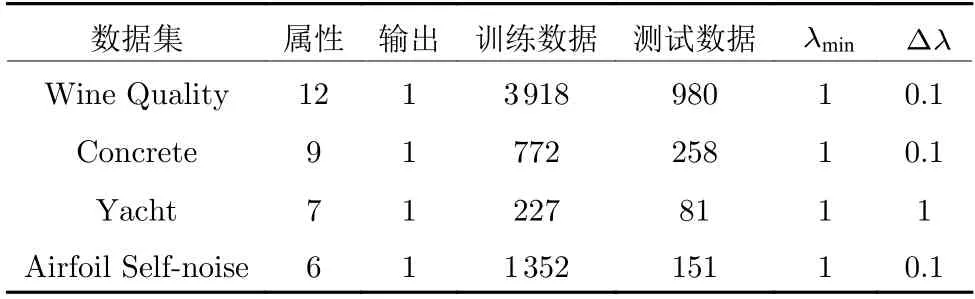
表3 回归数据集与参数设置Table 3 Specifications of benchmark problems and some parameter settings

从图5 可以看出,随着隐含层节点数的增加,SCN-III 算法的测试集RMSE 呈现明显上升趋势,而RSC-II 算法的测试集RMSE 趋于平稳,因此SCN-III 算法出现过拟合现象,而RSC-II 算法未出现过拟合问题.这是因为随着隐含层节点数的增加,神经网络结构变得过于复杂,使得SCN-III 算法出现过拟合问题,对测试数据表现较差.由于RSCIII 算法引入的正则化系数C起到了平衡模型复杂度与拟合精度的作用,避免了过拟合问题,对测试数据具有较好的测试效果.两种算法的具体实验结果如表4 所示,其中,(a)、(b)、(c)、(d)分别为Wine Quality、Concrete、Yacht、Airfoil Self-noise 数据集.

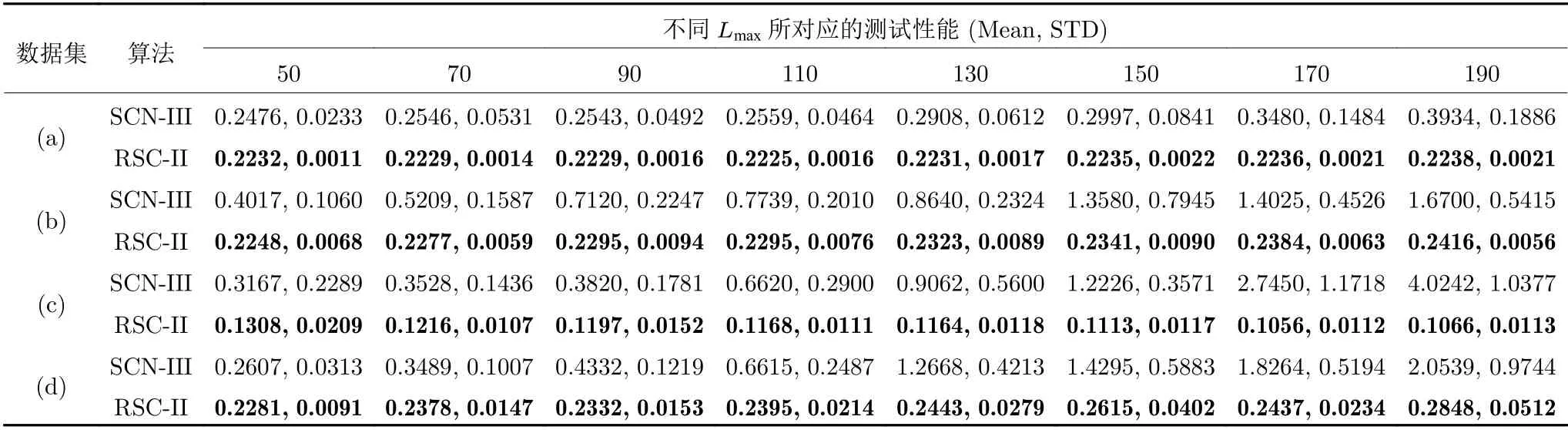
表4 对基准数据集的性能对比Table 4 Performance comparisons on benchmark datasets

图5 不同 Lmax 下RSC-II 和SCN-III 算法对基准数据集的测试RMSE 对比Fig.5 Test RMSE comparison of the RSC-II and SCN-III algorithms on four benchmark datasets with differentLmax

4.3 井下供给风量估计

前面两个小节的实验仿真验证了所提RSC-II算法的有效性,本小节将其在实际主通风机切换过程进行井下供给风量估计.在实际工业现场采集1 500 个样本作为建模的输入输出数据,其中选择1 400 个样本作为训练数据,其余100 个样本作为测试数据.采用前面两个小节中类似的方式对训练数据进行预处理,λmin值设定为1,Δλ也取值为1.

从图6 可以看出,RSC-II 算法的泛化能力始终优于SCN-III 算法的泛化能力.当隐含层节点数为50 时,两种算法的性能比较相近.随着隐含层节点数的增加,RSC-II 算法测试集的RMSE 始终保持在较低的水平,而SCN-III 算法测试集的RMSE 上升趋势明显.因此,相对于RSC-II 算法,SCN-III算法出现了较为明显的过拟合现象.其原因在于当神经网络结构变得尤为复杂时,SCN-III 缺乏应对的能力,从而导致泛化能力差、鲁棒性不足的问题.引入了正则化系数C的RSC-II 算法对模型精度和复杂度进行折中,在保证精度的同时,降低了模型复杂度.表5 列出了两种算法实现的具体实验结果.

表5 在实际MFSP 数据集上的性能对比Table 5 Performance comparisons on the actual MFSP dataset

图6 平均两种算法在实际MFSP 数据集上的测试RMSEFig.6 Average testing RMSE of the two algorithms on the actual MFSP dataset

图7 给出了在Lmax=50 时两种算法的测试性能.可以看出,相比于SCN-III 算法,RSC-II 算法的估计值能很好地拟合实际值,模型精度较高.综上,采用RSC-II 方法建立的井下供给风量估计模型可以以很高的精度对建模数据进行拟合,尤其是可以避免过拟合问题.另外,随着主通风机切换过程样本数据的增多,需要适当地增加隐含层节点数.结果表明,基于RSC-II 的建模算法在隐含层节点数为170 时仍表现出良好的泛化性能和预测精度.因此,本文所提方法能够用于主通风机切换过程实现井下供给风量的建模.

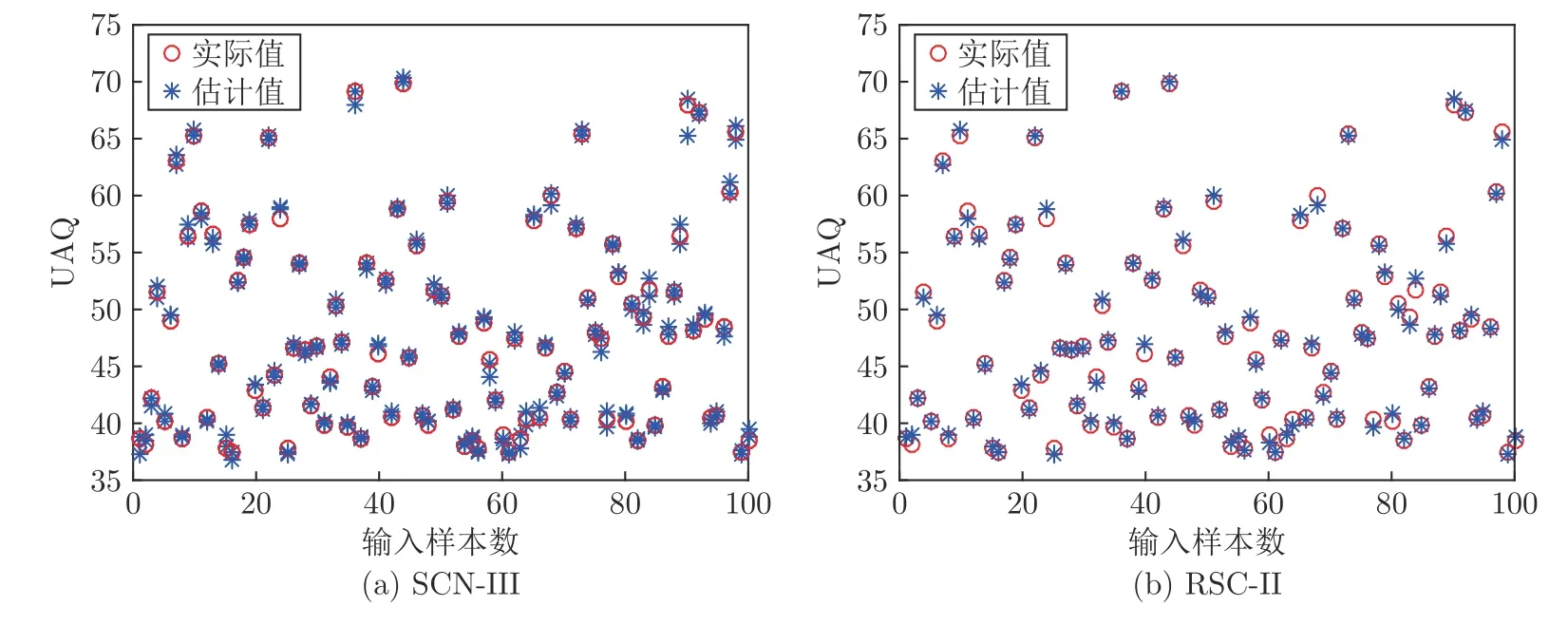
图7 Lmax=50 所对应的MFSP 数据集的测试性能:(a) SCN-III;(b) RSC-IIFig.7 Test performance at Lmax=50 on the actual MFSP dataset:(a) SCN-III;(b) RSC-II

5 结论

针对SCN 算法建模时存在过拟合和泛化能力差的问题,本文结合正则化技术,提出一种新型的RSC 算法,用于建立主通风机切换过程井下供给风量的估计模型.与SCN 算法相比,建立的RSC-II模型不仅具有更高的模型精度,而且具有更好的泛化能力.尤为重要的是RSC-II 算法可以有效避免SCN 算法存在的过拟合问题.同时,RSC-II 算法具有与SCN 算法相同的小尺寸特性.因此,基于所提算法建立的模型具有尺寸小、鲁棒性强、泛化性能好的优点,能够应用到实际主通风机切换过程进行井下供给风量估计.