一种改进的无刷直流电机无位置传感器启动控制策略

李华栋

（陕西东方航空仪表有限责任公司，陕西 西安 710000）

永磁电机以其高效、高功率密度的特点被广泛应用于各种工业自动化及家用电器设备中。按照其反电势波形，永磁电机主要可分为带有正弦波反电势的交流同步电机和带有梯形波反电势的无刷直流电机。对于无刷直流电机（brushless direct current motor，BLDCM），每个电周期仅需六个离散的转子位置信息即可提供与反电势同相的梯形波电流，因此，通常使用低成本的位置传感器（如霍耳式传感器）来进行位置信号获取[1]。

然而，这类传感器也有较为明显的缺点，包括：增加了电机系统成本，需要安装特殊的机械装置；对温度敏感，限制了电机的运行工况；额外的组件和布线降低了系统可靠性。在这种条件下，无位置传感器控制可以从根本上解决这一问题[2-3]。

利用感应的相反电势来估计转子位置是目前BLDCM无位置传感器控制的常用方法，但是，电机在静止时，绕组线圈中并不会感应出反电势，需要启动算法或初始位置检测方法才能实现电机的顺利启动，直到达到反电势信号可稳定使用的最低转速才可进行控制方式的切换[4-5]。

文献[6-8]通过给电机的两相绕组通电来完成初始定位，然后根据给定的激励顺序，通过减小时间间隔的方式使转子加速。针对这种方式，常用的做法是使用斜坡信号在开环模式下进行加速。需要注意的是，斜坡信号的设置参数需要和电机系统的负载相匹配。文献[7]指出，这种方法各相的励磁顺序固定在一个开环中，且激励频率需从一固定值开始，并以一定的速率增加，从而迫使转子跟随。文献[9]对开环启动的缺点做了说明，转子存在不遵循激励顺序的情况，从而导致电机振荡或反向旋转。为了避免这一情况，文献[10]调整了激励频率的上升速率，在一定程度上增强了启动过程的鲁棒性。文献[11]在预定位后采用120°电角度切换模式，随后开始无位置传感器运行，但由于需要检测续流二极管电流，加大了硬件电路设计难度。在文献[12]中，通过测得电压、电流及切换时刻的电流导数定义了一个复合函数，且预定位精度为60°电角度。由于复合函数依赖于电流的微分值，使该方法易受到噪声信号的影响。基于以上分析，现有的BLDCM无位置传感器启动控制通常采用预定位、开环启动模式。此时，绕组的通电次序及PWM占空比均按照固定的速度曲线模式，而此类方法在实验中成功率并不高，外界干扰会造成换向时间不固定，导致通入绕组的激励电压产生反向转矩，使电机反转。

本文提出了一种改进的三段式BLDCM无位置传感器启动控制策略，在检测转子初始位置时确保转子不发生转动，随后采用闭环控制使电机加速到反电势的可检测点，最后通过线电压差值法来判断反电势过零点，完成无位置传感器顺利启动。

1 转子初始位置检测

预定位是BLDCM三段式启动的第一步，对两相绕组进行电压激励后，感应的气隙磁场可以拉动转子到初始指定位置。此后，根据换相逻辑，使绕组按照次序通电，当转速达到自同步状态时，通过检测反电势完成换相运转。文献[11-12]都是按照这种思路使转速达到自同步阶段，这类方法操作简单，但实际操作时，通电后两项绕组合成气隙磁场的方向与转子磁场方向存在重合及相差180°电角度两种可能，则预定位不能一次完成。同时，结合前文相关文献的分析可以看出，在重载或高精度等工况中，这种简单的预定位方式会使电机的转动方向与实际相反，造成启动失败。

根据开关管的导通状态，设定六个空间电压矢量状态U1～U6，依次向两相绕组中通入占空比固定的电压脉冲。由于响应电流值I1～I6的大小会出现变化，这里以I2和I3为例对可能出现的两种情况进行分析：当最大值为I2时，转子N极位于电压矢量U2相邻的±30°范围内，如图1中阴影部分所示；当最大两个电流值为I2及I3时，转子N极位于U2和U3之间的60°范围内，如图2中阴影部分所示。

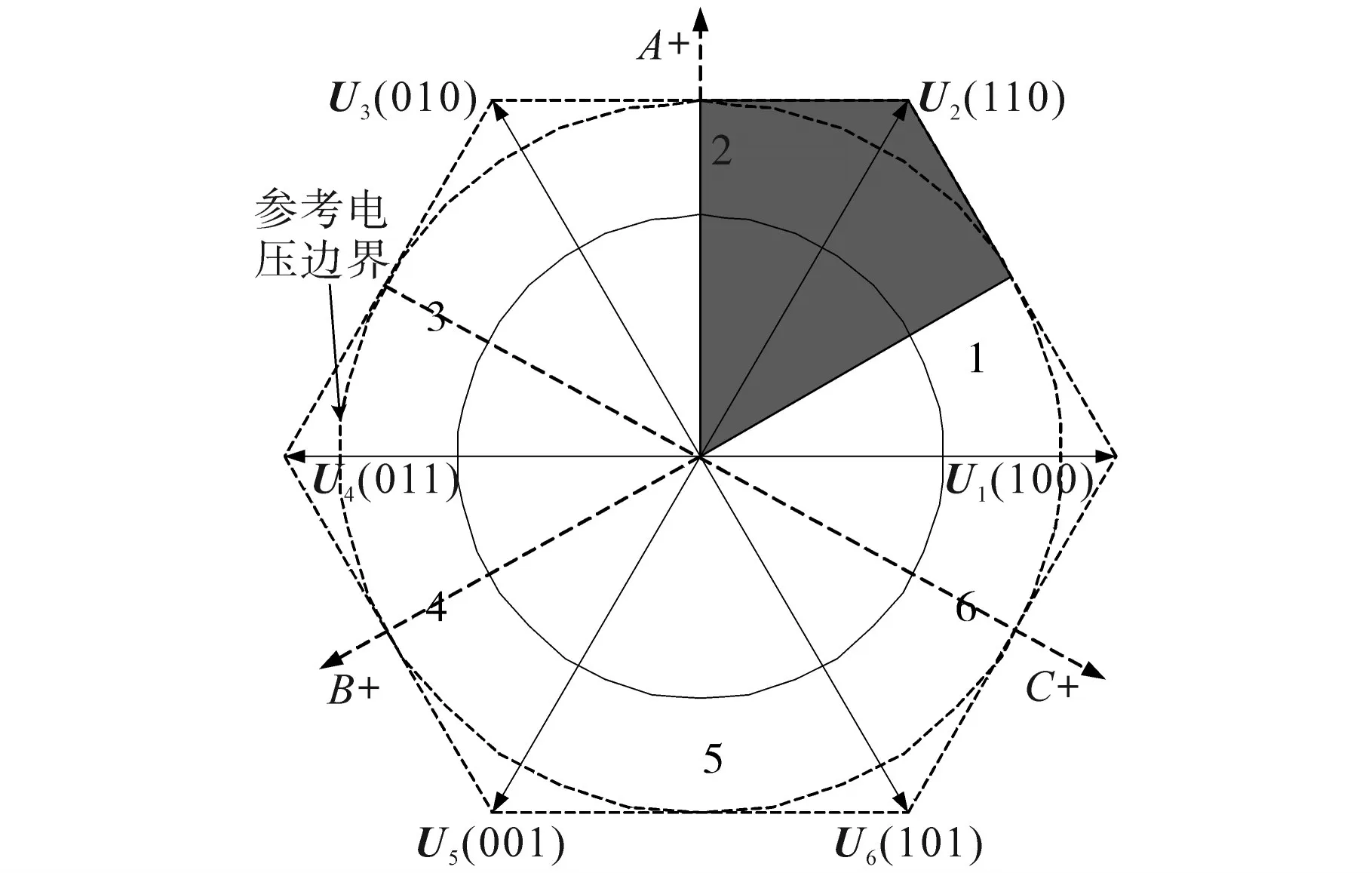
图1 I2为最大值时的转子静止状态定位图Fig.1 The rotor static state positioning when I2is the maximum value

图2 I2及I3为最大值时的转子静止状态定位图Fig.2 The rotor static state positioning when I2and I3both are the maximum value

在I2和I3为最大电流值的情况下，若N极恰好与图2中的A+方向重合，则电压矢量U4与q轴正向一致。此时，施加电压矢量U4可以确保转子有最大启动力矩。若N极位于图2中阴影部分的其他位置，仅需确保预定位精度在60°范围内，施加电压矢量U4同样可以使电机顺利启动。可见，本方法的核心是根据冒泡规则[13]确定响应的最大电流值，从而进一步明确电机启动所需施加的电压矢量。这里，施加预定位电压占空比的原则为：1）响应电流 I1～I6可被检测到；2）施加的电压信号强度不足以使转子转动。因此，针对不同的电驱系统，施加占空比的具体大小需要以这两条原则为参考在实验测试中获得。

2 改进的无位置启动控制策略

2.1 基于换相精度提升的电机加速控制

BLDCM在低速启动后，由于反电势较低，无法检测到有效的反电势过零点。在传统无位置传感器控制中，通常使用给定的开环速度曲线进行加速。在实际运行过程中，外部干扰会使既定的换向时间发生变化，造成电磁转矩反向，令电机启动失败。为了增强这一过渡过程的抗扰动性，避免开环模式的发散现象，本文从提高换相准确性的角度出发，使用两组电压脉冲分别完成电机加速和转子N极位置检测的工作。两组电压脉冲的空间矢量分布如图3所示，其中，U12～U61为新引入的检测电压矢量。这里，以U23为例来分析转子精确换相的条件。首先，U23与开关管T1～T6的对应的状态关系为100101，0代表开关管关断，1代表开关管导通。通过提高这一电压脉冲矢量的作用占空比，可以使转子N极方向到达A+或U56方向，随后再使电压脉冲U34（101001）发生作用，从而可完成预定位过程。其次，在此基础上，通入电压脉冲U34可获得此时的最大响应电流Imax，且其他位置的最大电流亦可按此获取。若加速阶段检测电压脉冲U12～U61对应的响应电流为Iij（I12～I61），其中，i，j=1，2，3，…，6，则可得到如下的响应电流差值表达式：

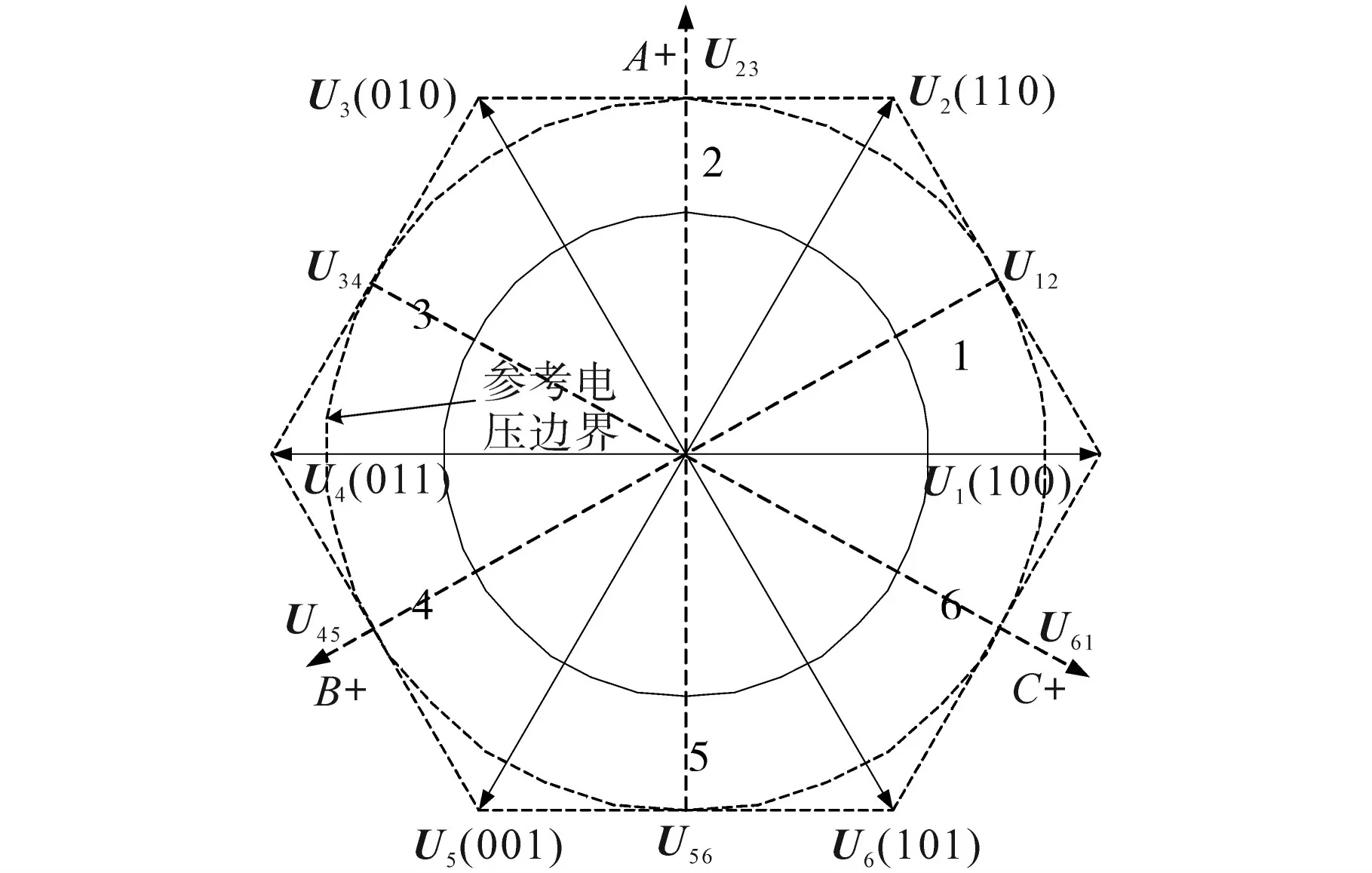
图3 加速阶段电压脉冲矢量分布Fig.3 Voltage pulse vector distribution during acceleration

基于以上分析，随着电机转速继续升高，转子N极开始靠近检测电压脉冲Umax（U34），且响应电流随之增大。当电流差值ΔIij小于换相阈值时，检测电压矢量切换为U45，对应的加速电压矢量切换为U5。按照这一换相原则，可依次得到其他转子位置角的换相逻辑，如表1所示，其中I代表切换阈值。由于始终存在加速和检测电压，转子可以取得最好的转动效果，在保证速度稳定上升的同时使换相精度得到了提高。

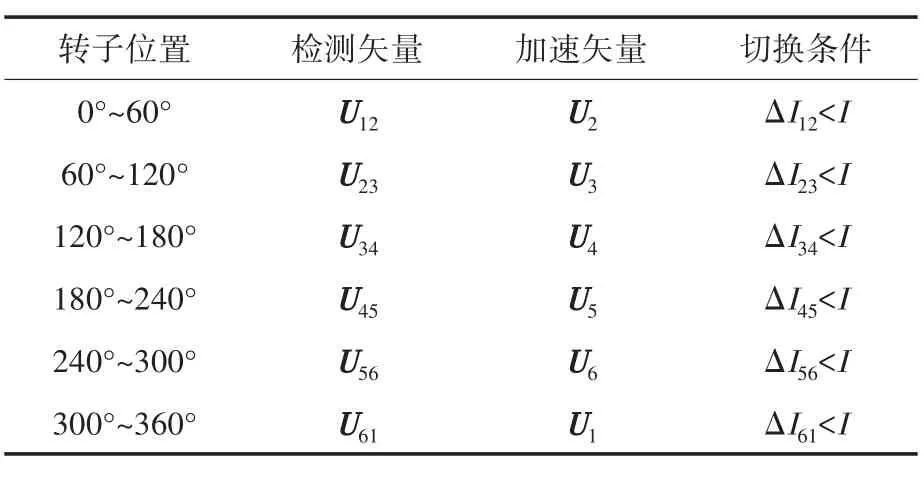
表1 转子位置角换相顺序Tab.1 Commutation sequence of rotor position angle

需要注意的是，针对不同的电机，具体的电流阈值大小也会不同，根据对本系统的实测结果，换相电流阈值可设置为最大值Imax的0.1%～0.5%，本文选择了0.2%，且阈值的设计越小越好，以图3为例，当阈值设计过大时会造成转子N极与U34相距较远时，检测矢量就切换为U45，加速矢量切换为U5，势必出现较大换相误差，造成换相失败。

BLDCM的电机转速方程可表示为

式中：Us为电机端电压；UTD为开关器件管压降；R为相绕组等效电阻；is为电枢电流；KE为反电势系数；Φ为相磁通量；n为电机转速。

由式（2）可知，端电压的变化会引起转速的改变，当n值逐渐增大到反电势可检测点时，可根据换相时刻与过零点的关系完成换相。一方面，通过引入检测电压脉冲完成电机平稳加速，并设置加速区间的速度峰值；另一方面，切换转速不宜过高，否则在切换时会对系统造成较大电流冲击。

在实际的程序执行过程中，通过转速闭环给定使电机运行至转速目标值，这里，BLDCM额定转速为2 500 rad/min，通过实际测试，反电势在转速达到电机额定转速的12%，即300 rad/min时可取得较好的检测效果，此时可通过检测反电势过零点完成换相。

2.2 基于反电势过零点检测的自同步运转阶段

当BLDCM进入无位置传感器自同步运转阶段后，反电势和电流信号的形式如图4所示，当转子N极所在位置δ位于5π/6～7π/6之间时，电流从C相流入，B相流出，且三相电流满足iC=-iB，iA=0。

图4 两相导通下的相反电势和电流波形Fig.4 Back-EMF and current waveforms under two-phase conduction

在iA=0的条件下，A相反电势在过零点相邻30°范围的表达式可被重新写作：

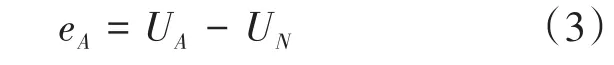
其中

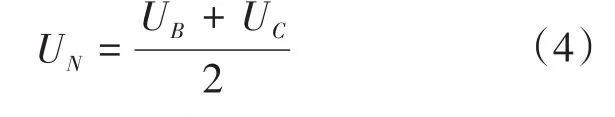
式中：UA为A相电压；UN为中性点电压。

在上述相位区间中，eC=-eB。同理，当转子N极所在位置δ处于3π/2～11π/6或π/6～π/2时，可按照上述方法获得反电势在过零点的eB与eC表达式。

通过传感器测得端电压后，将求得的反电势过零点向后延时30°电角度，即可得到电机的换相位置。为使BLDCM平稳过渡到自同步阶段，还需要对反电势过零点延迟30°电角度的时间进行估算。在图4中，以A相反电势为例，将过零点表示为z，换相点表示为p，则反电势波形在时间轴上会不断出现z点和p点，且时间间隔满足如下关系：

Tzp=Tpz=Tzz/2=Tpp/2 （5）

需要注意的是，在实际应用中，时间间隔的特性并不理想。以本文研究的基于BLDCM拧紧扳手驱动系统为例，电机是瞬间加速的，导致两次换相的时间间隔减小得很快，即Tzp并不等于Tzz的1/2，则按照这一思路计算出的换相时间也是存在误差的。这里，令第n次过零点为z（n），第n+1次换相点为p（n+1），则两者之间30°的延迟时间可表示为Tzp（n）。由于过零点检测会出现偏差，这里结合 Tzp（n）与 Tzz（n）对 n+1 次的换相时间进行修正，可表示如下：

Tzp(n+1)=(Tzp(n)+0.5Tzz(n))/2 （6）

3 硬件执行及实验结果

图5为本文提出的BLDCM无位置传感器启动控制实验框图，主要包括：400 W，2 500 rad/min，1对极的永磁无刷直流电机；可编程电子负载。电机参数如下：定子电阻0.1 Ω，绕组电感0.03e-3H，转子磁链 0.02 Wb，转动惯量3.89e-3kg·m2，额定转速2 500 rad/min，额定转矩12 N·m。

图5 BLDCM无位置传感器启动控制实验框图Fig.5 Experimental block diagram of BLDCM sensorless start control

无位置传感器控制算法在TI TMS320F28335数字信号处理器上执行。驱动电路采用三相IGBT功率模块。通过电阻分压器，电机3个端电压信号的幅值被缩小后送入A/D模块。同时，在执行过程中，通过设置合理的采样方式可滤除换相时续流二极管导通引起的电压尖峰波动。

实验过程包括转子定位、加速及自运行三个部分。首先，在预定位阶段，向电机绕组注入表1所示的电压检测矢量，对响应电流进行对比；当转子进入加速阶段后，采用长、短时脉冲结合的方式进行转子加速，同时检测N极所在的区间位置，在连续检测到稳定的反电势过零点后可切换到同步自运行阶段。具体的实验结果如下。

3.1 实验波形

在实际转子位置为90°时，对初始位置进行检测，依次向两相绕组通入占空比适当的6组电压信号，图6给出了d轴的响应电流对比。

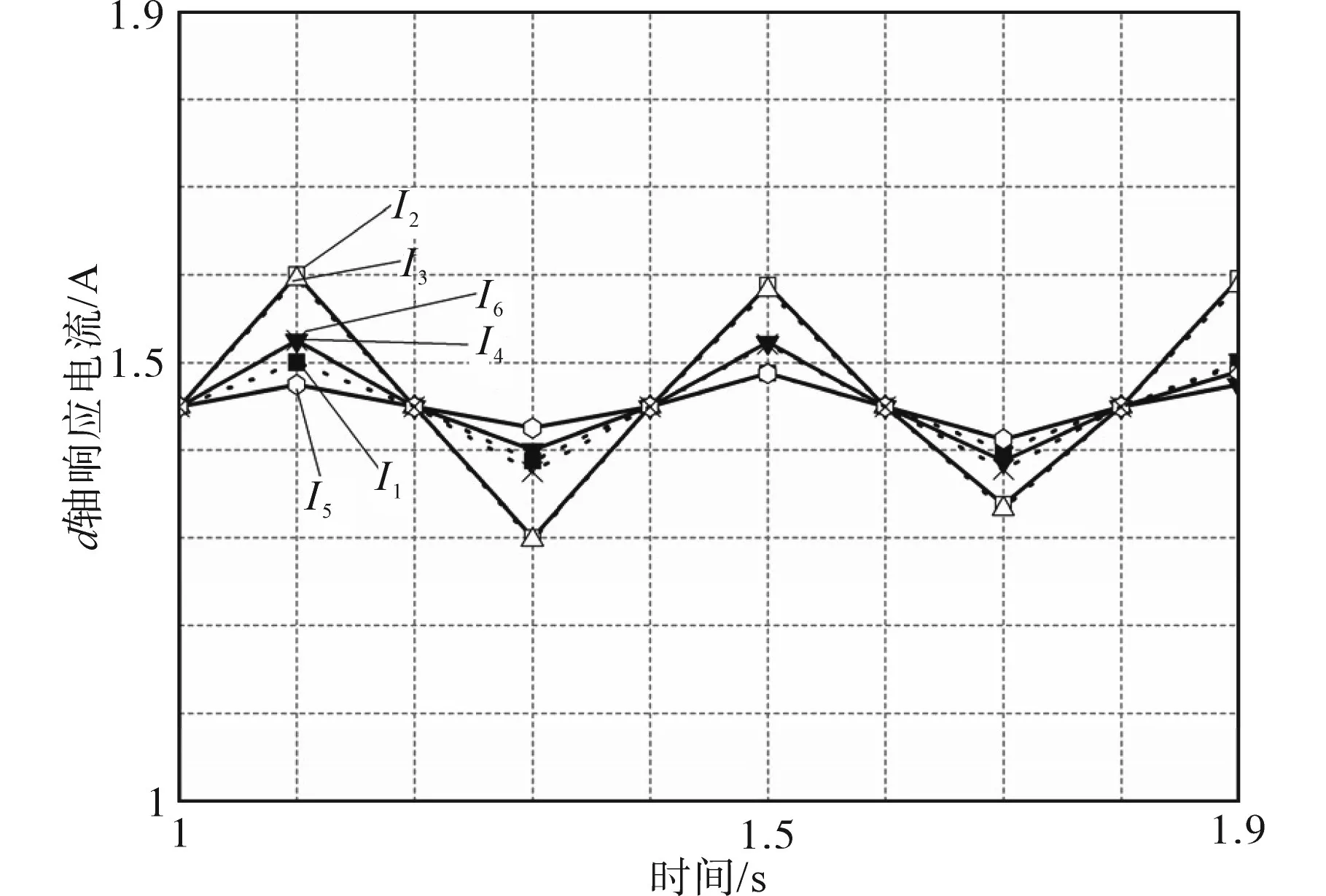
图6 静止实际转子初始位置为90°时的d轴响应电流对比Fig.6 Comparison of d-axis response currents when the actual initial rotor position angle is 90°

在完成初始位置检测后，电机进入加速阶段，目标转速设置为300 rad/min。图7为加速阶段带载5 N·m的部分转子位置估计性能图。图8为相同条件下的转速估计性能图。图9为无位置传感器运行下加速阶段的A相反电势波形。

图7 带载5 N·m加速阶段转子位置估计性能Fig.7 Rotor position estimation performance of acceleration stage when 5 N·m is added

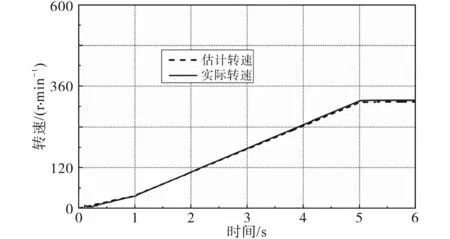
图8 带载5 N·m加速阶段转速（0→300 rad/min）估计性能Fig.8 Speed（0→300 rad/min）estimation performance of acceleration stage when 5 N·m is added

图9 无位置传感器带载5 N·m加速阶段（0→300 rad/min）A相反电势波形Fig.9 Back emf waveform of A-phase with speed（0→300 rad/min）of acceleration stage when 5 N·m is added

当转速达到300 rad/min，无位置传感器控制进入自同步运转阶段。图10为自同步运转稳态2 500 rad/min且带载5 N·m时的A相定子电流波形。图11为无位置传感器控制下转矩的输出波形，其指令值被设置为2 N·m和9 N·m的恒转矩区间，及1～5 s之间对应的3～12 N·m变转矩区间。此外，在实验中，调制方式是在同一时刻对上下桥臂的IGBT均进行控制，为了消除非导通相二极管续流电流的影响，本文采用的具体方式为同一桥臂上下开关器件互补性调制，其导通范围为120°电角度。

图10 无位置传感器转速2 500 rad/min稳态运行时A相电流波形Fig.10 A-phase current at 2 500 rad/min when using sensorless control

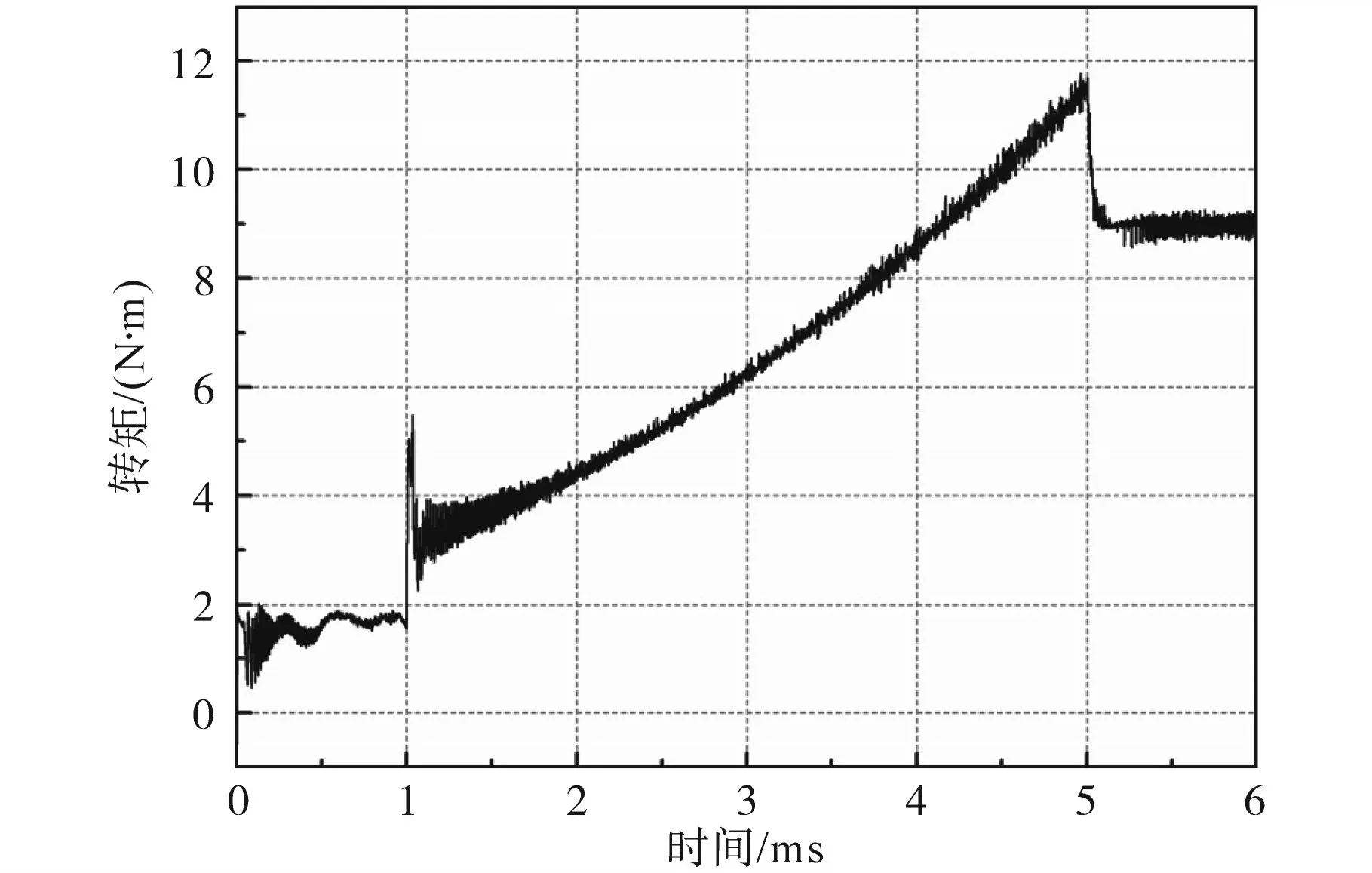
图11 无位置传感器稳态2 500 rad/min负载变化时的转矩波形Fig.11 Torque waveform at 2 500 rad/min when load changes in sensorless control

3.2 实验结果分析

从图6可以看出，当按照图2所示的转子位置进行初始位置检测时，I2和I3的实际d轴响应电流为最大，与图2得出的结论一致。从图7和图8可以看出，在加速阶段，估计的转子位置和转速均可达到较好的跟踪精度，这也意味着BLDCM顺利启动，且启动响应时间能够满足拧紧扳手驱动系统的动态性要求。在初始阶段，估计转速波动较小，且无反转情况出现。由图9中启动过程的反电势波形可以看出，反电势最初的幅值较小，不利于反电势过零时刻的准确判断，而进入自同步稳定状态后，反电势波形清晰稳定，则可以根据线电压差值来确定反电势过零点，从而完成电机的准确换相。

由图10的A相响应电流波形可以看出，在电机高速转动时，电流波形无较大波动，即拧紧扳手在工作时能够保持较好的稳定性，而在算法的实际执行过程中，系统可以根据响应电流值的大小来完成对应的比较环节，从而实现转子的定位和闭环加速。为了评估系统的稳定性，按照图11所示的负载变化在自同步运转阶段施加扰动。显然，输出转矩在扰动条件下也有较快的响应速度。

4 结论

本文针对BLDCM无位置传感器驱动下的启动过程展开研究，提出一种改进的三段式启动控制方法，具体的结论如下：1）在转子预定位阶段，通过控制电压脉冲的占空比大小避免电机出现反转；2）在电机加速阶段引入检测电压矢量，在提升电机转速的同时保证了换相精度；3）当系统状态达到反电势可检测点后，通过对反电势过零点时间进行修正估计，可达到高精度的换相及转子位置、转速估计效果。