基于ARIMA模型预测我国GDP平减指数

李 进

（浙江工商大学金融学院，浙江 杭州 310000）

一、引言

GDP平减指数（GDP Deflator），又称GDP缩减指数，是指名义GDP与真实GDP之比，该指数被广泛用于测度价格水平。对比消费者物价指数（CPI），GDP平减指数考虑本国生产的全部产品和服务，只反映国内生产产品价格变动对价格水平的影响，且计算时对价格的加总方式更加合理。因此，GDP平减指数可以更真实的反映国家物价水平，研究该指数可以更合理的测度宏观价格水平变动。

在20世纪70年代创立的ARMA模型（Autoregressive Moving Average Model，自回归滑动平均模型）在时间序列的预测方面运用甚广，但是使用ARMA模型的前提条件是分析的序列必须为平稳序列。基于差分运算的确定性信息提取能力，许多非平稳时间序列在差分后会显示出平稳序列的性质，因此Box和Jenkins将差分运算与ARMA模型组合后就衍生了ARIMA模 型（Autoregressive Integrated Moving Average Model，求和自回归滑动平均模型），ARIMA模型在时间序列预测方面的应用更为广泛。本文截取1978年至2017年我国的GDP平减指数信息作为时间序列训练集，截取2018年至2020年我国的GDP平减指数作为测试集，建立ARIMA模型。使用拟合的模型预测未来三期数据，并与测试集中的真实数据进行对比，分析ARIMA模型的实际预测效果。

二、ARIMA模型

1.ARMA模型

ARMA（p， q）模型一般表示为：

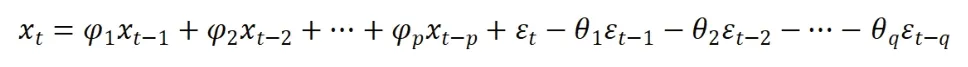
其具体的数学表达式为：

引进延迟算子，ARMA（p， q）模型可以简记为：

2.ARIMA模型

结合差分运算和ARMA模型，具有以下表达形式的模型被称为求和自回归滑动平均模型（Autoregressive Integrated Moving Average Model），简记为ARIMA（p， d， q）模型：

三、ARIMA模型建模过程

本文采用以下建模过程：获取GDP平减指数数据构建时间序列，对构建的时间序列进行平稳性检验，如果检验结果显示序列平稳，则继续对序列进行白噪声检验；若结果显示序列不平稳，则对序列进行差分运算，再重新检验差分后序列的平稳性。若序列通过白噪声检验，则说明序列中没有值得提取的可用信息，建模结束；若白噪声检验提示序列非白噪声，则对序列采用ARMA模型建模（如图1）。

图1 ARIMA模型建模过程

如果原序列或经差分运算后得到的新序列被验证为平稳非白噪声序列，则对其采用如下的过程进行ARMA建模：首先计算自相关系数（ACF）和偏自相关系数（PACF），结合ACF图、PACF图的拖尾、截尾性质以及最小AIC准则为ARMA模型定阶，之后估计模型的相关参数，再对拟合的ARMA模型进行模型检验。如果未通过模型检验，则对模型重新定阶并重新估计参数；如果通过模型检验，则对模型优化后完成ARMA模型构建过程（如图2）。

图2 ARMA模型建模过程

1.数据选取

截取1978年至2020年我国的GDP平减指数信息，数据来源为同花顺iFinD数据库（指标名称：“GDP：平减指数”；频率：“年”；1978=100）。采用R软件，建立GDP平减指数的时间序列，并绘制时序图（如图3），时序图显示观察值序列显然不平稳，应进行差分运算。

图3 GDP平减指数时序图

2.差分运算并在差分后检验序列平稳性

加载R软件中的“aTSA”包。对序列进行一阶差分运算后，通过adf.test（）函数对差分后的序列进行ADF检验，结果显示无漂移项无时间趋势、有漂移项无时间趋势、有漂移项有时间趋势三种情况的P值。在无漂移项无时间趋势下滞后0阶、1阶，有漂移项无时间趋势下滞后0阶、1阶、3阶，有漂移项有时间趋势下滞后2阶，在以上几种情况下，P值都小于α＝0.05的置信水平。综合考虑，可以认为原序列在一阶差分后实现了平稳（如图4）。

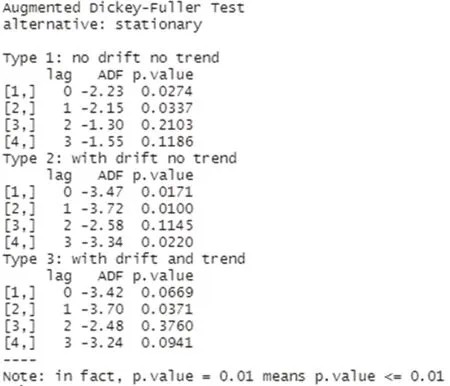
图4 ADF检验结果

3.差分后序列纯随机性检验

构建LB统计量对差分后的序列进行白噪声检验，R语言中使用Box.test（）函数进行序列的白噪声检验，检验的原假设为：H0：序列是白噪声序列。结果显示，在6阶和12阶延迟下LB统计量的P值均小于α=0.05的显著性水平，应拒绝原假设，说明差分后的序列不是白噪声序列。因此可以对差分后的序列拟合ARMA模型（如图5）。

图5 白噪声检验结果

4.绘制序列自相关图和偏自相关图为ARIMA模型定阶

样本自相关图显示1阶显著不为0，2阶之后近似为0；偏自相关图显示4阶之后近似为0，因此可以在1至4之间选择p，q的具体取值（如图6）。

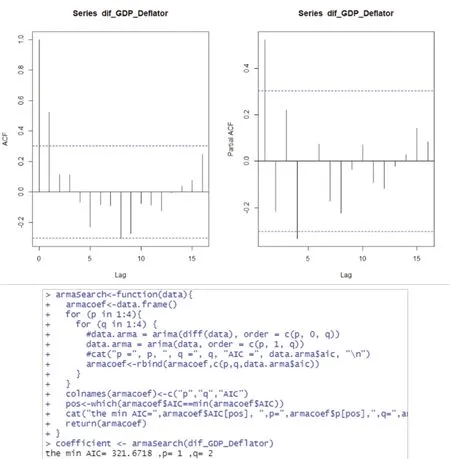
图6 自相关图（左上）、偏自相关图（右上）及最小 AIC 准则定阶结果

R语言中的arima（）函数的输出结果包含AIC值，因此可以通过编写R的循环迭代函数分别计算ARIMA（1， 1， 1）、ARIMA（1， 1， 2）、ARIMA（1， 1， 3）、ARIMA（1， 1， 4）、……、ARIMA（4， 1， 1）、ARIMA（4， 1， 2）、ARIMA（4， 1， 3）、ARIMA（4，1， 4）等16个模型的AIC值并输出最小AIC所对应的p， q值。最终确定最优的系数为p=1，q=2，即对序列建立ARIMA（1， 1，2）模型。

5.建立ARIMA（1， 1， 2）模型

根据定阶结果，调用R语言“forecast”包中的Arima（）函数，拟合带漂移项的ARIMA（1， 1， 2）模型，估计模型中的各参数结果如图 7。

图7 带漂移项ARIMA（1，1，2）模型参数拟合结果

因此ARIMA（1， 1， 2）模型的拟合结果为：

再使用tsdiag（）函数对该ARIMA（1， 1， 2）模型进行显著性检验，tsdiag（）函数会输出模型的残差序列时序图、残差序列自相关图和残差序列的白噪声检验图（如图8）。残差序列的白噪声检验图显示，各阶延迟下白噪声检验统计量的P值都显著大于0.05（图中虚线为0.05参考线），该ARIMA（1， 1，2）模型显著成立。

图8 带漂移项模型残差序列的时序图（上）、自相关图（中）及白噪声检验图（下）

考虑不带漂移项建模的情况，重复以上建模过程。不带漂移项建立的ARIMA（1， 1， 2）模型的残差序列的白噪声检验图显示，在各阶延迟下白噪声检验统计量的P值不能显著大于0.05，也即应该拒绝残差序列为白噪声的原假设，认为残差序列不是白噪声序列，还存在值得提取的信息。因此不带漂移项的ARIMA（1， 1， 2）模型不显著成立，最终选择带漂移项的模型为拟合结果：

四、ARIMA模型预测

基于拟合的ARIMA（1， 1， 2）模型，选择1978年至2017年的GDP平减指数为训练集，选择2018年至2020年的GDP平减指数为测试集，对序列进行未来3期的预测，并将预测结果与测试集中的真实值进行比较，计算预测误差（如图9）。再继续建立未来10期的预测（2021年至2030年），共同绘制模型预测效果图（如图10）。在预测效果图中，实线是序列观察值，虚线是模型拟合值，深色阴影是序列的80%置信空间，浅色阴影是序列的95%置信区间。从结果来看，我国的GDP平减指数存在走高的趋势，也即反映出了我国的物价水平预期会上涨，这与我国经济不断发展的国情以及通货膨胀等经济学原理相契合，符合预期，可以通过经济学检验。基于预测误差、预测效果图以及经济学判断，可以认为该ARIMA（1， 1， 2）模型的拟合与预测效果都不错，可以通过检验。

图9 未来三期预测值、真实值及预测误差

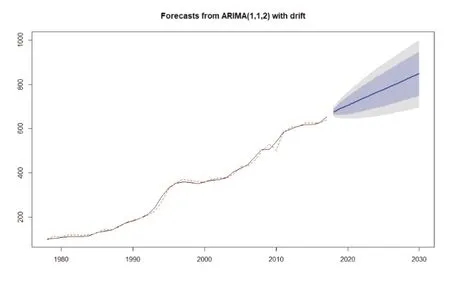
图10 模型预测效果图

五、研究结论

从模型预测效果图可以看出，未来10年的GDP平减指数预计将会持续上涨。虽然ARIMA模型通常只在短期预测中有较高的精确度，随着时间跨度的增大其准确率会不断降低，但即使采用预测值95%置信区间的下限（图中灰色区域的下缘），我国GDP平减指数估计仍然会增大，我国的物价水平预计会不断上涨。这也意味着我国大概率会保持温和的通货膨胀以及稳定的经济发展。

六、结语

本文基于ARIMA模型，以R语言为分析软件，对我国GDP平减指数序列进行时间序列建模。整体思路为：首先选取GDP平减指数数据构建时间序列，然后对该序列进行平稳性检验，在序列不平稳的基础上进行一阶差分得到平稳序列。在序列非白噪声的基础上通过序列的自相关系数、偏自相关系数和最小AIC准则确定模型的滞后阶数。最后用R语言估计模型的未知参数，用拟合的ARIMA（1， 1， 2）模型对未来3期的GDP平减指数进行预测，并与真实值对比验证模型的可靠性。

综上，利用ARIMA模型可以在短期很好的预测GDP平减指数的走向，得到的预测值比较理想，同时拟合的模型也符合经济学原理检验。为学者监测宏观经济指标和了解我国物价水平、经济发展走势提供了一定的参考。