一种腿轮结合的助行器设计及仿真
马 可,李孟员,苑明海,裴自卿
(1.河海大学 机电工程学院,江苏 常州 213022;2.江苏省特种机器人技术重点实验室,江苏 常州 213022)
0 引 言
目前,由于中国逐渐进入老龄化社会,老年性疾病及车祸、扭伤等意外事故而引起的肢体运动性障碍患者明显增加[1-2],下肢运动功能出现问题是影响人类正常行走的一个重要因素,受到了越来越多的关注。下肢康复助行器作为一种辅助老年人和残疾人行走的设备[3],有着巨大的应用前景,经过一段时间的有效康复训练,它可以为因年迈肌力衰退导致行走功能障碍的老年人提供助力,树立起独自行走的信心,改善行走过程中存在的问题[4]。
康复机器人的研究兴起于20世纪80年代的英国,1987年Mike Topping公司研制的Handy-1康复机器人最早实现了康复机器人的商业化[5]。近年来,在国外,Calin Vaida设计了一种机器人系统,可用于在治疗的急性期对卧床受限患者的下肢中风后康复[6];Fereydooni等研究了小波神经网络下肢康复机器人自适应控制中的应用[7];Werner Christian等评估了患有运动障碍的老年人的智能助行器的坐姿到站姿辅助功能[8];Zakharov则对虚拟现实与触觉反馈相结合的中风影响下肢康复进行了研究[9]。
在国内,贾丙琪等在TRIZ的理论基础上对下肢外骨骼进行了创新设计[10];肖丹设计了一款适合下肢功能中、轻度障碍人群的步行辅助装置[11],用以弥补行动障碍;常镭民[12]根据成年人体数据对人体腿部模型建模并进行动力学分析,得到了一种与正常人行走角度曲线大致重合的助行器;还有学者提出了机器人姿态[13]和双足机器人步态规划方案[14];黄锦婷提出了一种可穿戴式下肢康复机器人设计方案[15]。
已有的助行器虽各有所长,但仍然存在使用时需反复抬起而造成的费时费力,以及爬坡能力弱、平稳性较差等问题。因此,文中拟设计一种腿轮结合的下肢康复助行器,充分利用腿、轮各自具备的结构及行走优势,克服现有助行器存在的缺陷。
1 助行器的结构设计
下肢康复助行器是为了帮助下肢行动能力差,但上肢功能健全的老年人或残疾人,使用者可以借助上肢力量站立起来,凭借助行器的动力使其行走能力得到有效的锻炼。文中设计的助行器,采用前腿后轮的设计思路,总体结构如图1所示,主要由运动杆件、传动系统、调速装置、支撑杆件、主体框架等五个部分构成,其中传动系统由电动机、减速器、传动齿轮、传动轴、同步带、阶梯轴等组成。

1运动杆件 21 电动机 22减速器 23传动齿轮 24传动轴 25同步带 26阶梯轴 3调速装置 4支撑杆件 5主体框架
支撑杆件由伸缩杆和臂托组成,主要起到支撑人体的作用。调速装置采用霍尔调速握把实现无级调速。各运动杆件之间通过销轴、开口销连接,降低表面磨损,便于拆卸。传动系统中轴与框架之间都通过滚动轴承连接,减小摩擦。两轴之间通过同步轮与同步带连接,使运动过程平稳且噪音小。
在主体框架内侧设置有传动系统,考虑到能够更加容易的控制,将助行器左右两侧的运动机构通过传动主轴及同步带轮等部件联系到一起,只用一个电机提供输出,同步带,将转矩传递至主轴,再由主轴将转矩传递至两侧行走部件,在安装时注意两侧行走部件的位置关系,利用传动比精确的特点使两侧保持恒定的位置关系。
该下肢康复助行器传动系统的运动结构简图如图2所示。
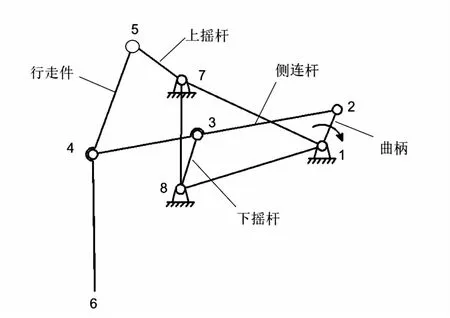
图2 系统运动结构简图
依据公式:
F=3N-2PL-PH
(1)
其中,N为活动构件数,PL为低副数,PH为高副数。
代入本机构数据:
N=5,PL=7,PH=0
计算可得自由度:
F=1
因此,本机构只需要一个原动件就可以有确定的运动状态,由此可知助行器只需一个电动机作为驱动原件即可,避免了使用者需要手动反复抬起的繁琐过程,操作更加简单方便。
助行器工作时,通过将调速握把转动不同角度实现电机不同转速,从而带动主轴转动,主轴通过同步齿形带带动两侧曲柄旋转,于是两侧的运动部件呈现规律的周期性运动,行走件底部安装有脚垫,用以增大与地面的接触面积,从而增大与地面的摩擦力,在运动时利用与地面的静摩擦力带动后轮向前运动,由于腿部杆件有向前迈进的动作,当在不平坦的地面上行走时遇到一定高度的障碍物时可以直接越过。
2 助行器各主要参数的确定
为使此助行器在使用过程中与人体协调一致,需在其正常运动的前提下对各构件尺寸进行合理设计。以一般成年人身高为参考,取助行器除扶手部分整个运动机构顶部至地面高度范围为389 mm~439 mm,以达到提供给使用者休息时坐立的最佳状态。确定了整体高度之后,结合该器械的运动特点,确定各杆件长度,结果如表1所示。
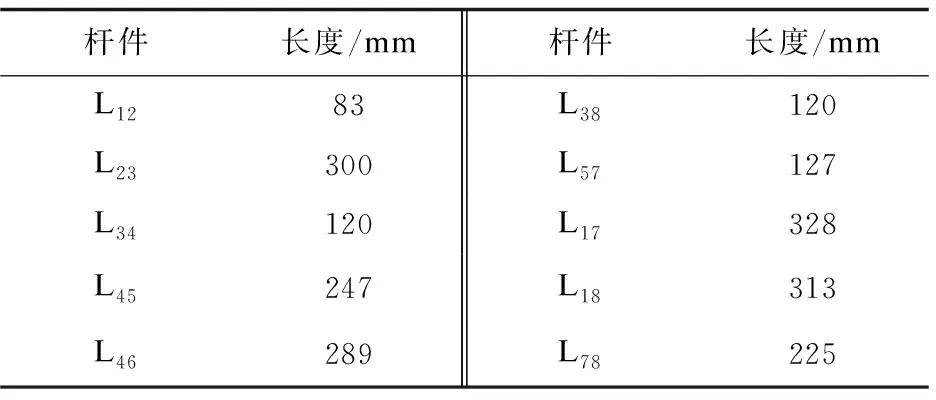
表1 各杆件尺寸数据
考虑到助行器主体重量不宜太大,故应当在满足强度要求的前提下尽量减小材料密度,样机材料最终选定6061铝合金,计算可得各杆件质量分别为:行走件:1.34 kg;上摇杆:0.11 kg;下摇杆:0.12 kg;侧连杆:0.82 kg;曲柄:0.08 kg。
3 腿部杆件运动分析
在确定了各杆件尺寸及材料后,需要对该助行器的运动状态进行分析,一方面通过计算得出其运动的步距,为电机参数的选择和速度的设定提供参考;另一方面,计算出该助行器运动过程中起伏状态,可以对其运动的平稳性做出评估。
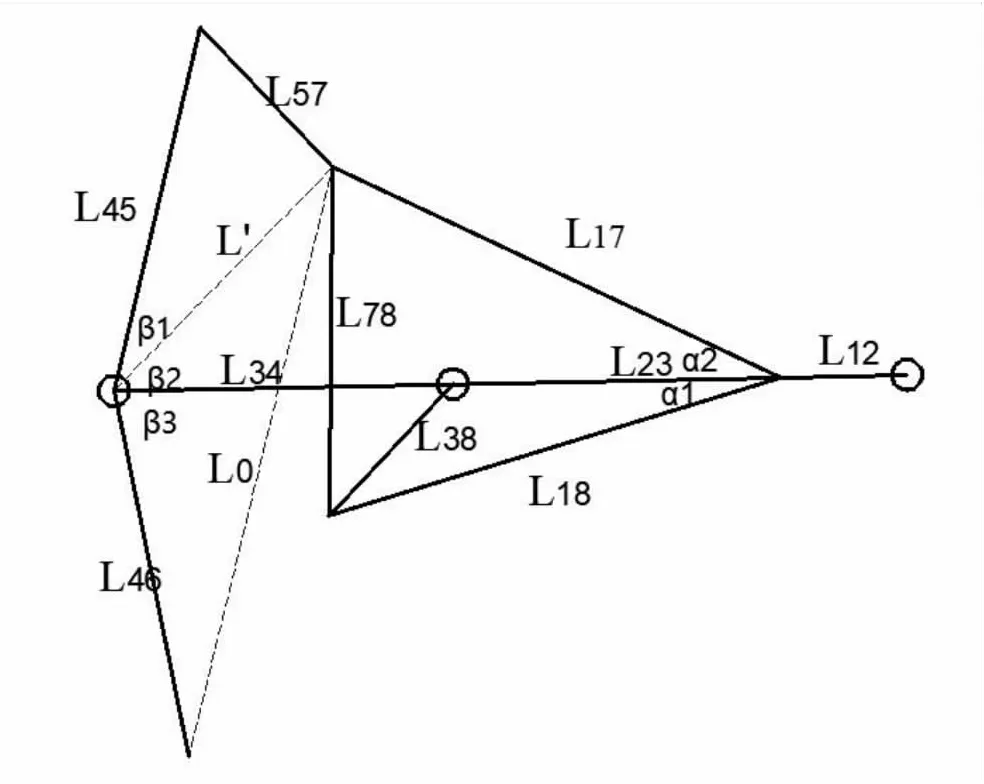
在极限位置一:经过计算设计出的已知参数有:
α1+α2=41°
L'=201 mm
β1=31°
β2+β3=124°
以及各杆件长度,如表1所示。
根据图3(a)中几何关系可以得出运动公式。行走件此时刻距离L0最短:
(2)
代入数据计算可得:
L0=401.5 mm
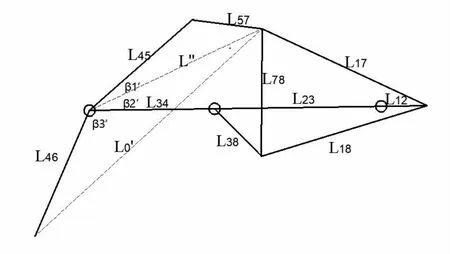
在极限位置二:经过计算设计出的已知参数有:
L''=344 mm
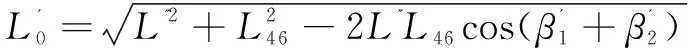
(3)
代入数据计算可得:
(a)极限位置一
(b)极限位置二
图4为助行器步距示意图,结合图3中的几何关系,利用三角函数计算可得:

图4 助行器步距示意图
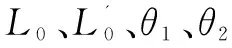
运动时上下浮动高度为:
确定了两极限距离为318 mm后,由于运动过程中一侧腿部件运动,另一侧支撑在地面上,故实际步长为636 mm。在运动过程中上下浮动的高度仅为15.7 mm,可以保证平稳运行。
4 主要构件静力学仿真分析
该助行器的行走件及框架上的电机支撑板在运动过程中起着关键的作用,行走件主要支撑助行器主体以及人体的压力,电机支撑板跨度大、厚度较小,故这两处最容易出现变形甚至失效,应当对进行静力学分析和校核。在Solidworks软件中,建立构件三维模型,设置各尺寸参数,选择材料类型,划分网格,最后得到构件应力分布情况。
4.1 行走件模型静力学分析
行走件模型的应力分布如图5所示。

图5 行走件应力分布
经有限元仿真分析后可知,最大应力产生的位置位于杆件中部铰制孔内壁表面上,其应力值为22.94 KPa,由于行走件选择材料为6061铝合金,其屈服强度为55 MPa。为满足安全使用要求,取材料安全系数1.5,则所对应的许用应力为36.7 MPa,可知实际最大应力值仍远小于许用应力,故此结构满足强度要求。
4.2 电机支撑板静力学分析
电机支撑板模型受到的应力如图6所示。
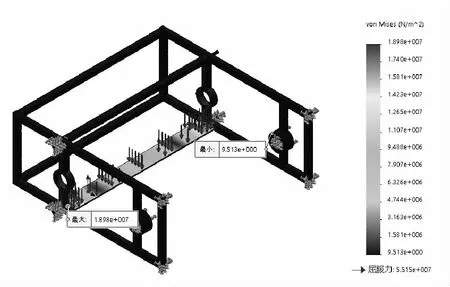
图6 电机支撑板应力分布
在电机支撑板两端与框架结合处出现最大应力值,最大应力19.0 MPa,同样,支撑板的材料也是选用6061铝合金,其许用应力36.7 MPa,最大应力小于许用应力,支撑板强度亦满足要求。
5 运动仿真分析
由于助行器的使用者是下肢有运动障碍的人士,因此在运动过程中最注重的就是运动的平稳性和安全可靠性,与之最直接相关的就是驱动电机的转速,由于助行器仅有一个电机作为驱动,故需要通过动力学仿真分析确定出最大运动速度以保证使用者的安全,再经调速握把调整至自身需要的运动速度。
将单个周期时间延长至12 s以进行仿真模拟及数据分析。各杆件质量分布均匀,几何中心与质心重合,之后根据在SOLIDWORKS中建立的腿部三维模型,在ADAMS中进行助行器腿部的运动仿真分析。
首先添加重力加速度,然后新建连杆Link1:选择连杆Link,依据表1中各杆件尺寸数据设置长Length、宽Width、厚Depth的值,接着用同样的方法,新建连杆Link2、连杆Link3、连杆Link4、连杆Link5,再添加运动副joints1:点击Connectors中的转动副,选择机构的两个连杆和一个连接点,同样建立joints2-joints8,最后,建立驱动Motions:选择Motions中的旋转,在Rotational Joint Motion 中设置速度Speed即可。由于腿部活动构件运动方式可简化为圆周运动,所以可将驱动系统函数简化为简单周期函数。
对助行器行走部件进行两个周期的仿真运动,仿真后进行后处理,在行走件质心建立Measure,对其质心的角速度与角加速度进行测量,以助行器沿水平地面运动的方向为X方向,宽度方向为Y方向,高度方向为Z方向建立空间坐标系。同时在行走件与地面接触的腿部建立Measure,对X方向与Z方向上的位移进行测量,最后得到在单个周期内助行器行走件质心的角速度与角加速度图像和行走件与地面接触的腿部的X方向和Z方向上的12个时刻测量数据,如表2所示。

表2 单个周期内行走件着地点与初始位置的距离
根据结构设计和运动仿真分析结果,进行了实物模型制作,如图7所示。为了验证上述仿真分析结果的合理性,进行实物实测验证。

图7 实物模型
实验过程中,为了能更加方便地得出仿真与实物的数据关系,将一个完整的周期等分为十二个时刻,测量各时刻的位置状态,与表2中仿真结果进行对比,如图8所示。图中两条折线分别表示表2中所列X向和Z向位移,图中偏差为各个实测值与表2中仿真数据偏差值(为表示清楚,图中偏差值放大5倍显示)。
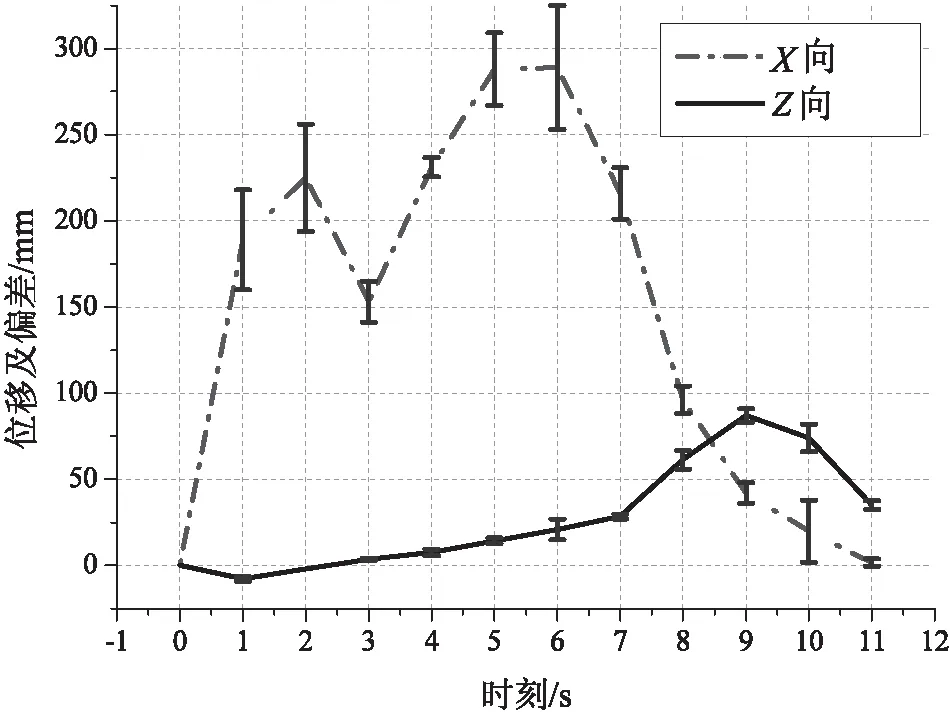
图8 仿真分析与实物测量结果之差
可以看出,在第7个时刻(即第6 s),行走件距离初始位置最远,此时的实物测量数据与仿真结果偏差最大,为7.2 mm,相对偏差3.9%。在第10个时刻(即第9 s),行走件抬起的高度最大,约为87 mm,故本助行器具备跨越80 mm高度障碍的能力。此时,在Z方向得出的实物测量结果与仿真结果相对偏差最大,为5.7%。实测结果表明,运动仿真分析结果误差不大,具有较高仿真精度。
图9所示为用ADAMS仿真软件得到的单周期内行走件速度、加速度及位移变化曲线。
图9(a)为质心点的角速度与角加速度图像,横坐标为时间,纵坐标为角速度。从图中可以看出:腿部行走件质心角速度在约7.5 s时达到最大值为22.60 deg/s,而腿部行走件质心角加速度在约8.1 s时达到最大值,为22.45 deg/s2。此结果表明,当一侧行走件处于最高位置时,另一侧行走件与地面接触,此刻运动速度较快,可以以较短的时间通过障碍物。
图9(b)为行走件分别在X方向与Z方向上的相对测定点位置的距离。根据仿真测试所得数据可以看出:行走部件与地面接触的腿部沿X方向上运动单个周期的位移约为0.3 m,而沿Z方向上运动单个周期的位移略小于0.1 m,此结果与上述腿部杆件运动分析结果一致。由于确定老年人最大行走速度范围为1.06 m/s~1.28 m/s,根据仿真结果得到的步距进行电机参数的选用,确定选用转速为6 000 rpm的电机,经减速比为1∶25的减速机减速输出后,最大运动速度为1.2 m/s,同时设计采用调速转把实现老年人对日常生活步行步速不同的需求,所以此行走部件设计满足设计要求。
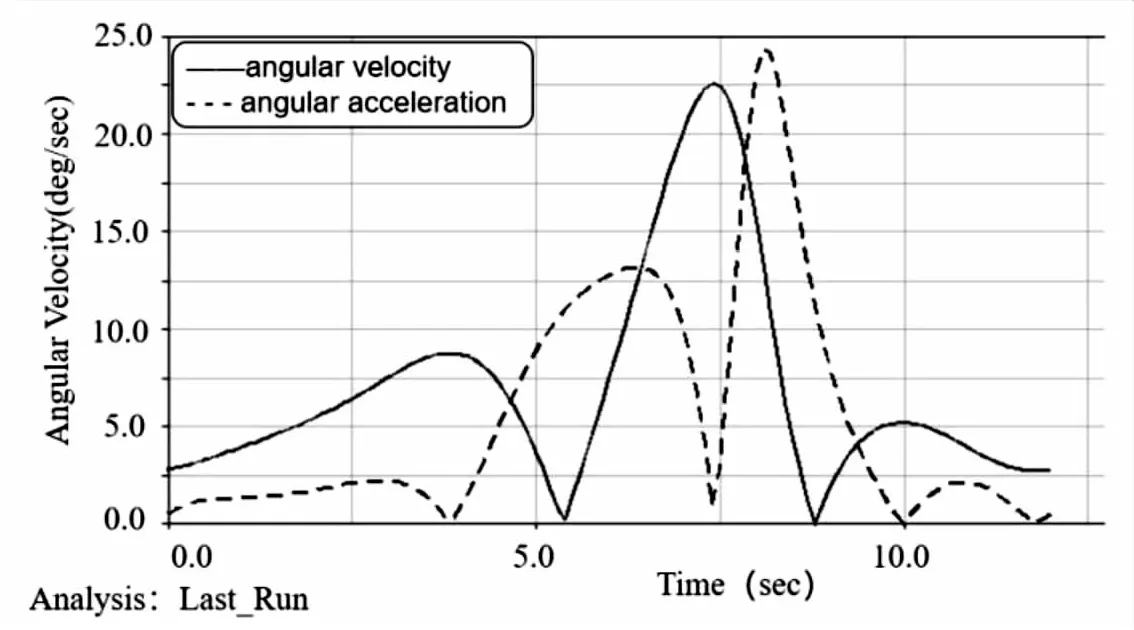
(a)单周期内行走件质心角速度与角加速度曲线
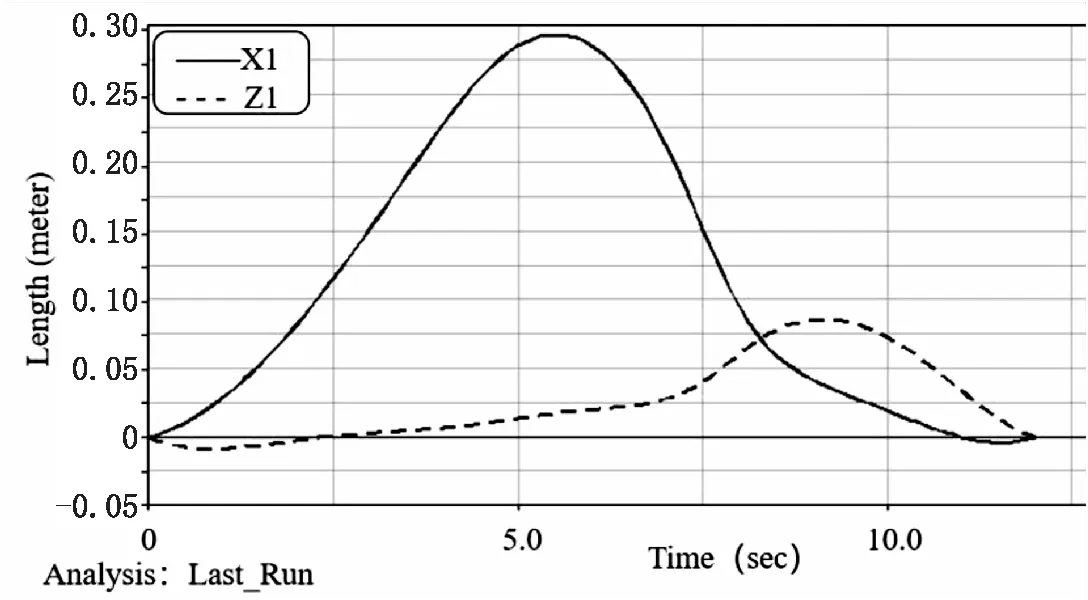
(b)单周期内行走件位移曲线
该助行器可以为老年人或腿部有障碍的残疾人提供支撑和前进的动力,速度可以由使用者自行控制,安全可靠,可以为使用者提供恢复行走能力的信心,为老龄化严重的局势做出贡献,促进社会和谐。
6 结束语
设计了一种腿轮结合的行走式助行器,该助行器结构简单,利用齿轮和同步齿形带的精确传动比省去多电机驱动的繁琐,驱动方便,解决了常见老式助行器依靠人力费时费力的问题。
首先,对助行器总体结构进行了设计,并对其传动机构的自由度进行了计算分析;随后,确定了机构各主要构件尺寸,选定材料;进一步,针对机构中最重要的腿部杆件进行运动分析,得到了机构运动的两个极限位置;接着利用SOLIDWORKS软件建立了机构模型,对机构的重要构件进行了静力学分析与强度校核;最后,使用ADAMS软件进行机构运动仿真,进行实物制作,并将实测结果与运动仿真结果进行对比,验证了所设计机构的运动性能。运动仿真与实物测量结果对比表明,机构运动时的速度、加速度、步距等参数值与理论计算值相比误差很小,验证了助行器行走步态的稳定性,证明了所设计的助行器可以辅助下肢行走,达到助行和康复训练的目的。

