深度卷积神经网络中激活函数的研究
李一波,郭培宜,张森悦
(沈阳航空航天大学 自动化学院,辽宁 沈阳 110000)
0 引 言
AlexNet网络模型在图像识别分类、目标检测、语音文字识别等方面都表现得十分突出[1]。AlexNet虽然不是首个被创建的卷积神经网络模型(convolutional neural networks,CNN),可是它是首个引起众多研究者所关注的卷积神经网络,具有里程碑意义。AlexNet模型是由多伦多大学教授Geoffery Hinton同他的学生Krizhevsky等人共同设计,2012年创下Imageclassification比赛的新记录,并获得了ImageNet Large Scale Visual Recognition Challenge(ILSVRC)挑战赛的冠军[2]。同年,Krizhevesky等[3]在大型图像数据库ImageNet[4]的图像分类竞赛中提出的AlexNet模型,以超越第二名11%的精确度获得了冠军,使得卷积神经网络成为学术界关注的焦点之一。随着机器学习研究领域的不断拓展,AlexNet也被许多学者作为首选的网络模型,通过改进和优化,其分类精度不断提高。
深度卷积神经网络的观点起初来源于人工神经网络,而网络中激活函数则是人工神经网络模型训练过程和学习非线性函数过程中不能或缺的一部分。如果网络模型不使用激活函数,神经网络每一层的输出都将等价于前一层输入的线性函数,那么无论神经网络将会有多少层,输出都将是输入的线性组合,这种情况使网络模型成为最基本的感知器,深度神经网络将变得失去本身意义[5]。因此,使用激活函数作为神经元来引进非线性因素是十分必要的,可以使得神经网络能够任意逼近任何非线性函数,进而使神经网络能够应用到更多的非线性模型中。Krizhevsky等人在AlexNet中提出了ReLU激活函数来训练网络[6],其优点是前向区间为线性函数,加快了模型训练的收敛速度,解决了softsign、Softsign、Tanh等常见激活函数中的梯度消失问题,然而ReLU激活函数很可能导致一些神经元在模型训练中无法激活。为了解决这种神经元“死亡”现象,改进了ReLU激活函数,使其在x小于零的负轴区间由Swish函数来替代,使负半轴的ReLU激活函数称为非线性激活函数,有效地解决了x小于零的部分神经元不能激活的问题,并且在x大于零的区间部分范围内由ReLU激活函数来替代,提高收敛速度的同时也能够提升参数的利用率,并且降低了过拟合现象的发生率,很好地提高了AlexNet的鲁棒性。
针对AlexNet网络中激活函数ReLU在网络训练中产生的神经元死亡和均值偏移问题,结合反正切函数和对数函数的优势,在传统激活函数ReLU基础上提出了一种新的激活函数sArcReLU。将文中构建的激活函数训练网络模型并应用于公开数据集分类实验中以验证其建立的网络的性能。实验结果表明,利用sArcReLU激活函数训练的深度卷积神经网络在分类精度和适应性方面均有明显的改善。
1 AlexNet模型结构
AlexNet总共有650 000个神经元,63 000万个神经连接,60 000 000个网络参数。AlexNet网络结构简单,引入了许多新方法来达到稳定的收敛速度[7],网络结构如图1所示。网络模型结构共8层,其中分别含有五层卷积层和三层全连接层,包括了LRN局部响应归一化层和Dropout正则化。此网络模型在图像分类领域有着较为出色的优势[8]。

图1 AlexNet结构模型
图像数据输入格式是227×227×3,其中227表示输入图像的宽度和高度,3表示输入图像的三原色R、G、B通道模式,所以不需要对输入的数据集进行额外的格式裁剪。第一、二层计算均为卷积,ReLU,最大池化层和归一化,第二层的输出结果与256个特征图进行了卷积操作。网络中的第三、四层只需要进行卷积和ReLU操作。第五层的过程和第一层的过程类似,区别只在于没有经过归一化处理。网络最后将其第五层的输出转变为长向量,输入到三层全连接结构的卷积神经网络模型中,再运用Softmax回归函数即可计算其分类准确值。
2 模型的改进
AlexNet网络采用ReLU非饱和线性函数,激活值的获取相对简单,只用一个阈值,省去了原本复杂的运算过程,相较于常见的非线性S型激活函数Tanh、Sigmoid等收敛速度更快[9],改善了梯度消失和收敛不稳定的缺点。图2为ReLU与其他常见激活函数的曲线对比。
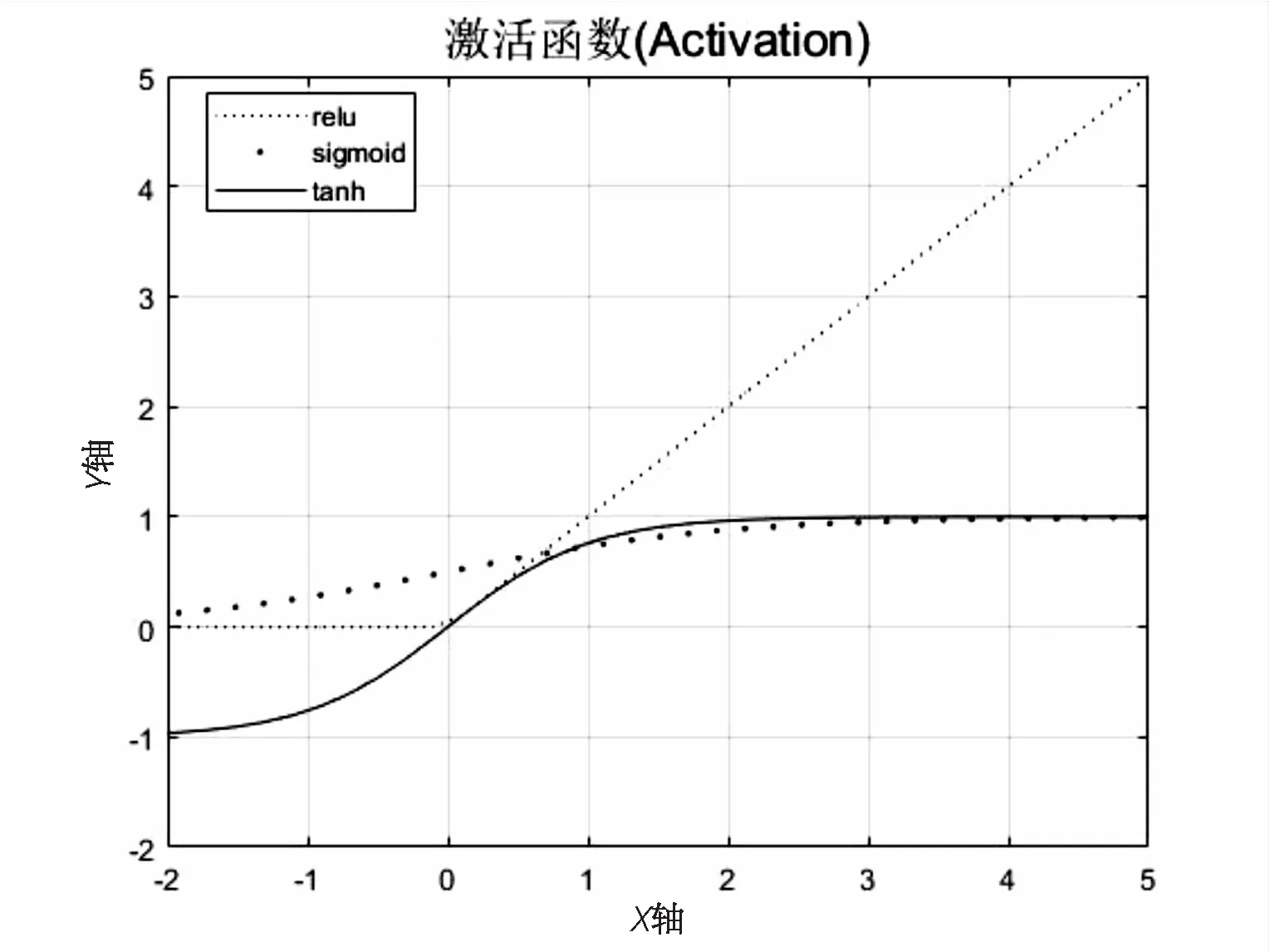
图2 ReLU与常见的激活函数曲线对比
Tanh函数换言之是Sigmoid函数的一种变换类型,Tanh函数的输出值在[-1,1]区间内,而Sigmoid函数的输出值则在[0,1]区间[10]。Tanh和Sigmoid都拥有饱和区,ReLu函数在x大于零时导数一直是1且不变,十分有助于解决梯度消失、梯度爆炸等问题,促使加快训练速度。
一般地,当网络模型后向传递过程时,且使用梯度下降法求解网络参数,Sigmoid激活函数向下传导的梯度中包含了有关自身输入的导数f'(x),当输入值进入饱和区时,f'(x)的输出值逐渐接近于零。此特性十分容易导致梯度消失现象,所以深度神经网络一直很难得到有效的训练,也是阻碍神经网络发展的重要原因之一[11]。
其中ReLu激活函数的数学表达式为:
f(x)=max(0,x)
(1)
经过图2分析,ReLu激活函数曲线也存在很多不足,例如当输出值恒大于或等于零时,易导致均值偏移的缺点,均值偏移会导致神经元将前一层网络的非零均值输出的信号作为输入信号,使参数的计算复杂度大幅度增加。处于网络模型训练过程的前向传播过程时,“强制”稀疏性作用会使网络中的某些神经元一直不会被激活,与其相对应的参数也一直不会被更新,所以会致使一些好的特征被屏蔽。众所周知,神经“死亡”和强制稀疏性的缺点对网络模型的收敛速度和网络性能影响很大[12]。

(2)
ArcReLU函数导数如下:
(3)
由图3分析,ArcReLU激活函数导数值恒为正值。根据导数特征,可说明函数明显呈单调递增特性。当激活函数拥有单调特性时,单层网络能保证其为凸函数,由此推断出该函数在训练过程中更易收敛。

图3 ArcReLU及其导数的图像
由于ReLU归类于分段线性非饱和的函数,其与传统的S型激活函数作对比发现,ReLU函数随机梯度下降收敛速度更快,而且函数计算过程更加简洁明了。相较于Sigmoid激活函数,ReLU稀疏特性更加明显。然而稀疏性也将会带来更高的错误识别率并且降低了网络模型的有效容量。通过分析激活函数,不仅计算过程更加简洁,而且负半轴的输出会得以更好的保存。在负轴使用了反正切函数进行替换,不仅可以使均值更趋向于零,缓解了函数均值易偏移的缺点,并且其负半轴部分具有软饱和性,使其不会轻易出现神经元“死亡”的现象,同时具备单调递增的特性,进一步提高了收敛速度。
文中结合ArcReLU激活函数设计了一种新的激活函数,记为sArcReLU,表达式如公式(4)所示,函数图像如图3所示。
(4)
上述公式中,系数s表示超参数,取值范围为[0,1)。当输入为负值时,函数的梯度与参数s不相关;当输入为正值时,函数值取决于超参数。
改进后激活函数的图像如图4所示。由函数图像分析可以得到初步结论,该函数在其定义范围内可导并且单调递增,现只需证明该函数在其原点处的可导特性。以下证明过程中将x大于零的部分称为f1,x小于等于零的部分称为f2,过程证明如下:
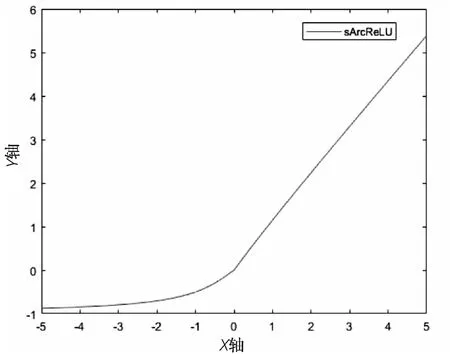
图4 sArcReLU函数图像
f(0)=f(0-)=f(0+)=0
(5)
(6)
(7)
式(5)说明sArcReLU在原点连续且具有定义。由式(6)与式(7)的结果分析,函数都存在且相同,依据导数的定义,该函数在零点处可导。
sArcReLU的偏导数为:
从上述公式可看出,sArcReLU激活函数的导数值始终大于零。根据导数定义,证明函数具有单调递增特性。当激活函数始终具有单调特性时,单层网络可以保证其为凸函数[14]。当激活函数中x大于等于0,即神经元处于兴奋激活状态时,梯度随着x的增加而不断下降,并且最终收敛于1。当x小于零,即神经元处于抑制区域时,具有接近于零的梯度s。
sArcReLU函数具有以下优势:
①负轴的输出值保持非零值,因此激活函数拥有保留梯度变化的特性,即可以有效解决由ReLU强制置零特性导致的神经元“死亡”缺点。
②超参数s使得激活函数输出值可变,消除了当ReLU取正值时的线性特性,使得网络更新过程更接近于生物神经元接收刺激信号时展现的生物特性,并且应用于不同的数据集将会得到不同的最优值,也使改进后的激活函数更具备适应性。
③由于超参数s的存在,正半轴的值保持可变性,可以实时修正数据的分布稀疏性,保留了网络快速收敛的特性。
3 实验与分析
UC Merced Land Use(UCM)数据集为公开的遥感数据集。数据集中的遥感图像由工作人员从美国地质调查局“市区图像”集合中的大图像中手动提取[15]。其中包括美国不同城市地区的21种地物的遥感图像,数据集中每一类有一百幅,共2 100幅,空间分别率为1英尺,分别具有R、G、B三个颜色通道。21类场景分别为农田、机场、棒球场、沙滩、建筑、丛林、密集住宅区、森林、高速公路、高尔夫球场、港口、十字路口、普通住宅区、房车停车场、立交桥、停车场、河流、跑道、高级住宅区、储油罐、网球场。其中部分场景之间有部分重叠,比如住宅区分了密集住宅区、普通住宅区、高级住宅区三类。21类场景图像的部分样例如图5所示。

图5 UCM数据集样例图
实验采用开源框架Tensorflow-1.10.0,编程软件python3.6.6实现模型结构构建,采用的CPU是Intel(R)Core(TM)i5-8500 CPU @3.00 GHz,8G内存,64位windows10操作系统。
按照9∶1的比例将UCM数据集中每一个场景的高分辨率图像随机分为90张训练数据、10张测试数据。初始学习率选取0.000 1、0.001、0.01、0.1、1,实验结果如图6所示。

图6 不同初始学习率对应的loss值
随着学习率不断扩大,网络的损失值逐渐减小,随后loss值又开始小幅度增大。由图6分析选取0.1作为初始学习率最为合适。
为了验证激活函数参数s取值对分类结果的影响,s分别取值0,0.01,0.1,0.4,0.7,1进行测试,实验结果如表1所示。
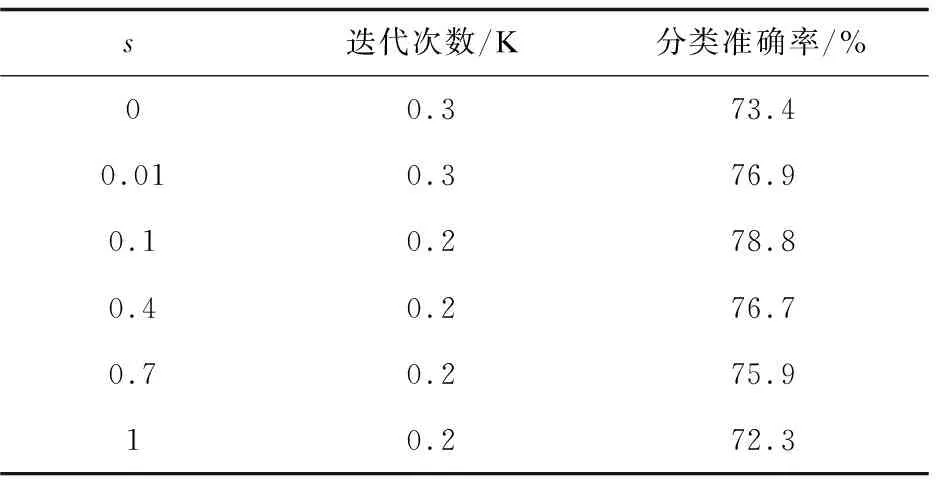
表1 超参数s分析
实验结果表明,当s=0时,激活函数退化为ReLU,准确率就是AlexNet经典网络模型训练得出的结果,即73.4%。当s=0.1时,网络会在1 000次时最先达到收敛状态,而且分类效果最好,网络准确率将会达到78.8%。
在数据集UCM和同等条件下对三种激活函数ReLU、ArcReLU、sArcReLU做了训练测试。实验结果如表2所示。

表2 数据集UCM下的准确率
通过结果分析,用sArcReLU激活函数训练的AlexNet在分类准确率上比受其他两个激活函数的AlexNet更胜一筹。
为了验证提出的激活函数的适应性,新建了一个数据集UCM-NWPU,选取NWPU-RESISC45和UCMerced_LandUse中相同15种场景,每种场景有900张,总有13 500张,对图像尺寸归一化,调整输入图像的尺寸统一为256×256×3。训练集是在每类图像场景中随机挑选出其中90%图像,因此原有训练集共有12 150张图像,剩下的1 350张图像就将作为测试集。
若选取的学习率过大,十分有可能会直接越过最优值;若选取的学习率过小,优化的效率可能过低,长时间就无法收敛。同上一个实验一致,经过测试,本实验的学习率为0.1时测试结果最好,激活函数中超参数s选取0.1时效果最好。实验结果如下所示:
图7和图8分别是sArcReLU作为激活函数在数据集UCM-NWPU上训练验证的分类准确率和损失函数曲线。
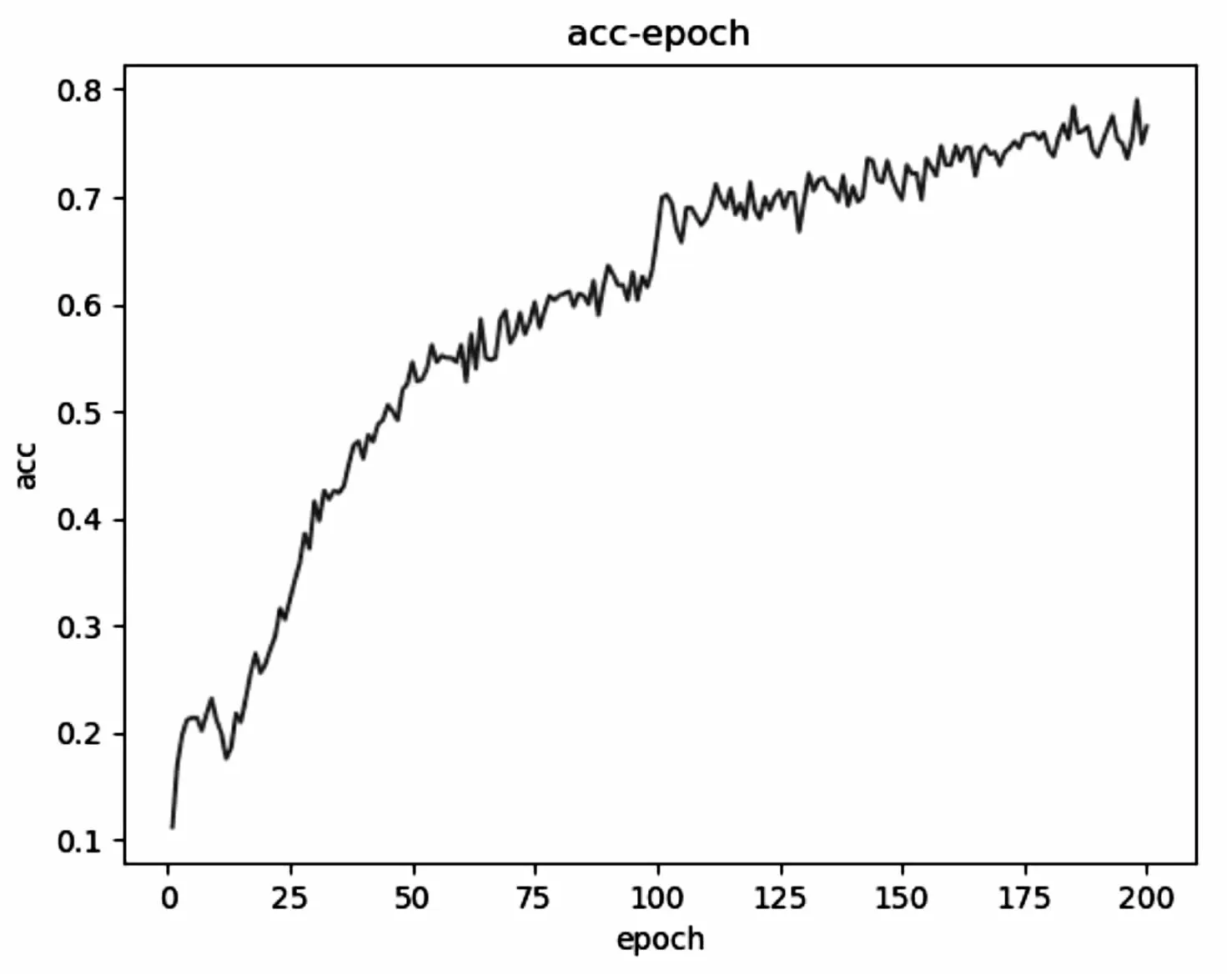
图7 准确率
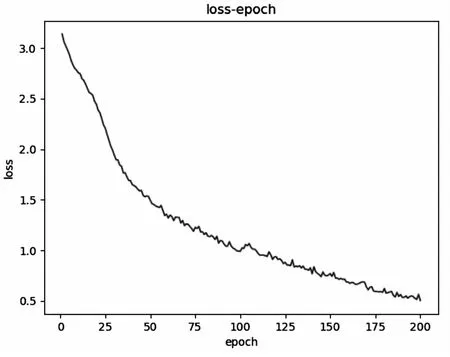
图8 损失函数曲线
4 结束语
文中设计了一种新激活函数sArcReLU,并且与ReLU和ArcReLU激活函数进行了实验分析和比较。实验证明:sArcReLU激活函数能够明显提高网络迭代速度并且有效降低训练的误差率。表明sArcReLU中超参数s对迭代次数和准确率有一定的影响。下一步研究工作的重点将放在激活函数中超参数s的优化上,以进一步提高激活函数sArcReLU的性能。

