基于时间序列模型的农产品价格指数预测研究

摘要：本文为了能够更好的预测农产品价格指数（简称API）以及更好地制定农业政策，对从2003年起至2020年第二季度的季度数据来进行时间序列分析。通过分析数据特点，消除其不平稳性，然后来建立适合拟合和预测该数据的ARIMA模型和SARIMA季度乘积模型。通过对建立的三种模型的比较，挑选出最适合的模型，然后利用该模型对API进行预测。

关键词：API;ARIMA模型;SARIMA模型;预测

一、引言

农产品价格频繁异常波动，不仅会引起社会整体物价水平的波动，还影响到人民生活水平的稳定，而且还将给广大农产品生产者和经营者带来额外的市场风险，与此同时也给国家的宏观经济运行带来不稳定因素。因此，稳定农产品价格已经成为我国宏观经济调控的重要目标。通过运用合理的方法对农产品价格的短期变动做出较准确的预测，以把握农产品价格总体水平的未来走势，可以为农产品生产者和经营者规避农产品价格波动风险、为政府平抑农产品价格波动提供预警和决策依据。农产品生产者价格指数是反映一定时期内，农产品生产者出售农产品价格水平变动趋势及幅度的相对数。该指数可以客观反映全国农产品生产价格水平和结构变动情况，满足农业与国民经济核算需要[1]。

二、数据介绍及处理

（一）数据来源

本文所使用的数据为2003 年第一季度～2020 年第二季度的我国农产品生产价格季度同比指数（上年同季=100），共73个数据（数据来源于国家统计局），将农产品价格指数的月度时间序列命名为API，由于该时间序列是以上年同季为基期计算得到的，本身已剔除了一部分季节因素，为了进一步减缓该序列的波动程度，使该序列平稳化以满足建模的条件，下文将对序列API 进行预处理并用该序列建模分析。

（二）数据处理

1.数据类型分析

在对数据进行建模分析之前，我们要对时间序列数据API的平稳性和纯随机性进行检验，根据检验结果来判断时间序列的类型。对于平稳性检验的方法比较常用的是时序图，自相关系数、偏自相关系数[2]。

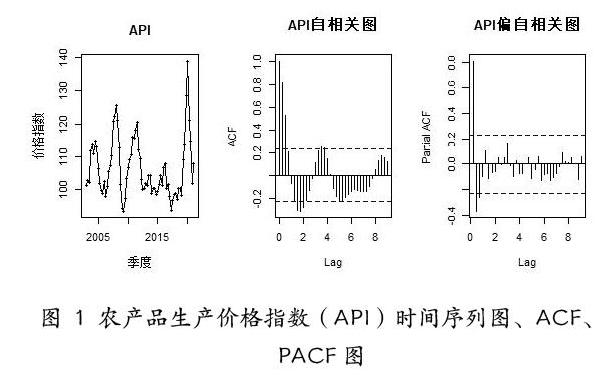
可以从图1 看出序列并没有明显的趋势，但是其存在比较大的波动，并且在最后有明显的上升，初步判断该序列是非平稳的。图1 中的自相关图显示这个指数序列没有一个样本自相关系数严格等于零，并且自相关系数递减到零的速度相当缓慢，在很长的延迟时期内，自相关系数以一定的周期趋势在0 附近随机波动。这是具有季节趋势的非平稳序列的一种典型的自相关图形式。自相关函数图显示延迟3 阶的自相关系数在2 倍标准差范围之外，还具有明显衰减的阻尼正弦波动特征，说明有周期变化规律。

偏自相关图表示除了1-3 阶偏自相关系數在2 倍标准差范围之外，其他阶数的偏自相关系数都在2 倍标准差范围内，这是一个偏自相关系数3 阶截尾的典型特征[3]。

2.消除不平稳性

根据上文的分析可知，API 数据是不平稳的非白噪声序列，所以在对数据进行建模之前，要先消除数据的不平稳性。一般的方法是进行差分处理，为了确定差分阶数，需要通运用ADF单位根检验确定d。单位根检验（ADF）。单位根检验是指检验序列中是否存在单位根，如果存在单位根就是非平稳时间序列。若P 值<0.05，为平稳[4]。

对API 序列进行ADF 检验，把ADF 检验值与临界值（置信水平分别为1%、5%、10%时）进行比较，发现未通过检验，后续对其进行一阶差分、二阶差分的ADF 检验。

从表1 可以看出，1 阶差分后，t 统计量的值为-2.5802，均小于置信水平为1%、5%、10%时的临界值，实验结果表明，该序列为1 阶非平稳，即差分次数d 的值为1。

对原始序列进行一阶差分，并检验差分序列的平稳性，根据其时序图、自相关图、偏自相关图，最终判断1 阶差分后的序列是符合白噪声序列，表明该序列平稳。后续研究均在一次差分处理后的时间序列基础上展开。

三、模型建立与比较

（一）ARIMA 模型识别与定阶

根据一次差分后序列的平稳性检验结果，观察其自相关函数图和偏自相关函数图发现，这是一个截尾序列。另外，由于在前述的讨论中，已经确定了ARIMA 模型的差分项为1，因此可将模型设定为ARIMA（p，1，q）。并且从图1可以看出，该序列的自相关函数1 阶是显著的，2 阶之后数值都位于虚线内，且较1阶时下降明显，即1阶后截尾，所以先设定ARIMA（ p， d， q） ）模型中的q 值为0。同样通过偏自相关函数图，1 阶时的数据偏相关系数均较为显著，2 阶之后截尾，数据都位于虚线内。所以，先设定模型中p 值为0、1。因此，经过排列组合后，得到了4 种可能的ARIMA模型。在此，本研究选用loglikelihood 、AIC 这2 个指标对4 个可能的模型的回归结果进行比较，指标的数值越小，表示模型的拟合优度越高。

其中ARIMA（0，1，0） 的loglikelihood224.32，AIC448.64;ARIMA（0，1，1）的loglikelihood222.23，AIC446.46;ARIMA（1，1，0）的loglikelihood221.96，AIC445.92;ARIMA（1，1，1）的loglikelihood221.96，AIC447.9

从上面的结果可以看出，在上述4 个可能的模型中，综合log likelihood 、AIC指标比较，ARIMA（1，1，0）模型表现出了最好的预测性能，因此，选定的最终的模型为ARIMA（1，1，0），其模型表达式为： 1 0.2521 ） t t （B Ye 。

（二）自动定阶模型

除了上面的模型识别方法，我们还可以使用R 语言中的auto.arima 函数进行自动模型定阶，auto.arima 函数是Hyndman-Khandakar 算法[5]的一个变种，它结合了单位根检验，最小化AIC 和MLE 等评价标准来获得一个ARIMA模型。

（三）SARIMA 模型识别与定阶

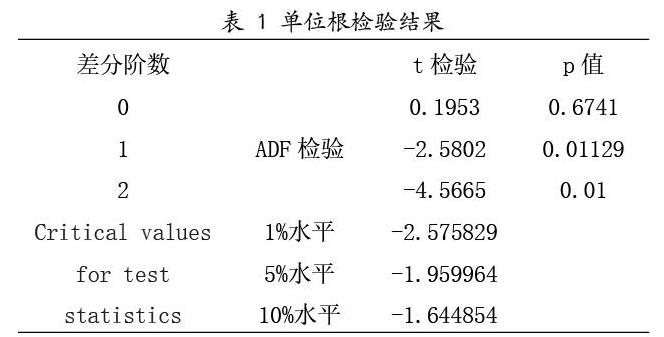
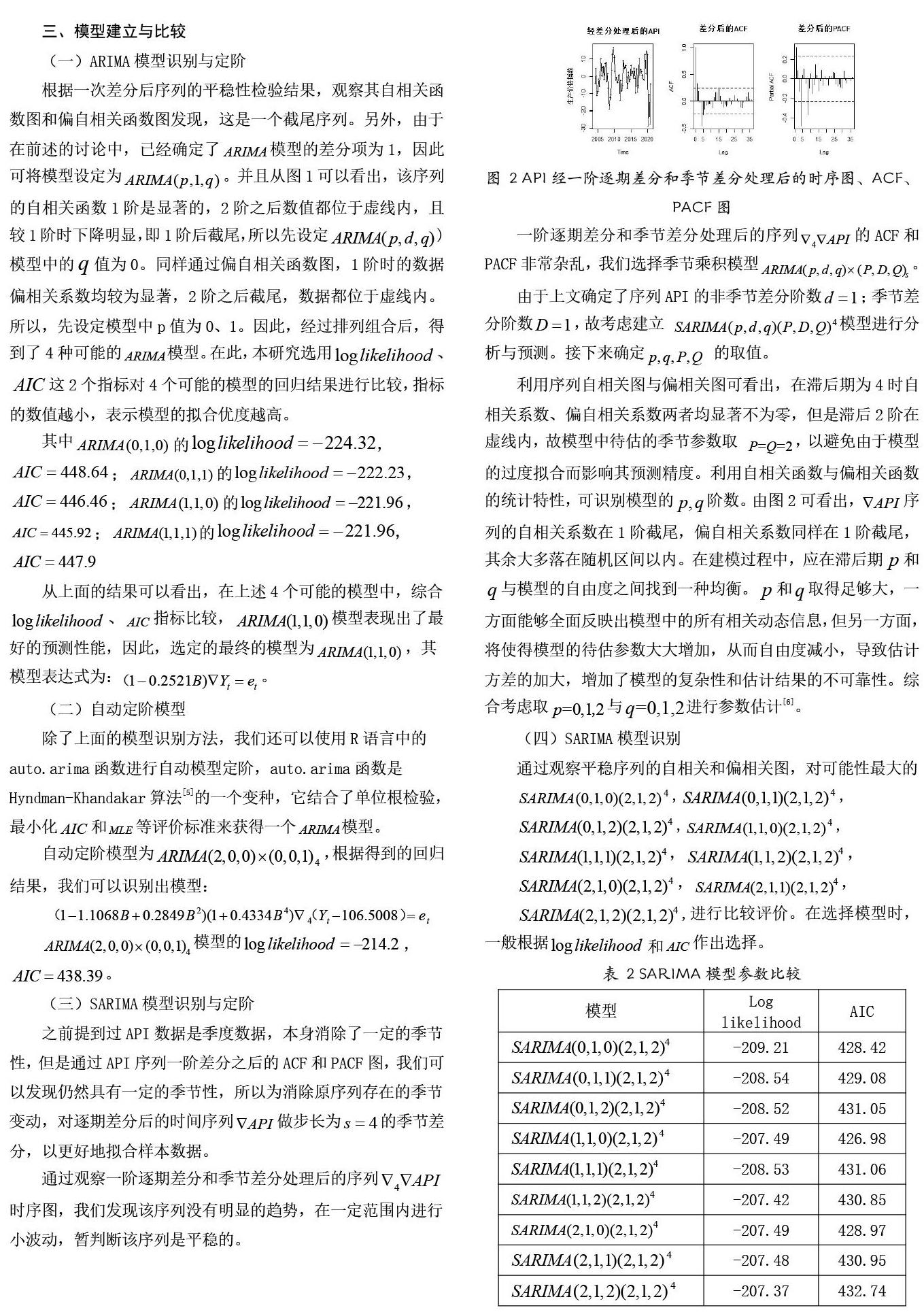
之前提到过API 数据是季度数据，本身消除了一定的季节性，但是通过API 序列一阶差分之后的ACF 和PACF 图，我们可以发现仍然具有一定的季节性，所以为消除原序列存在的季节变动，对逐期差分后的时间序列API 做步长为s4的季节差分，以更好地拟合样本数据。

通过观察一阶逐期差分和季节差分处理后的序列 API 4时序图，我们发现该序列没有明显的趋势，在一定范围内进行小波动，暂判断该序列是平稳的。

综合loglikelihood 和AIC 以及系数显著与否来看，SARIMA（1，1，0）（2，1， 2）4 是相对更优的模型。我们接下来对SARIMA（1，1，0）（2，1， 2）4进行参数估计，根据得到的回归结果，我们可以识别出模型：

（五）模型比较

上文我们已经通过三种方法识别定阶出了三种模型，接下来我们要对这三种模型进行比较选择，首先比较这三种模型的log likelihood 和AIC 值。

通过比较这两个指标，我们发现SARIMA（1，1，0）（2，1， 2）4是比较好的模型，为了进一步的比较，我们观察用三个模型对API进行12 步预测，并画出预测图，来比较三种模型预测图。

通过观察预测图，我们发现ARIMA（1，1，0）模型因为没有考虑季节因素，预测值过于平均，没有使用价值;自动识别阶数4 ARIMA（2，0，0） （0，0，1） 模型预测值的发展趋势与原序列非常接近，也体现了季节性，它的预测值比较有参考价值;我们通过季节差分后的定阶识别的SARIMA（1，1，0）（2，1，2）4季节乘积模型的预测也比较符合API 发展趋势，并且相比模型4 ARIMA（2，0，0） （0，0，1） 来说，少了一些极端值的影响，而且SARIMA（1，1，0）（1，1，1）4模型我们对经过季节差分后的平稳序列进行定阶，拟合的更加好。综上，我们最终选择SARIMA（1，1，0）（2，1，2）4模型来进行预测。

四、SARIMA 模型检验

我们通过对残差序列的时序图和ACF、PACF 图进行观察，检验残差序列是否平稳。

通过观察残差序列的时序图，残差没有明显的趋势，观察ACF、PACF 图，值几乎全部在虚线内，我们判断该模型的残差序列是平稳的。再对残差序列进行LB 检验，SARIMA（1，1，0）（2，1，2）4模型的残差序列LB检验统计量滞后4阶、8 阶、12 阶都>0.05，所以该序列是随机的。综上，我们最终判断该模型的残差序列是白噪声序列，因此该模型通过了检验[7]。

五、模型预测及结论

我们用SARIMA（1，1，0）（2，1， 2） 4模型首先计算出未来6期的预测值及其预测区间。

为了能够更加清晰的看出我们使用的SARIMA（1，1，0）（2，1， 2） 4模型预测的情况，我们画出预测图来进行观察，如图3 可以看出SARIMA（1，1，0）（2，1， 2）4季节乘积模型的预测比较符合API 发展趋势。

雖然SARIMA（1，1，0）（2，1， 2） 4模型简单，而且拟合和预测效果理想，但该模型只是对单变量时间序列进行建模及预测，我们无法从模型结构中了解到有哪些因素以及这些因素是如何影响农产品价格;而且从长期来看，其影响因素错综复杂且千变万化，加剧了农产品价格波动，因此，SARIMA（1，1，0）（2，1， 2） 4模型的短期预测结果可能更理想。

参考文献：

[1] 陈灿煌. 我国农产品价格指数短期预测——基于时间序列分解的分析[J]. 价格理论与实践， 2011（07）：55-56.

[2] Box G E P ， Jenkins G M . Time series analysis ：forecasting and control[J]. Journal of Time， 2010， 31（3）.

[3] 石韵. 基于ARIMA 时间序列模型的中国塑料制品产量预测研究[J]. 塑料科技， 2020（3）：115-118.

[4] 施龙青， 王雅茹， 邱梅，等. 时间序列模型在工作面涌水量预测中的应用. .

[5] Hyndman R J ， Khandakar Y . Automatic TimeSeries Forecasting： The forecast Package for R[J].Journal of Statistical Software， 2008， 027.

[6] 陈娟， 余灼萍. 我国居民消费价格指数的短期预测[J]. 统计与决策， 2005， 000（02X）：40-41.

[7] 方燕， 马艳. 我国大豆价格波动及其未来走势预测[J]. 价格理论与实践， 2014， 000（006）：67-69.

作者简介：

郭玉昆（1996-），女，首都经济贸易大学，汉族，山东省聊城市，硕士研究生在读，应用统计。