齿轮齿条动态啮合及传动分析的SPH数值算法研究

唐宇峰，胡光忠，曹修全，阳明君

(1.四川轻化工大学 机械工程学院，四川 宜宾 644000;2.重大危险源测控四川省重点实验室，成都 610031)

用传统的解析法进行齿轮齿条啮合及传动力学研究时，由于大量的简化难以正确反映实时的动态力学行为。而近年来发展起来的以网格为主的数值方法(如有限元法、有限差分法等)则可以对啮合接触区域的力学状态及冲击过程进行计算，如：Hwang等[1]采用有限元发法通过齿圆柱齿轮和斜齿圆柱齿轮两个例子对一对齿轮在旋转过程中的接触应力进行了分析，并指出考虑一对配合齿轮的接触应力的齿轮设计比美国AGMA标准更加准确；贾海涛等[2]采用有限元法分析了圆柱斜齿轮齿面接触动应力；闫晓青等[3]采用有限元法讨论了齿条内夹杂物、齿面蚀坑等缺陷对齿轮齿条运行的影响。然而，固定的网格在实时追踪轮齿传动，特别是当面临大变形及裂纹扩展时容易产生网格畸变而造成计算误差甚至计算中止，因此限制了其应用。

光滑粒子流体动力学(smoothed particle hydrodynamics，SPH)方法是近年来逐渐发展起来的一种纯拉格朗日无网格计算方法，目前已应在许多计算力学领域，如爆炸力学、流体力学和固体力学等领域得到了应用，如：强洪夫等[4]将SPH方法应用于宽速域岩石侵彻问题，得到了花岗岩靶板受碰撞侵彻的大应变、高应变率变形；陈佩佩等[5]采用SPH方法对非饱和岩土介质渗流问题进行了讨论；王维国等[6]采用SPH-FEM(smoothed particle hydrodynamics-finite element method)耦合的方法，研究了小当量集团装药在不同埋置深度时的土中爆炸效应；骆钊等[7]针对复杂固壁边界提出了改进，并将其应用于沙土滑坡大变形的模拟；Frissane等[8]采用SPH方法研究了射弹撞击对人体的损害；Becker等[9]通过模拟和试验的方法对比了SPH方法、光滑粒子伽辽金法和有限元法在进行高速冲击计算中的优劣。近年来，学者们逐步将SPH方法引入到机械工程领域，并取得了一些可喜的成果。如：热合买提江等[10]讨论了SPH分析中的齿轮建模方法；Imin等[11-12]研究了两齿轮啮合和相互耦合接触的SPH计算方法，将啮合粒子之间的作用力视为一种系统内力，分析了一对齿轮冲击啮合过程中最大动应力随时间的变化规律；Keller等[13]研究了旋转直齿圆柱齿轮在喷油冲击过程中的复杂两相流动，并预测了3个不同射流倾角的直齿圆柱齿轮上喷油冲击过程中的流动现象。然而总体来说，SPH方法在机械领域内的研究尚属于起步阶段，特别是对类似齿轮齿条等具有复杂几何形状的动态啮合及传统分析研究还鲜见报道。因此，构建基于SPH的新型齿轮齿条动态啮合及传动的数值计算方法：一方面能够为齿轮、齿条、轴承等复杂接触界面问题的动态力学分析提供科学依据及新的计算方法；另一方面也能够推动SPH方法在该领域内的进一步发展。

采用SPH进行齿轮齿条啮合及传动分析时，其基本思想是将齿轮及齿条模型离散为有限个无网格连接的离散点，而齿轮及齿条的物理力学参数及动态属性，如密度、质量、体积、位置、速度、加速度等都有离散点携带，并通过光滑核函数及质量守恒、动量守恒和状态方程建立离散点间的联系。相对于传统的基于网格的方法，SPH方法由于离散点间无网格连接，所以不会产生单元扭曲、网格畸变以及网格划分奇异性带来的计算误差，特别适合求解高速传递的动态力学行为。本文在传统SPH方法的基础上，针对齿轮齿条啮合及传动过程的特点，通过对啮合方式、受力特点等改进，建立了适用于齿轮齿条啮合及传动分析的SPH方法。最后用某简化的齿轮齿条动态传动过程为例，对齿轮齿条动态啮合及传动过程进行了分析。结果表明，该SPH方法可以较为准确地计算齿轮齿条啮合及传动的全过程，揭示齿轮齿条机构发生齿面点蚀及齿根破坏的力学原理，能够为该领域的计算提供一种新的计算方法，另外也推动了SPH在复杂啮合及传动机械领域内的进一步发展。

1 齿轮齿条啮合及传动分析的SPH计算基础

1.1 SPH理论基础

在SPH中，其方程构造主要有两个关键步骤组成。其一就是将任意宏观变量函f(x)数通过积分进行表示，而函数f(x)的积分表示可通过对支持域内相邻粒子的值进行累加求和近似，可用方程[14]表示为

(1)

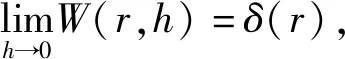
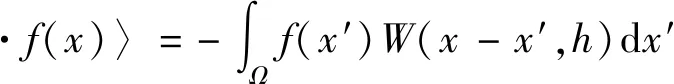
(2)

而粒子近似就是将相关的连续积分表达式转化为支持域内所有与粒子叠加求和的离散化方程，即

(3)

式中：j为粒子编号；mj，ρj分别为粒子的质量及密度；N为其支持域内临近粒子的总数。即任一函数值可用其支持域内所有粒子相对应的函数值进行加权平均而近似表达。同样的，函数f(x)的空间导数∇·f(x)的粒子近似可表达为

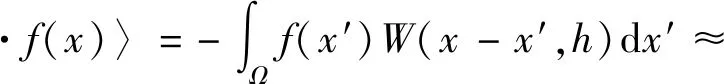
(4)

式(1)～式(4)中，光滑函数Wij的选择对离散近似起到了重要的作用，本文中选取的是一种新型的四次光滑核函数[15]，可表达为

W(R,h)=αd×

(5)

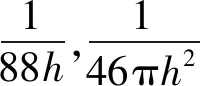
其光滑函数及其一阶、二阶导数，如图1所示。

图1 新的分段四次核函数及其一阶、二阶导数Fig.1 The NQS kernel and its one and two-order derivative

1.2 基于理想弹性模型的齿轮齿条啮合及传动分析方程的SPH离散

利用1.1节所述SPH的基本理论，SPH形式下的连续性方程和动量方程可以表示为

(6)

(7)

式中：v为速度；α和β为坐标方向；σαβ为总应力张量；Fα为外力引起的加速度，如重力、齿轮齿条相互作用力及固壁边界作用力等；Πij为Monaghan[16]提出的人工黏度，可以防止粒子相互接近时产生的非物理穿透，其表达式为

(8)

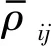
(9)

(10)

同时，引入了XSPH的速度平均方法公式

式中，ε为修正因子，本文中选0.3。

根据线弹性动力学理论，SPH形式的本构方程可以表示为

(11)

式中：G为剪切模量；K为体积模量；εi,γγ为主应变之和；δαβ为狄克拉函数；ωαβ为Jaumann应力率，其表达式为

(12)

2 齿轮齿条啮合及传动作用力的SPH实现

在齿轮齿条冲击及传动过程中同时存在连续性及非连续性，即齿轮、齿条构件内部为连续体，而齿轮齿条构件之间接触具有离散性。虽然当齿轮齿条粒子处于啮合状态时，其啮合部分可采用连续体方法、核估算进行计算，然而由于齿轮齿条间不断处于啮合及脱离啮合状态，当其作用关系从啮合向脱离啮合状态转变时，采用核估算方法会在齿轮齿条间会产生与实际情况不符的拉伸力，与实际啮合状态不符。在本文中，对齿轮齿条啮合及传动过程进行了以下考虑：

(1)如上所述，齿轮和齿条在各自构件内部为连续体，因此其构件内部的作用力可以通过核估算进行计算。而在齿轮及齿条发生相互啮合作用时，也可通过核估算方法来提高接触力的作用的计算精度。然而，为正确表达齿轮齿条粒子啮合状态，避免齿轮齿条的提前作用，交界处粒子在计算啮合冲击力时，其影响域之和应等于齿轮齿条啮合粒子的平均间距，即

(13)

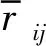
(2)当齿轮齿条粒子从啮合状态向非啮合状态转化时，虽然此时齿轮齿条粒子仍处于啮合状态，但如果仍按本章方法进行处理，会在齿轮齿条粒子间产生与实际情况不符的拉应力。因此，本文在此状态下将连续方程中的粒子间相互啮合作用力定义为0，并且在齿轮齿条粒子处于啮合状态时，给予齿轮及齿条粒子一个具有弹簧特性的相互作用的外力，该力与齿轮齿条粒子的变形及弹性模量有关，即距离越近说明变形越大，则外力随着变形及弹性模量的增大而越大，而距离越远说明变形越小，则外力随着变形及弹性模量的减小而越小。在二维条件下，此外力可表达为

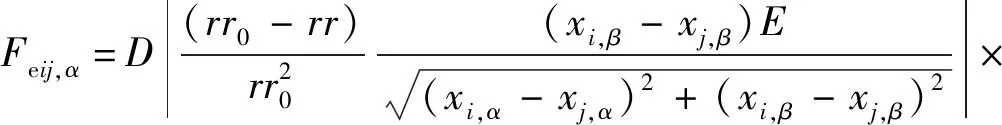
(14)

式中：Feij,α为齿条粒子j对相啮合的齿轮粒子i的外力；rr0为齿轮齿条啮合粒子初始的平均间距；rr为齿轮齿条啮合粒子某时刻的实际间距；sign为符号函数，即括号内若为正则返回1，为负则返回-1；D为常数，取相对速度平方相等的量级；E为弹性模量。

基于本章理论，编制了适用于齿轮、齿条等高速啮合及传动分析的SPH计算程序，其计算流程如图2所示。

图2 采用SPH方法进行齿轮齿条啮合及传动分析的计算流程Fig.2 Calculation flow of gear rack meshing and transmission analysis using SPH method

3 数值算例

本文以一对简化的齿轮齿条算例为例进行分析。算例中齿轮模数为4 mm，压力角为20°，齿宽为20 mm，齿轮沿顺时针旋转，转速为15 rad/s，为避免齿轮齿条过度冲击，给予齿条沿X负方向，大小为0.353 m/s的初速度。齿轮齿条的材料均为球磨铸铁，弹性模量为173 GPa，泊松比为0.3，密度为7 800 kg/m3。为节约计算成本，对齿轮齿条结构进行了一定的简化，粒子初始间距为0.001 m，齿轮齿条共离散1 053个粒子，其中齿轮粒子为395个，齿条粒子为658个，另外固壁边界虚粒子322个，时间步长为4×10-8s，计算1×106个时间步，共计0.04 s，粒子初始装配状态如图3所示。粒子在0.008 s，0.024 s，0.04 s时刻的运动状态如图4～图6所示。

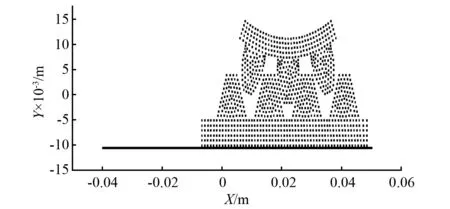
图3 齿轮齿条粒子初始状态Fig.3 The initial state of particles of gear and rack

图4 齿轮齿条在不同计算时刻时的运动状态Fig.4 The motion state of gear and rack at different calculation times

为观察齿轮齿条运动状态，在齿轮齿条上随机各选取了一个粒子观察其速度随时间的变化情况，图5(a)为齿轮齿条粒子在X方向的速度变化曲线(vx)，图5(b)为齿轮齿条粒子总速度变化曲线。由图5可知，由于本算例中齿轮齿条初始速度不同，在运动初期产生了速度波动，而随着计算时刻的增加，齿轮齿条速度趋近恒定，并与实际传动速度相符。

由图5可知，在约0.072 s时由于齿轮齿条间相互啮合作用发生速度值的较大变化，选取该点查看其Mises应力分布，如图6所示。可知此时齿轮和齿条在此时产生啮合额，且在啮合点处应力最大。随后，应力向四周进行传播，并在齿根处产生应力集中，其应力大小和发生时刻略小于啮合点处应力。分析结果表明，齿面点蚀及齿根破坏是齿轮齿条机构破坏的主要形式。

图5 齿轮齿条粒子在传动过程中的速度变化规律Fig.5 The law of the velocity change of the gear and rack particles during transmission

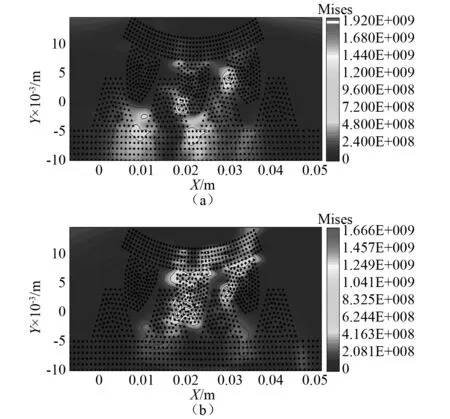
图6 齿轮齿条啮合过程Mises应力分布及传递Fig .6 Stress distribution and transmission of mises during gear bar meshing process

为了验证结果的合理性，采用有限元方法进行了对比，图7为有限元计算的内力结果及传递过程，可见其应力大小、应力传递过程与SPH方法的结果基本一致，证明了本文算法可以较好地模拟齿轮齿条啮合及传递过程。

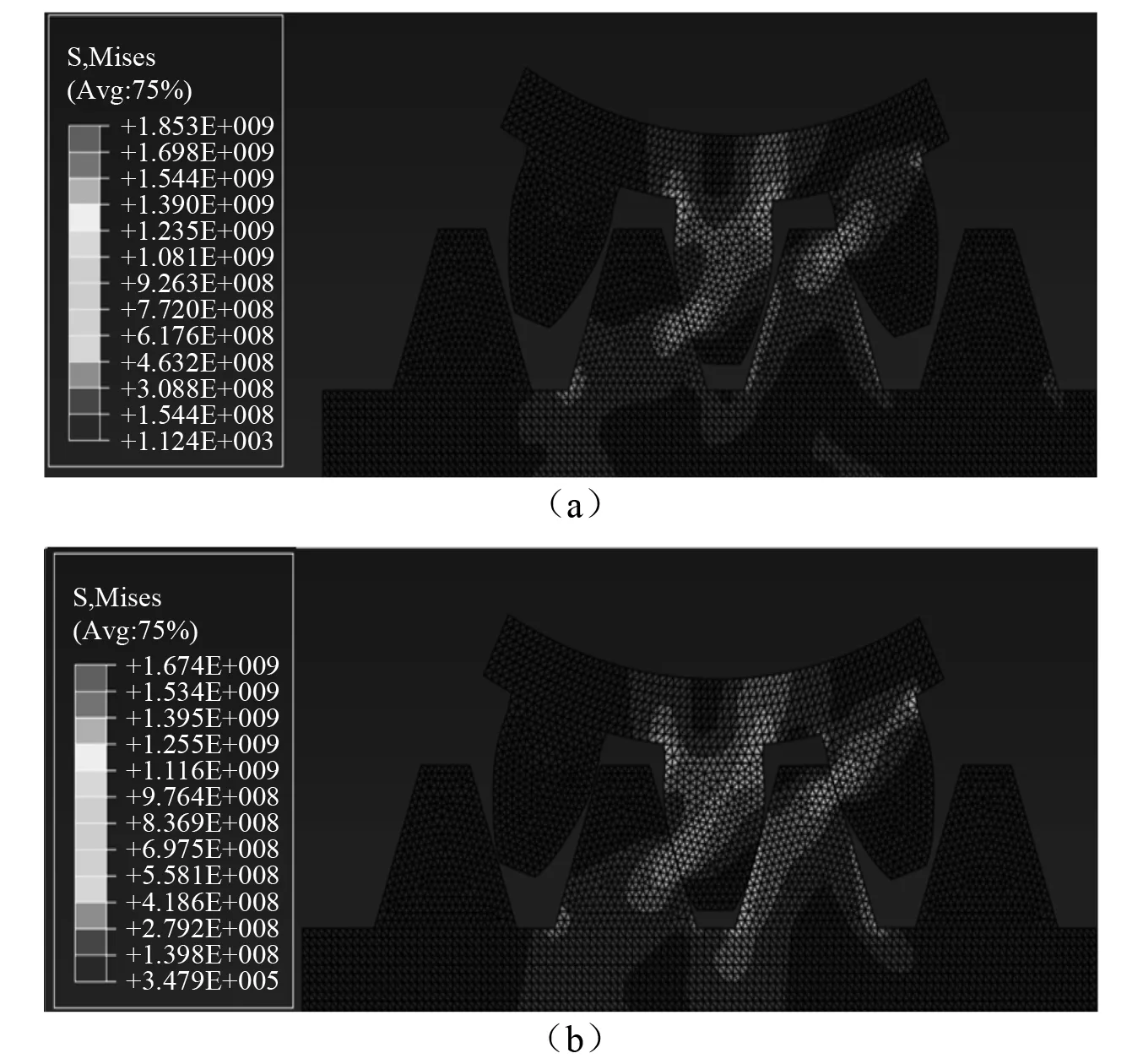
图7 有限元方法的Mises应力分布及传递Fig.7 The Mises stress distribution of the gear and rack using finite element method

如本章分析结果可知，通过本文提出的SPH方法，可以动态获取齿轮齿条啮合在任意时刻的运动状态、应力分布、速度分布、运动过程中最大应力等参数，揭示结构破坏的原因，可为齿轮的优化设计、强度校核、判定损伤影响等提供可靠依据。然而应该指出的是，为了减少计算成本，在本算例中对齿轮进行了简化，若要对完整的齿轮齿条进行分析，则应建立更加完善的齿轮齿条模型，同时研究更为高效的并行算法提高计算效率。

4 结 论

(1)本文提出了一种基于SPH的齿轮齿条动态啮合及传动分析的SPH算法，该算法可以解决以往SPH算法仅能分析准静态啮合问题的不足，能够有效地模拟齿轮齿条动态啮合及传动数值分析问题，推动了SPH在该领域内的进一步发展。

(2)对一个齿轮齿条动态啮合及传动的数值算例进行了分析，分析结果有效揭示了齿轮齿条机构发生齿面点蚀及齿根破坏的力学原理，并与有限元方法分析结果对比验证了本文提出的SPH算法的正确性。该法可广泛应用于齿轮、齿条、轴承等复杂动态接触机构的问题分析，为该领域的数值分析提供了一种新的思路。

(3)由于本文基于串行SPH程序进行计算，完整的齿轮齿条模型会导致计算成本过高而难以进行。因此，发展高效的并行算法是未来需要进一步做的工作，从而进一步推动SPH在该领域内的进一步发展。