N形装甲板抗穿甲弹侵彻性能数值模拟

杨 姝，于 晨，康玉彪，裴连政，亓 昌，景乙桐

(1.大连理工大学 汽车工程学院 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.汽车安全与节能国家重点实验室，北京 100084；3.大连理工大学 宁波研究院，浙江 宁波 315016)

装甲防护技术是武器高速发展和全球战略局势不断改变下逐步发展起来的一项核心技术。功能强大、种类多样的反装甲武器的出现提高了对军用车辆和特殊用途民用车辆的装甲防护要求，高性能防护装甲成为国内外研究的热点。其中，抗弹性能是装甲防护研究的焦点之一。

由于硬度高、韧性好、价格低、易加工等优点，高强钢一直是抗弹侵彻研究的重点对象。Jena等[1]研究了热处理对高强钢力学性能和弹道防护性能的影响，认为可以添加合金元素或调整工艺来提高高强钢的弹道防护能力。Børvik等[2]进行了5种不同性能高强钢的弹道试验和数值模拟，结果表明，强度和韧性是影响高强钢抗弹性能的主要因素。张自强[3]进行了穿甲弹侵彻不同倾角均质高强钢板的弹道试验，结果发现，钢板放置角度的不同导致其抗弹效果不同。黄雪峰等[4]通过数值模拟研究发现，随着钢板放置角度增大，穿甲弹内部结构件应力增大，容易发生变形和失效。Rosenberg等[5]通过穿甲弹和长杆弹侵彻斜板的试验和仿真发现，斜置装甲钢板凭借材料本身的高强度和对弹丸的不对称作用力，可有效地使弹丸减速、偏转和破碎。Paris等[6]对14.5 mm穿甲弹侵彻不同倾角和厚度装甲钢板的过程进行了研究，发现钢芯的破碎程度随钢板厚度和倾斜角度的增加而增加。多层防护装甲主要利用装甲板的空间距离使弹丸充分破碎，增大破片散布面积。结合斜板和多层防护结构的特性，Wen等[7]研究了一种将3层平行铝板结构的中间层倾斜的N型防护结构，通过与具有相同面密度的3层平行铝板结构的超高速侵彻试验和仿真结果对比，初步证实倾斜的中间层具有提升结构防护性能的作用。

本文针对军车弹道防护需求，研究一种由孔板、斜板和基板组成的N形结构高强钢防弹装甲板的抗弹性能。利用非线性显式动力学有限元软件LS-DYNA进行了7.62 mm穿甲弹侵彻N形装甲板的数值模拟，揭示了穿甲弹侵彻N形板过程中的弹靶破坏现象和钢芯耗能规律，进而分析了弹着点位置对N形板抗弹性能的影响。在此基础上，提出了一种锥形孔板，并以子弹贯穿孔板后的偏转角度和剩余速度为评价指标，对比了其与圆形、方形孔板的抗弹性能，发现锥形孔板具有一定优势。最后，通过多组数值模拟得到了锥形孔N形装甲板的弹道极限，并与等质量均质钢板的弹道极限进行了对比。

1 模型及验证

1.1 结构模型

N形装甲板由孔板、斜板和基板三部分组成。其中，孔板利用孔的边缘效应使子弹偏航并导致弹体破坏。Ali等[17]研究发现，当孔径与子弹钢芯直径接近时，弹体受到破坏的程度最大。因此，本研究中孔的半径R取3 mm；两孔中心横向和纵向间距L1，L2均取8 mm。斜板在连接孔板和基板的同时，可进一步偏航、破坏弹体并使弹速下降。基板则利用材料自身强度抵御弹体冲击。N形装甲板及其结构参数，如图1所示。

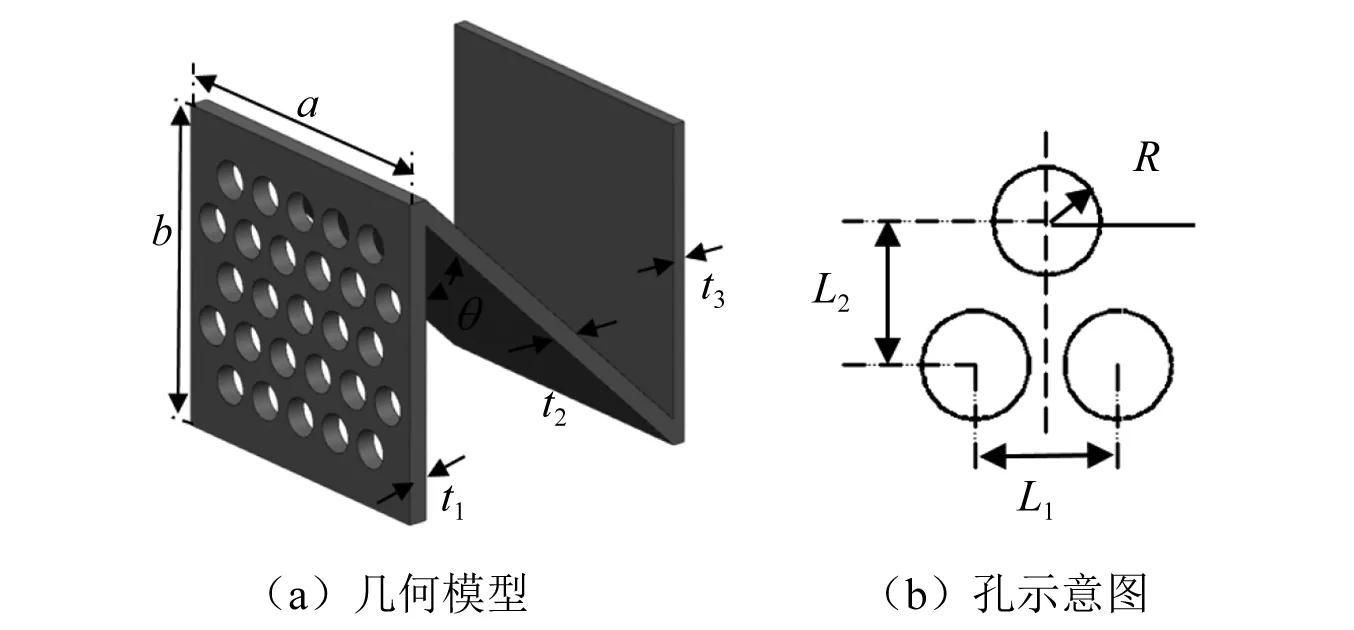
图1 N形装甲板及其结构参数Fig.1 Diagram and structural parameters of N-shaped armor plate

王建波等研究发现,靶板的抗弹性能受非冲击区域影响较小，考虑模拟计算时间，在数值模型中N形板尺寸a×b取50 mm×50 mm，总厚度取9 mm，即t1+t2+t3=9 mm，主要尺寸参数取值，如表1所示。

表1 N形装甲板主要尺寸参数Tab.1 Main dimension parameter values of N-shaped armor plate

侵彻能力很强的小口径穿甲弹是目前战场上应用较多且对军用车辆最具威胁的侵入体之一。因此，选择典型的54式7.62 mm穿甲弹作为侵彻体，其弹体长度为37.8 mm，外径为7.8 mm，钢芯长度为28.2 mm，直径为6.2 mm。穿甲弹的结构及尺寸参数，如图2所示。其内部组成从左到右依次为底座、钢芯和填充剂；外部为被覆层。

图2 7.62 mm穿甲弹结构示意图及其尺寸(mm)Fig.2 Schematic diagram of 7.62 mm armor-piercing projectile and its dimensions (mm)

1.2 有限元模型

图3 侵彻靶板后的钢芯前段部分Fig.3 The front portion of core after penetrating target plate

据此，为提高计算效率，建模中对穿甲弹进行一定简化：忽略弹体内部的填充材料，同时将钢芯前段设为刚性材料。为保证计算精度：对弹体前段网格做加密处理，网格尺寸设定为0.1 mm；对弹体中后段，网格尺寸沿轴向逐渐增大；末端网格尺寸为0.2 mm。靶板网格尺寸为0.35 mm。穿甲弹有限元模型剖视图，如图4所示。

图4 穿甲弹有限元模型Fig.4 Finite element model of armor-piercing projectile

1.3 材料模型及参数

N形高强钢装甲板、穿甲弹钢芯及被覆层均采用J-C(Johnson-Cook)材料本构和损伤模型参数定义；三者均采用M-G(Mie-Gruneisen)状态方程描述。它们能较准确地模拟材料在高速冲击和侵彻过程中的高应变率变形，以及涉及温度、密度、应力和应变等的非线性行为。J-C材料模型中的等效应力表示为应变率函数、应变函数与温度函数的乘积，可写为

(1)

J-C损伤破坏模型可表示为

(2)

式中：εf为等效断裂应变；D1～D5为失效参数；σ*为应力三轴度，σ*=σH/σ，σH为平均应力。

J-C材料模型中损伤参数D是一个累积量，可表示为

(3)

式中：Δε为一个积分循环中的等效塑形应变增量；εf为当前时间步下的等效断裂应变。当累积损伤参数D值达到1时，材料发生失效，相应的单元将从模型中删除。主要材料模型参数值，如表2所示。

表2 被覆层、钢芯中后段和靶板材料参数值[19-20]Tab.2 Material parameter values of coating,steel core middle and rear,and target plate[19-20]

M-G状态方程表达式为

(4)

式中：m为压缩比，m=r/r0-1，r为当前材料密度，r0为初始材料密度；C为声速；S1，S2和S3为M-G状态方程拟合参数；g0为Gruneisen参数；α为一阶体积校正系数；E0为材料的比内能。M-G状态方程参数值，如表3所示。

表3 Mie-Gruneisen状态方程参数值Tab.3 Parameter values of Mie-Gruneisen state equation

钢芯前段和底座分别采用刚体材料(MAT_ RIGID)和分段线性塑性材料(MAT_PIECEWISE_ LINEAR_PLASTICITY)模型描述，其主要参数值如表4所示。

表4 钢芯前段和底座材料参数值Tab.4 Parameter values of steel core front end and base materials

1.4 数值模拟方法验证

图5 穿甲弹侵彻高强钢板有限元模型Fig.5 Finite element model of armor-piercing projectile penetrating high-strength steel plate

试验与仿真得到的子弹侵彻两种靶板的最终结果，分别如图6和图7所示，数据对比如表5所示。

图6 7.62 mm穿甲弹侵彻9 mm高强钢板Fig.6 Results of 7.62 mm armor-piercing projectile penetrating 9 mm high-strength steel plate

图7 7.62 mm穿甲弹侵彻20 mm高强钢板(mm)Fig.7 Results of 7.62 mm armor-piercing projectile penetrating 20 mm high-strength steel plate (mm)

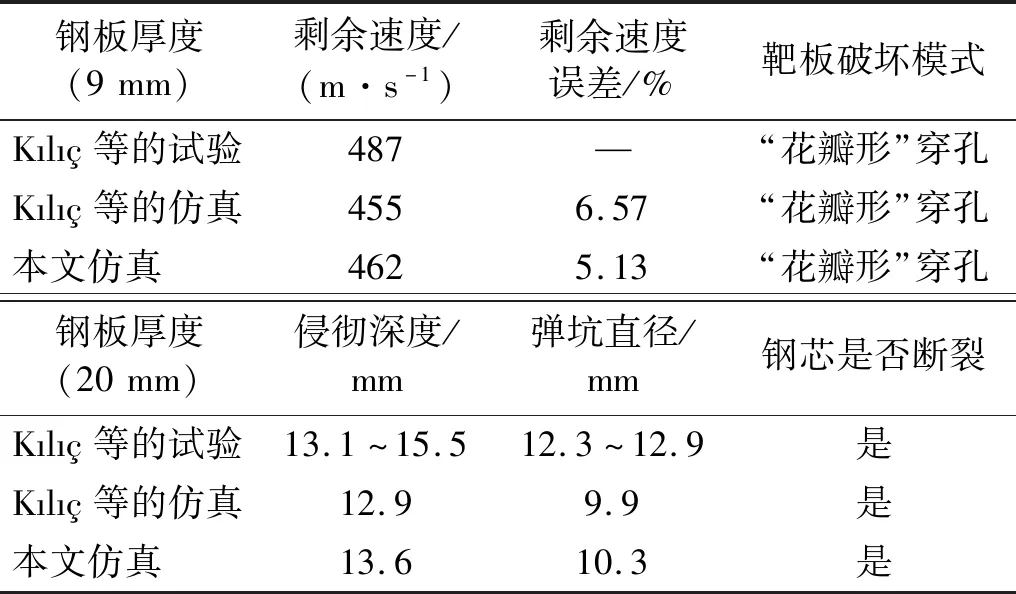
表5 试验与仿真数据对比Tab.5 Comparison of test and simulation data

由图6～图7和表5可知：在穿甲弹高速冲击下，9 mm高强度装甲钢板遭到贯穿，靶板背面形成“花瓣形”外翻；试验测得贯穿后子弹剩余速度为487 m/s，本文模拟计算结果为462 m/s，相对误差为5.13%。20 mm高强装甲钢板能有效防御穿甲弹的冲击，钢芯发生断裂且其前段嵌埋于钢板内部；靶板侵彻深度和弹坑直径的仿真结果分别为13.6 mm和10.3 mm，与试验值相差不大。上述结果验证了本文数值模拟方法的有效性和准确性。

2 数值模拟结果分析

2.1 N形装甲板抗弹侵彻过程分析

穿甲弹侵彻N形装甲板的有限元模型，如图8所示。靶板三部分的厚度比设为3∶4∶2，即孔板、斜板和基板厚度t1，t2和t3分别为3 mm，4 mm和2 mm；子弹以854 m/s垂直入射，弹着点位于孔洞边缘上侧；靶板四周采用全约束。

图8 穿甲弹侵彻N形装甲板有限元模型Fig.8 Finite element model of armor-piercing projectile penetrating N-shaped armor plate

穿甲弹侵彻N形装甲板的典型时刻数值模拟结果，如图9所示。基于子弹运动姿态和N形板损伤模式，可将侵彻过程分为3个阶段：

图9 穿甲弹侵彻N形装甲板数值模拟结果Fig.9 Simulation results of armor-piercing projectile penetrating N-shaped target plate

(1)阶段1(1～40 μs)。子弹高速垂直侵彻孔板，在弹着点处形成高压区，导致孔板材料发生破坏并向外飞溅。此外，高压冲击波向四周传播并导致临近孔洞区域变形破坏，如图10所示。另一方面，在孔的边缘效应作用下，首先与N形板接触的穿甲弹被覆层破碎分离；弹体和靶板间产生不对称的相互作用力，弹体受弯矩载荷产生弯曲和偏转，偏转角度约为6.3°。由于钢芯材料的高硬度、低韧性，受到的剪切应力超过了其抗剪强度，出现了折断现象，与Chocron等[21]的试验结果具有较好的一致性。

图10 子弹贯穿后N形装甲板的失效模式及有效应力分布Fig.10 Failure mode and effective stress distribution of perforated N-shaped armor plate after penetration

(2)阶段2(40 ～77 μs)。虽遭到折断破坏并产生姿态变化，子弹剩余速度仍高达807.5 m/s，依然具有较大的动能和较强的侵彻能力，并斜向侵彻斜板。弹体侵彻斜板使斜板材料在弹道方向上的密度急剧增加，弹道阻力增加。同时，斜板法向的材料密度却未发生变化，其对弹体的阻力远小于沿弹道方向的阻力。由于在侵彻均质靶板的过程中，弹体向阻力最小的方向运动，使得弹体向弹道方向回正。在此过程中，由于受弯矩作用，弹体发生断裂；完全穿透斜板后，弹体已不再是一个整体，而是分散成几部分碎块(见图9)。

(3)阶段3(77 ～144 μs)。钢芯碎块继续侵彻作为“最后一道防线”的基板。相比完整钢芯，碎块与基板接触的面积增加，因而贯穿后在基板上形成的损伤面积也较大。最后，部分贯穿基板的钢芯碎块以378 m/s的速度偏转射出，另一部分散落于斜板和基板的间隙。与初始速度下垂直侵彻的完整钢芯相比，偏转射出的钢芯碎块质量和动能较低，剩余动能仅占钢芯初始动能的14.9%，侵彻能力大大减弱。

综上所述，对于高速侵彻的穿甲弹，N形装甲板可同时利用孔板的边缘效应和斜板的倾角效应完成有效抵御。

2.2 弹着点位置对N形装甲板抗弹性能的影响

考虑到孔板的结构特点和子弹冲击位置的随机性，参考秦庆华等对孔结构装甲板的研究，选取5个典型位置分别进行数值模拟，研究弹着点位置对N形装甲板抗弹性能的影响，如图11所示。

1.孔中心；2.孔边缘左侧；3.三孔之间；4.孔边缘上侧；5.孔边缘下侧。图11 5个典型弹着点位置Fig.11 Five typical impact locations

不同弹着点位置下的子弹钢芯动能时间历程曲线，如图12所示。结合仿真结果可知：

图12 不同弹着点位置下的钢芯动能时间历程曲线Fig.12 Kinetic energy time history curves of steel core at different impact locations

(1)当弹着点位于孔中心时，贯穿靶板后钢芯剩余动能Ek最大，为358.03 J。该位置属于孔板材料最少的“薄弱”区域，对子弹的防御能力最弱。并且，由于孔板的边缘效应未有效发挥，子弹的运动姿态变化较小，贯穿孔板后的钢芯基本完整，并仍保持垂直姿态继续侵彻斜板和基板。

(2)当弹着点位于孔边缘左侧和三孔之间时，钢芯剩余动能Ek分别为322.39 J和325.01 J，基本相等，且钢芯均碎裂成几部分。其中，弹着点为孔边缘左侧时，贯穿后钢芯的剩余动能主要集中在中后段，此时钢芯前段刚性体部分在侵彻过程中破坏较大，耗能较多；而当弹着点位于三孔之间时，剩余动能则主要集中在钢芯前段刚性体部分，说明此部分动能损耗较少，而钢芯中后段耗能较大。

(3)当弹着点位于孔边缘上侧和孔边缘下侧时，钢芯的最终动能损耗最大，比初始动能分别下降了89.0%和86.8%。这是由于最初侵彻孔板时钢芯即受到不对称力作用而发生破碎，侵彻能力大为降低；其次，斜板的倾角效应使钢芯发生二次破坏，动能再次耗散。尤其当弹着点位于孔边缘上侧时，贯穿孔板后偏转的钢芯与斜板的接触面积最大，受的斜板阻力也最大，动能耗散很快。此时，钢芯速度快速下降，侵彻能力也随之大幅减弱。

综上所述，弹着点位置的不同会导致钢芯受到的靶板结构的作用效果不同，钢芯的侵彻路径和剩余速度也随之发生改变。

2.3 3种构型孔板抗弹性能对比

考虑到加工制造的便利性，目前作为附加装甲的孔板主要采用圆形孔和方形孔，针对这两种孔板抗弹性能的研究已较为充分[22]。事实上，孔的形状可在满足制造约束的条件下任意变化。据此，本文提出一种具有锥形孔的孔板，并对其抗弹性能进行数值模拟研究。

为简单起见，选取具有3种穿孔形式的单板进行抗弹性能数值模拟，分别为圆形孔板、方形孔板和锥形孔板，如图13所示。3种孔板尺寸相等，长×宽×厚均为50 mm×50 mm×3 mm；孔的个数及排布规则一致，即相邻两孔中心横向和纵向间距均为8 mm，共计5排，27个孔。锥形孔的锥角为30°，其大端直径与圆形孔直径和方形孔边长相等。

图13 3种构型孔板Fig.13 Perforated plate with three bore configurations

研究的弹速范围为500～850 m/s，取步长为50 m/s，对3种构型孔板分别进行8组不同入射速度下的穿甲弹侵彻过程仿真，子弹均垂直入射孔边缘上侧。

贯穿孔板后钢芯的偏转角度α随入射速度vi的变化曲线，如图14所示。由图14可知：①贯穿3种构型孔板后钢芯偏转角度的变化与入射速度变化的规律相似，即随着入射速度增加，偏转角度不断下降；这是由于入射速度的增加使得孔边缘材料对弹体的作用时间缩短，子弹发生失稳的时间相应的减少导致。②入射速度相同时，子弹贯穿方形孔板后钢芯偏转角度相对较小；这是因为当方形孔边长与圆形孔及锥形孔大端直径相等时，方形孔面积最大，相邻孔间的材料最少，导致侵彻过程中施加于弹体的作用力最小。③锥形孔板对子弹的偏转效果最好，这与其自身特点有关。在子弹侵彻过程中，锥形孔板孔洞边缘和锥面处的材料对子弹前端持续施加侧向力，从而使其发生较大偏转，如图15所示。

图14 以不同入射速度贯穿3种孔板后钢芯的偏转角度Fig.14 Deflection angle of the bullet steel core after penetrating three types of perforated plates with different initial speeds

图15 子弹侵彻锥形孔板过程中的受力示意图Fig.15 Schematic diagram of force on the bullet when penetrating perforated plate with conical bores

贯穿3种孔板后的钢芯剩余速度vr随入射速度vi的变化曲线，如图16所示。相同入射速度下，锥形孔板使钢芯速度下降最多，圆形孔板次之，方形孔板最少。模拟结果同时显示，贯穿锥形、圆形孔板后钢芯发生折断破坏，而此现象在方形孔板上未发生。

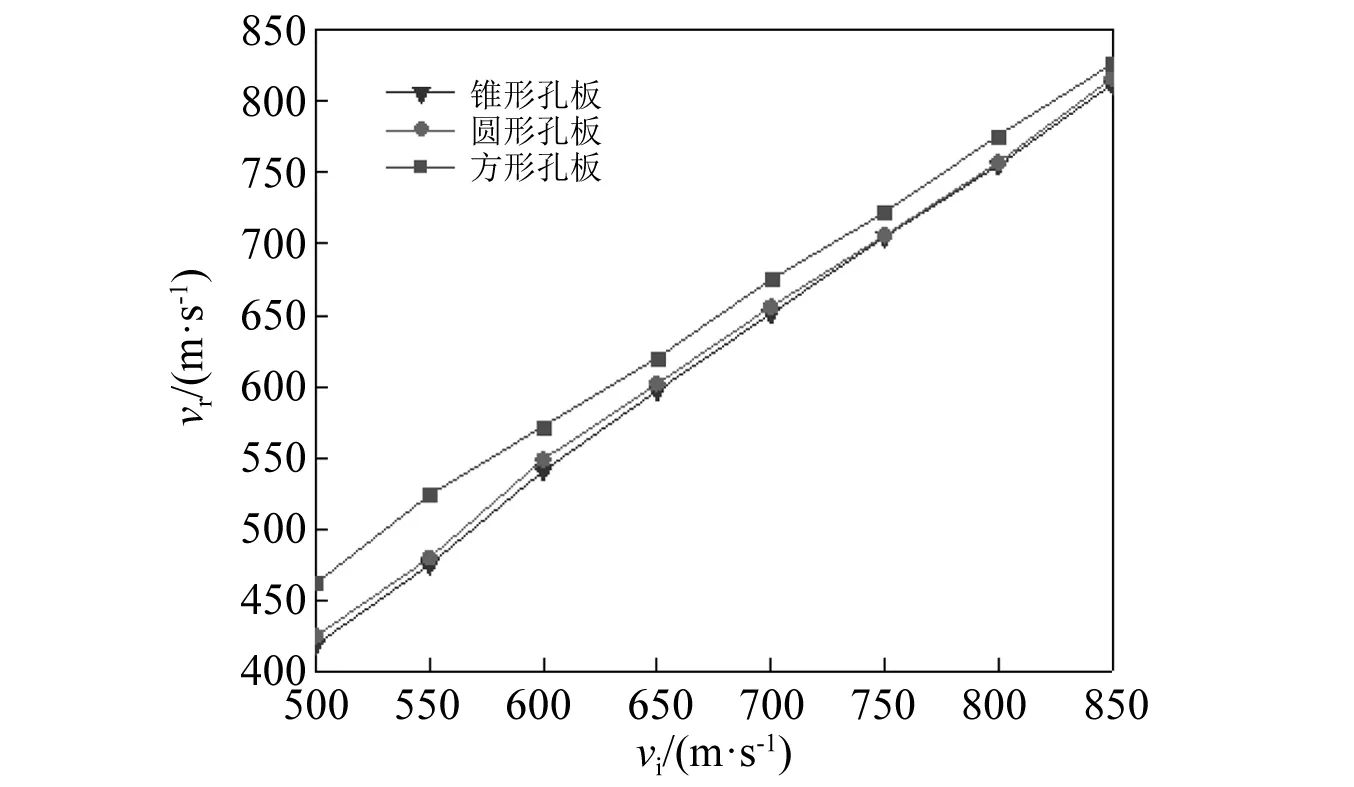
图16 以不同入射速度贯穿孔板后钢芯的剩余速度Fig.16 Residual speed of the bullet after penetrating the perforated plate at different speeds

综上所述，在改变子弹运动姿态和破坏弹体完整性方面，锥形孔板比圆形孔板和方形孔板表现更优，可进一步应用于N形装甲板。

2.4 锥形孔N形装甲板抗弹性能分析

当衡量靶板抗弹性能时，常采用弹道极限作为评价指标。弹道极限指子弹贯穿靶板的最小入射速度，其值越大，表明靶板的抗弹能力越强。其中，v50法得到的弹道极限比较简单，在研究中经常采用。v50是指当贯穿靶板概率为50%时的子弹初始入射速度。本文采用v50法确定装甲板的弹道极限。

由2.2节可知，弹着点位置对N形装甲板的抗弹性能影响较大，当弹着点为孔中心、孔边缘左侧和三孔之间时N形板抗弹效果较差。据此，基于上述3个弹着点估算锥形孔N形装甲板的弹道极限。首先分别采用完整弹丸和钢芯以854 m/s侵彻N形装甲板的上述3个弹着点，剩余速度分别相差5.35%，5.71%和9.48%，且由于被覆层材料相对较软，并且在撞击靶板时失效，为提高计算效率，仅取穿甲弹钢芯部分进行数值仿真。7.62 mm穿甲弹钢芯侵彻总厚度为9 mm的锥形孔N形装甲板的数值模拟结果，如表6所示。由表6可知：当弹着点位于上述3个位置时，弹道极限均在765～770 m/s，取其平均值为锥形孔N形装甲板的弹道极限，即767.5 m/s。

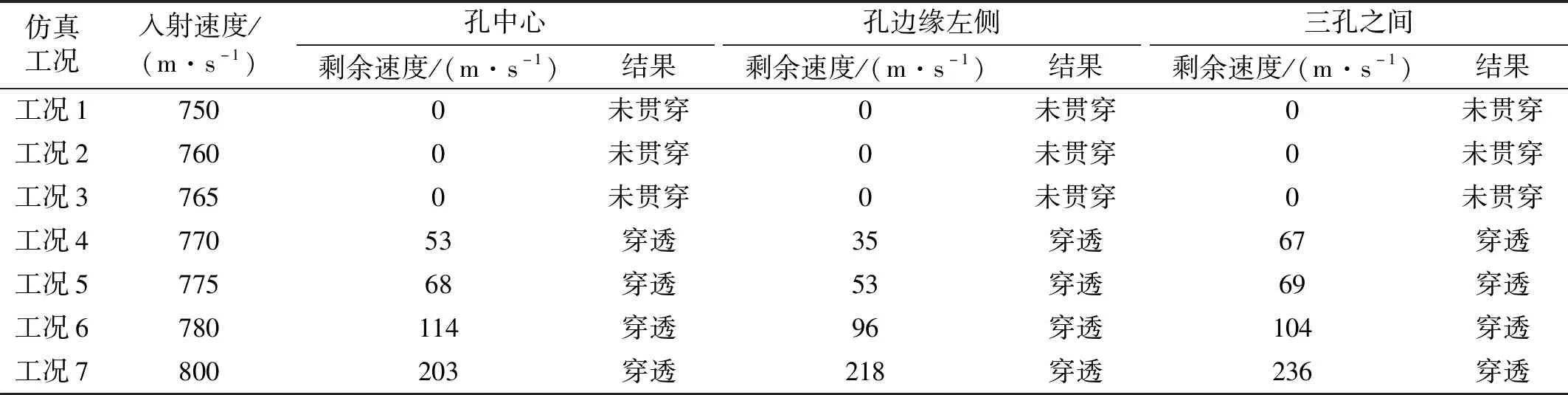
表6 钢芯侵彻锥形孔N形装甲板仿真结果Tab.6 Simulation results of steel core penetrating conical bore N-shaped armor plate

为进一步评价锥形孔N形装甲板的抗弹性能，对与其材料相同的等质量高强钢均质靶板抗穿甲弹钢芯侵彻过程进行数值模拟。均质靶板平面尺寸与N形装甲板一致，即边长50 mm；均质靶板厚度为7.77 mm，钢芯垂直入射靶板中心点。钢芯侵彻等质量均质靶板的数值模拟结果，如表7所示。由表7可知：等质量均质靶板的弹道极限在680～685 m/s，取平均值682.5 m/s为均质靶板的弹道极限。可以得出：与等质量均质高强钢板相比，锥形孔N形装甲板的弹道极限值提高了12.5%，抗弹性能更优。

表7 钢芯侵彻等质量高强钢均质靶板仿真结果Tab.7 Simulation results of steel core penetrating homogeneous high strength steel target plate of same weight

3 结 论

研究了可用于军用车辆弹道防护的N形结构装甲板的抗弹性能。通过数值模拟分析了N形装甲板的抗弹侵彻机理，研究了弹着点位置与孔构型对其抗弹性能的影响，并与等质量均质钢板进行了对比，所得结论如下：

(1)N形装甲板可同时利用孔板的边缘效应和斜板的倾角效应抵御穿甲弹侵彻；孔板可有效破坏被覆层并折断钢芯，斜板使钢芯进一步剪切破坏并碎裂。

(2)不同弹着点下N形装甲板的抗弹性能不同；相同入射条件下，当弹着点位于孔边缘上侧时，贯穿后钢芯剩余速度最低，动能损耗最大。

(3)在500～850 m/s弹速内，锥形孔板可使子弹在侵彻过程中持续受到侧向力作用而发生较大偏转和破坏，相比方形和圆形孔板，被贯穿后子弹剩余速度更低。

(4)与等质量均质高强钢板相比，锥形孔N形装甲板的弹道极限值提高了12.5%，抗弹性能更优。