基于局部地球重力场模型的常梯度声线跟踪水下定位方法

汪剑云

（重庆市勘测院，重庆 401121）

0.引言

在海洋探测过程中，水下定位是重要的环节之一，在各种海洋工程建设中得到广泛应用[1]。由于电磁波遇水具有快速衰减的特点，所以常用于定位系统中的全球导航卫星，无法在海洋中发挥作用。因此，在水下定位研究中，声波的传播特点开始成为研究核心[2]。由于水体压力、温度等介质条件的影响，使得声波传播的速度并不均匀，声波在传播过程中不再是直线形式，而是具有一定弯曲程度的曲线，而声线的弯曲程度影响着最终水下定位的准确度[3]。采用常梯度声线跟踪方法对声线进行追踪，以确保定位误差的减小。在实际应用中，传统定位的误差随着时间的递增而不断积累。因此，需要定期通过一些技术进行校准和修正。辅助校正工具一般都是匹配算法实现定位方法的校正，但是在具体实践中受到不同定位环境的影响依旧会有较大的误差[4]。针对这一问题，本文提出以观测重力为基础，通过局部地球重力场模型完成水下定位，这种新的方式只需要通过重力异常，与目标区域经、纬度坐标就可以进行定位。因为在观测重力中包括目标的位置坐标信息[5]，利用非线性滤波方式，可以实现精准定位。通过本文研究降低了水下定位误差[6]，促进海洋建设行业发展。

1.常梯度声线跟踪水下定位方法设计

1.1 声速剖面分析

声速作为水下定位的重要参数，受到很多因素的影响。通常情况下，随着水深变化声速值大小也会改变，这种变化趋势可以通过剖面结构得以展现。即便在同一时间，在不同空间位置上受到洋流运动的作用，海水中的声速剖面结构时刻都会发生改变。所以，在水下定位方法设计中，通过声速剖面误差的控制，提升水下声学定位精度。所以，在定位过程中需要针对声速剖面数据进行分析。在分析过程中可以应用几种声速经验模型（如表1所示）：

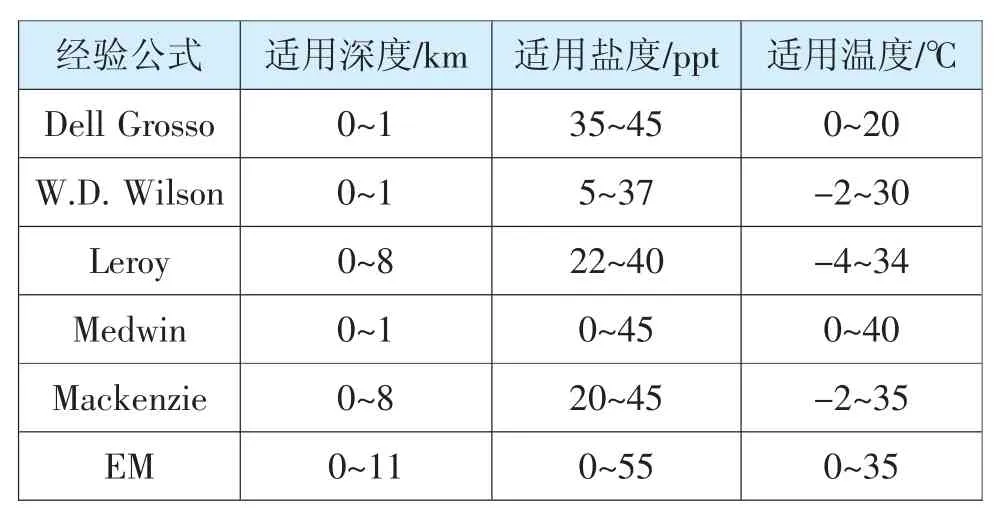
表1 水下声速经验模型公式对比

表1所述的声速经验模型公式从不同的时间被研究出来，其适用条件也各有差异。在声速值计算过程中，需要依据现有条件，选择与之匹配的公式进行声速剖面分析，从而获取最佳声速经验模型[7]。在实际应用中，声速剖面的分析需要以Argo实测数据为基础[8]，该项资料可以通过资料中心获取。研究发现以上几种经验模型公式中，Dell Grosso模型在海水较深的环境下获取的声速值偏高，所以证明Dell Grosso模型不适用于声速计算。其余模型均可满足声速剖面分析需求。与常规方法不同，本文在确保计算精度的同时，采用简单声速剖面进行计算，其计算流程（如图1所示）：

图1中，X为水平位移；X′与△X分别为目标坐标初值和目标求解坐标改正量，以当前水体环境为依据，采用计算模型完成声速剖面分析。

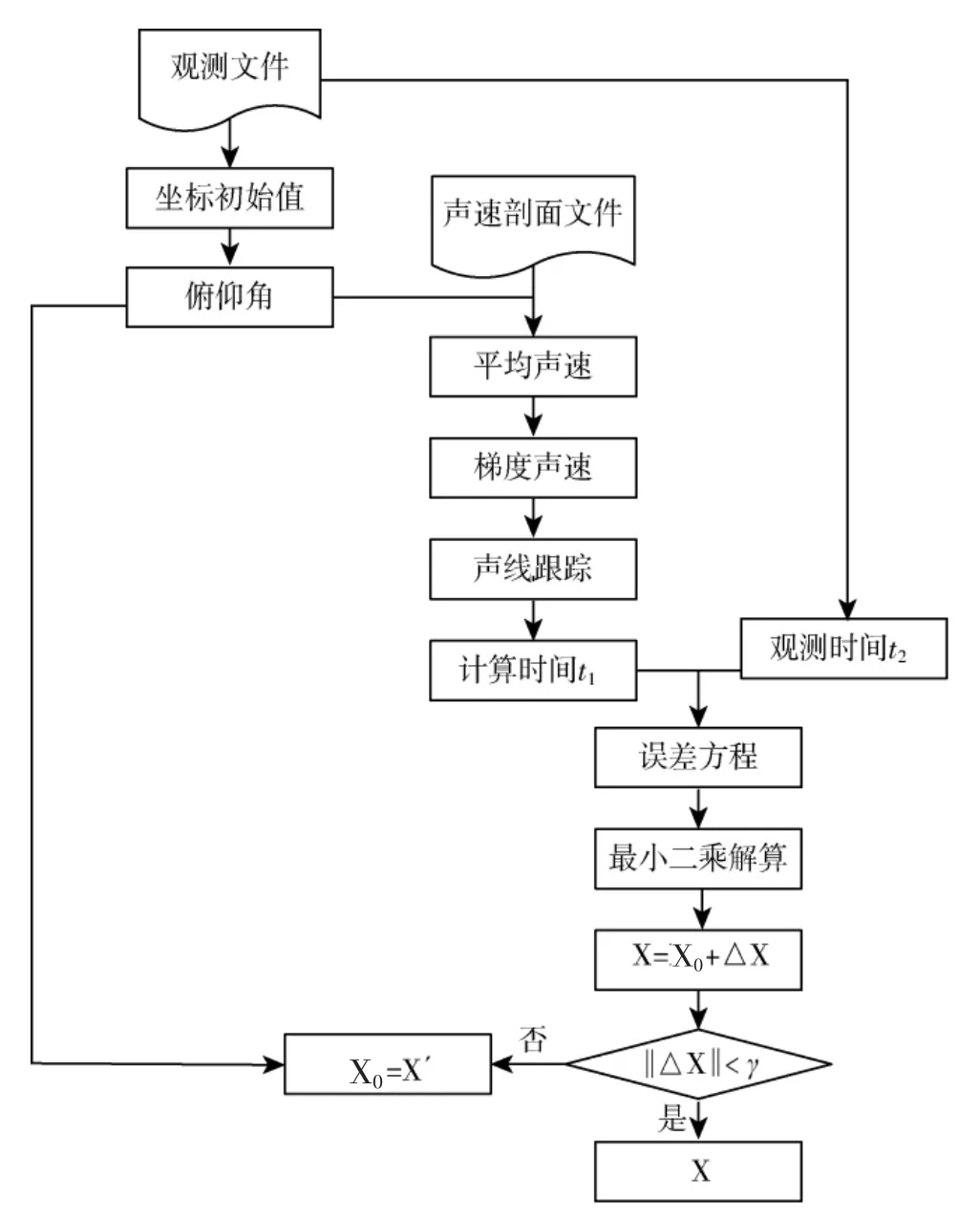
图1 声速剖面法计算流程图

1.2 设计常梯度声线跟踪方法

通过声速剖面分析获取的声速值，由于介质的影响存在较大误差[9]。在声学定位中，一些外界因素的存在使得声线在传播过程中路径是弯曲的（如图2所示）。当水越深时声速变化较大，随之增大的就是声线的弯曲程度。

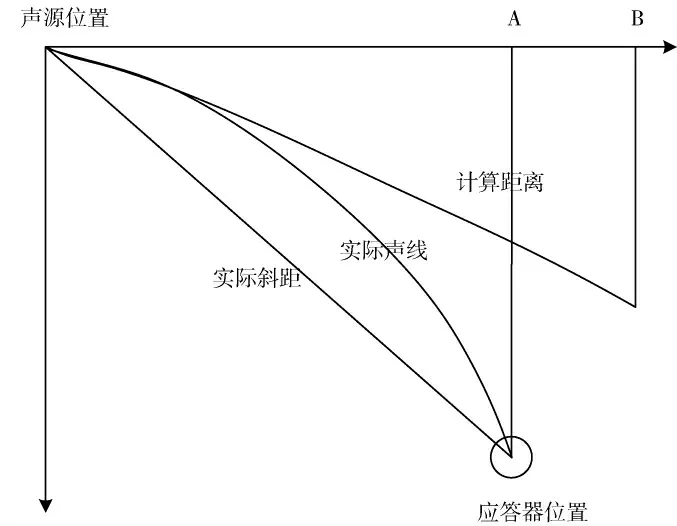
图2 声线弯曲示意图

从图2可以发现，因为声线弯曲改变了位置。A点为应答器实际投影位置，但是当受到声线弯曲的影响后，传播路径发生改变，应答器位置投影显示为B点，从而造成计算结果的误差。在声线弯曲影响下造成的误差结果，就是AB之间的距离差。在水下定位精度判定中，声线弯曲率半径越小，造成的精度误差越大。为了保证定位结果的准确程度在可接受范围内，利用声线跟踪算法进行声线跟踪，实现声线弯曲影响程度的降低。

采取声线跟踪方法提升定位准确性。在水下定位时，受到海水特性影响声速不断变化，声线也会出现折射弯曲。因此，在定位过程中为了避免产生误差太大，需要采用声线跟踪技术对声速误差进行补偿，同时提高定位精度。海水中声波的传播与光的折射相似，同样遵循snell法则（如图3所示）：

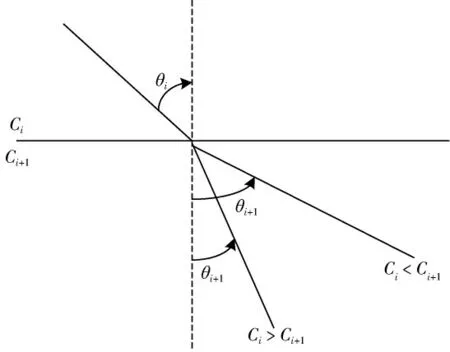
图3 Snell法则示意图

图3中，Ci、Ci+1为相邻海水层表面的声速值大小；θi和θi+1是海水界面声波信号的折射角和入射角。当声信号入射角不等于0时，声波信号在海水界面处，在经历N次折射以后，实际的声波信号的传播路径为一条折线。利用常梯度声线跟踪方法将声速剖面进行分层，如果层内声速是依据常梯度的形式变化，那么就使用层追加的方式获取声线垂向距、侧向距与传播时间（如图4所示）：

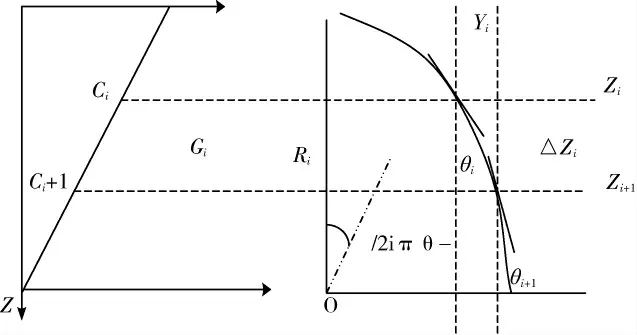
图4 分层等梯度声线跟踪示意图

图4中，分层等梯度声线跟踪情况，倘若将等梯度水层设置为N，那么i为其中某一层，该层的声速梯度Gi计算如式（1）所示：

式（1）中，△Zi为i层的水深度；Ci+1为第i+1层的声速，依据Snell法则将声线跟踪示意图中的声线轨迹半径设置为Ri并且图中的θi与θi+1为入射角，其表示的是第i层、i+1层的声线信号入射角。则声波在当前水层弧长计算如式（2）所示：

那么经历该弧段的时间计算公式如式（3）所示：

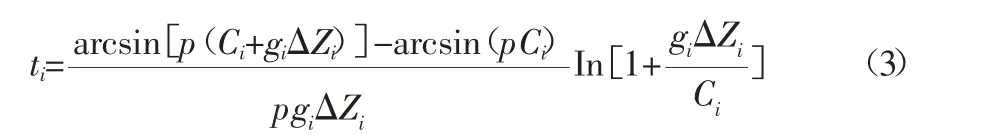
本文设计的常梯度声线跟踪方法在应用中呈现出的信号传播路径，和真实传播路径基本保持一致，具有较高的定位解算精度。

1.3 构建局部地球重力场模型

以地球重力为基础进行定位的方法，观测重力与目标之间的位置关系是重力场模型运用的核心。为了提升局部地球重力场模型的应用，最近几年开始在测量领域不断研究，构建了以傅立叶变换为基础的局部地球重力场模型，并将该模型推广应用。模型中首先进行扰动位的计算，其平面公式如式（4）所示：

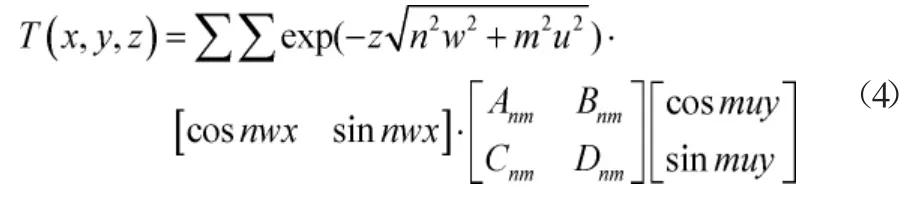
式（4）中，m、n为两个任意的非负整数；而w和u则为圆频率。此外将待定系数用Anm、Bnm、Cnm、Dnm来表示。将已知区域设置为［-N＜x＜N，-M＜x＜M］，根据该区域的重力异常可得到傅立叶级数如式（5）所示：

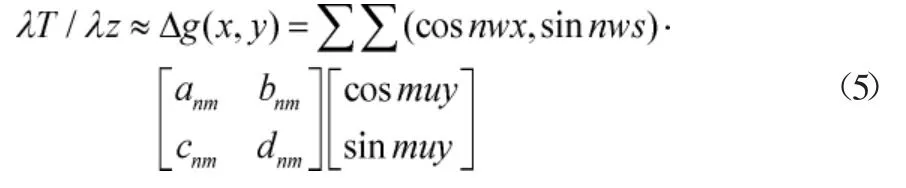
傅立叶系数如式（6）、式（7）所示：

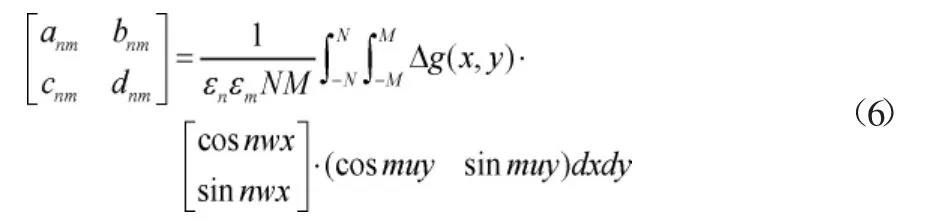
并有

根据式（7）得出的傅立叶系数结果，获得傅立叶级数，从而得到公式（4）所求的平面解析结果，明确局部重力异常定位。除此之外，在计算过程中重力异常是以周期函数的形式存在，有一些重叠误差存在，所以通过周期延拓的方式达到最佳效果。周期延拓处理方法也就是添零，本文利用50%添零比例，简单来说就是依据重力异常分布范围的1.5倍，获取傅立叶系数。

因为局部重力场模型在应用中，与大地经纬度坐标存在着相对应的联系。所以，依据需求促使模型精度提高到一定范围内，局部重力场模型就可以在水下定位方面起到良好的效果。由于通过观测重力进行定位要求量测方程精度较高，因此，局部重力场模型的分辨率也要达到较高条件。针对本文构建的局部重力场模型，进行验证。采用本文所述的模型针对某一具有重力异常数据的区域进行计算，将计算结果与真实重力异常值相比较，其结果（如表2所示）：

通过表2所呈现的计算值和真实值精度比较结果，可以发现二者之间差值不大，基本可以保持一致，证明采用局部地球重力场模型可以获得误差较小的水下目标位置。

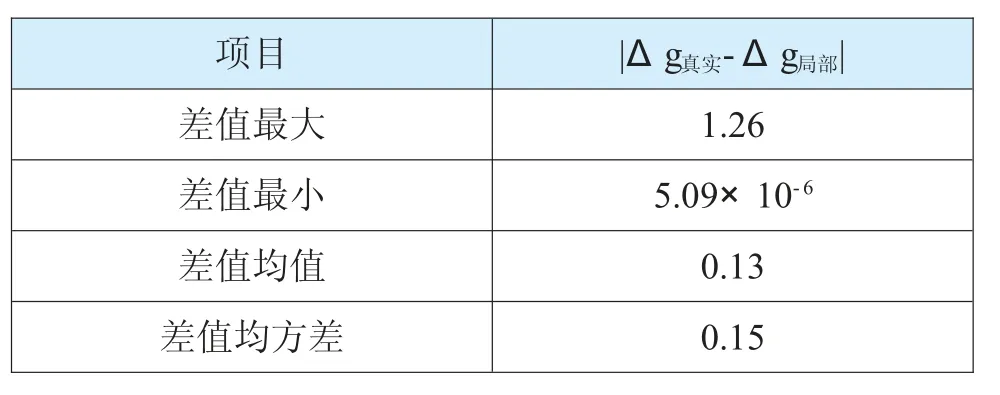
表2 计算值和真实值精度比较

1.4 确定水下目标位置

为了更好地确定水下目标位置，建立目标状态方程如式（8）所示：

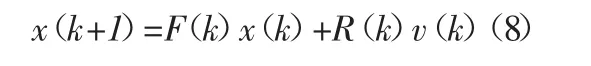
式（8）中，k为时刻；F（k）和R（k）为该时刻的目标状态、扰动矩阵；v（k）为表示零均值过程白噪声大小。则如公式（9）所示：

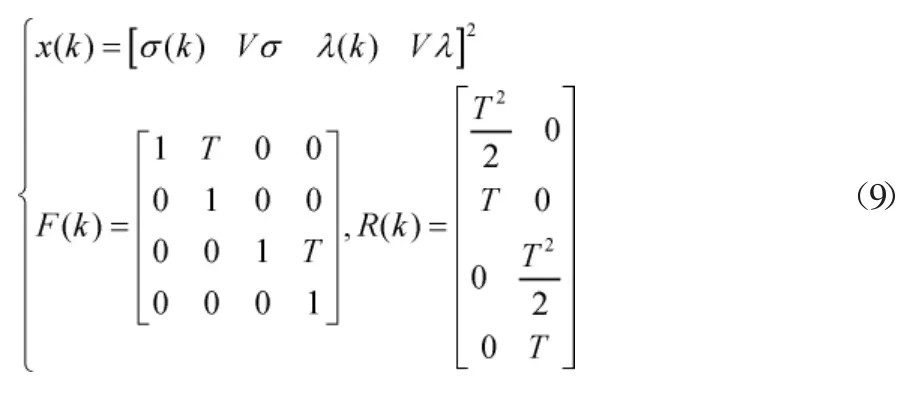
式（9）中，k时刻的目标经纬度用σ（k）和λ（k）来表示；Vσ和Vλ分别为水下目标的运动速度；T为采样间隔。以局部地球重力场模型，结合常梯度声线跟踪方法建立一个非线性量测方程。采用扩展卡尔曼方式进行滤波降低定位误差，并且对测量方程进行泰勒展开的线性变换。

针对测量方程采用优化后的最小二乘优化定位法进行求解。通过最小二乘法确定目标大概位置信息，之后利用牛顿迭代法对结果进行迭代优化，获取最优的水下定位信息。并且当初始值满足精度条件的范围要求时，可以将迭代次数减少，从而快速获取量测方程的解，提高水下定位效率。

2.实验

为验证本文定位方法的有效性和实用性，进行了模拟仿真实验。在软件中模拟声线跟踪技术，并且采用Munk声速剖面呈现出一系列变量值。进行实验之前，预先分析了本文设计方法的声线跟踪效率，选择水深为50m、100m、200m、500m、1000m、5000m的区域进行测试。同时选用两种常规定位方法进行处理，不同方法的计算耗时（如表3所示）：

根据表3中计算时间的比较可以发现：随着水深的增加声线跟踪计算耗时处于不断增长的状态。然而，可以明显得出本文设计方法耗时相对较少，直到水深达到5000m时约为1.98s以下，两种常规方法此时耗时分别为2.25s、2.30s。三种方法的应用都可以满足常梯度声线跟踪水下定位的需求，本文设计方法有效保证了工作效率。

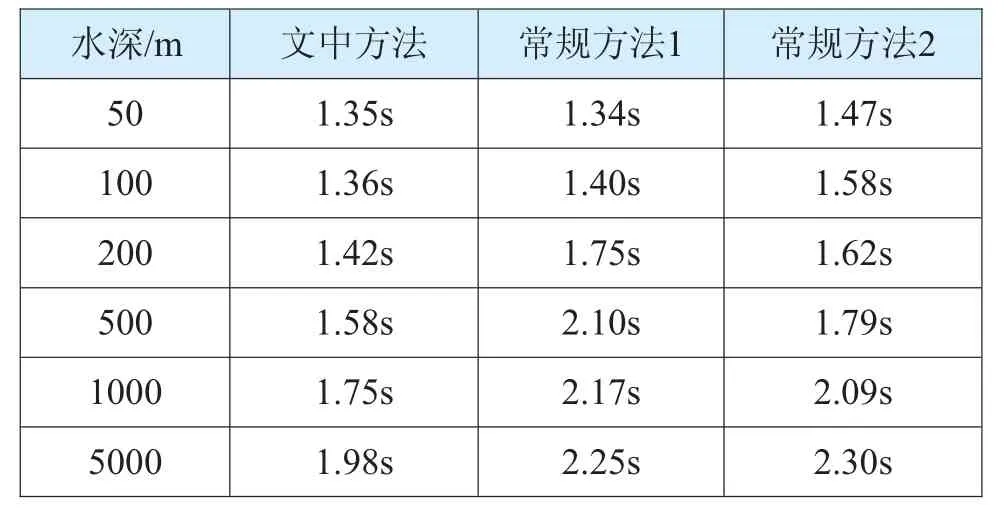
表3 声线跟踪计算耗时

2.1 水深50m时定位结果分析

在水深保持为50m的实验环境下，应用本文设计方法和两种常规方法进行定位实验，其x、y、z三个方向的定位误差（如图5所示）：

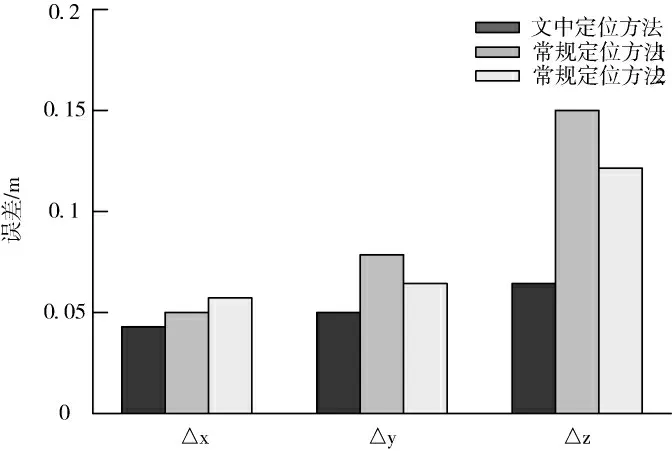
图5 水深50m时定位误差对比

从图5中可以发现：应用文中设计的定位方法后，目标定位的x、y、z三个方向误差相比常规方法都有所降低。其中，以z方向最为明显，文中设计方法的误差约为0.07m，而两种常规定位方法的平均误差分别为0.15m、0.12m。通过对平均误差进行计算可知：本文定位方法的平均误差相比其余两种定位方法分别降低了43%、36%。

2.2 水深100m时定位结果分析

通常情况下，随着水深的不断增长，水中目标定位结果的误差会产生巨大变化。因此，选择水深保持为100m区域，再次进行同样的实验，实验结果（如图6所示）：

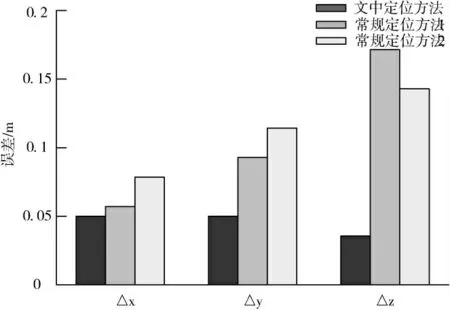
图6 水深100m时定位误差对比

通过观察可以发现：随着水深增加两种常规定位方法的误差均有所增大。但本文设计方法受到的影响几乎可以忽略不计。经过计算得出文中定位方法的平均误差约为0.05m，常规方法1与常规方法2的平均误差约为0.12m、0.11m。因此，在水深为100 m时，本文方法将定位平均误差降低了58%、55%。综上所述，本文设计定位方法有效降低了定位误差，并且随着水深的递增，该项优势越发明显。

3.结束语

本文以局部地球重力场模型为基础，设计了一种新的常梯度声线跟踪水下定位方法。通过本文的研究，提升了水下定位精度，与常规定位方法不同，避免受到周围环境的影响产生误差。通过本文的研究结果，促进了常梯度声线跟踪的研究和进一步发展，未来也会针对定位误差继续深入研究。