曲面网壳钢结构工程施工测量技术

王登杰 王 岩 熊长鑫

（1.山东大学土建与水利学院，山东 济南 250061；2.山东高速基础设施建设有限公司，山东 济南 250013）

0.引言

大跨度钢管桁架屋盖作为一种曲面网壳钢结构形式，在国内外大型场馆的建设中的应用越来越多。由于此类工程在结构上是空间曲面网壳钢结构，施工过程中的空间结构内力与体系转换后的空间结构内力相差十分悬殊，施工误差及结构变形对结构的刚度和安全稳定作用具有重大影响。因此，如何通过准确的施工测量降低安装误差，控制安装精度，提高安装质量，是钢管桁架结构工程施工的一个关键环节[1]。

在施工测量方面，钢管桁架屋盖结构与一般混凝土结构的方法不同，混凝土工程施工测量是在相对稳定的施工作业面上进行精密定位测量，而钢管桁架屋盖结构施工定位，是在空中进行三维跟踪测量定位和精密测量连续归化校正定位，通过不断定位与调整，使每一段钢管桁架精确定位，组成的每榀桁架位置正确、线形完美，并符合设计及规范要求。因此，钢结构安装的精密定位及测量校正技术是钢结构工程施工的重点，也是施工测量的难点。同时，曲面网壳钢结构的每榀桁架在不同结构层上倾斜角与扭转的方向都不相同，而且每榀桁架结构之间也没有规律可循，使得确定桁架结构的定位数据计算过程非常繁琐[2]，给精密定位测量带来大量内外业工作。特别是在地面上安置全站仪，在施工控制点上直接观测到每榀桁架的端点（已知坐标的放样点）是非常困难的。在实际的放样过程中必须重新计算桁架上能看到的点（管桁架的上缘线或下缘线上的点），以现场能看到的点作为放样点，来进行精密定位和测量校正。这样给现场计算放样点的坐标和传统的定位测量带来了许多的困难。

传统的测量方法，是采用极坐标法确定放样点的平面位置，利用水准测量或三角高程测量方法来测量放样点的高程。也就是在布设好的控制点上安置全站仪，采用空间三维极坐标的方法，通过测设每节钢桁架端点的坐标来确定放样点的位置。但是，由于钢结构施工场地狭小，对测量控制点间通视影响较大的特点，这种传统的测量方法很难保证相邻控制点之间及控制点与放样点之间的通视，使得传统的测量方法在曲面钢结构施工测量及精密定位中无法应用。为此我们提出了基于空间直线方程的归化法放样。

1.高精度控制网的建立与快速加密

施工测量主要是为工程建设提供技术成果和技术服务。施工测量的精度与质量直接影响整个工程建设的安全和质量[3]。根据曲面钢结构工程精密定位的要求，结合济南市自行车比赛馆实际情况，利用高精度的全站仪（TCR1200+）和精密电子水准仪（Dini 12）建立了高精度的三维首级控制网（如图1 所示）,在比赛场馆的中心设置一固定点为多边形的中心点，利用此中心点增加图形强度和网形结构。通过测量所有的边长和角度，形成边角混合网，使首级控制的精度达到二等三角网的技术要求，同时满足曲面钢结构工程体系转换时的变形测量要求。在每一个控制点上设置强制对中装置，其高程采用Dini12 电子水准仪进行精密水准测量，使其精度达到国家二等水平测量技术要求[4]。济南市自行车比赛馆，在施工初期就建立了高精度的三维首级控制网，它不仅是钢结构工程施工的首级控制网，还是曲面钢结构工程变形测量的控制网。

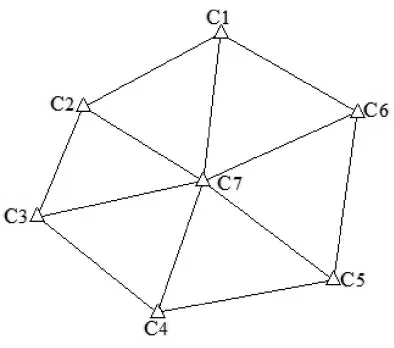
图1 施工控制网

由于受到施工条件和环境的限制，在施工放样时需要快速加密控制点。以方便曲面钢结构的精密测量与定位。快速加密控制点是利用全站仪（TCR1200+）的自由设站功能，通过后方交会法，可以灵活、快速加密施工控制点（如图2 所示）。将全站仪安置在P 点上，观测P 点至C1、C2、C3各方向的夹角γ1、γ2。根据已知点C1、C2、C3坐标，即可推算P 点坐标。后方交会的计算工作量较大，计算公式很多，在此不再详述。利用此加密控制点即可进行钢结构的施工放样和精密定位工作。

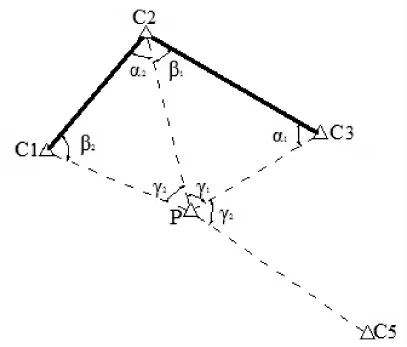
图2 后方交会示意图

2.似水准法高程测量

曲面钢结构工程大部分是空中定位的，放样的点离地面很高，受施工条件和施工环境的限制，传统的水准测量根本无法进行，只能采用三角高程测量方法。传统的三角高程测量方法，是将全站仪安置在控制点上，通过观测仪器到放样点的距离和竖直角度，来求得放样点的高程[5]。

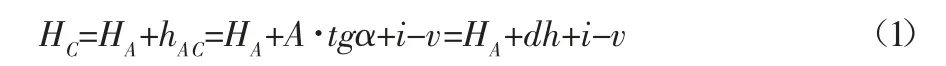
式（1）中，D 为仪器到观测点的水平距离；α 为竖直角；i为仪器高；v 为棱镜高；hAC为A 点到C 点的高差。

传统的三角高程测量的方法，有以下不足：（1）由于是间接测量高程，即要量取仪器高还要测量棱镜高，影响测量精度的因素多，带来的测量误差大，放样点的测量精度低；（2）由于施工条件和周围施工环境的影响，控制点上的全站仪很难看到放样点上棱镜，使高程测量常常无法进行。为此，我们提出了似水准法的高程测量。似水准法高程测量，就是将全站仪安置的控制点（水准点）与放样点之间的任意位置A 点上（只要A 点能与放样点和任意控制点通视），通过测量仪器到控制点C 的高差和仪器到放样点P 的高差，利用控制点C的已知高程，即可得到放样点P 的高程（如图3 所示）：

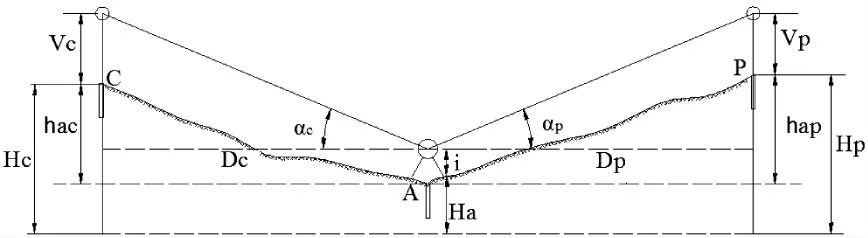
图3 似水准法高程测量

由式（2）可知，仪器到控制点C 的高差为hAC，则：

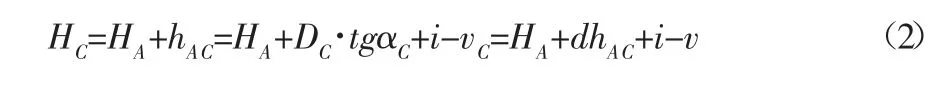
式（2）中，Dc为仪器到控制点的水平距离；αc为仪器到控制点的竖直角；i为仪器高；vc为控制点C上的棱镜高；dhac为仪器到控制点的高差读数，称为“后视读数”。

同理，仪器到观测点（放样点）P的高差为hAP，则：

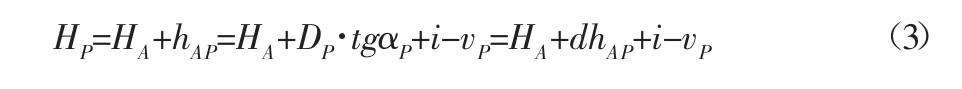
式（3）中，Dp为仪器到观测点的水平距离；αp为仪器到观测点的竖直角；i为仪器高；vp为观测点上的棱镜高；dhap为仪器到观测点的高差读数，称为“前视读数”。

由式（2）和式（3）得：

由式（4）可知：当控制点与观测点上的棱镜高相同时，即vc=vp时，控制点C点与观测点P点的高差hCP=Dc·tgαc－Dp·tgαp=dhac－dhap，即高差=后视读数-前视读数，与水准测量相似，这就是似水准法的计算公式。

由式（4）可知：由控制点高程HC计算观测点高程HP时，与全站仪的仪器高i值无关。观测高差的精度只与仪器到控制点和观测的距离和竖直角有关，这与全站仪的测角精度和测距精度有直接联系。如果采用测角精度为1"，测距精度为1mm+1ppm 的TC1200+全站仪进行观测，观测距离不超过200m时，其实测高差的精度可达到±2 mm以内[6]。其精度远远满足钢结构工程施工放样的要求。

3.基于空间直线方程的归化法放样

3.1 建立空间直线方程

钢结构工程深化设计时，给出的坐标是每段管桁架结构中每根钢管两端点的中心坐标（即管轴线坐标），根据此段钢管的上、下两端点的中心坐标，可以建立钢管的中心线方程（如图4所示）：

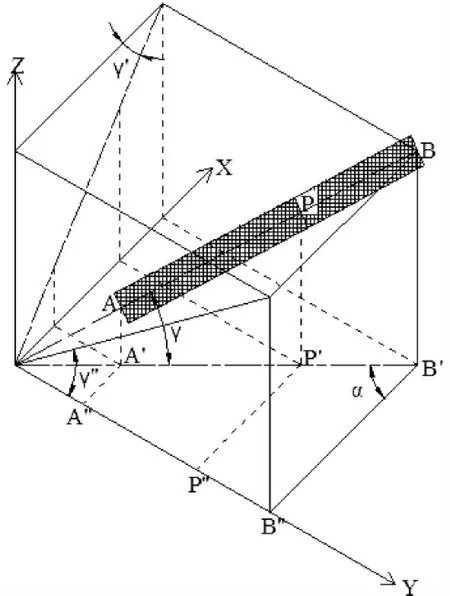
图4 缘线上点的坐标计算

3.1.1 建立计算模型

钢结构施工时，施工放样坐标是由深化设计单位提供的每段管桁架中某根钢管轴线两端点的空间三维坐标，即A、B两点的坐标，分别为A（xA，yA，zA，）和B（xB，yB，zB，）（如图5所示）。γ是钢管轴线与XOY面的夹角，即钢管的轴线与钢管轴线在XOY面上的投影线A′P′的夹角；γ′是钢管轴线在XOZ面上的投影与X轴的夹角；γ″是钢管轴线在YOZ面上的投影与Y轴的夹角；α为钢管轴线在XOY面上的投影与X轴正方向的夹角，即钢管轴线AB的方位角；P为钢管轴线上的任意一点，离端点A的距离为l，R为钢管的半径。

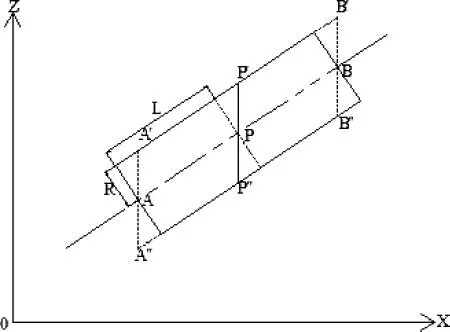
图5 计算模型

3.1.2 建立直线方程

由图5可知，xA、yA和tgγ′、tgγ″是此段钢管中心线分别向XOZ面和YOZ面投影线的截距和斜率，由此，可归纳出钢管中心线及在XOZ面和YOZ面投影线的空间直线方程为：

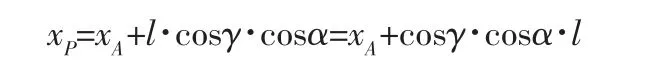
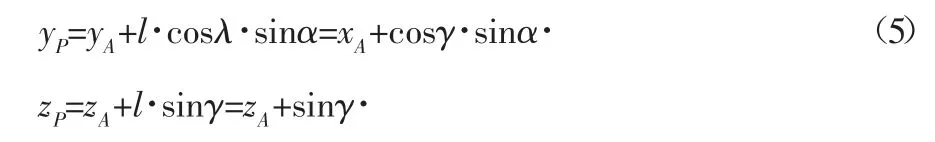
式（5）中,l为钢管轴线上任意一点P到A点的距离；对于每段钢（管）桁架来说，α和γ是定值，式（5）即为钢管轴线空间直线方程，它们是l的函数。当给定一个P点后，l值即可确定，即可计算P点的坐标（xP，yP，zP），用实测坐标与计算坐标比较，可以求得坐标差（ΔxP，ΔyP，ΔzP），通过过渡点修正这一差值，将P点调整到正确的位置，使坐标差为零，即可精确放样P点的位置，经过多次观测、归化、调整，得到P点的精确位置。

在实际工程的测量时，因为A、B、P点位于钢管的轴线上，是无法放置棱镜。因此，在实际工程放样时，要将钢管轴线上的点引到钢管的上缘线或下缘线。上缘线上的P′点沿上缘线到A端上缘线点的距离为（l+R·tg）γ，下缘线上的P″点沿下缘线到A端的下缘线端点的距离为（l－R·tg）γ，则上缘线上P′点的坐标（xP′，yP′，zP′）为：

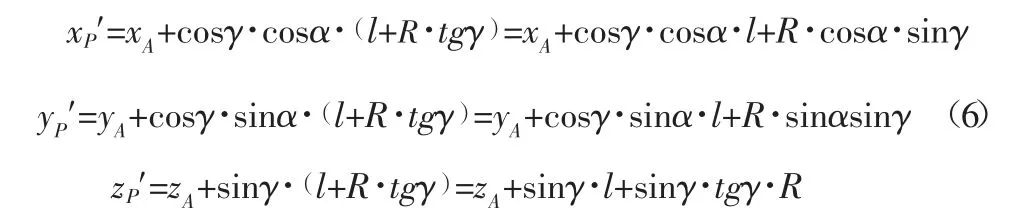
同理，可得下缘线上P″点的坐标（xP″，yP″，zP″）为：

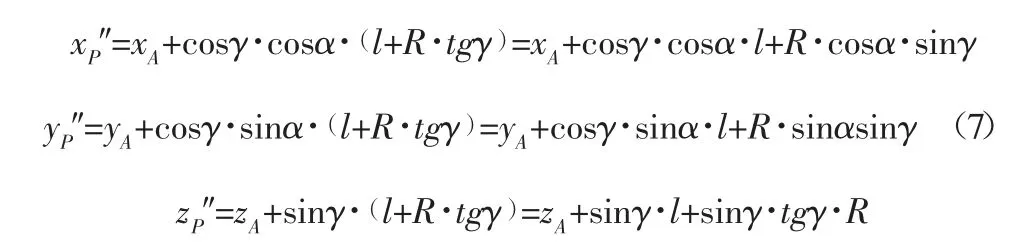
式（6）和式（7）即为上缘线和下缘的空间直线方程。

3.2 归化法放样测量

钢管桁架的精密定位是按照先放样、后安装、再测量调整的归化法放样程序进行的[7]，首先采用式（7）计算下缘线上特征点坐标，计算下缘线上A″、B″两点的三维坐标，采用三维空间极坐标法，将A″、B″两点放样在固定钢管桁架结构的临时支架上，如果放样的点位恰好不在支架上，此时，可以在此处的临时支架上焊一块小钢板（此钢板能方便调整），将要放样的点A″或B″测设在此钢板上，精度满足要求后并固定此钢板。

然后吊装钢管桁架结构并进行安装，安装时将钢管桁架结构上A″、B″两点与放样好的临时支架上的A″、B″两点对接，对接好后并临时固定。然后通过测量钢管桁架结构（钢管）上缘线上的A′、B′两点的坐标，与计算的设计坐标比较，求得坐标差，根据A、B两点的坐标差，来进行归化调整钢管桁架结构，使实测的A′、B′两点的坐标与设计坐标一致。

在放样和校核测量过程中，当看不到上缘线上的A′、B′时（此时下缘线上的点已经无法看到），可以将棱镜放到上缘线上的任意一点P′上，通过似水准测量的方法，精确地测量出此点的高程zP′。将zP代入式（7）中的zP′坐标计算公式，可反求出此点的l。然后。将l代入式（7）中，可求得此点的（xP′，yP′）与实测的（xP′，yP′）进行比较。根据坐标差进行归化与调整，直至坐标差满足要求为止。

4.结束语

本文创造性地提出了中间设站的三角高程测量和基于空间直线方程的归化法放样，很好地解决了施工放样过程中测量与施工安装相互干扰的矛盾，加快了施工放样和测量校核的速度，提高了测量精度。经工程竣工验收可知，采用本方法进行施工测量，其平面放样误差平均±3.5mm，高程误差平均±3.0mm。钢桁架结构安装误差均满足允许误差±3mm～±5mm要求[8]。

在曲面网壳钢结构施工测量及精密定位过程中，对部分在施工控制点能直接看到的特征点进行了对比测量。对放样的点进行精密观测，实际观测坐标与设计坐标比较，最大相差±1.0mm，高程最大相差±2.0mm。观测点的坐标中误差为±0.69mm，高差中误差为±0.83mm，均达到了亚毫米级的观测精度。

空间直线方程是将空间曲面钢结构工程的不规则性、多样性、复杂性简化为由短直线组合而成。这与实际的空间曲面结构的坐标计算略有不同，但这种差别与钢桁架结构的加工误差相比，是可以忽略的。如果能将其归化成曲线方程，其精度更高，与实际工程更接近，这正是我们以后研究的方向。