基于转向角变换的智能转运叉车运动规划研究*

霍旭坤,马晓录*,刘 艳,吴立辉

(1.河南工业大学 机电工程学院,河南 郑州 450001;2.湖南迎春思博瑞智能装备有限公司,湖南 宁乡 410006)

0 引 言

在大中型企业、仓库、码头等场所,常需要将货物从码垛或卸货点转运,并装载到大型运输车辆上。以往采用人工叉车时,用工成本高且工人存在安全隐患。

有企业提出了无人化、智能化转运装载需求。在非结构化环境下,无人驾驶运载车辆作业正在活跃地进行[1],货车停放位姿具有不确定性,在叉车运载箱、包到达装载区域后,需要对车身位置和航向进行调整,以对准登车桥,才能准确驶上货车车厢并完成装载。叉车属于低自由度的大吨位车辆,在调整航向时应尽量避免原地打转、频繁启停、倒车等复杂动作。应用运动规划技术可使叉车仅用简单动作就准确调整位置和航向的需求,因此,对智能转运叉车的运动规划进行研究很有意义。

解决智能转运叉车的自动驾驶运动规划问题有3个层次:(1)搜索最佳路径;(2)搜索最佳机动动作;(3)搜索最佳轨迹。解决方式可归纳为两种方案:(1)忽略时间,只考虑二维空间的路径规划;(2)考虑时间因素,在三维时空进行的运动规划。

屈盼让等[2]提出了基于B样条曲线解决无人车路径规划问题的方法,建立了完整的分步规划模型。吕恩利等[3]采用四次五阶准均匀B样条曲线,分前后段合并生成满足叉车多约束条件下的避障路径。周兵等[4]提出了一种基于非均匀B样条曲线,且满足多约束要求的路径规划方法。吕恩利等[5]提出了基于三次均匀B样条曲线的托盘拾取路径规划方法。王国辉等[6]提出了一个用于自动驾驶车辆运动规划的时空网络模型,该网络利用采集的时空信息产生转向运动反应。KHESRANI S等[7]提出了一种解耦的路径-轨迹规划方法,引入了模糊平坦度的概念,以保证在不同不确定性条件下规划任务的准确执行。

路径规划需要路径跟踪算法控制行车动作予以配合,不仅需要复杂的计算,还可能出现行车动作的快速变换,如急转、急加速等情况,而这些情况在实际行车中可能会受到车辆本体机械结构的限制[8]。运动规划是根据特定场景特点和车辆参数建立的,只需要简单地控制动作参数即可完成轨迹跟踪,针对性强。常见的运动规划方法有轨迹预测[9]、泛函梯度优化[10]、多项式插值[11]等。

结合真实货场装载场景,为实现智能转运叉车的自主登车,提高叉车在箱、包转运装载过程的灵活性和功能性,本文以具有非完整约束的智能转运叉车为研究对象,综合考虑各种约束条件,建立智能转运叉车运动规划模型,并根据车辆和装车场景数据求解该模型运动控制参数,生成车辆行驶轨迹,验证到达登车点时车辆航向的准确性以及控制过程的可行性。

1 智能转运叉车作业

在半结构化箱、包装载环境下,货车停放在指定的装车区域内,叉车作业的整个流程如下:

智能转运叉车从仓库拾取托盘,通过调度系统得知目标货车的停放区域,经全局路径规划行驶到装载区域目标货车登车桥后方一定的距离,启动登车桥位姿识别算法,通过传感器进行登车桥位姿识别以及叉车自身位姿识别,根据识别到的登车桥相对位姿启动运动规划算法,得到智能转运叉车行车动作控制参数,进而通过控制系统跟踪行车,完成调整航向和位置的目标。

登车前位姿调整作业流程如图1所示。

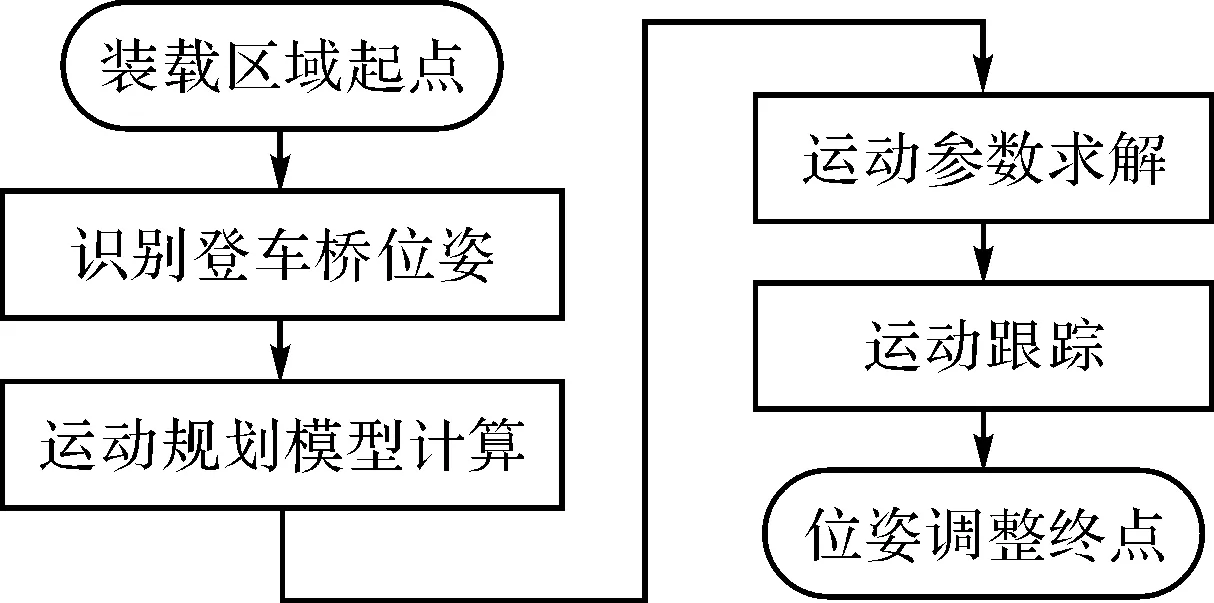
图1 智能转运叉车位姿调整作业流程

在叉车动力学研究中,叉车稳定性问题通常用横摆角速度的变化规律来描述,而叉车轨迹保持问题通常用侧滑角的变化规律来描述[12]。

针对叉车侧偏角难以直接测量的问题,ZHANG Xu[13]提出了一种仅采用横摆角速度反馈的叉车主动转向系统设计方案,提高了叉车的转向稳定性以及操纵稳定性。研究叉车运动规划问题常忽略动力学和其他微分约束,主要关注车辆的转向和位移[14]。

叉车属于前轮驱动、后轮转向的非完整性约束车辆,因此此处以前轴中心点为车辆坐标系原点建立右手坐标系,并将识别到的登车桥尾板位姿作为目标点,根据在二维平面内生成一条从起点到终点的可行路线轨迹,再运用逆运动学方法得出决策动作的参数。

不同位姿下的运动规划算法生成的行车轨迹如图2所示。

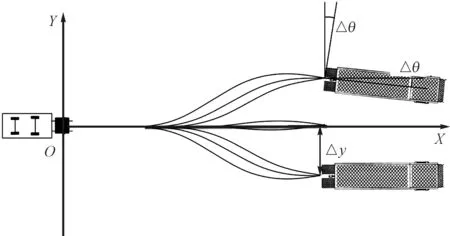
图2 不同位姿下的运动规划算法生成的行车轨迹

2 智能转运叉车运动约束

登车运动规划的目的是使得智能转运叉车能实现自主登车。智能转运叉车运动规划以匀速前进和匀转向角速度为基础,建立分阶段运动的运动模型,通过控制每个阶段持续的时长、速度、角速度,确保智能转运叉车到达目标位置且终点航向角准确[15],使该运动规划模型生成一条可供智能转运叉车跟踪的行驶路径。

2.1 智能转运叉车运动学模型

智能转运叉车的结构方式是后轮转向前轮驱动,阿克曼转向机构在实际转向时后轮内侧轮胎转角偏大。在建立智能转运叉车运动学模型时,假设叉车车体为刚体,忽略不计车轮形变,在后轴中心设一个等效转向轮,在前轴中心设一个等效驱动轮;假设理想状态下所有车轮作纯滚动而无滑移,且转向时无侧滑。

以前轴为原点建立的运动学模型如图3所示。

在全局坐标系XOY下,(x,y)为前轴轴心坐标,P为转向中心。在前轴轴心处,根据运动学约束可得:

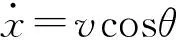
(1)

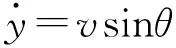
(2)

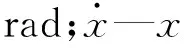
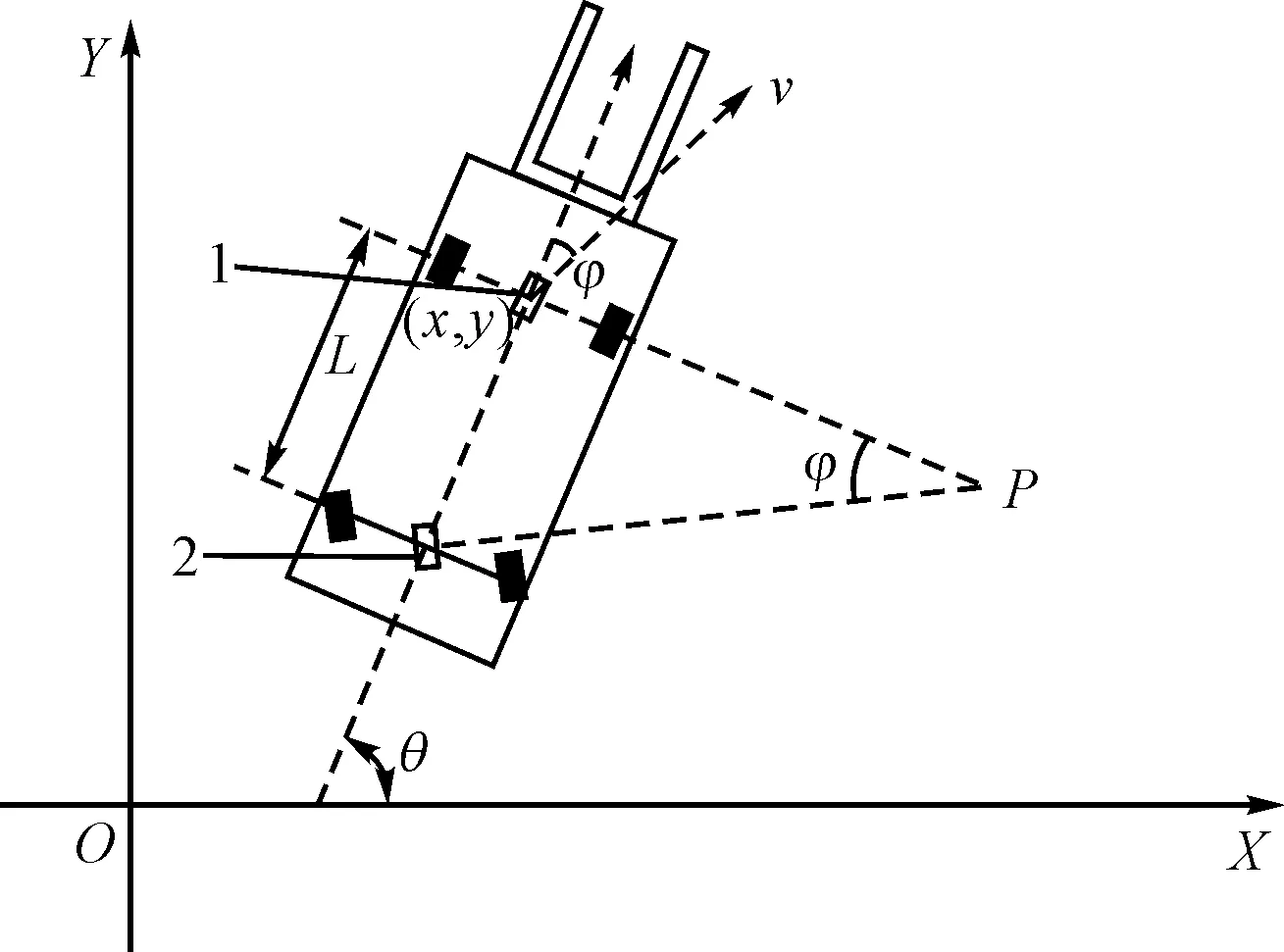
图3 智能转运叉车运动学模型1—等效驱动轮;2—等效转向轮

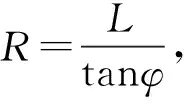
(3)

式中:L—叉车的轴距,m;φ—等效后轮转向偏角,rad;w—转向速度,rad/s;v—前轴中心速度,m/s。

智能叉车运动学模型为:

(4)

2.2 智能转运叉车参数约束

诺力FE4P20E型四支点前驱平衡重电动叉车基本参数如表1所示。

表1 叉车基本参数

智能叉车转向曲率为:

(5)

2.3 运动起终点约束

在登车前,调整位姿运动路径的起点及智能转运叉车的后轮转向角为零,航向角方向定义为X轴正方向,沿X轴方向左侧且垂直于X轴定义为Y轴正方向,起点定义为坐标系原点;登车桥尾板中点为调整位姿运动的终点,智能转运叉车在此处航向角应垂直于登车桥尾板,且后轮转向角为零。

此处叉车相对登车起点的相对位姿(Δx,Δy,Δθ),如图4所示。

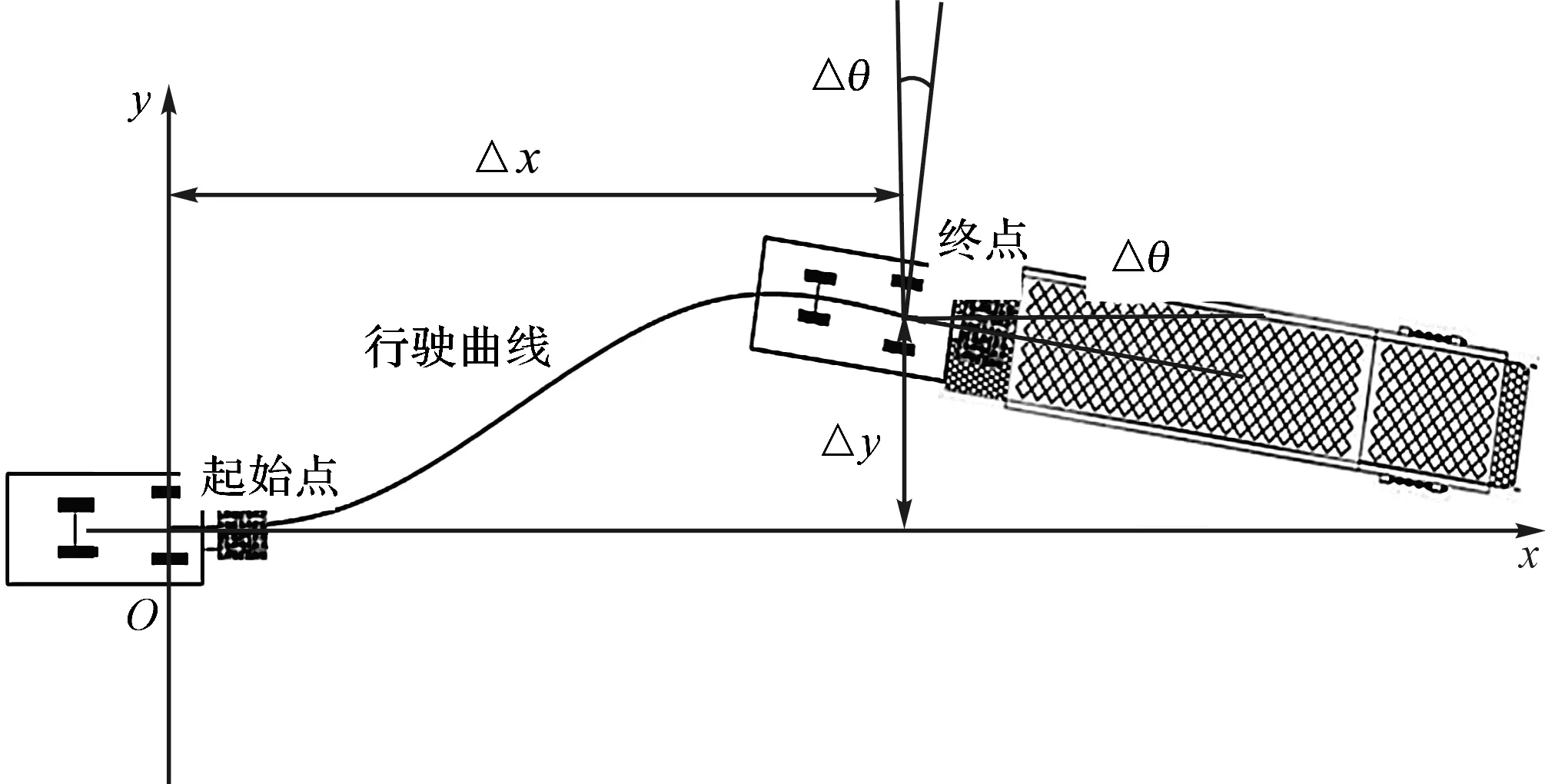
图4 登车运动起终点约束

图4中,Δx向右偏移为正;Δx向上偏移为正;Δθ以x轴逆时针偏移为正。

登车桥按类型分有移动式和固定式两种,按需求定制。

本文以某一普通移动式登车桥为例,该登车桥规格尺寸参数如表2所示。

表2 登车桥尺寸参数表

为避免发生翻车、碰撞登车桥等情况,通过登车桥的长度、宽度、翻板间隙、智能叉车前后轮距以及轮胎宽度的计算,可得叉车运动到终点位姿误差范围D≤230 mm,θ≤1.14°。

3 运动规划模型

3.1 运动规划的维度

在满足安全性和稳定性的要求,智能转运叉车运动规划中,在行走模块,叉车的运动输出动作主要由输入速度和转向角动作控制。虽然行走轨迹可以在二维平面上,但同时也要考虑时间维度,因此,行走轨迹就是一条在二维空间和一维时间中的三维曲线。

从动力学上来说,叉车有很大的惯性;从运动学上来说,叉车又属于非完整性系统,因此,只考虑当前位姿而没有前瞻性动作就无法准确跟踪规划行车路线。运动规划不仅包括路径规划,也考虑运动控制。这样由运动规划得出的一条在三维时空中的跟踪路径可以完整地描述智能叉车的运动全貌,并对该运动规划模型进行求解,从而实现对叉车的精确运动控制。

3.2 运动控制模型

为保持车身行驶平稳,避免急转向情况的出现,建立智能转运叉车运动规划模型,有必要考虑叉车运动的横向和纵向加速度、加加速度,即前进运动的速度、加速度和转向角的速度、加速度。

运动模型主要有恒速模型(CV)、恒加速度模型(CA)、恒角速度模型(CTR)和恒角加速度模型(CTRA)[16]。转向角速度对于高速行驶车辆影响较大,不同的运动模型轨迹会有较大的差别,因此,要在规划之初,根据叉车运动特性对运动模型进行合理决策。

为了简化智能转运叉车计算的复杂度,假设整个运动规划过程中车辆匀速行驶,给定行驶匀速度v=1.0 m·s-1,角速度w=π/6 s-1。由于加速转向减速转向时间较短可忽略不计,在该模型下简化为匀速转向阶段,且每个转向状态阶段持续时长相同。

CC曲线(continuous curvature path)是曲率线性变化的曲线,它由最小转弯半径曲线转换而来,对路径进行平滑化处理[17]。

本文研究了常见场景下的叉车运动规律,并在CC曲线的基础上进行了优化,提出了S型曲线的行车轨迹。此处按转向角状态转换将运动模型分为9个阶段,分别为:

(1)起始线型阶段。转向角为零且不变,车辆沿初始航向角直行;

(2)转向阶段。转向角匀速增加,车辆转向曲率增加;

(3)转向保持阶段。转向角保持不变,车辆沿固定半径圆弧行走;

(4)转向回正阶段。转向角匀速减小,车辆转向曲率逐渐减小;

(5)斜向直行阶段。转向角为零且不变,车辆沿当前航向角直行;

(6)反转向阶段。转向角反向匀速增加,车辆转向曲率增加;

(7)反转向保持阶段。转向角保持不变,车辆沿固定半径圆弧行走;

(8)反转向回正阶段。转向角匀速减小,车辆转向曲率逐渐减小;

(9)结尾直行阶段。转向角为零且不变,车辆沿当前航向角直行。

在运动模型的9个阶段中,每个阶段转向角状态持续时长用{T1,T2,T3,…,T9}表示,整个过程有10个时间节点,分别用{t0,t1,t2,…,t9}表示。其中：t0—开始时间;t9—结束时间。

定义第2阶段转向时左转为正,右转为负,转速为w,则第4阶段转速为-w,第6阶段转速为-w,第8阶段转速为w,且在这4个阶段转向过程持续的时间相同,则转向角表达式如下:

(6)

其中,第5阶段转向角φ5=w(t2-t1)-w(t4-t3)=wT2-wT4=0,第9阶段转向角φ9=-w(t6-t5)+w(t8-t7)=-wT6+wT8=0。

智能转运叉车的航向角为:

(7)

式中:L—叉车轴距。

X轴方向移动的距离为:

(8)

Y轴方向移动的距离为:

(9)

运动模型中转向角变换对应的θ、Sx、Sy变化曲线和行车轨迹如图5所示。

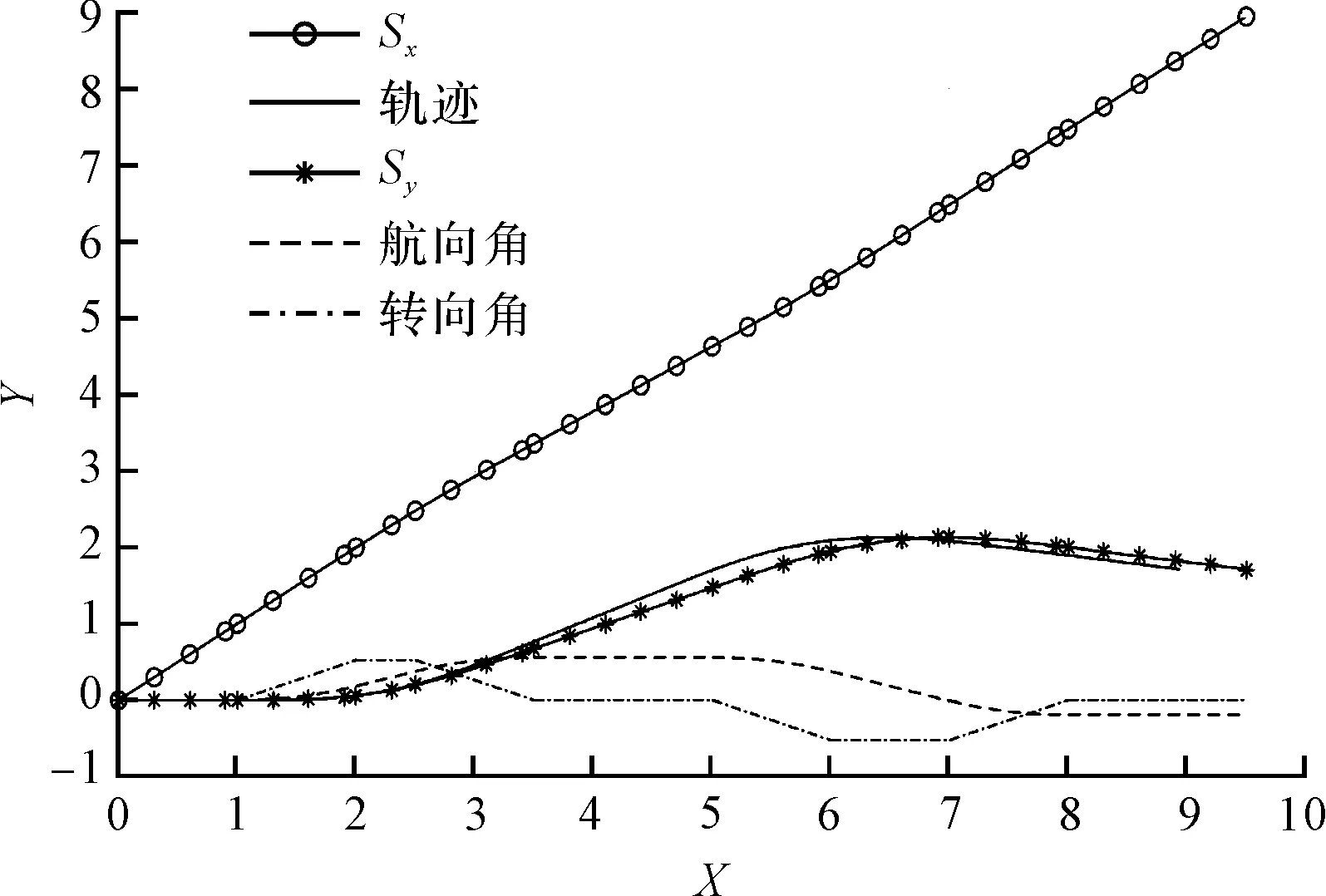
图5 转向角变换对应的θ、Sx、Sy变化曲线和行车轨迹

可见,在指定后轮转速和车速以后,通过控制每个阶段的时长即可控制叉车的最终位姿。

3.3 运动模型求解

运动模型规划要达到的目标是智能转运叉车从起点运动到终点时,满足以下3式:

(10)

(11)

(12)

在建立运动模型时,根据已知车速v,轴距L,转速w,设定第2、4、6、8阶段转向过程持续时间T2、T4、T6、T8相等,即T2=T4=T6=T8=Tφ,可知影响Δθ变化的有T3、T7,影响Δy变化的有T3、T5、T7、T9,影响Δx变化的有T1、T3、T5、T7、T9。

由此,先求解第3、7阶段持续时间T3、T7,其次求解第5、9阶段持续时间T5、T9,最后求解第1阶段持续时间T1。

3.3.1 T3、T7求解

根据式(10)可知,在其他7个阶段航向角变化之和为零。求解T3、T7时,已知φ3=wT2,φ7=-wT6;又T2=T4=Tφ,可得:

(13)

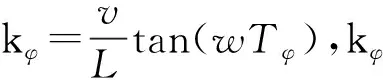
Δy、Δθ值分别为正、负时,T3与T7大小关系如图6所示。

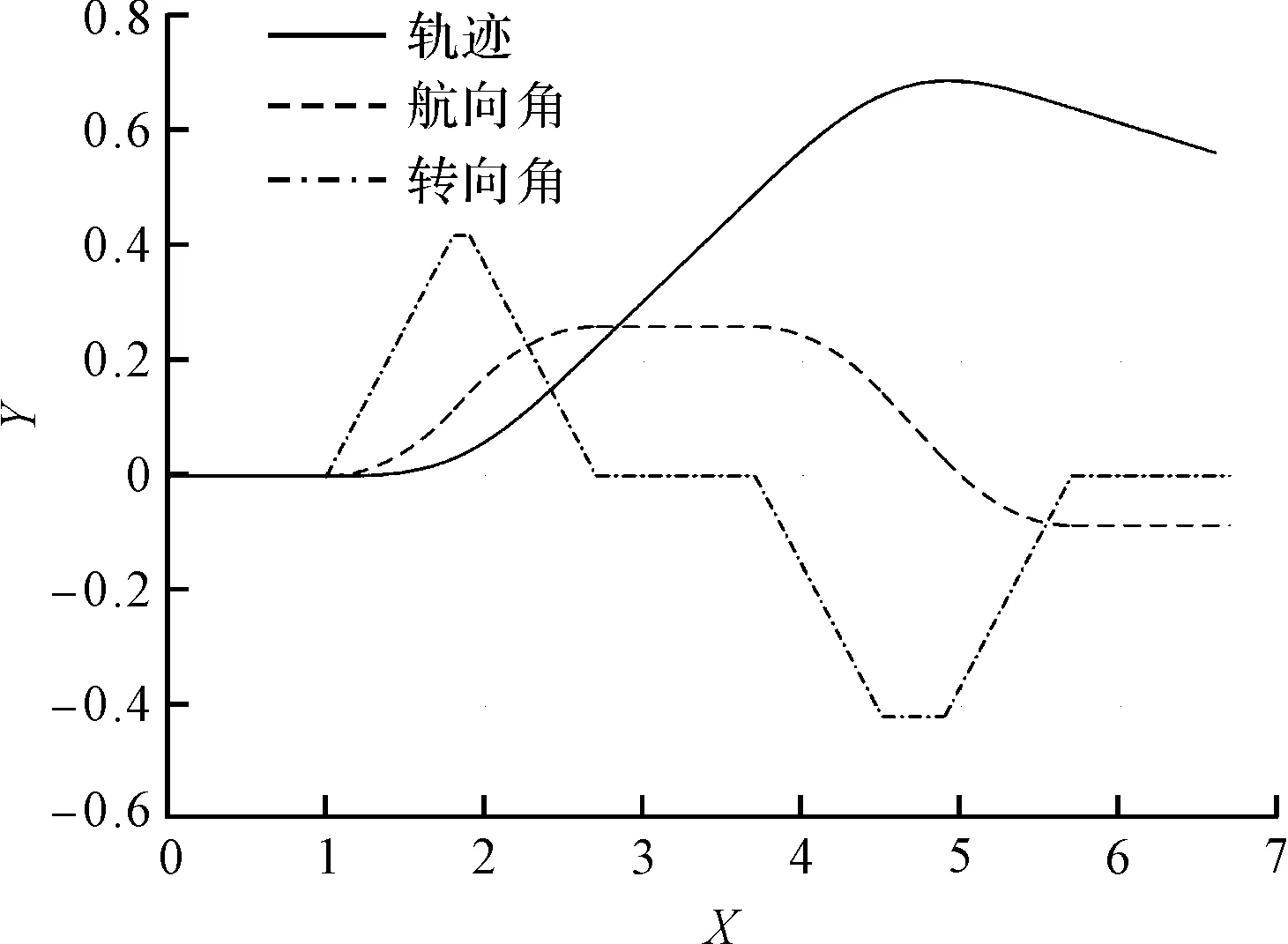
(a)Δy为正，Δθ为正时，转向角、航向角变化曲线及行车轨道

图6中:规定Δy向y轴正方向偏移为正,反之为负;Δy为正时,车辆先左转后右转,反之先右转后右转;

规定向x轴接近为正,远离x轴Δθ为负,可知Δθ为正时t3t7。

3.3.2T5、T9求解

求解运动规划模型中的T5、T9时,模型中的第2-4、6-8阶段的时长参数已由前文确定,当T5变化时,并不影响随后的第6-8阶段Δy6-8的变化值,举例如图7所示。

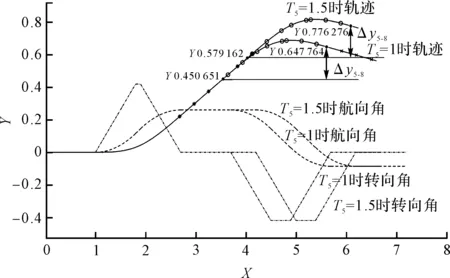
图7 其他参数不变,T5=1.0/1.5时Δy6-8的变化量对比

已知总的Y轴偏移量为Δy,且Δy1=0,根据前文得Δy2-4,6-8=Δy2+Δy3+Δy4+Δy6+Δy7+Δy8,则:

Δy5,9=Δy-Δy2-4,6-8

(14)

在运动模型中,第(5,9)阶段的行驶轨迹分别是两条不同斜率的直线,可知Δy5、Δy9是和时长t相关的一阶线性方程。

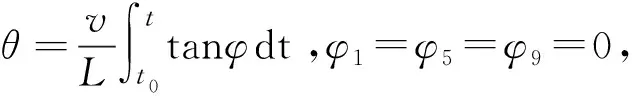
(15)

(16)

Δy5,9=ky5T5+ky9T9

(17)

式(17)中,T5和T9有多组解,调用MATLAB中的fmincon函数,以T5+T9取最小值为优化目标,建立方程组如下:

(18)

当Δθ为正时,ky5与ky9的值一个为正、一个为负,T5和T9总有解,且成正比。当Δθ为负时,ky5与ky9的值均为正值或负值,T5和T9的值成反比,若此时Δy5,9=|Δy|-|Δy2-4,6-8|<0就得出T5、T9为负值,与事实不符,要通过减小|Δy2-4,6-8|的值,即减小w或者Tφ的值来使T5和T9为正值。

等比例减小w或Tφ生成的轨迹如图8所示。

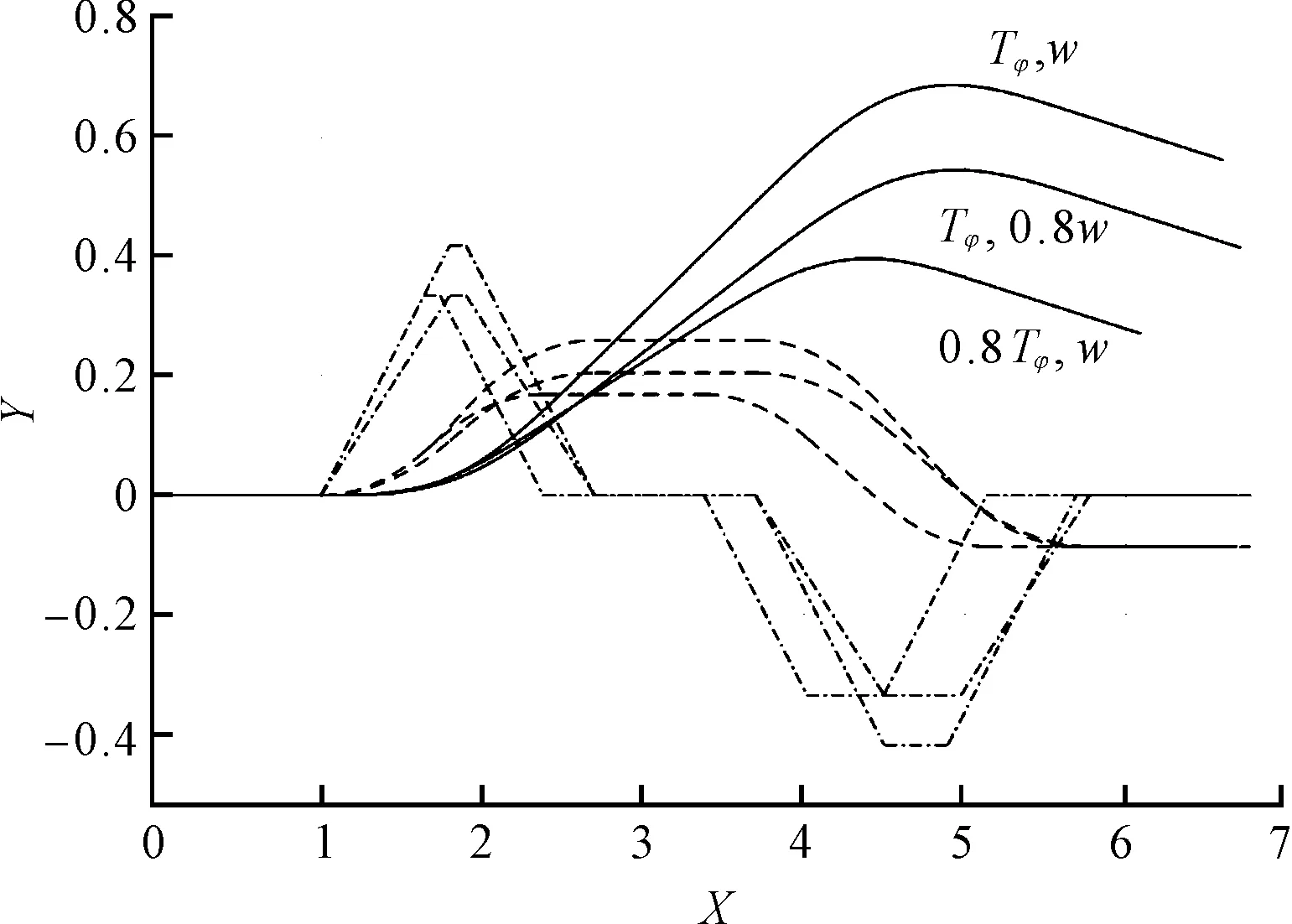
图8 等比例减小w或Tφ生成的轨迹

由图8可知:减小w对减小|Δy2-4,6-8|值的效果不如等比例减小Tφ,且会使X轴偏移量增大,对下一步求解T1不利,故选择通过减小Tφ减小|Δy2-4,6-8|值更合适。此处引入迭代法计算,直到T5、T9均为正解,但要注意tan(wTφ)值的变化会引起|T5-T9|值的变化,迭代时要重新计算T3、T7的值使Δθ保持不变。

3.3.3 T1求解

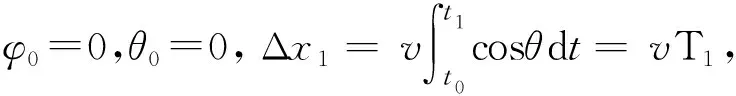
(19)

若Δx1=Δx-Δx2-9<0,则依旧用迭代法通过减小T5、T9或者Tφ的值,达到使Δx1>0的目的。

3.4 模型求解步骤总结

整个模型的求解过程用到了分步法、迭代法和fmincon函数。已知轴距L=1.5 m,目标Δx、Δy、Δθ,求解步骤总结如下:

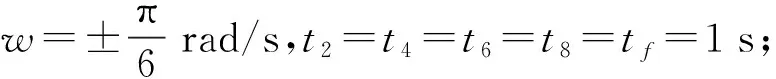
(2)根据Δy的正负,确定w的正负;

(3)根据Δθ的值,确定t7、t3的值;

(4)计算Δy2-4,6-8的值,并与Δy比较。若Δy-Δy2-4,6-8<0则减小w值,并重新计算Δy2-4,6-8的值;

(5)根据Δy-Δy2-4,6-8的值,确定t5、t9的值;

(6)计算Δx2-9的值,并与Δx比较。若Δx-Δx2-9<0则适当增大w的值,但要注意不能超出最大转向速度,然后再返回第3步;

(7)根据Δx-Δx2-9的值确定t1;

(8)代入所有控制参数,运行运动规划模型,生成行车轨迹,验证终点位置与航向是否在误差范围内。

4 仿真实例及分析

不同目标位姿(Δx,Δy,Δθ)下运动规划模型运算后生成的运动轨迹簇,如图9所示。

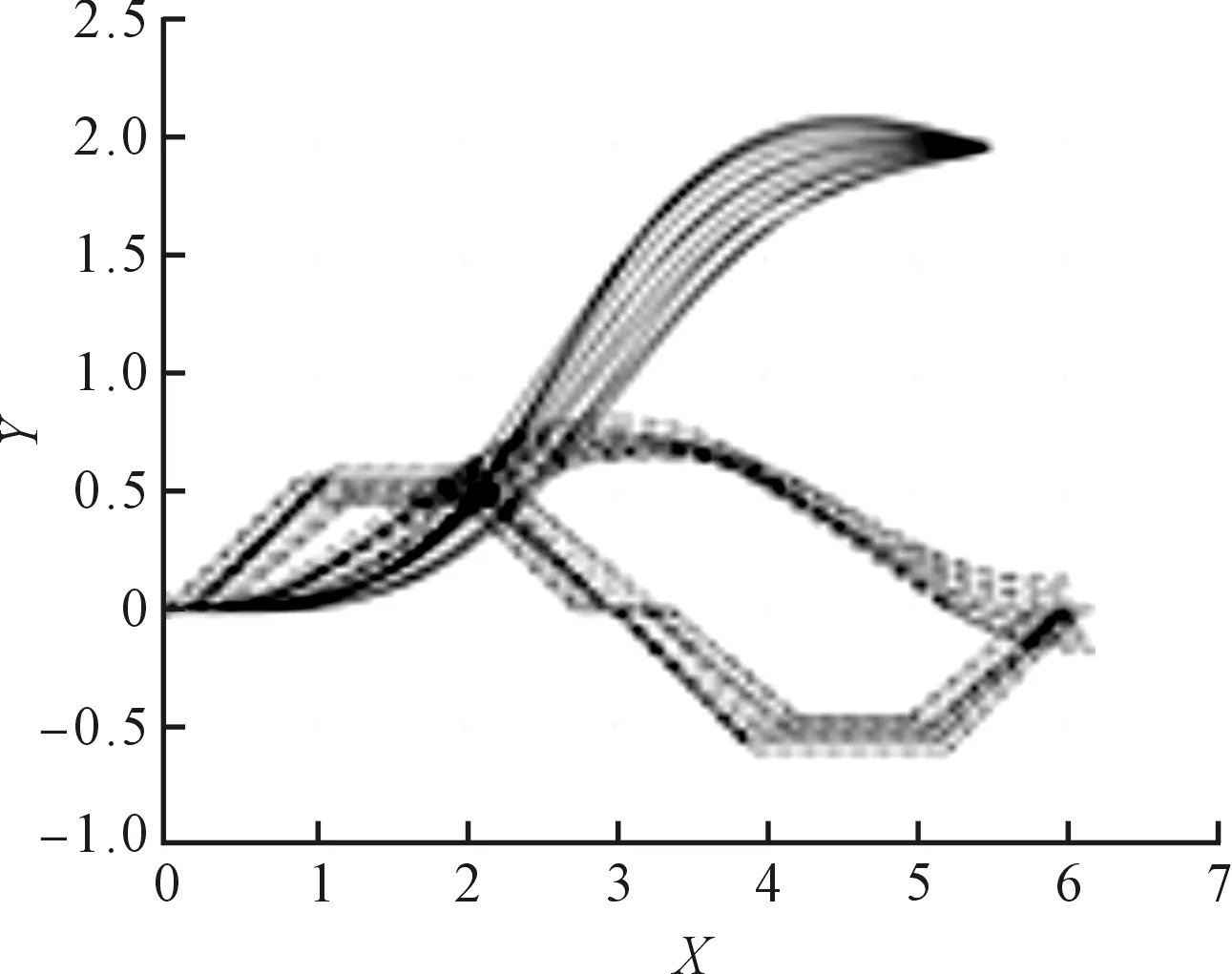
(a)Δx=5.5，Δy=2.0 (b) Δx =8.0，Δy =2.0 (c) Δx =8.0，Δy =1.0

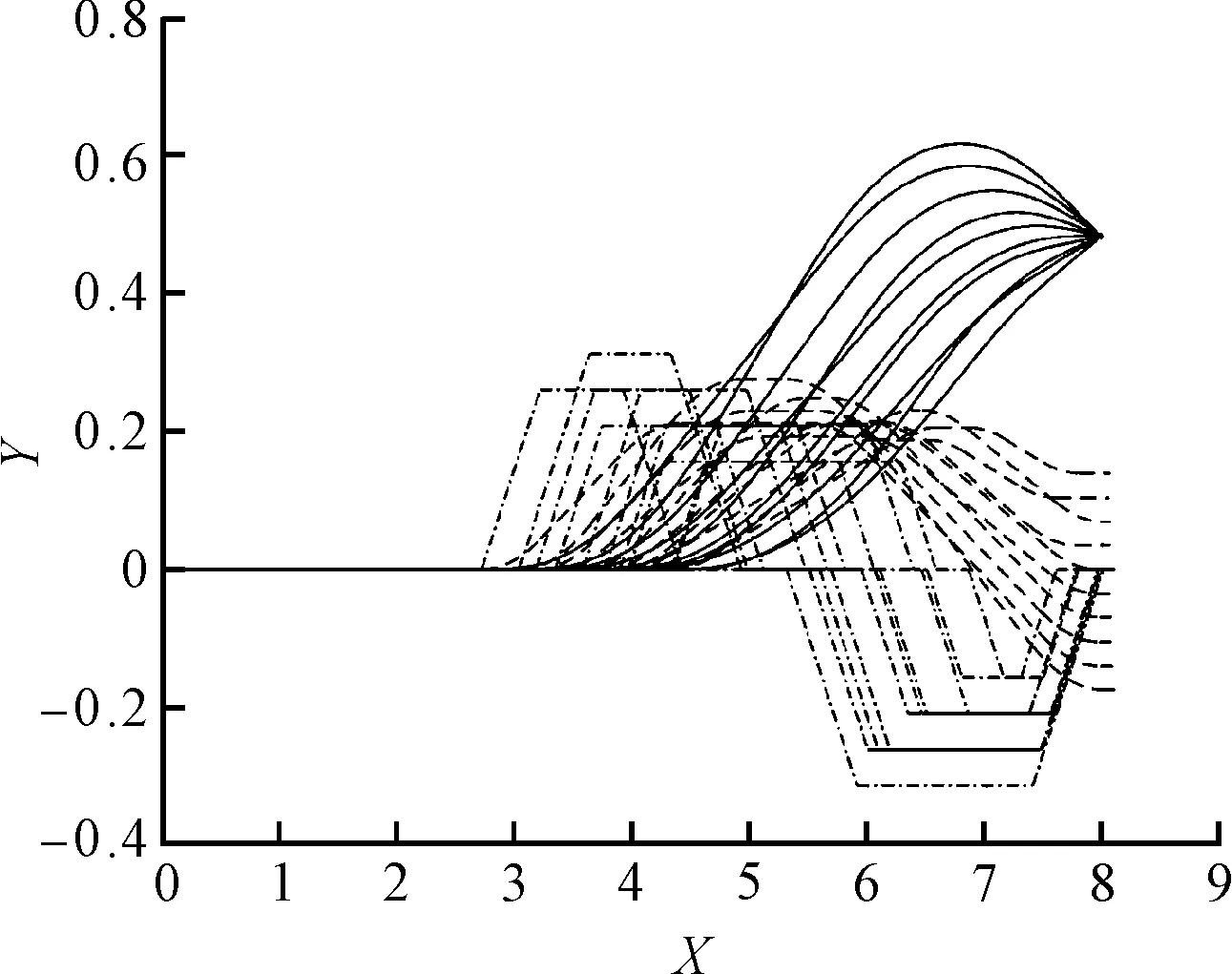
(d) Δx =8.0，Δy =0.5 (e) Δx =8.0，Δy =0.3 (f) Δx =8.0，Δy =-0.3

图9中,虚线是转向角变化曲线,点划线是航向角变化曲线,实线是叉车前轴中心行车轨迹。

对比图9(a～b)可知:在相同Δy值情况下,随着Δx值减小,w会有所增大,这是因为第一阶段时长只改变X方向距离;后面阶段完成求解而发生了后8个阶段在X轴偏移量超出了总的目标Δx值,为避免T1出现负值,通过调整w来重新求解运动模型。由此可见,在极限情况下(Δx最小,Δy最大),模型在范围内有解,即运动模型设计满足应用需求。

对比图9(b～d)中,Δx值不变,Δy值变化,可知随着Δy的减小,最大转向角wtφ在减小,即转向阶段在Y轴的偏移量超出了总的目标Δy值。为避免T3、T7出现负值,通过调整tφ来减小转向阶段的Δy值,使得模型有解,然后重新求解运动模型。

对比图9(b,i,c,h)可知,在Δx值相等、Δy值相反时,运动模型规划出的轨迹对称,即对w转向的控制很成功。

观察图9(d～g)生成的运动轨迹簇可知:Δθ<0时,随着Δy的减小,在Δθ为较大值时运动规划模型得不到行车轨迹;而Δy越小,模型无解时的最大Δθ值也越小。这时,需要调整策略,经过试验把tφ初始值调整为0.5 s时能得出最优运动规划结果。

调整转向策略的最佳范围如图10所示。

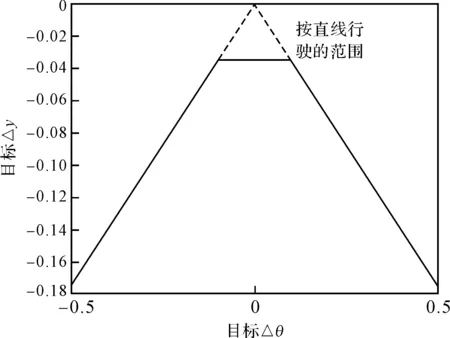
图10 调整转向策略的范围

图10中,对0<Δy<0.5且Δθ<0,调整为先右转;对0>Δy>-0.5且Δθ<0,调整为先左转。

调整转向策略后的运动模型求解出的运动轨迹如图11所示。

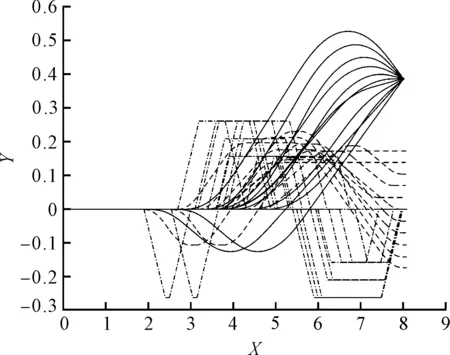
(a) Δy =0.4

对比图11(a～c)可知:在Δθ<0,Δy分别为0.4、0.3、0.2、0.1时,除Δy=0.1,Δθ=0.2外都能求出模型的解。在Δy值极小,且Δθ极小情况下,全程按直线行驶也满足误差范围,添加修正函数为:

(20)

(21)

融合未调整转向策略区域的模型算法,可以得到在目标位移和目标航向范围内的所有运动规划算法。至此,修正后的运动规划算法模型在全部情况下都有解,完成了适用于本文的智能转运叉车运动规划算法。

在计算效率上,在Intel(R)Xeon(R)CPU 3.50 GHz的计算机中,MATLAB2020b版本环境使用tic、toc函数生成多个控制点的B样条曲线轨迹,运行25次后得出平均运行时间为0.029 5 s。而本文的运动规划模型在100种不同目标中求解运行总时间为1.228 159 s,平均单一目标求解运行时间为0.012 3 s,效率比前者高59%。

5 结束语

在参考了普通叉车装车作业时运行轨迹特征,并结合叉车运动学分析的基础上,笔者建立了基于转向角变换的9种运行状态组成的叉车运动规划模型,并在MATLAB环境下对其进行了仿真验证。

研究结果表明:

(1)该运动规划算法模型能在前向位移5 m～8 m、侧向位移±2 m、航向角±10°范围内简单、准确、快速地生成满足多约束状态下的运动规划控制参数,平均运行时间约为0.012 3 s;

(2)模型改进了以往在固定场景下的路径规划算法,省去了需通过优化路径曲线光滑度来实现最优路径规划的过程,减少了叉车运行控制计算量,运行时间减少了约59%。

在今后的研究中,笔者将针对智能转运叉车目标位姿识别差错,或供叉车行驶空间过于狭窄的情况,进行叉车进退式运动规划研究,使叉车可以在更复杂的环境或场景内做二次运动规划。