基于响应面法的型钢混凝土闸墩损伤可靠度分析

吴 健，张小飞，陈 丹，肖天培，覃 培

(广西大学 土木建筑工程学院，南宁 530004)

闸墩是水利水电工程泄水建筑物的重要组成部分，传统的闸墩主要是采用钢筋混凝土结构，对大推力弧形闸门的闸墩而言，仅靠增加闸墩的厚度和配钢量来满足安全可靠的要求，显然不是最好的途径。型钢混凝土结构具有较大的刚性和良好的延性[1]以及承载能力高等优点，是一种比较理想的受力结构，将其应用于闸墩中承担较大的闸门推力、保证闸墩安全可靠运行是一种合理的选择。

型钢混凝土闸墩在运行过程中都避免不了会出现一定的损伤，目前对于型钢混凝土闸墩出现损伤后的安全可靠度研究较少，对型钢混凝土闸墩损伤可靠度还缺乏相应的评价。因此，开展存在损伤的型钢混凝土闸墩的可靠度研究是有必要的。本文利用刚度面积折减法对型钢混凝土闸墩进行损伤模拟，并利用响应面法拟合出闸墩的功能函数，结合JC法得出对称工况下损伤型钢混凝土闸墩的可靠指标，并通过灵敏度图研究型钢尺寸、型钢屈服强度和混凝土抗压强度和对型钢混凝土闸墩可靠指标的影响，为型钢混凝土闸墩的设计和运行管理提供参考。

1 基于响应面法的的可靠度分析

1.1 响应面概率设计方法

响应面概率设计是利用ANSYS中的概率设计模块里面的响应面法对结构进行可靠度分析。其原理是选用一个适当的、可以明确表达的响应面函数来近似代替无法明确表达的真实函数，即通过一些确定性的数值模拟和试验研究，并通过有限次的计算拟合出响应面，以代替未知的、真实的极限状态曲面。其方法主要是利用所建立的有限元模型，根据结构参数的不确定性来定义输入变量，利用输入变量的均值、标准差以及参数服从的分布类型，根据失效模式定义输出变量，进而利用ANSYS中概率设计模块自动进行抽样，再拟合得出所需的的输出变量。

响应面函数的形式主要包括线性响应面函数、二次响应面函数。其中，二次响应面函数分为含有交叉项或不含交叉项两种情况。目前主要采用的是二次响应面函数，因其形式简单且参数较少。考虑到精度和计算量问题，本文采用的是含有交叉项二次响应面函数形式。函数形式如下：

(1)

其中，a、bi、dij(i=1,2,…,n)表示公式中的待定系数。拟合的响应面示意图见图1。

图1 响应面示意图

二次多项式中的待定系数需要通过样本点来进行拟合求出，其中样本点一般是通过试验设计的方法选取。目前来说，样本点选取最常用的试验设计是采用二水平因子设计[2]或者中心复合设计[3]。为了保证拟合响应面的精度以及效率，本文采用中心复合设计。中心复合设计是最常用的实验设计方法，它是根据二次多项式的特点来构造的，所取的样本为各个因子的端点和设计空间的中心点，在二水平因子设计点的基础上，通过增加轴向点和中心点来完善响应面的模拟[4]，因此特别适应于二次多项式响应面[5]。利用ANSYS对结构进行可靠度分析时，其主要流程图见图2。

图2 ANSYS可靠度分析流程图

1.2 闸墩结构可靠指标的计算

利用响应面法计算结构可靠指标时，主要有以下方法：方法一是利用蒙特卡罗法在ANSYS得出的响应面上直接进行抽样，直接得到结构的失效概率，再由失效概率与可靠指标进行转换；方法二是在利用得出的响应面方程结合JC法进行计算，即用ANSYS所得出的响应面方程作为实际方程，然后再根据JC法对结构的可靠指标进行计算。JC法是通过当量正态化将结构中非正态的随机变量转化为正态分布的一种可靠指标计算方法。将结构中非正态的随机变量转化为正态分布，要求在设计验算点处，非正态分布的随机变量要与其等效的正态分布的随机变量的概率密度函数值和分布函数值相等[6]。即必须满足式(2)和式(3)：

(2)

(3)

式中：Fxi(•)、fxi(•)分别为非正态分布的随机变量Xi的分布函数以及分布密度函数；Φ(•)、φ(•)分别为标准正态分布随机变量Xi的分布函数以及分布密度函数；μxi、σxi分别为等效正态分布变量Xi的均值以及均方差。

所以利用式(2)和式(3)便可求出等效正态分布变量Xi的均值和均方差，分别为：

(4)

(5)

式中：Φ-1(•)为标准正态分布的分布函数的反函数。

直接在响应面上利用蒙特卡罗抽样得出的失效概率转化为可靠指标时，需要已知输出变量所服从的分布类型，才能进行失效概率与可靠指标的转化。但本文通过响应面法得出的输出变量并不确定其分布形式，而且直接在响应面上利用蒙特卡罗抽样并不能通过自动线性内插来修正中心展开点，计算结果精确度较差。因此，本文选取第二种方法即利用JC法对结构可靠指标进行计算。

2 建立型钢混凝土闸墩有限元模型

2.1 闸墩布置方式与模型参数选择

开敞式表孔的超泄能力大、结构简单、可靠度高，是水利水电工程最常用的泄水建筑物。如龙滩重力坝、溪洛渡拱坝、大藤峡枢纽、光照水电站、邕宁水利枢纽等一大批水利水电工程均采用了这种泄水建筑物形式，其工作闸门均采用弧形门，闸墩的结构形式基本相似。某水利工程的弧形门推力大小和闸墩厚度在已建和拟建的同类工程中，处于中等位置。为了研究具有代表性，本文以某水利工程中泄水闸坝为工程背景。

该工程采用开敞式表孔泄流，其单孔孔口的尺寸为22 m×14 m，溢流堰为宽顶堰，工作闸门采用弧形门，闸墩尺寸长41.6 m，高38.2 m，厚3.2 m，闸墩墩体以及堰体采用C30混凝土，牛腿支座处选取C40混凝土。根据《水工混凝土结构设计规范》(SL 191-2008)的相关公式，计算确定型钢的配钢量约800 cm2，取型钢尺寸为415 mm×363 mm×26 mm×26 mm。工程安全等级为Ⅱ级，破坏类型为二类。为了减少计算时间，在不影响计算分析结果的前提下，对工程中的闸墩进行了简化，不考虑检修门槽的影响。根据在工程中实际运行情况，为了便于研究本文仅考虑两侧弧形闸门均关闭的对称工况。闸墩所受的弧门推力荷载见表1。

表1 闸墩牛腿支座处在闸门关闭或开启时受力情况

2.2 闸墩有限元模型建立

在ANSYS中采用Solid65单元对混凝土进行模拟，选用随动强化模型(MISO)对混凝土单元进行分析，破坏准则为William-Wamke五参数破坏准则。根据文献[7]，型钢混凝土闸墩中布置的型钢选用Q345牌号H型钢，采用Beam188单元来模拟，其本构关系选用多线性随动强化模型(MKIN)。型钢的布置方式根据相关研究[7-11]，采用三型钢、保护层厚度为400 mm、长度为20 m、角度为25°的布置方式，并在闸墩两侧配置横、竖向构造钢筋，同时设有横向联接型钢。建模时堰体与地基之间看作是固接，考虑到两侧堰体的伸缩缝的存在，堰体两端不设置约束，不考虑型钢与混凝土之间的黏结滑移。有限元模型示意图见图3。

图3 有限元模型示意图

3 型钢混凝土闸墩的损伤可靠度分析

余天庆、楼志文[12-13]认为结构中的损伤使实际的结构材料既不均质也不连续，并且这种不均质不连续还将随变形过程不断演化。根据一些实际工程中闸墩的运行观测[14]，弧形闸门闸墩的裂缝主要集中在闸墩牛腿支座附近的范围内，而形成这些裂缝的主要原因是由于闸墩弧门支座处受到弧门水推力的作用，导致闸墩在支座处局部受到较大的拉应力，进而导致其混凝土开裂。

3.1 型钢混凝土闸墩损伤模拟

目前，结构损伤模拟方法一般是用来检验所提出的结构损伤的诊断方法。实际工程中，由于结构在运行过程中会产生一定的损伤，造成结构刚度降低，但对结构的质量几乎没有影响，闸墩在支座处局部受力开裂属于这类损伤。对这类损伤，目前采用数值模拟法主要是通过刚度折减法进行模拟。利用有限元数值模拟对型钢混凝土闸墩进行损伤模拟时，主要是通过减小结构单元刚度值来模拟各种损伤状况。减小单元的刚度值可以采用弹性模量折减法和面积折减法。弹性模量折减法主要是通过对单元的弹性模量进行折减，从而降低单元的刚度；面积折减法主要是通过减小结构的截面面积，降低单元的刚度。由于闸墩支座处的开裂主要是发生在表面的保护层混凝土，为方便研究，本文采用面积折减法来模拟表面混凝土的开裂损伤。为了确定损伤的模拟范围，本文先通过有限元法进行静力分析，在闸墩承受重力、静水压力及弧门推力荷载的情况下，确定闸墩支座处的裂缝分布范围，见图4。其中，红色代表第一批裂缝，较少的绿色代表第二批裂缝，还有少量的蓝色代表第三批裂缝。

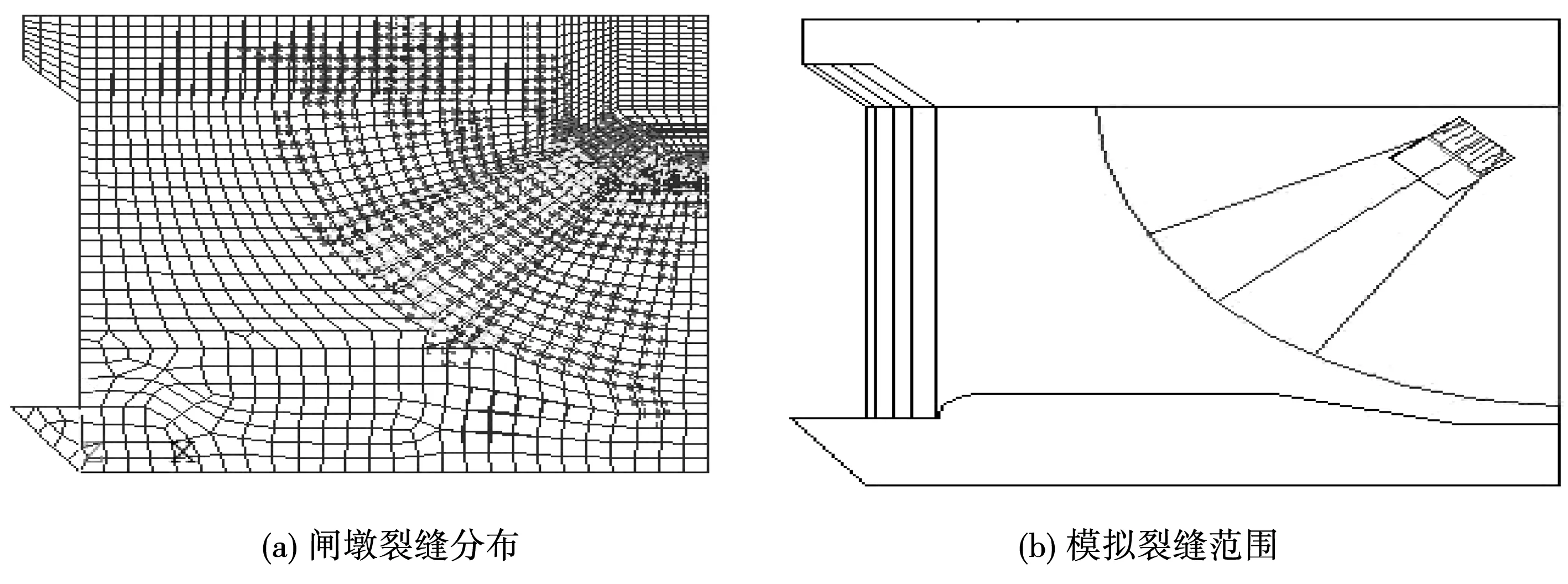
图4 型钢混凝土闸墩裂缝分布图

从图4中可以看出，其裂缝出现的范围较广且集中在牛腿附近的扇形受拉区域。本文通过面积折减法模拟裂缝，即折减裂缝范围内墩体厚度方向的混凝土面积，由于运行过程中结构裂缝损伤的程度难以测得，因此仅分析型钢混凝土闸墩在不同损伤程度情况下其可靠度变化。选取图4(b)中红色线段所包围部分的闸墩墩体混凝土截面面积作为混凝土裂缝范围，对其截面积分别折减混凝土保护层厚度10%和20%，研究结构不同损伤程度下的可靠度。

3.2 型钢混凝土闸墩输入参数

响应面方程中G、SFC、TFC、FFC、T和W分别是闸墩的输入参数，包括弧门均布荷载、型钢强度、墩体混凝土抗压强度、牛腿处混凝土抗压强度、型钢厚度、型钢宽度，其取值见表2。

表2 型钢混凝土闸墩统计参数

3.3 闸墩的目标可靠指标和承载力极限状态失效模式

根据《水工钢筋混凝土结构设计规范》(SL 191-2008)，本文闸墩的破坏类型为二类，安全等级为Ⅱ级，要求相应的承载能力极限状态的目标可靠指标为3.7。

对型钢混凝土闸墩而言，达到承载能力极限状态主要是承受弧门推力的支座附近的型钢发生屈服和闸墩开裂出现过大的变形。因此，本文主要是以型钢混凝土闸墩的型钢应力失效作为依据来判断型钢混凝土闸墩失效。以型钢的最大应力达到屈服应力作为失效判据，建立的型钢混凝土闸墩型钢应力失效的极限承载状态方程见式(6)：

Z=[σ]-σmax

(6)

其中：[σ]为型钢的屈服应力；σmax为型钢混凝土闸墩在荷载作用下其型钢最大的应力。

3.4 闸墩损伤可靠度分析

为了分析闸墩损伤程度对闸墩可靠度的影响，分别对型钢混凝土裂缝范围内的面积折减保护层厚度的0%、10%和20%。为保证所得结果有95%的准确性，计算时置信区间为0.95，得出型钢混凝土闸墩在此时的响应面方程分别见式(7)、式(8)和式(9)。

Z=0.847 4×SFC-248.320 5×G+2.827 1×108×W+(2.333 2×FFC-7.466 1×107)×(50.873 8×W-18.467 2)+2.849 6×108

(7)

Z=0.754 5×SFC-198.261 1×G+4.253 5×109×T+(3.606 3×10-8×SFC-13.349)×(40.901 3×G-7.853 0×107)+(0.272 5×SFC-1.008 9×108)×(2.885 5×10-7×FFC-9.233 6)+(2.885 5×10-7×FFC-9.233 6)×(38.897 2×G-7.468 2×107)+1.901 8×108

(8)

Z=1.017 1×SFC-248.375 9×G+5.229 6×109×T+3.843 9×108×W+(52.325 3×G-1.004 6×108)×(710.276 0×T-18.467 2)+(2.885 5×10-7×FFC-9.233 6)×(46.109 7×G-8.853 0×107)+5.462 0×107

(9)

根据响应面方程和表2统计参数的均值、标准差以及分布类型，利用JC法计算得出3个损伤情况下的闸墩可靠指标分别为β0%=4.74、β10%=4.30和β20%=3.75。可以看出，损伤程度越大，型钢极限承载能力状态目标可靠指标越小。当损伤折减保护层厚度达20%时，闸墩可靠指标略大于规范要求的3.7。

为了分析型钢混凝土闸墩型钢尺寸、型钢屈服强度、混凝土抗压强度对闸墩出现损伤时对可靠度的影响，本文通过在响应面方程上进行100 000次蒙特卡罗抽样得出其灵敏度图，见图5。从图5中可以看出，闸墩在损伤10%时，对承载能力极限状态可靠度敏感性较高的主要因素有弧门推力、型钢屈服强度以及型钢厚度；闸墩在损伤20%时，灵敏度图中敏感性较高的主要因素增加了牛腿混凝土抗压强度和型钢厚度。表明随着闸墩保护层损伤程度的增加，影响闸墩可靠度的因素会增加，闸墩可靠度对材料性能和数量的灵敏度提高，各参数的变化均对闸墩可靠度产生影响。

图5 对称工况损伤10%、20%灵敏度图

4 结 论

1) 型钢混凝土闸墩牛腿附近的扇形受拉区域表面保护层混凝土发生开裂损伤时，随损伤程度的加大，闸墩的可靠指标下降幅度增加，且下降速度有所加快。从无损至损伤10%时，下降的幅度为9.28%；损伤10%至损伤20%时，下降的幅度为12.79%。

2) 初步分析表明，型钢混凝土闸墩牛腿附近的扇形受拉区域表面保护层混凝土开裂损伤程度不超过20%时，闸墩的可靠指标还能满足规范要求；超过20%时即不能满足规范要求。因此，可以把型钢混凝土闸墩牛腿附近的扇形受拉区域表面保护层开裂损伤程度达20%作为型钢混凝土闸墩需要加固维修的参考依据。