考虑岩屑影响的大位移井机械延伸极限研究

郭骁 李思洋 周蒙恩 孟庆威 张菲菲

1.长江大学石油工程学院；2.川庆钻探工程有限公司长庆钻井总公司；3.大庆钻探工程公司地质录井一公司

大位移井的井眼轨迹在地层中水平延伸较长距离，可以增大油气层的裸露面积，大位移井眼连通多个储层，使得后期的储层改造和增产较为便利，增产效果明显。大位移井的应用减少了钻井的数量，节约了开发成本，提高了效益。但是在大位移井施工中，较多的大位移井下钻作业存在困难，所以对管柱的摩阻扭矩与大位移井极限延伸的研究是解决此类问题重要的一环。

钻柱力学方面，国内外学者先后建立了“软杆”和“刚杆”模型来研究管柱在井眼中的受力情况，并逐步加以改进。对于大位移井，岩屑堆积对井眼中摩阻扭矩的影响不可忽视。在延伸极限方面，高德利［1］提出了大位移井延伸极限的概念，闫铁［2］、付建红［3］、黄文君［4-5］等人对大位移井延伸极限做出修正与改进。本文利用井眼清洁与摩阻扭矩耦合模型做出大位移井机械极限延伸预测。

1 井眼清洁与摩阻扭矩耦合模型

图1 左表示环空中存在岩屑时的钻柱受力情况，其中wbpRdβ 表示钻柱单元体自重，wcRdβ表示钻杆单元体与井壁之间的接触力，µwcRdβ为摩擦阻力F和F+dF表示钻柱单元体两端的轴向力；岩屑床对钻柱受力的具体影响如图1 右所示，岩屑床对钻柱，受力的影响复杂且不可忽略，其中内部的力Fp、Frp、Fr、Fcw和Ffw表示岩屑床对钻杆不同方向的复杂相互作用。为了模拟岩屑对钻柱运动的确切影响，需要钻柱在整个井眼中的位置，通过复杂的有限元模拟才能获得。对于实际应用，假设一个简单的参数Fcb来表示岩屑床和钻柱之间的复杂相互作用，并通过实验数据与现场数据以数据驱动模型［6］来估算Fcb［7］。

图1 存在岩屑床影响的钻柱单元自由体及局部受力Fig.1 Free body and local stress of drill string unit under the influence of cuttings bed

为了考虑岩屑对井眼中扭矩和阻力的影响，通过修改软杆模型，提出了一种新的摩阻扭矩模型。将来自岩屑床的附加力添加到标准摩阻扭矩模型中，例如，对于下钻或滑动钻进的情况，将附加阻力Fcb加到钻柱的轴向，用来表示岩屑床对钻柱轴向力的影响。对于旋转钻进的钻柱，将阻力Fcb加至与钻柱曲线相切并与旋转方向相反的方向。该模型遵循传统软杆模型的假设，钻柱被看作一条软绳，忽略其抗弯强度，且钻杆与井眼轴线一致并与井壁连续接触。

将笛卡尔坐标系的单位向量i，j，k转化为弗莱纳坐标系的单位向量t，n，b，如图2。

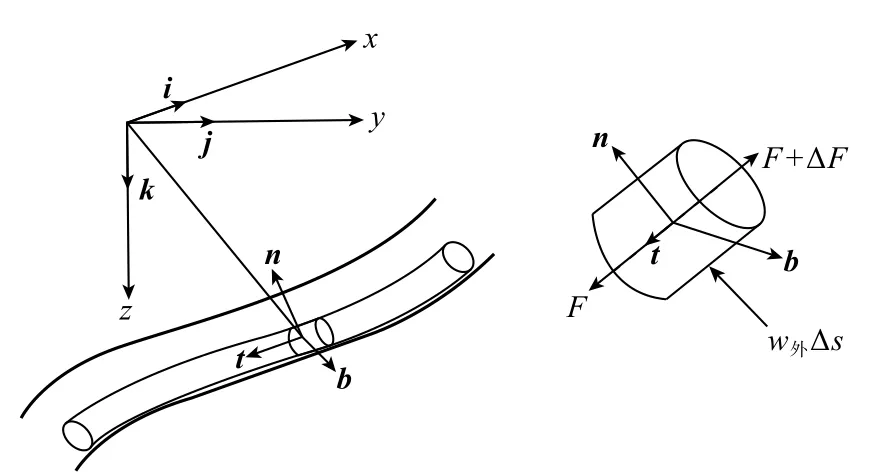
图2 三维井眼中钻柱微元自由体Fig.2 Free body of drill string infinitesimal in 3D hole

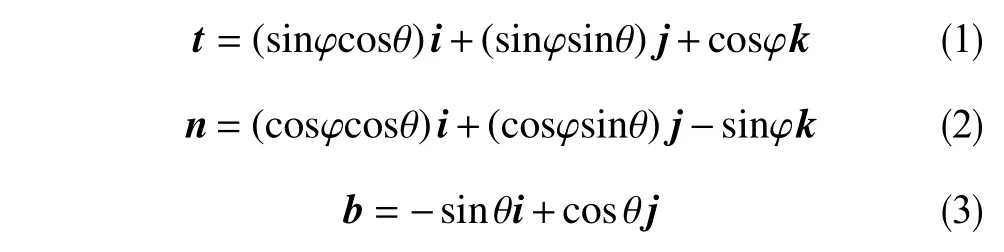
式中，φ为井斜角，°；θ为方位角，°。

通过对钻杆元件的自由体进行力学分析，单元体轴向力和扭矩平衡方程可以表示为

式中，Ft为轴向力，N；Mt为扭矩，N·m；wbp为钻柱的单位重量，kg；wc为接触力，N；tz、nz和bz分别为单位切向量、单位法向量和单位副法向量在z方向上的分量，无量纲；κ为井眼曲率，(°)/30 m；μ为摩阻系数，无量纲；α为n-b平面中接触力法向分量与n坐标轴之间的夹角，°；Fcb为岩屑床导致的附加力，N；rp为钻柱半径，mm。

通过解方程得单元体上的接触力和n-b平面中接触力法向分量与n坐标轴之间的夹角为

修正后的软杆模型的算法与标准摩阻扭矩模型相似，不同之处在于，在每个单元上，都需要基于局部钻屑床高度计算额外的阻力Fcb。从式(4)～(8)可以看出，Fcb等效于钻柱上的附加接触力。

在将井眼清洁模型与摩阻扭矩模型结合应用时，通过井眼清洁模型预测岩屑床在井眼中的整体分布。以井眼清洁模型预测的岩屑床分布作为输入进而改进软杆模型，计算出每个离散点的Fcb，最后得出钻杆上的摩阻与扭矩值。使用表1 的测试参数对模型进行摩阻实验，耦合模型的关键是通过研究一系列实验数据，得到Fcb和岩屑床高度的关系。

表1 测试参数Table 1 Test parameters

为了建立相关性，分别使用式(11)和(12)对岩屑床高度和岩屑床高度对扭矩的影响进行了归一化处理。

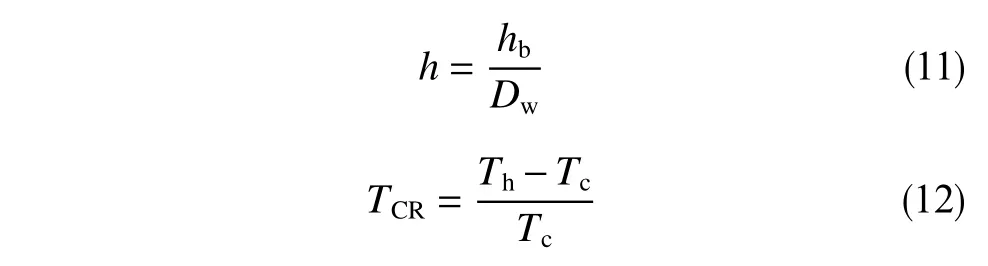
式中，hb为岩屑床高度，mm；Dw为井眼直径，mm；h为无量纲岩屑床高度；Th为岩屑床引起的扭矩变化，kN·m；Tc为无岩屑时的扭矩变化，kN·m；TCR表示岩屑床引起的扭矩变化率。

经过归一化处理后，无量纲岩屑床高度与扭矩变化率关系如图3 所示，可以发现二者大致呈指数形式。因此，在实验数据集的基础上建立了指数函数相关性，用式(13)表示。

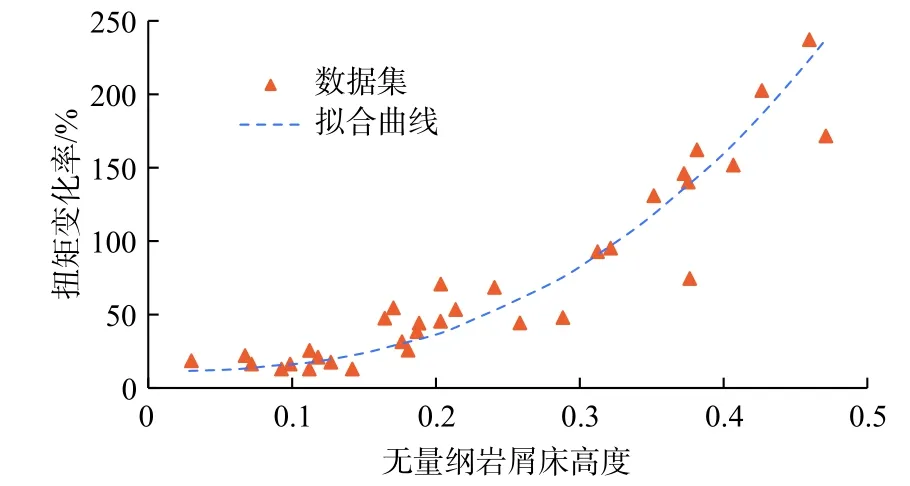
图3 无量纲岩屑床高度和扭矩变化率的关系图Fig.3 Relationship between dimensionless height of cuttings bed and torque variance ratio

其中，c=20，d=2.5。

因为实验是在模拟直井的设施上进行的，扭矩值与井眼和钻杆之间的接触力、井眼和钻杆之间的摩擦因数成正比。接触力在实验过程中保持不变，扭矩的变化只会导致摩擦因数的变化。因为参数是无量纲的，式(13)可转换为无量纲岩屑床高度与井眼和钻杆之间摩擦因数的关系

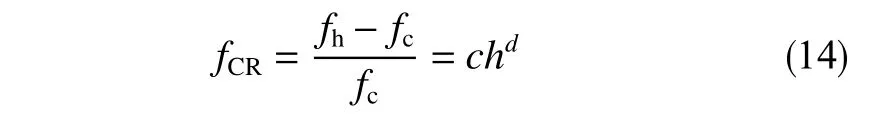
式中，fCR表示岩屑床引起的摩擦因数变化率；fh为无量纲岩屑床高度h下的摩擦因数；fc为相应井眼结构下无岩屑床时的摩擦因数。

在有岩屑的复杂井中进行扭矩计算，式(14)可以应用于具有给定局部岩屑床高度的摩阻扭矩模型中，岩屑床高度可从瞬态岩屑运移模型［8］得到。

与实验测试不同，在实际钻井中许多参数会发生变化。虽然由实验数据得出的相关性可能不适用于所有情况，但是摩擦因数和无量纲岩屑床高度的变化趋势是相同的。即，式(11)～(14)仍然有效，但c和d的值可能在不同的情况下有所不同。为了让模型的应用更加广阔，可以采用机器学习［9］的方法，根据历史钻井数据对模型进行训练后计算。

2 水平段机械延伸极限预测

大位移井水平段延伸极限是指在一定制约条件影响下，大位移井所能达到的极限长度。由于受到多种影响因素的制约，大位移井水平段不可能无限延伸，同时，根据相关研究，从经济角度来讲，水平段长度也不是越长越好。大位移井水平段延伸能力影响到钻探该类型井的施工效率以及全井成本，因此，对影响大位移井水平段延伸能力因素的分析，在大位移井钻井工程设计中是十分重要的。制约大位移井水平段机械延伸极限的因素主要有钻机性能约束、钻柱屈服约束和钻头运动约束［5］。

2.1 钻机性能约束

钻机的承载能力包括提升能力和扭矩输出能力。提升能力指在钻井作业中，起钻、下钻、钻进等工况下井口大钩载荷必须在钻机的额定载荷范围内；扭矩输出能力是指在钻柱旋转的工况下，井口扭矩不能超过钻机能够输出的最大扭矩。为保证钻机在水平段钻进过程中能够正常工作，需要准确预测不同工况下的井口大钩载荷和井口扭矩。

使用井眼清洁与摩阻扭矩耦合模型，考虑了岩屑对井眼中扭矩和阻力的影响，更加精准地模拟大位移井钻柱的真实受力。通过式(4)～(8)计算出井口的轴向力和扭矩。

2.2 钻柱屈服约束

根据井眼清洁与摩阻扭矩耦合模型计算出沿井深分布的轴向力和扭矩，然后计算出相应的轴向应力和切应力，根据第四强度理论计算钻柱微元上的等效应力 σ，为确保钻柱不发生屈服失效，钻柱等效应力应小于某值，其约束条件为

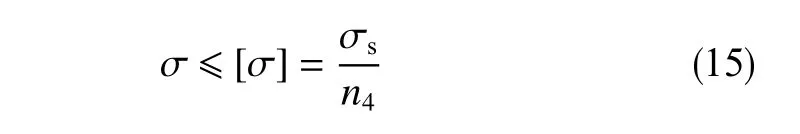
式中，σ为钻柱等效应力，Pa；[σ]为许用等效应力，P a；σs为钻柱的屈服强度，Pa；n4是为安全系数，无因次。

2.3 钻头运动约束

钻柱在滑动上提与旋转上提的过程中，有可能发生卡钻。在钻头处添加一个上提阻力来进行卡钻情况模拟。所以钻头位置的轴向力与扭矩必须等于模拟卡钻阻力与扭矩，而且钻头处钻压与扭矩必须大于岩石的门限钻压与门限扭矩。

3 实例分析

3.1 实例井简况

某井是一口水垂比大于5 的大位移井，井身结构为四开井，如图4 所示，井眼轨迹数据如表2 所示。该井平台井架提升能力为3 629.75 kN，顶驱提升能力为7 352.91 kN，顶驱最大连续输出扭矩为88.81 kN·m，旋转速度为100 r/min。

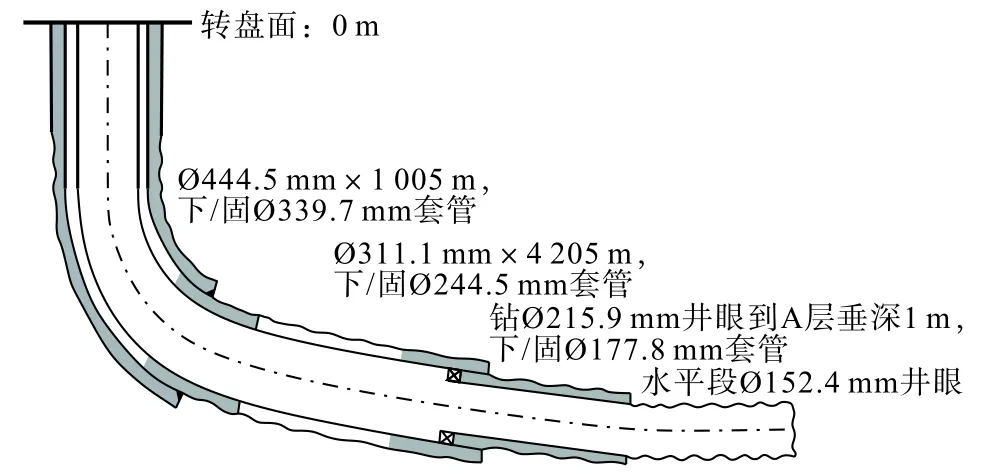
图4 井身结构Fig.4 Casing program

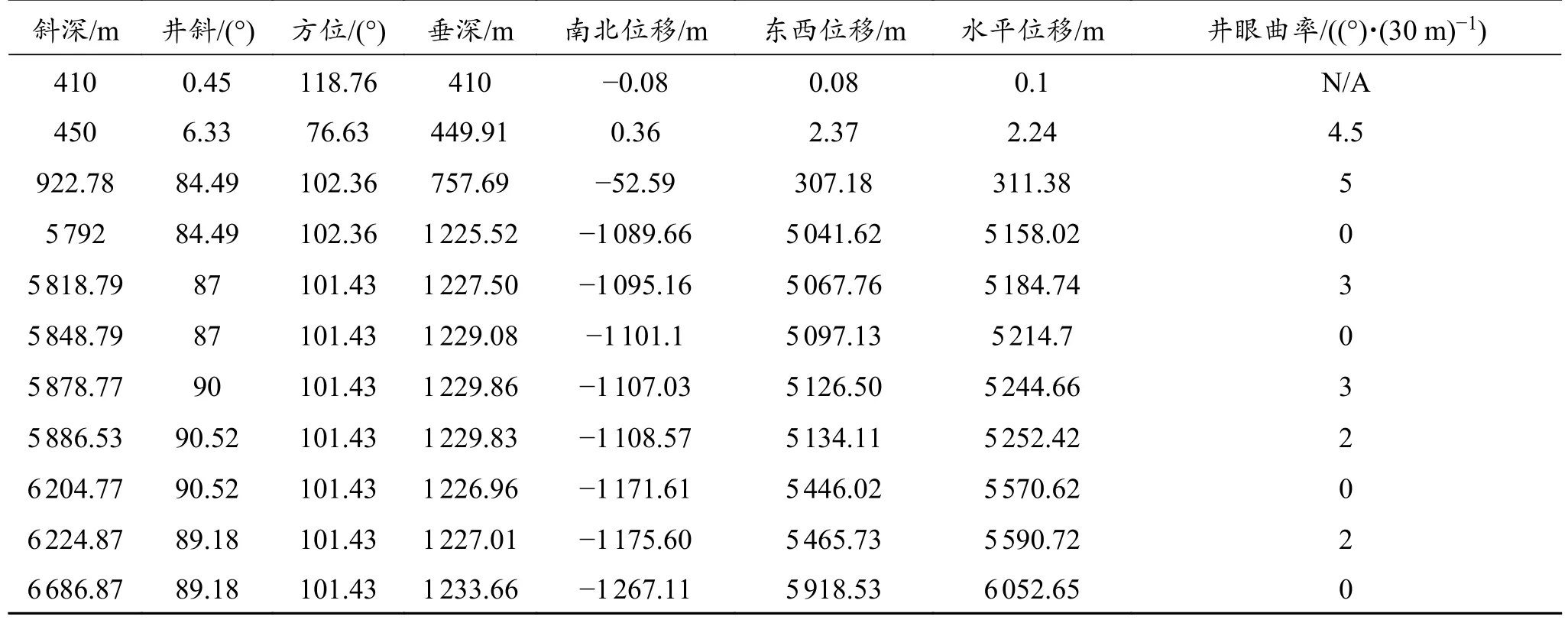
表2 井眼轨迹数据Table 2 Data of well trajectory

3.2 摩阻扭矩

摩阻扭矩计算参数如下：裸眼摩阻系数0.3，套管摩阻系数0.25，钻井液密度1.03 g/cm3，钻具活动速度0.3 m/s，旋转速度100 r/min，钻进钻压44 kN，钻头扭矩2 711 N·m。假定水平段岩屑床高度是40 mm 和80 mm，使用井眼清洁与摩阻扭矩耦合模型计算不同工况下有效轴向力与扭矩分布。

图5 为使用耦合模型分别计算水平段岩屑床高度40 mm 和80 mm 不同工况下的钻柱有效轴向力分布，结果表明，起钻工况下，钻柱受拉影响最大，但在岩屑床高度40 mm 的情况下未达到钻柱拉力极限，当岩屑床高度提升至80 mm 时，钻柱在起钻工况下达到拉力极限，发生断裂；下钻及滑动钻进工况下，钻柱受压，在岩屑床高度80 mm 情况下，钻柱在井口～400 m 时达到螺旋屈曲临界值，发生螺旋屈曲，轴向压力陡增。图6 为使用耦合模型分别计算岩屑床高度40 mm 和80 mm 不同工况下的钻柱扭矩分布，结果表明，在岩屑床高度80 mm 时，旋转钻进与倒划眼均达到扭矩极限，且在旋转钻进工况下，钻柱在井口～993 m 达到扭矩极限。

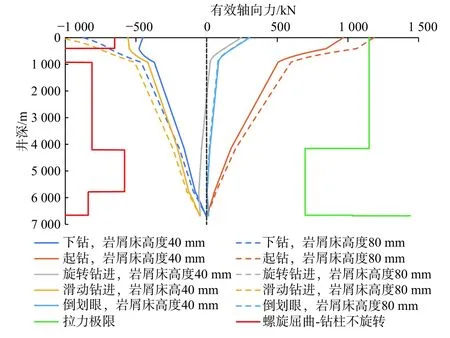
图5 不同工况下有效轴向力随钻柱分布Fig.5 Distribution of effective axial force along drill string under different working conditions

图6 不同工况下扭矩随钻柱分布Fig.6 Distribution of torque along drill string under different working conditions

如图7 所示，在滑动上提工况下，随着岩屑床的堆积，即岩屑床高度的提高，钩载随井深增大。如图8 所示，在滑动钻进工况下，随着岩屑床高度的提高，钩载随井深减小，但当井深增加到一定深度后，钩载迅速减小，造成此现象的原因是钻柱发生屈曲产生的高摩擦阻力，当钩载为0 时的井深为延伸极限。通过对比分析，滑动钻进是滑动工况下更为限制延伸极限的工况，以岩屑床高度为40 mm 为标准计算，机械延伸极限为6 156 m。

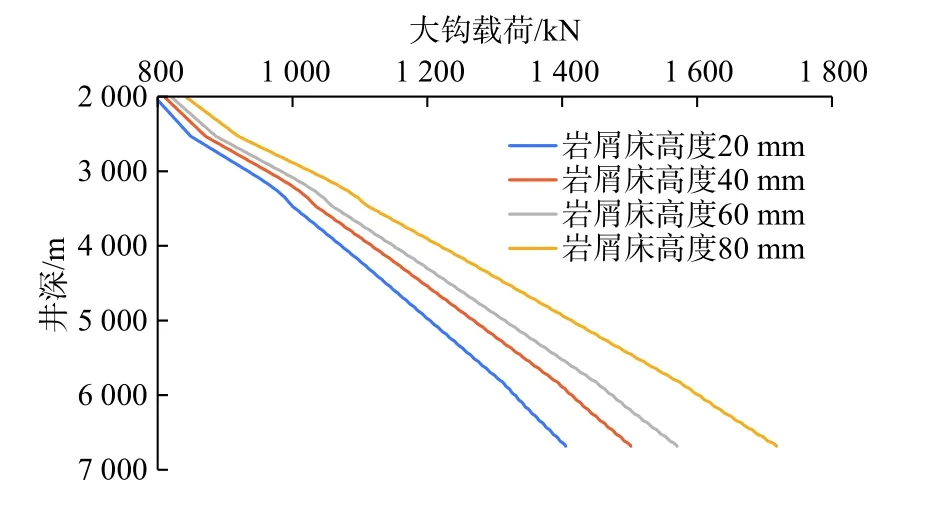
图7 滑动上提大钩载荷与井深关系Fig.7 Relationship between hook load and well depth during slide lifting

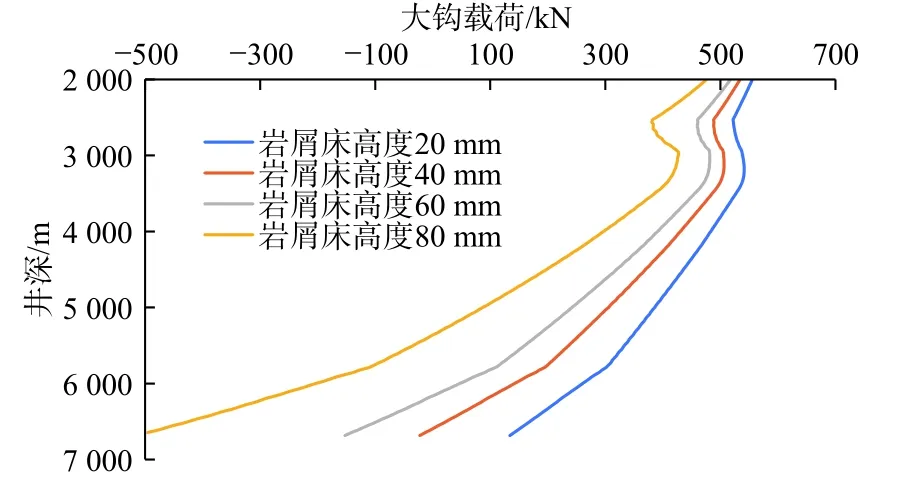
图8 滑动钻进大钩载荷与井深关系Fig.8 Relationship between hook load and well depth during slide drilling

如图9 所示，在旋转上提工况下，随着岩屑床的堆积，即岩屑床高度的提高，井口扭矩随井深增大。如图10 所示，在旋转钻进工况下，随着岩屑床高度的提高，井口扭矩随井深增大，当井口扭矩达到额定扭矩时的井深为延伸极限。通过对比分析，旋转钻进是旋转工况下更为限制延伸极限的工况，以岩屑床为40 mm 为标准计算，机械延伸极限为9 035 m。

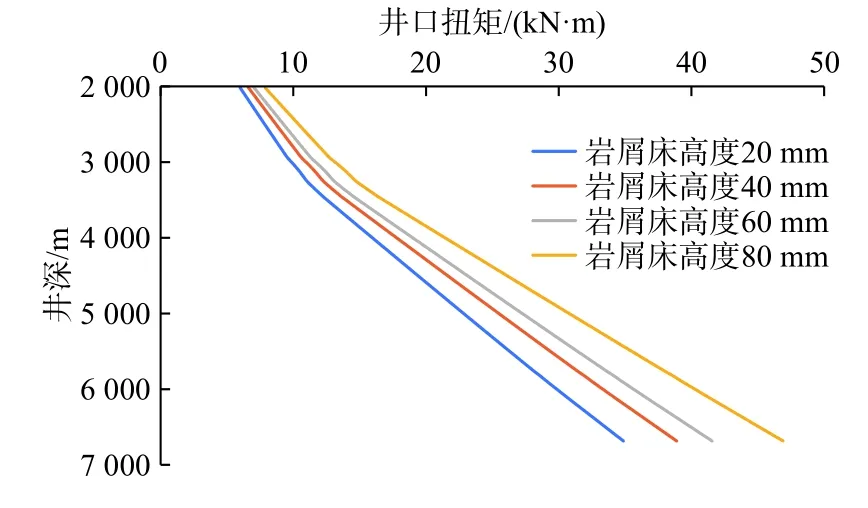
图9 旋转上提井口扭矩与井深关系Fig.9 Relationship between wellhead torque and well depth during rotary lifting

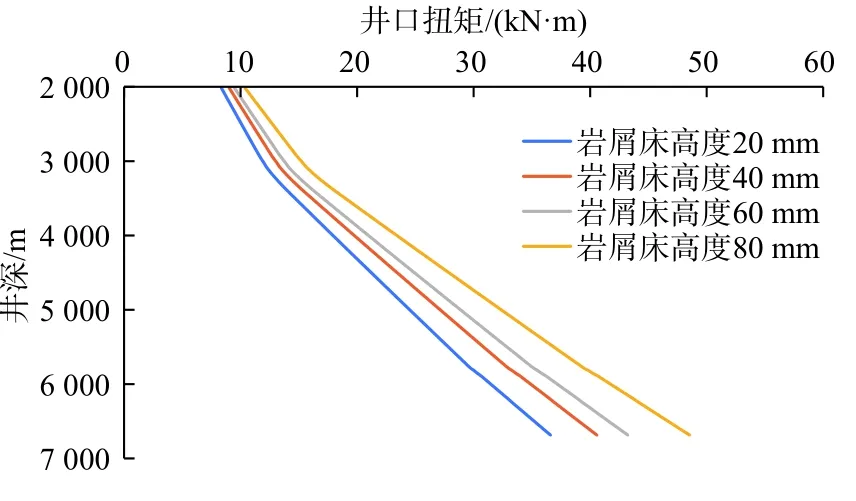
图10 旋转钻进井口扭矩与井深关系Fig.10 Relationship between wellhead torque and well depth during rotary drilling

3.3 大位移井机械延伸极限预测

对于滑动工况来说，机械延伸极限指起钻和滑动钻进延伸极限的最小值；对于旋转工况来说，机械延伸极限指倒划眼和旋转钻进延伸极限的最小值。

在相同钻机性能、仅改变岩屑床高度的情况下，使用上述钻进参数计算不同钻进方式的机械延伸极限，如图11 所示。结果表明，随着岩屑床高度的增加，机械延伸极限相应降低，而且随着岩屑堆积到一定程度后，对延伸极限的影响显著。岩屑床高度的增加对不同钻进方式的机械延伸极限的变化趋势相同，但滑动钻进的延伸极限明显低于旋转钻进。

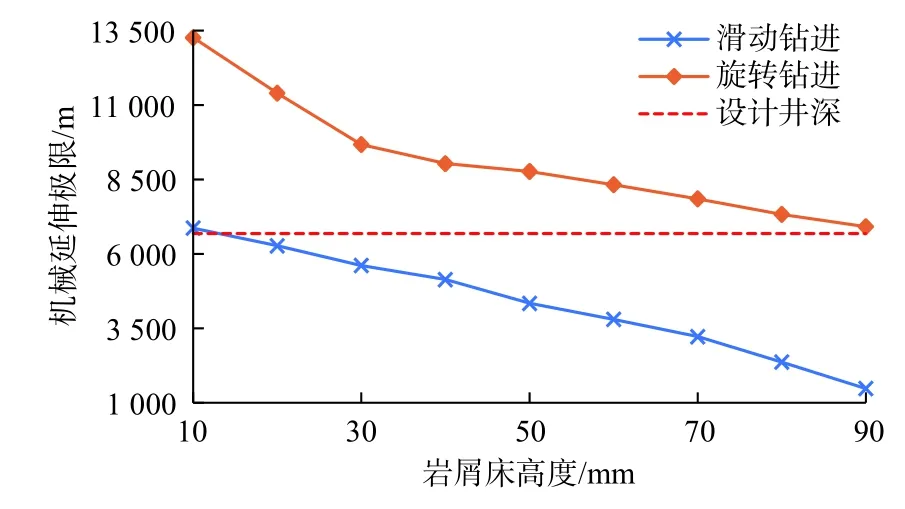
图11 不同岩屑床高度对机械延伸极限的影响Fig.11 Influence of the height of cuttings bed on the mechanical extension limit

4 结论

(1)考虑岩屑床对井筒中摩阻扭矩的影响，通过对前人的软杆模型进行修正，建立井眼清洁与摩阻扭矩耦合模型。提出大位移井水平段机械延伸极限的约束条件，并建立预测模型。

(2)使用井眼清洁与摩阻扭矩耦合模型进行实钻井摩阻扭矩分析，分别计算水平段岩屑床高度40 mm 和80 mm 下钻柱有效轴向力和扭矩分布，校核钻柱强度。岩屑堆积到一定程度后，钻柱屈服约束制约大位移井机械延伸极限；计算不同水平段岩屑床高度与不同工况下大钩载荷与井口扭矩，岩屑堆积对钩载与井口扭矩影响显著；分析不同岩屑床高度对机械延伸极限的影响，在无法提升钻机性能情况下，提高井眼清洁效率可有效提高延伸极限。

(3)井眼清洁与摩阻扭矩耦合模型仍需要根据历史钻井数据通过机器学习进行训练；大位移井延伸极限也受到钻井水力学［10］的限制，而且井眼清洁会缓解岩屑堆积。本文仅讨论岩屑床对机械延伸极限的影响，实际使用应综合分析。