不同卫星遥感降水产品在辽东山区的适用性及修正方法研究

裴立山

(辽宁江河水利水电工程建设监理有限公司，沈阳 110003)

0 前 言

随着卫星降水遥感产品的不断被应用到水利各个领域，不同产品的适用性也逐步得到相关研究[1]。其中CMA和JMA两种卫星遥感降雨产品被应用较为广泛[2-8]。但由于不同卫星遥感降水产品的时效性等原因，在不同区域有其适用性的问题[9]。需要结合区域实测降水对不同卫星遥感降水产品进行适用性的分析，从而分析出适合于降水特点的卫星遥感降水产品[10]。此外卫星遥感降水产品需要结合实测降水量，进行修正后才能提高其和实测降水量的吻合度[11]。近些年来对于卫星遥感降水产品修正方法取得一定研究成果[12]，这其中卡尔曼滤波模型对卫星遥感降水产品修正具有较好的效果，但在辽东山区还未得到相关研究。辽东山区属于辽宁省暴雨易发区，亟需要增加卫星遥感降水产品数据作为区域面降水量分析的重要补充。为此文章结合当前应用两种较为成熟的卫星遥感降水产品数据，分析其在辽东山区的适用性，并结合卡尔曼滤波模型对其雨量修正进行精度的探讨。研究成果对于卫星遥感降水产品在辽东山区的应用具有重要参考价值。

1 降水量修正方法

卫星遥感降水产品主要采用卡尔曼滤波模型进行修正，模型降雨量修正方程为：

x(t)=a1(t)x(t-1)+a2x(t-2)+a3(t)x(t-3)

(1)

式中：x(t-1)、x(t-2)、x(t-3)分别为不同时刻的降水产品数据，mm；a1、a2、a3为模型修正参数；x(t)为不同时刻下降雨修正量，mm。(t-1)为时刻对应的降雨量修正方程为：

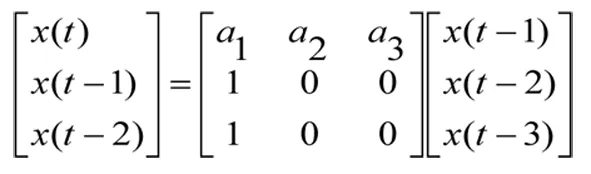
(2)

模型对各变量初始值采用人工神经网络方法进行转换：

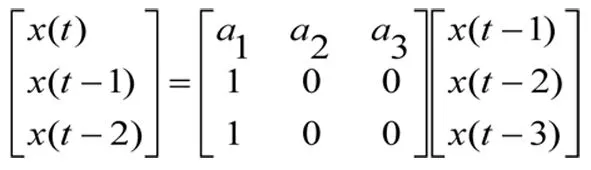
(3)

在变量初始值转换的基础上对其变量进行修正：

x(t)=Φ(t)x(t-1)w(t)

(4)

式中：Φ(t)为模型转移矩阵；w(t)为变量修正权重，对模型变量进行标准化计算：

x(t)=Φ(t)x(t-1)+Γw(t)

(5)

在标准化的基础上对卫星降水产品进行同化修正计算：

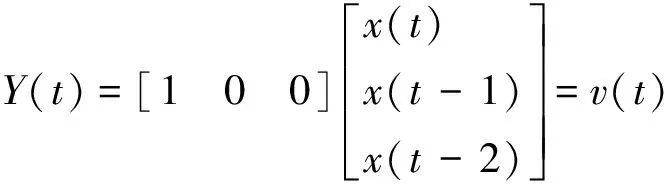
(6)

对其模型变量进行矢量化计算：

Y(t)=HX(t)+v(t)

(7)

式中：v(t)为实测降水数据系列；H=[1，0，0]为模型修正矩阵。模型对不同时刻变量权重进行计算：

(8)

式中：w(n0)、w(n0+1)为不同实测降水数据系列修正权重值；η为计算时段，h；P为降水数据系列个数；ξ为修正误差，%。模型采用动量权重系对模型收敛度进行转换：

(9)

对降雨产品修正误差进行计算：

(10)

式中：m为修正降雨量序列数目；k为修正降水量，mm；y为气象观测降水量，mm。

2 实例应用

2.1 研究区降雨特点

文章以辽东山区为研究区域，区域位于辽宁省暴雨中心区，夏季降水量占年降水量的比重高于50%，多年平均降水量约为800-1000mm。降雨时空分布差异性较大，空间分布总体呈现南大北小的变化分布。文章结合辽东山区降水实测数据，对比分析CMA和JMA两种卫星遥感降雨产品在区域降雨分析的适用性，并结合卡尔曼滤波模型对卫星遥感降水产品进行修正。

2.2 适用性分析

结合气象降水数据，对CMA和JMA两种卫星遥感降雨产品在不同时段以及雨量级别下的降雨误差进行统计分析，未来6h不同降雨等级条件下的CMA卫星降雨与实测降雨的误差统计结果，见表1；未来6h不同降雨等级条件下的JMA卫星降雨与实测降雨的误差统计结果，见表2。

从两种卫星遥感降水产品数据分析可看出，CMA和JMA两种卫星遥感降雨产品在辽东山区中雨量级别下的误差要好于大雨及大雨以上雨量误差，这主要是因为大雨等级下影响因素要高于中雨以及小雨量级，因此其误差相对较高。从误差统计检验结果可看出，两种卫星遥感降雨产品的误差统计特征值均可满足90%的误差检验要求，表明两种卫星遥感降水产品在辽东山区均具有一定的适用性，但CMA降雨产品的误差统计检验效果总体好于JMA卫星遥感降水产品的误差统计检验效果。

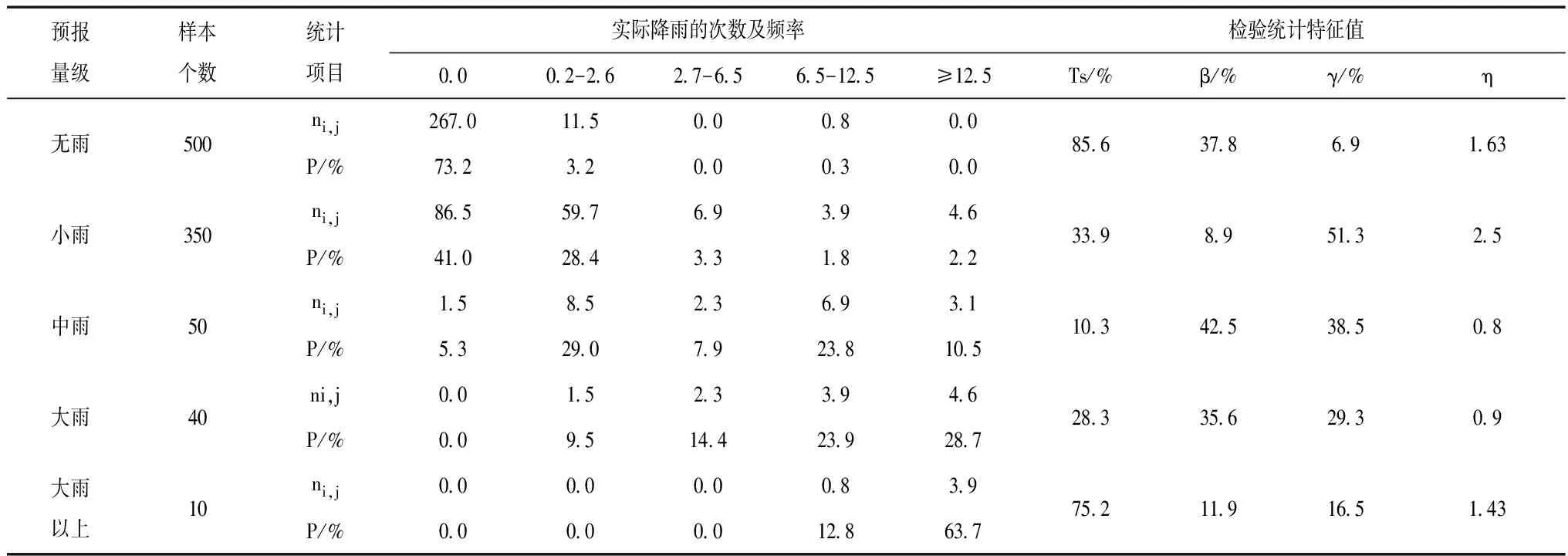
表1 未来6h不同降雨等级条件下的CMA卫星降雨与实测降雨的误差统计结果

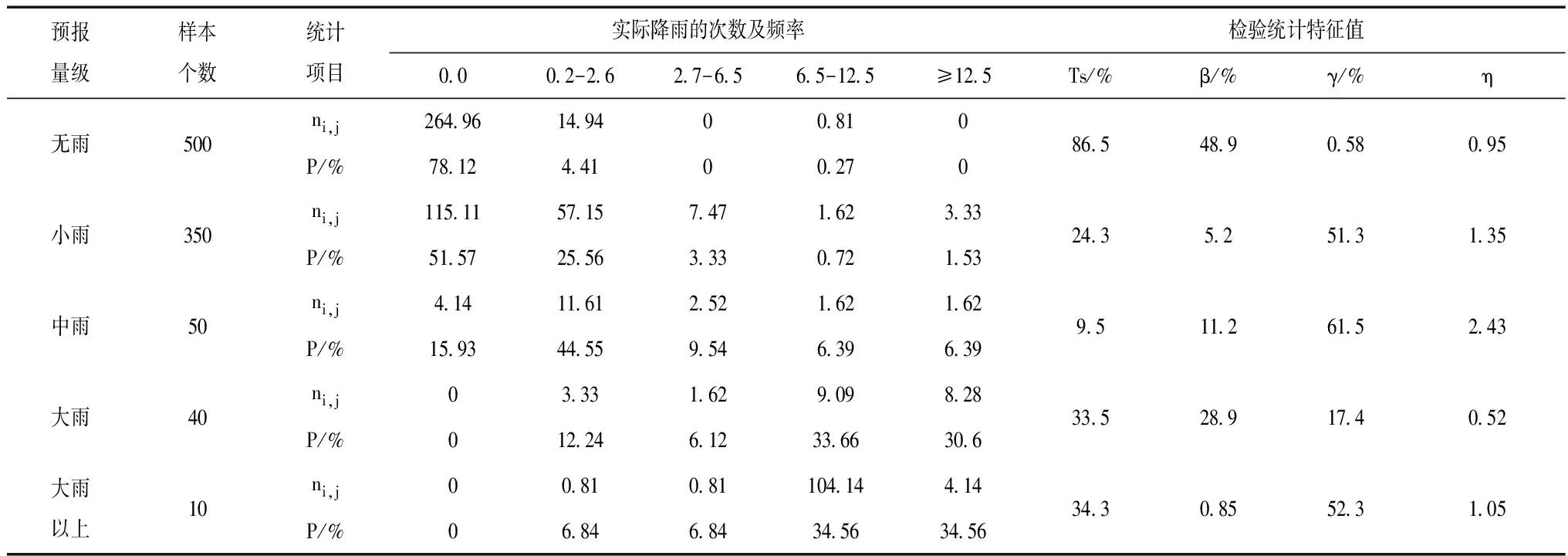
表2 未来6h不同降雨等级条件下的JMA卫星降雨与实测降雨的误差统计结果

2.3 降雨概率精度分析

在CMA和JMA两种卫星遥感降雨产品误差分析的基础上对其降雨概率分布进行统计分析，CMA卫星遥感降水产品概率统计分析，见表3；JMA卫星遥感降水产品概率统计分析，见表4。

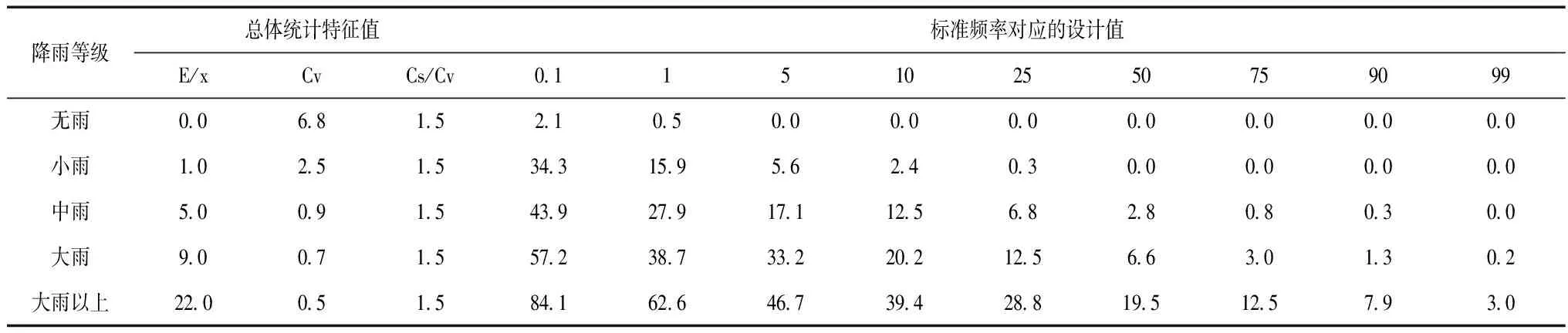
表3 CMA卫星遥感降水产品概率统计分析

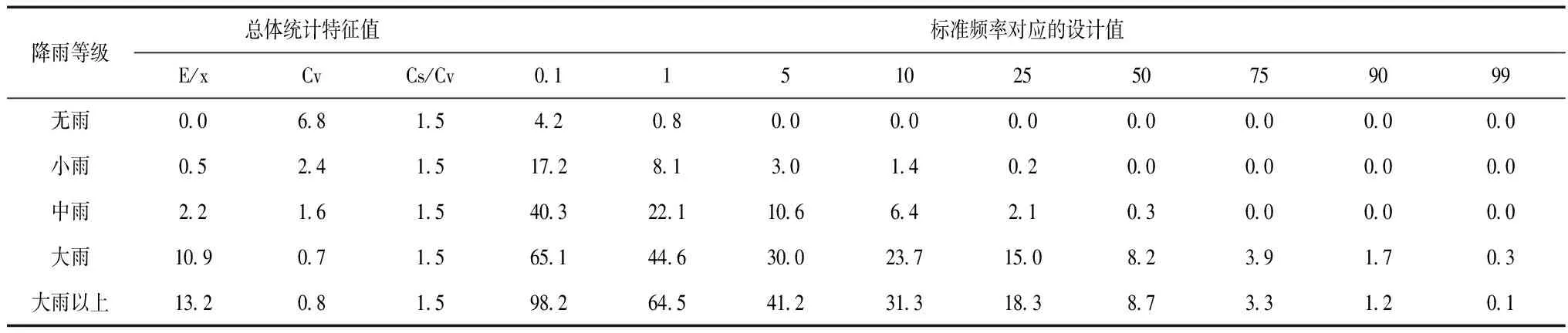
表4 JMA卫星遥感降水产品概率统计分析

从分析结果可看出，CMA和JMA两种卫星遥感降雨产品在中等雨量等级以下的概率可稳定在80%以上，而对于大雨以上等级概率均<40%，表明在辽东山区中等雨量等级下具有较好的适用性，不需要进行降雨量的修正分析，而对于大雨等级需要进行降雨量修正才能满足应用效果。此外两种卫星遥感降水产品数据的概率总体均符合标准正态分布，雨量值随着概率递减而有所减小。中等雨量变差系数要高于大雨等级的变差系数，大雨等级下卫星遥感降水产品数据的变动程度更大。

2.4 降水修正误差分析

采用卡尔曼滤波对两种卫星遥感降水数据产品进行修正，并结合实测降水数据对修正误差进行统计分析，CMA卫星遥感降水产品修正误差统计结果，见表5；JMA卫星遥感降水产品修正误差统计结果，见表6。

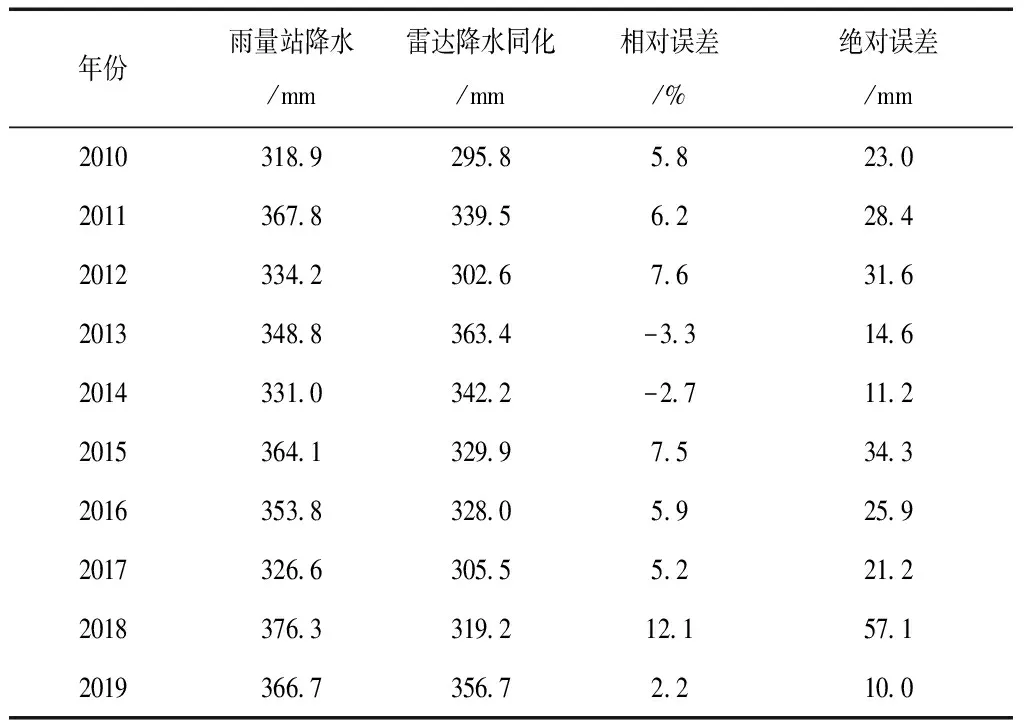
表5 CMA卫星遥感降水产品修正误差统计结果

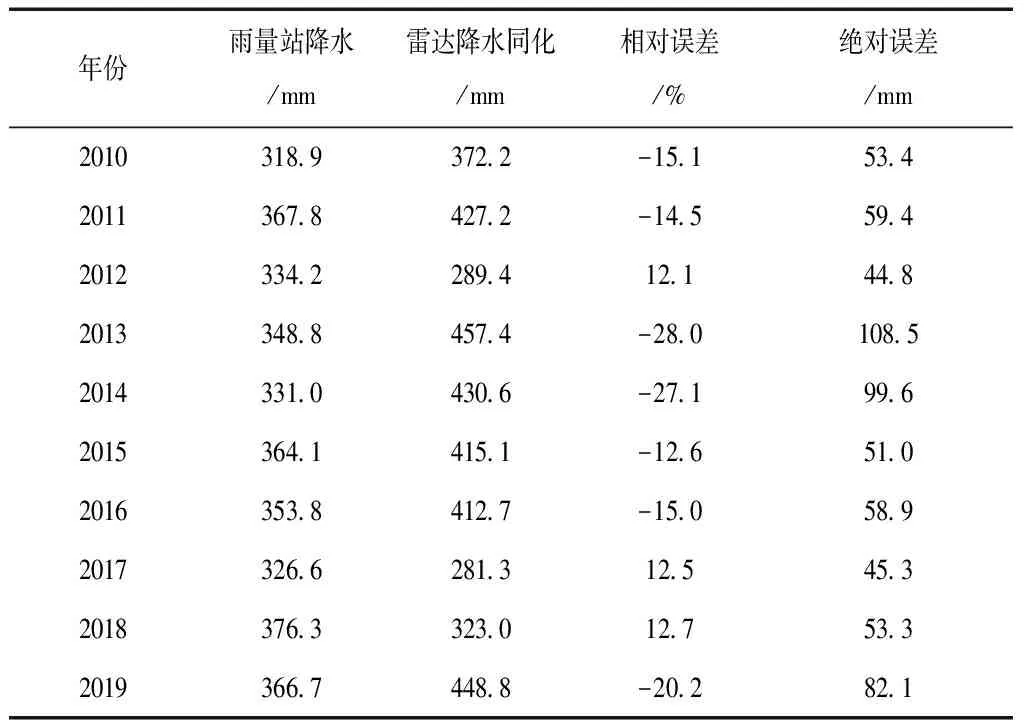
表6 JMA卫星遥感降水产品修正误差统计结果

从卫星降水产品修正误差统计结果可看出，不同卫星遥感降水产品修正后与实测降水之间的误差有所差异，CMA卫星遥感降水的修正值和实测降水值之间的误差总体±20%的主要原因在于两种卫星遥感降水产品在大雨时段具有较大误差影响所致。

2.5 水文模拟适用性分析

将修正后的卫星遥感降水产品作为水文模型的降水输入，对比分析两种遥感降水产品在辽东山区水文模拟的适用性，CMA卫星遥感降水数据修正后的水文模拟适用性分析结果，见表7；JMA卫星遥感降水数据修正后的水文模拟适用性分析结果，见表8。

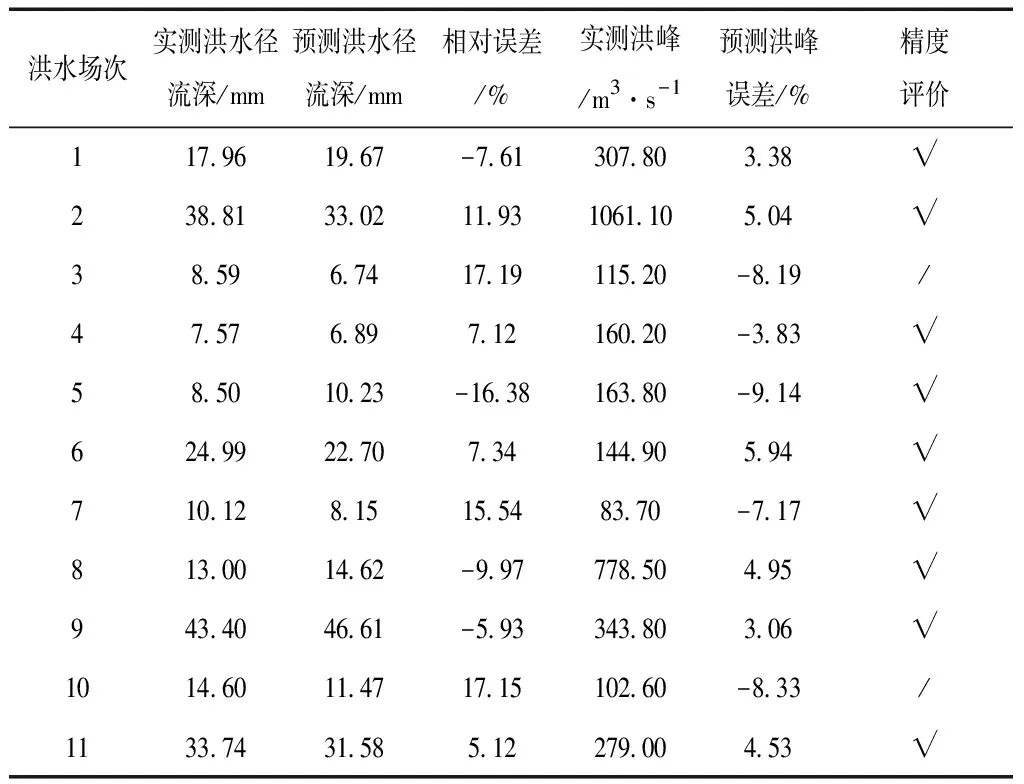
表7 CMA卫星遥感降水数据修正后的水文模拟适用性分析结果

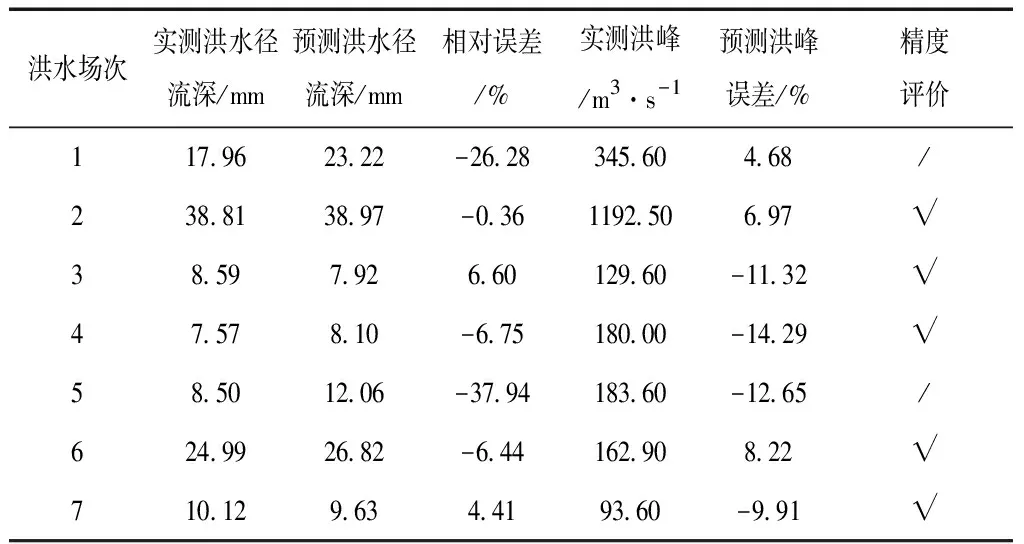
表8 JMA卫星遥感降水数据修正后的水文模拟适用性分析结果

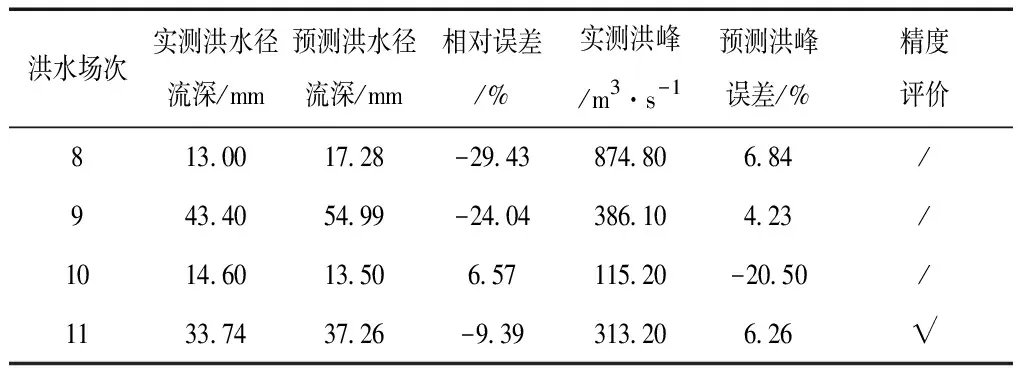
续表8 JMA卫星遥感降水数据修正后的水文模拟适用性分析结果

从两种卫星遥感降水产品修正后作为水文模型降雨输入的适用性分析结果可看出，在各场次洪水模拟的合格率总体可以在80%以上，基本达到乙级水文预报的精度要求，相比而言，CMA卫星遥感降水产品修正后的水文模拟精度要好于JMA卫星遥感降水产品修正后的水文模拟精度。

3 结 论

1)CMA和JMA两种卫星遥感降雨产品在中等雨量等级以下的概率可稳定在80%以上，而对于大雨以上等级概率均<40%，表明在辽东山区中等雨量等级下具有较好的适用性，不需要进行降雨量的修正分析，而对于大雨等级需要进行降雨量修正才能满足应用效果。

2)卡尔曼滤波可以将原始卫星遥感降水数据序列的粗差影响有所降低，并可以对不同时刻的降水量通过修正系数的调整来提升降水修正的精度，使得误差总体在可控范围内，部分年份降水修正误差>±20%的主要原因在于两种卫星遥感降水产品在大雨时段具有较大误差影响所致。

3)两种卫星遥感降水产品修正后作为水文模型降雨输入的适用性分析结果可看出，在各场次洪水模拟的合格率总体可以在80%以上，基本达到乙级水文预报的精度要求。