线控四轮转向汽车平行泊车路径规划与跟踪控制
张家旭,卜纯研,王晨,赵健†
(1.吉林大学 汽车仿真与控制国家重点实验室,吉林 长春 130022;2.中国第一汽车集团有限公司智能网联研发院,吉林长春 130011)
汽车运动学非完整约束使得经验不足的驾驶员在狭窄环境内难以完成泊车任务,而自动泊车系统是解决此问题的有效手段之一.在精确感知外界环境的前提下,泊车路径规划与跟踪控制方法是决定自动泊车系统性能的核心要素[1-2].因此,深入研究泊车路径规划与跟踪控制方法对于解决汽车运动学非完整约束导致的泊车难问题具有重要的意义.
泊车路径规划方法主要有几何规划方法[3-5]、智能规划方法[6-7]和优化规划方法[8-9].文献[3]通过圆弧、直线和回旋曲线的平移与旋转变换规划出曲率连续的泊车路径.文献[4]通过参数化Gompertz 曲线获得可执行的泊车路径.文献[5]采用圆弧-直线-β 样条曲线组合的方式规划出曲率连续的泊车路径.采用几何规划方法得到的泊车路径适用场景受限于初始泊车位姿、泊车位和不规则障碍物信息等,可行的泊车起始区域较小.文献[6]利用熟练驾驶员的泊车数据训练神经网络,使其可以模拟熟练驾驶员完成泊车任务.文献[7]利用自适应神经模糊推理系统学习熟练驾驶员的泊车操作,进而自动完成泊车任务.采用智能规划方法得到的泊车路径适用场景受限于训练样本的规模和多样性,泛化能力较弱.文献[8]将泊车路径规划问题转化为约束最优化问题,并利用高斯伪谱法求解得到最优泊车路径.为了兼顾计算效率和求解精度,文献[9]采用自适应伪谱法求解泊车路径规划问题来获得最优泊车路径.采用优化规划方法得到的泊车路径适用场景最广,但优化求解方法的较大计算量限制了其工程应用.
泊车路径跟踪控制方法主要有模型预测跟踪控制方法[10]、非线性鲁棒跟踪控制方法[11]和滑模跟踪控制方法[5,12-13].文献[10]将受控自回归积分滑动平均模型作为预测模型,采用模型预测控制方法设计泊车路径跟踪控制策略.为了抑制外界干扰和名义模型不确定性对泊车路径跟踪精度的影响,文献[11]采用非线性鲁棒控制方法设计泊车路径跟踪控制策略.文献[5]建立包含外界干扰的汽车运动学名义模型,并采用滑模自抗扰控制方法设计泊车路径跟踪控制策略.文献[12]建立非时间参考泊车路径跟踪控制模型,并基于此设计了泊车路径滑模跟踪控制策略.文献[13]采用反正切函数代替泊车路径滑模跟踪控制策略中符号函数来抑制传统滑模固有的抖振问题.上述泊车路径跟踪控制方法的被控对象均是前轮转向汽车,无法直接应用于线控四轮转向汽车.
线控四轮转向汽车具有更好的机动灵活性,在狭窄环境内更容易实现泊车操作[14].本文针对线控四轮转向汽车平行泊车场景的路径规划与跟踪控制问题,提出一种基于改进的粒子群优化算法的平行泊车路径规划方法,以及一种基于前馈控制和反馈控制的平行泊车路径跟踪控制策略.首先,综合考虑线控四轮转向汽车运动学非完整约束、动力总成子系统和转向子系统的过程约束和边界约束、直线交点法描述的避障约束、泊车的初始位姿和目标位姿约束,建立以最小化平行泊车过程总时长为目标的平行泊车路径规划约束最优化问题,并采用可以有效处理等式约束和不等式约束的粒子群优化算法对其进行求解,进而得到最优平行泊车路径.随后,利用平行泊车路径规划过程得到的前轮转向角和后轮转向角作为前馈控制量,并利用汽车实际位姿与期望位姿的偏差构建PI 反馈控制量,实现对规划的平行泊车路径快速、精确和稳定的跟踪控制.最后,利用车辆动力学仿真软件构建模型在环仿真系统,验证所提出的线控四轮转向汽车平行泊车路径规划方法和路径跟踪控制策略的可行性和有效性.
1 平行泊车路径规划
1.1 平行泊车路径规划问题描述
线控四轮转向汽车平行泊车过程中处于低速大转角行驶状态,可认为四个车轮无侧偏的绕同一瞬时圆心做圆周运动.如图1 所示,将线控四轮转向汽车后轴中点作为参考点,建立其平行泊车过程中的运动学方程为:
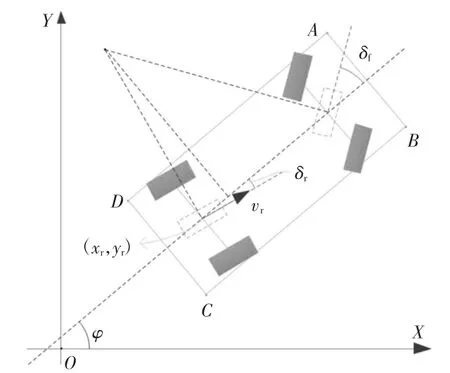
图1 线控四轮转向汽车运动学模型Fig.1 The wire-four-wheel steering vehicle kinematic model
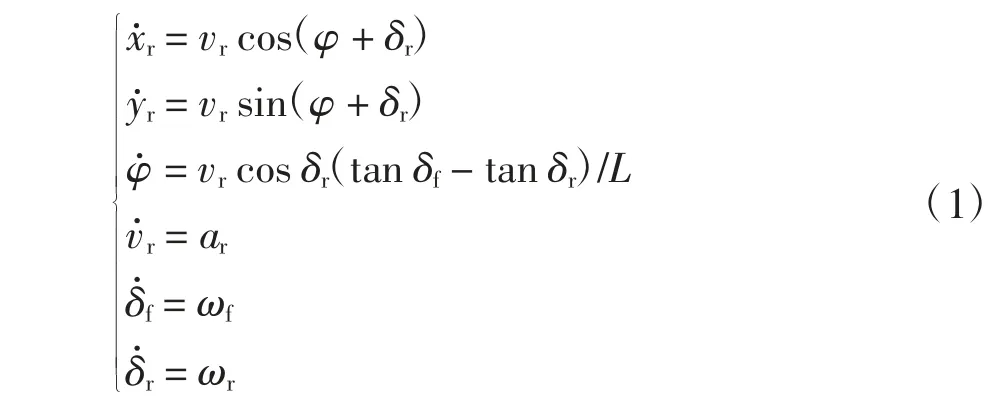
式中:xr、yr、vr和ar分别为线控四轮转向汽车后轴中点横坐标、纵坐标、速度和加速度;δf和δr分别为线控四轮转向汽车前轮和后轮转向角;ωf和ωr分别为线控四轮转向汽车前轮和后轮转向角速度;φ 和L分别为线控四轮转向汽车方位角和轴距.
定义系统状态向量和控制向量为:
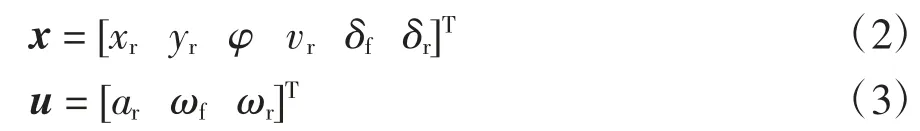
利用式(2)(3)将式(1)重写为:

利用四阶龙格库塔积分法将式(4)离散化为[15]:
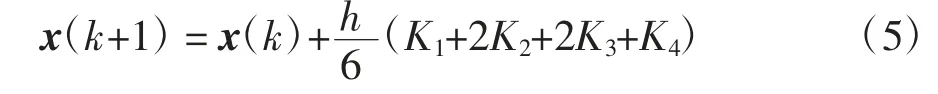
式中:计算步长h 与系数K1、K2、K3和K4可分别表示为
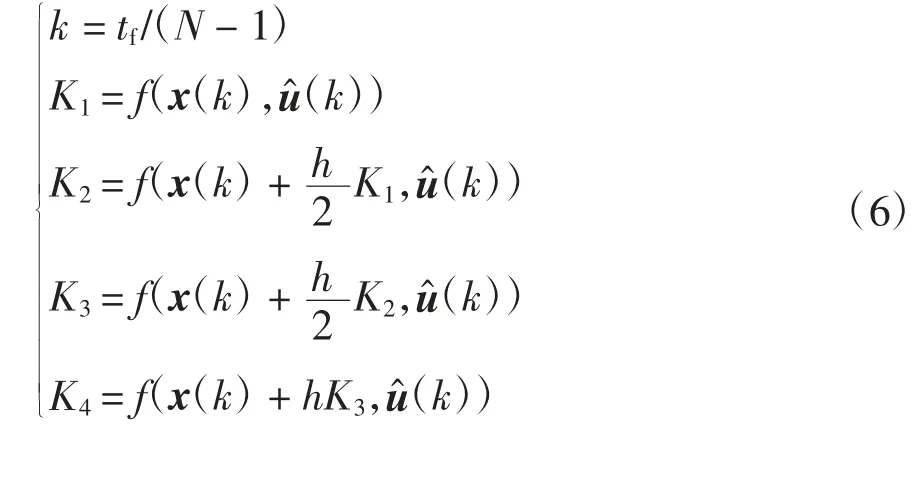
式中:tf和N 分别为平行泊车过程总时长和离散点数量(k)=(u(k)+u(k+1))/2.
考虑线控四轮转向汽车动力总成子系统和线控四轮转向子系统的过程约束和边界约束,可得:

式中:vrmax和armax分别为线控四轮转向汽车后轴中点速度和加速度最大值;δfmax和δrmax分别为线控四轮转向汽车前轮和后轮转向角最大值;ωfmax和ωrmax分别为线控四轮转向汽车前轮和后轮转向角速度最大值.
基于汽车后轴中点坐标和方位角可得如图1 所示的汽车轮廓四个顶点A、B、C 和D 的坐标为:
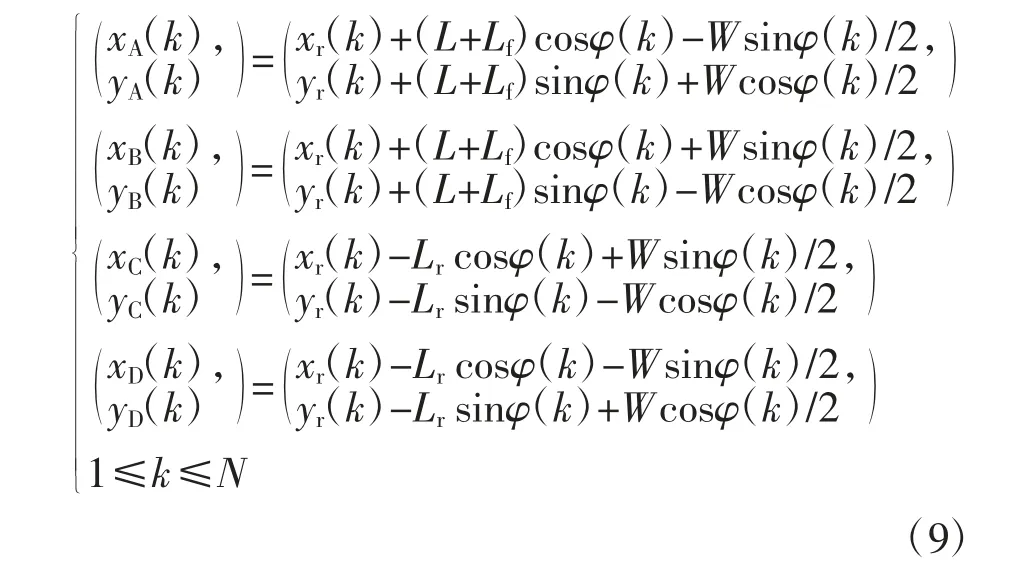
式中:Lf、Lr和W 分别为汽车前悬、后悬和宽度.
汽车平行泊车过程中其轮廓边缘AB 与如图2 所示的泊车位前方障碍物无碰撞的约束条件可表示为:
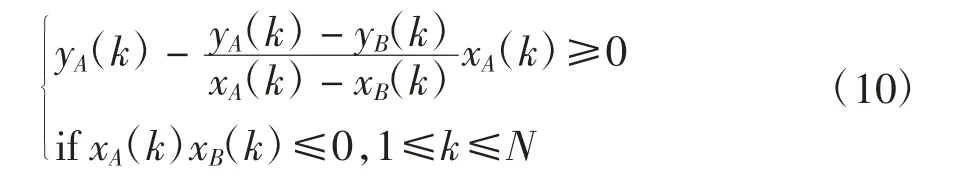
汽车平行泊车过程中其轮廓边缘BC 与如图2 所示的泊车位前方障碍物无碰撞的约束条件可表示为:
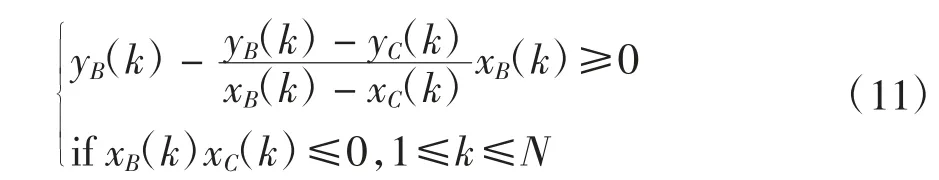
汽车平行泊车过程中其轮廓边缘BC 与如图2 所示的泊车位侧方路基无碰撞的约束条件可表示为:

式中:Wp为平行泊车位宽度.
汽车平行泊车过程中其轮廓边缘CD 与如图2 所示的泊车位后方障碍物无碰撞的约束条件可表示为:
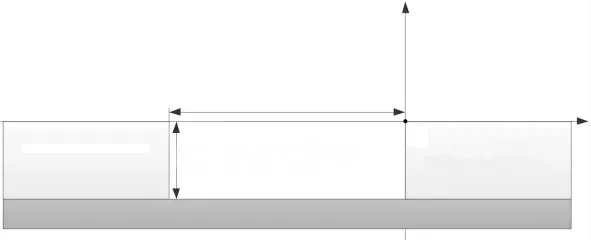
图2 平行泊车位Fig.2 Parallel parking slot
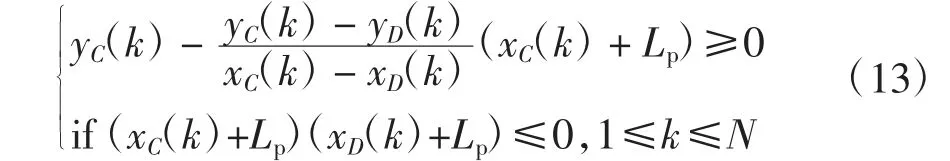
式中:Lp为平行泊车位长度.
已知平行泊车的初始位姿和目标位姿分别为(x0,y0,φ0)和(xf,yf,φf),则有
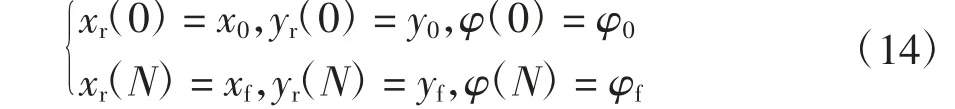
将式(5)、式(8)和式(14)描述的等式约束条件记为c(x,u)=0,将式(7)、式(10)~式(13)描述的不等式约束条件记为g(x,u)≤0,则平行泊车路径规划问题转化为以平行泊车过程总时长为目标的约束最优化问题,使线控四轮转向汽车在最短时间内完成平行泊车任务.

由式(6)和式(15)可知,给定离散点数量N,最小化平行泊车过程总时长tf约束最优化问题可等价为最小化计算步长h 约束最优化问题.
1.2 平行泊车路径规划问题求解
粒子群优化算法是一种基于启发式信息的随机搜索算法,具有收敛速度快和设置参数少等优点,特别适用于无约束最优化问题求解[16].本节利用最优化问题的约束条件改进粒子群优化算法的适应度函数,使改进的粒子群优化算法可以求解式(15)描述的平行泊车路径规划约束最优化问题.已知系统控制向量u(k),1≤k≤N 包含三个分量,则表征系统控制向量的粒子位置向量和速度向量包含3N 个分量.若按照第一个系统控制向量三个分量至最后一个系统控制向量三个分量先后方式排序,则第i 个粒子的位置向量和速度向量可分别表示为:
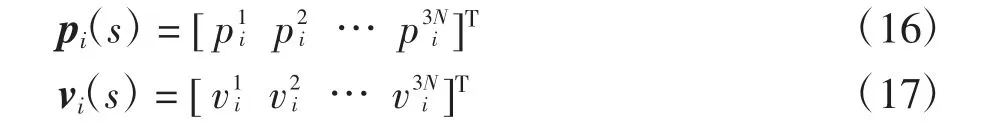
式中:s 为粒子群优化算法的当前迭代次数.
利用第i 个粒子的历史最优解pbest
i(s)和群体的历史最优解pbest(s)更新第i 个粒子的速度为:
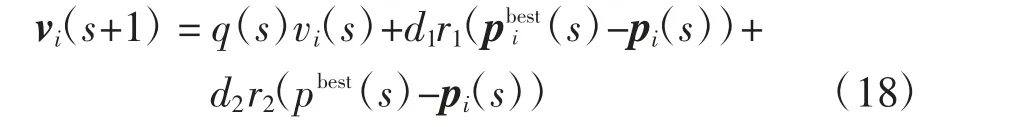
式中:r1,r2∈[0,1]为均匀分布的随机数;d1和d2分别为粒子速度自身部分和社会部分权重系数,二者的有机组合可以使粒子群优化算法保持收敛速度和搜索效果的均衡;q(s)为控制粒子历史速度对当前速度影响的惯性部分权重系数,可表示为:
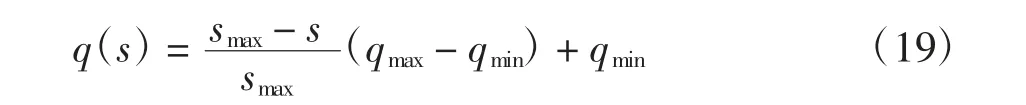
式中:qmax和qmin分别为惯性部分权重的最大值和最小值;smax为总迭代次数.通过自适应调整惯性部分权重系数,使粒子群优化算法在前期有较高的全局搜索能力,在后期有较高的局部搜索能力.
利用第i 个粒子在迭代计算次数s+1 的速度更新其位置为:

利用最优化问题的约束条件计算第i 个粒子的适应度函数为:
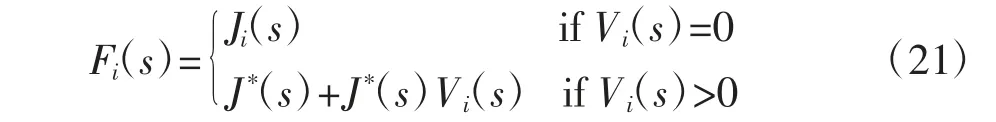
式中:Ji(s)为第i 个粒子在迭代计算次数s 的优化目标值;J*(s)为第i 个粒子的历史最差优化目标值;Vi(s)表示为
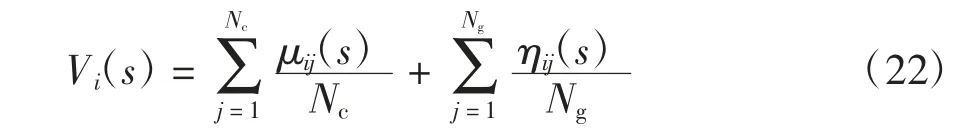
式中:Nc和Ng分别为最优化问题等式约束条件数量和不等式约束条件数量;μij(s)和ηij(s)表示为
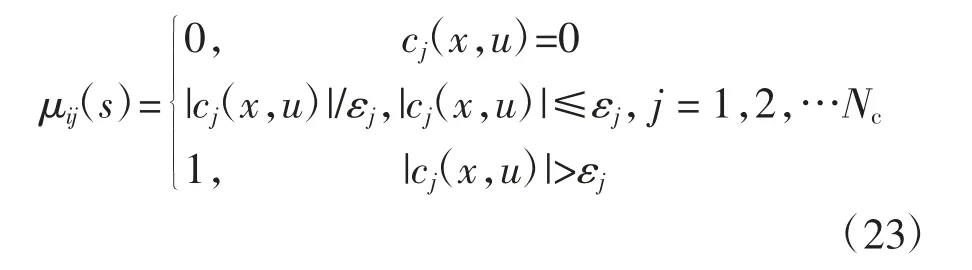
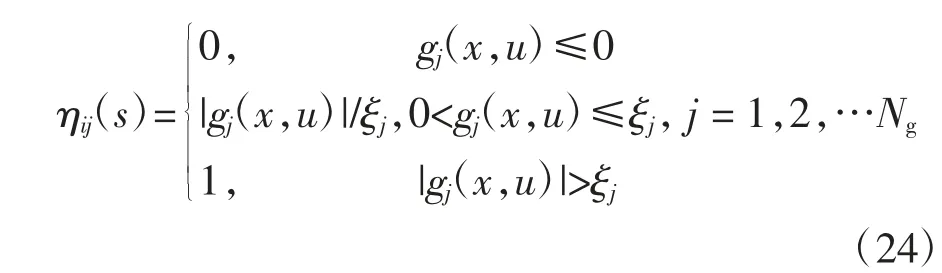
式中:εj和ξj分别为最优化问题等式约束条件允许的容差和不等式约束条件允许的容差.
综上所述,可得如图3 所示的基于改进的粒子群优化算法求解平行泊车路径规划约束最优化问题的具体流程.

图3 改进的粒子群优化算法Fig.3 Improved particle swarm optimization algorithm
2 平行泊车路径跟踪控制
本节基于前馈控制和反馈控制相结合的方式设计平行泊车路径跟踪控制策略.其中,前馈控制环节用于提高平行泊车路径跟踪控制策略的响应速度和精度,而反馈控制用于抑制外界扰动对平行泊车路径跟踪控制性能的影响.
如图4 所示,首先利用汽车实际位置与期望位置的偏差eD(k)、汽车实际方位角与期望方位角的偏差eφ(k)计算前轮转向角反馈控制量为:
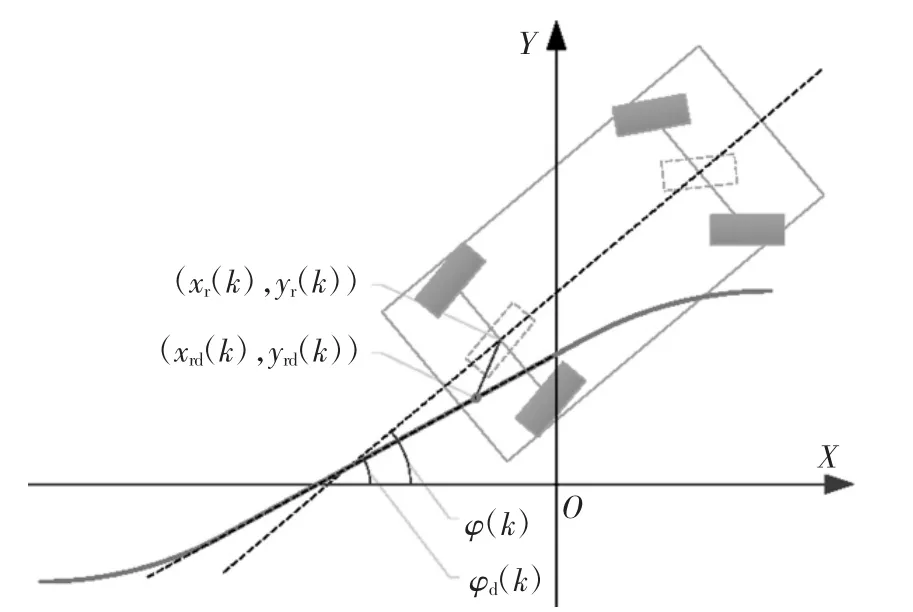
图4 平行泊车路径跟踪控制Fig.4 Parallel parking path tracking control

式中:KPD和KID分别为汽车实际位置与期望位置偏差的比例系数和积分系数;KPφ和KIφ分别为汽车实际方位角与期望方位角偏差的比例系数和积分系数;eD(k)和eφ(k)可表示为:
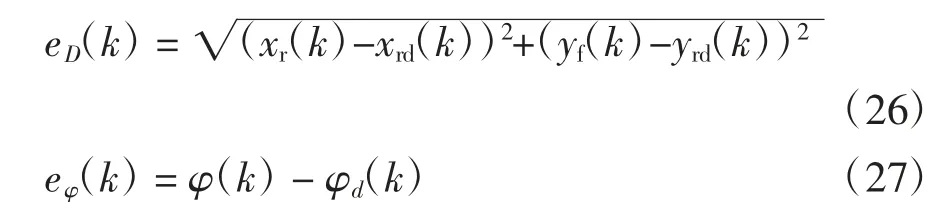
式中:(xr(k),yr(k),φ(k))和(xrd(k),yrd(k),φd(k))分别为汽车实际位姿和期望位姿.
若平行泊车路径规划过程得到的汽车前轮转向角前馈控制量为δfd(k+1),则汽车前轮转向角控制量可表示为:

由汽车前轮转向角最大值与后轮转向角最大值的比例关系,可得汽车后轮转向角控制量为:
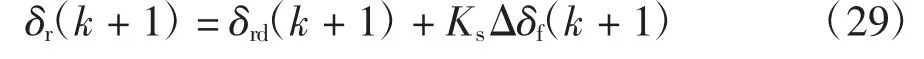
式中:δrd(k+1)为汽车后轮转向角前馈控制量;Ks=δrmax/δfmax为比例系数.
3 仿真分析
本节利用车辆动力学仿真软件建立线控四轮转向汽车平行泊车路径规划与跟踪控制方法的模型在环仿真系统,对其可行性和有效性进行验证.以天津一汽夏利N5 整车参数为基础设计线控四轮转向汽车的仿真参数为L=4.155 m,W=1.645 m,Lf=0.8 m,Lr=0.95 m,vrmax=1 m·s-1,armax=2 m·s-2,δfmax=0.524 rad,δrmax=0.087 3 rad,ωfmax=ωrmax=0.524 rad·s-1;依据工程经验,仿真验证过程中粒子群优化算法的基础参数分别设置为d1=1.2,d2=1.5,qmin=0.3,qmax=1.5,smax=1 000 和εj=ξj=10-3,种群规模设置为30、粒子速度向量边界区域设置为[-1,1]、粒子位置向量中表征汽车后轴中点加速度信息的分量的边界区域设置为[-armax,armax],粒子位置向量中表征汽车前轮转向角速度信息的分量的边界区域设置为[-ωfmax,ωfmax],粒子位置向量中表征汽车后轮转向角速度信息的分量的边界区域设置为[-ωrmax,ωrmax],算法迭代收敛判断容差设置为10-4;仿真结果如图5所示.
如图5(a)(b)所示,采用基于改进粒子群优化算法的平行泊车路径规划方法得到的平行泊车路径可以安全、舒适地引导线控四轮转向汽车进入平行泊车位,并且目标平行泊车路径曲率的连续性有效避免了线控四轮转向汽车原地转向现象.
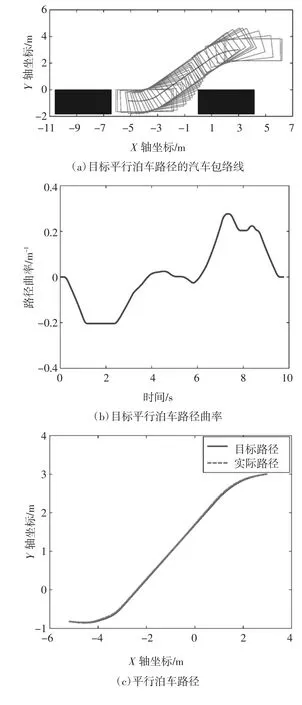
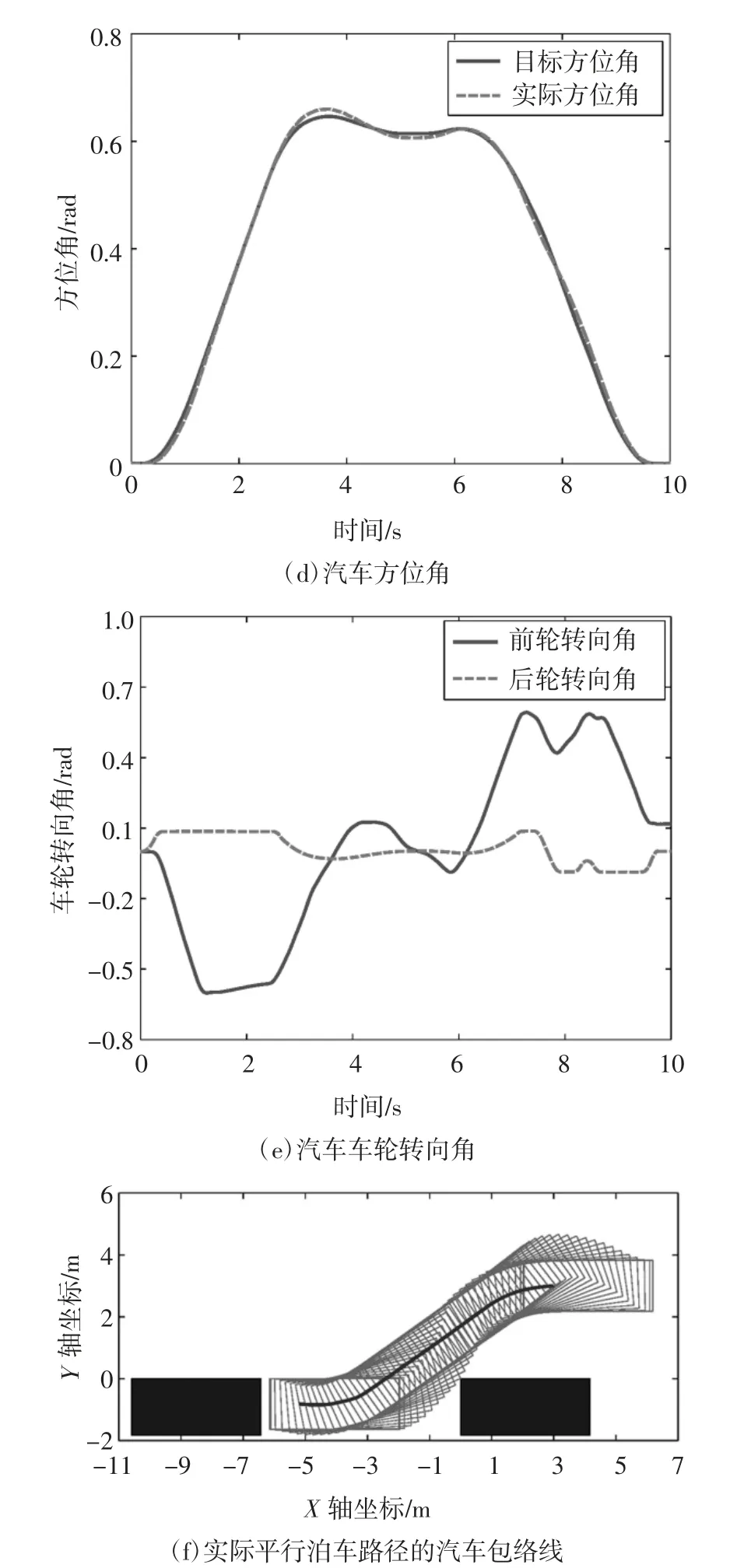
图5 仿真结果Fig.5 Simulation results
如图5(c)~(f)所示,采用基于前馈控制和反馈控制相结合方式设计的平行泊车路径跟踪控制策略可以使线控四轮转向汽车快速、精确和稳定地跟踪目标泊车路径,进而安全无碰撞地完成平行泊车任务.
4 结论
本文提出了一种线控四轮转向汽车平行泊车路径规划与跟踪控制方法.综合考虑了线控四轮转向汽车运动学非完整约束、动力和转向子系统约束、避障约束和泊车位姿约束,建立了平行泊车路径规划约束最优化问题,并采用可以改进的粒子群优化算法对其进行求解来获得最优平行泊车路径.采用前馈控制和PI 反馈控制相结合的方式设计了平行泊车路径跟踪控制策略,实现对规划的平行泊车路径快速、精确及稳定的跟踪控制.利用车辆动力学仿真软件构建模型在环系统,验证所提出的线控四轮转向汽车平行泊车路径规划与跟踪控制方法的可行性和有效性,结果表明:所提出的方法可以快速、精确、稳定地引导线控四轮转向汽车自动完成平行泊车任务.

