人眼亮度感知特性在高动态范围影像中的应用

石雅婷 顾晓娟

(1.北京电影学院中国电影高新技术研究院,北京 100088)

(2.北京电影学院影视技术系,北京 100088)

1 引言

伴随着生产材料和制作工艺的进步,近年来高动态范围(HDR,High Dynamic Range)影像逐渐在电影电视行业形成一股新的浪潮。高质量的影像画面需要具备五个基本要素,分别是:分辨率(Resolution)、位 深 (Bit Depth)、帧率 (Frame Rate)、色域 (Color Gamut)和亮度 (Brightness),除亮度外,其余四部分均在BT.2020 的4K/8K 标准中做出了相应的规定。相较于传统的标准动态范围 (SDR,Standard Dynamic Range)显示,HDR 显示技术通过提升画面峰值亮度,控制最低显示亮度和拓宽色域,实现了更高的动态范围和对比度,覆盖更大的色彩空间,呈现出更丰富的影像内容,极大地提升了观众的视觉体验。

数字图像的获取、制作和重现离不开光信号与电信号之间的相互转换。获取图像时最理想的情况是记录无损原生数据,但受限于存储位深影响,需要研究人眼对亮度的感知特性,尽可能保留更多的有效亮度信息;使用制作后的数据重现画面时,为了避免出现肉眼可见的亮度阶梯,显示端系统的显示能力应该高于人眼对亮度的感知阈值。由此可见,研究人眼的亮度感知特性对数字内容的制作、传递函数及采样位深的选取都具有非常重要的指导意义。然而影响人视觉亮度感知的因素有很多,测量条件变化时,影响因子也在变化,人眼对画面的感知和评价不仅有客观因素影响,还有主观心理层面的影响,因此模拟人眼视觉系统的亮度感知是个极其复杂的过程。

本文对人眼亮度感知模型的研究进行了详细梳理,简述了其在当今影视领域的应用,并基于高动态范围(HDR)显示技术逐渐兴起的现状,对人眼亮度感知的相关研究是否仍然适用做出了讨论。

2 人眼亮度感知相关模型及其在影视中的应用

不论电影还是电视,最终的画面是呈现给观众的,视频画面质量的评价标准归根结底就是得到观众的认可,人眼的视觉特性及心理因素在其中起到了决定性的作用。人类视觉系统 (HVS,Human Visual System)对视频图像处理和计算机视觉的研究至关重要,很多技术都建立在对视觉感知系统机理和特性的了解上,例如利用人眼色彩分辨率远低于亮度分辨率的特点,使用色度二次采样将颜色压缩进信号里,减少带宽;利用人眼对画面暗部的亮度变化更敏感的特性在有限带宽下更有效地存储亮度信息;在数字图像压缩中,利用人眼看不到高频细节的特点,亮部分配较少位深却不会造成质量明显的损失等。人类视觉系统有着多种特性:亮度非线性、对比度敏感、空域掩模效应和多通道特性等。随着人们对视觉系统研究的深入,人眼视觉模型也在不断更新。

2.1 人类视觉系统(HVS)

人类通过视觉获取的外界信息占所有获取信息的60%以上,通过人眼从可见光中感知亮度和颜色信息。人眼的视网膜中含有约1.3 亿个感光细胞,称为光感受器。感光细胞又分为视锥细胞 (cones)和视杆细胞(rods)两种,视锥细胞的数量大约有600～800万个,对强光敏感,有颜色感知,光敏度低但视敏度高。视杆细胞大约有1.25亿个,对弱光敏感,无颜色感知,光敏度高但视敏度低。研究表明人眼可以感知从3.18×10nit到3×10nit共11个数量级的亮度,其中10～10nit 是暗视觉(scotopic vision),在这一视觉模式下只有视杆细胞活跃,10～3nit是中间视觉 (mesopic vision),这阶段视锥细胞和视杆细胞都很活跃,3～10nit被称为明视觉 (photopic vision),该模式下仅视锥细胞活跃。

人眼类似于一个光学系统,但它不是普通意义上的光学系统,还受到心理和神经系统的影响,面对同一亮度时,不同的人心理感知量不同,对同一个人来说,从0nit增到5nit和从50nit增到55nit带来的亮度变化感受也不同,因此研究人眼视觉模型时还需要应用到心理物理学实验的方法。在心理物理学中,建立物理量和感知量的关系模型主要有韦伯定律和史蒂芬斯幂定律两种。

图1 三种视觉模式及对应的亮度范围

2.2 韦伯定律、史蒂芬斯幂定律及其应用

韦伯(1834)通过研究触觉发现,在一定的重量I下,能让人感知到有重量变化时,增加的最小重量△I与I成正比,比例常数为K:

这一定律被称为韦伯定律(Weber’s law),临界值△I被称为最小可觉差 (JND,Just noticeable difference),常数K 被称为韦伯比 (Weber ratio)。对于不同的感官刺激,韦伯比K 不同。将式 (1)左右同时积分即可得到:

其中K是常数。图2是人眼的亮度感知特性曲线,横坐标是亮度I,纵坐标表示感知量S,函数关系符合式(2),由图可以看出,在暗部和亮部同样的亮度变化带来的感觉差异是不同的。当亮度降低时,可感知到亮度变化的最小可觉差减小,人眼对亮度变化越敏感。

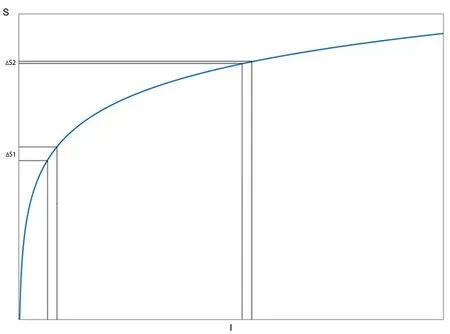
图2 人眼的亮度感知特性曲线

值得注意的是,在消色差感知的实验中,韦伯定律仅在中间亮度范围有效,在非常暗或非常亮的刺激下,韦伯比均偏离理论值。实际上人眼在场景亮度为1nit以下或1000nit以上时,感知亮度反差的灵敏度会变小,如果考虑到极端情况,史蒂芬斯幂定律的模型会更适用。

史蒂芬斯 (1961)总结了史蒂芬斯幂定律:人类感知在很大范围内是符合幂定律的。在实验中,实验人员提供标准刺激和其相对应的数值,受试者说出比较刺激相对于标准刺激的估计值,得出结论感知量S与物理刺激I之间是幂函数的关系:

其中k是比例常数,指数a是取决于刺激形式的常数,针对不同的物理刺激a值不同。a小于1时,感知量与物理量的关系与韦伯定律结论相似,a大于1时,感知量与物理量的关系与韦伯定律相反。与史蒂芬斯幂定律可以归属为一类的还有De Vries-Rose模型,这一模型单独考虑暗光处,亮度平方根均匀增加,感知均匀增加。

因此在常见的1nit～1000nit以内,韦伯模型模拟得很好,仅考虑暗处 (例如3nit 以下)时,De Vries-Rose模型模拟较好,在极暗和极亮场景下,使用史蒂芬斯幂模型较好。

虽然韦伯定律出现得比史蒂芬斯幂定律早,但最早应用在影视领域的是史蒂芬斯幂定律,最主要的原因是当时使用的显示器的限制。早在模拟视频时代,模拟摄像机常采用摄像管将被摄景物的光信号转换为与亮度成比例的电脉冲信号,这种光信号与电信号之间的转换是线性的。重现图像时,CRT(Cathode Ray Tube,阴极射线管)显示器根据输入的电压信号,利用电子枪发射电子轰击荧光层,通过空间混色还原影像画面。由于CRT 自身的特性,从电压转换为亮度时是非线性的指数关系,表现为:亮度=输入,此处的γ就是CRT 伽马。这与人眼的亮度感知特性恰好相反,如果直接将摄像管输出的电压信号放大传送给CRT 显示器,会造成明显的非线性失真,画面整体反差增大,亮度降低。为了补偿显示端的非线性,需要在摄像机里加入编码伽马使设备正确还原图像,这一过程称为伽马校正。伽马校正可以表示为:

伽马校正的作用主要体现在:

(1)补偿CRT 自身的非线性失真。经过CRT伽马和伽马校正后的总伽马就是系统伽马,理想状况下系统伽马等于一。

图3 伽马校正

(2)使电压和亮度呈非线性关系符合人眼亮度感知特性。由于多数情况下重现影像的平均亮度和对比度都远远低于被摄场景以及原始场景和观看场景不同等原因,实际应用中系统伽马均大于1,如图4所示,是一条略微向下弯曲的曲线,例如在全黑环境中,符合史蒂芬斯幂定律,电影院中系统伽马为1.5,系统伽马越大,画面的对比度饱和度越大。

图4 大于1的系统伽马样例

1990年,柯达公司发明了胶片扫描系统Cineon System 采用10bit log函数记录设计,log形式编码这才进入人们视野,随着大规模集成电路和半导体存储技术的发展,我们进入数字时代。获取数字图像时,数字摄像机大多使用CCD (charge-coupled device,电荷耦合元件)或CMOS (complementary metal oxide semiconductor,互补金属氧化物半导体)感光元件将光信号转换为电信号,亮度由离散的数字表示,这种线性转换关系下相邻码值间的亮度变化相同,不符合人眼的亮度感知特性,同时电影摄像机也想要获得类似胶片的特性和后期调整方式,根据韦伯定律的结论,市面上的数字摄像机通常会使用对数函数作为自己的OETF,表示为:

其中I是输出编码,I是传感器捕获到的线性图像,a、b、c、d是实数值,不同的相机制造商和相机设置会有不同。如今在不同的摄影机厂家系统内可以看到以log函数为基础变形的各种OETF,例如SONY 公司的S-Log2:

其中a、b、c、d、e、f及cut在不同曝光指数(EI)有对应数值。

Canon公司的Clog:

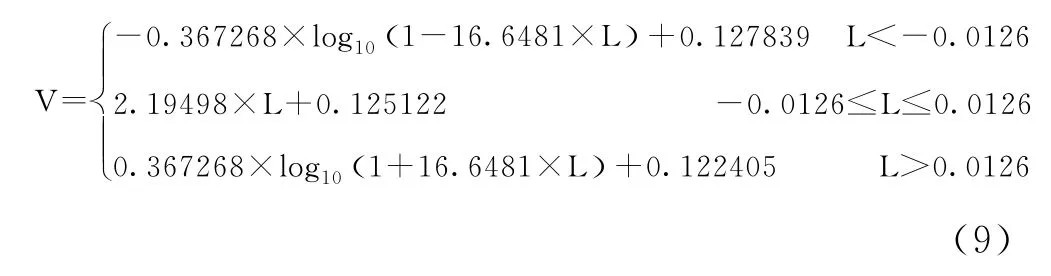
以及Panasonic的V-Log:

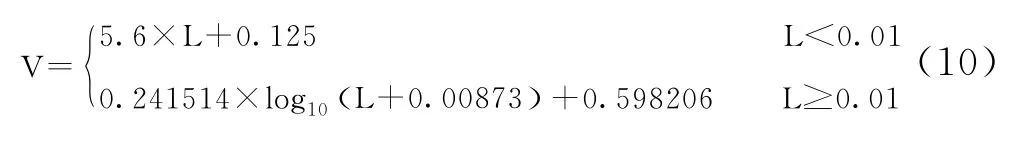
各厂家OETF的示意图见图5。

图5 常见的几种OETF

经过非线性编码后,在暗部区域就有了更多的码值范围表示,更符合人眼在暗环境下对亮度变化更敏感的特性。

2.3 人眼对比敏感度模型及其在HDR 影像中的应用

Campbell和Robson (1968)提出人眼感知对比度变化的能力取决于刺激的空间频率,由此引申出视觉系统具有多个空间通道,每个通道都有不同的空间频率,并且可以通过多个空间滤波器进行模拟。每个通道都有独自的滤波器,通道携带的信号由输入的刺激和对应感受器的卷积核得到。因此,描述视觉系统的特征就是找到卷积核,求卷积核的傅立叶变换也就是求人眼的对比敏感度函数 (CSF,Contrast Sensitivity Function)。

Barten (1999)发表论文指出,CSF 很大程度上取决于亮度 (luminance)、视角 (visual angle)、周围环境以及其他的生理因素,例如眼睛的质量、瞳孔直径和感光细胞的灵敏度等,他根据前人相关实验得出的数据,综合考虑了所有的影响因素后给出了一个人眼对比敏感度函数的极其复杂的数学模型:

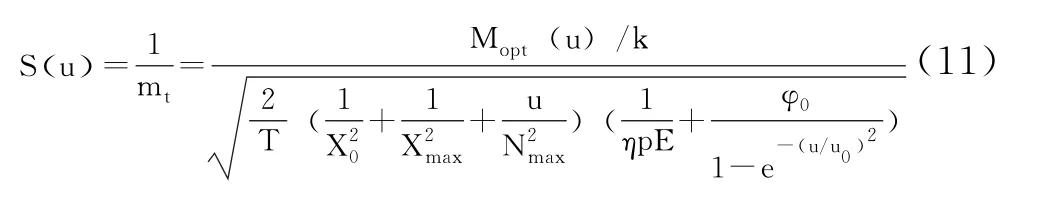
此模型成立的前提是基于人眼对比敏感度主要由视觉系统的内部噪声影响这一假设,因此考虑了很多生理因素影响,例如:M是考虑了眼睛屈光介质中的杂散光、视网膜漫射和接收器的离散结构卷积后产生的眼睛光学MTF,E 是视网膜照度,k是眼睛的信噪比等,其中许多参数都是定值,计算方法在文献[5]中有详细说明,此处不再赘述。这一模型可以模拟不同实验环境的多种心理物理数据。

2003年Barten 又给出了这个模型的简化版本,后来被广泛地应用于数字影像领域,现在被称为Barten CSF:

其中对比敏感度S为因变量,影响因子仅有空间频率u (cycles/degree)、视角X、亮度L。固定视角X,对于亮度L,取空间频率u满足:

即可得到视觉灵敏度函数S (L)仅关于亮度L的函数。

图6 不同亮度水平下的Barten曲线

2004年Cowan 等人在研究“对比敏感度对位深影响”的研究中将Barten函数分为Barten Ramp(阶梯状信号)和Barten Flat(方波信号)两种,通常使用Barten Ramp来评估EOTF,图7描述了当前亮度下人们开始看到亮度色阶的对比度阈值,Barten Ramp曲线以上看不出亮度色阶,以下区域表示可以看到亮度色阶。

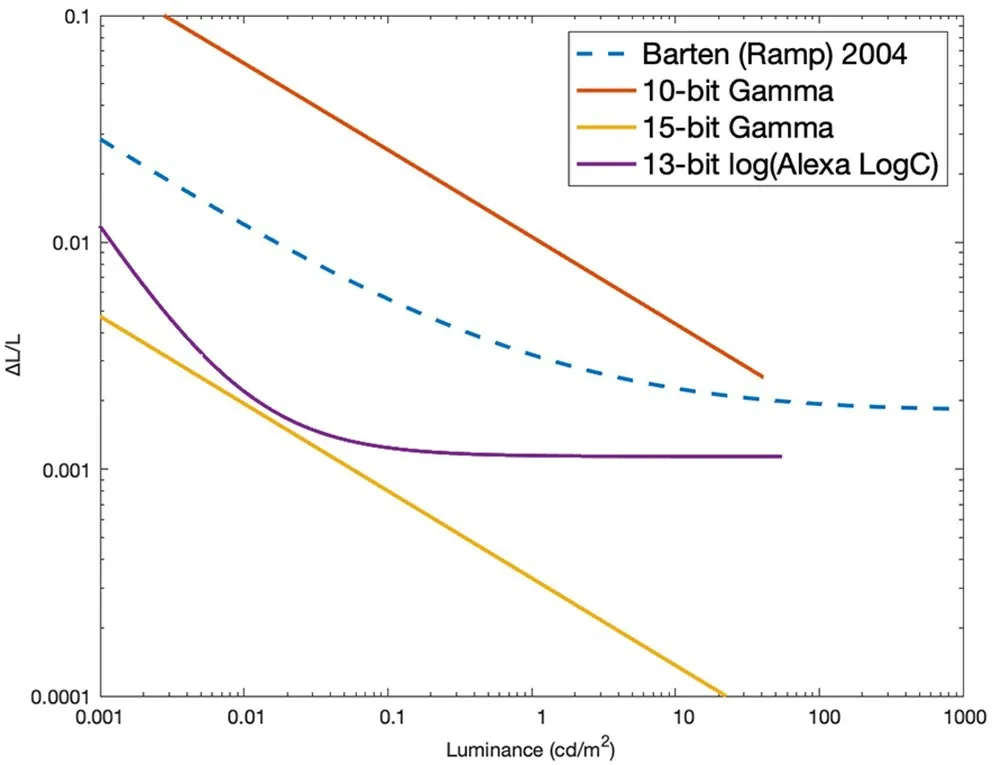
图7 10bit伽马、15bit伽马与13bitlog编码对比

为了提升画面质量,我们希望画面的对比度永远低于Barten阈值,如果使用伽马做传递函数,采样位深需要达到15bit,这对消费级别的显示器来说是很高的要求,并且无法有效利用数据,画面中高部亮度范围的位深都浪费了。13bit的Log编码图像虽然也在Barten阈值以下,但分配在暗部的位深远大于需求量。

2014年杜比实验室根据Barten 的人眼视觉特性模型开发了感知量化 (PQ,Perceptual Quantization)编码,采用绝对亮度体系,将最高10000nit的亮度按照人眼对亮度的感知特性量化编码,记录亮度的绝对值,用绝对亮度再现被摄景物。PQ 将视角控制在40度,选择每个亮度等级下最敏感的空间频率点,根据人眼视觉系统对亮度的感知对比度来最大限度利用编码空间对数字信号进行量化,简单来说,就是在尽量避免出现人眼可察觉的亮度色阶(banding)的情况下对数据进行量化和编码。

PQ OETF是PQ EOTF 的逆函数,PQ EOTF的公式如下:

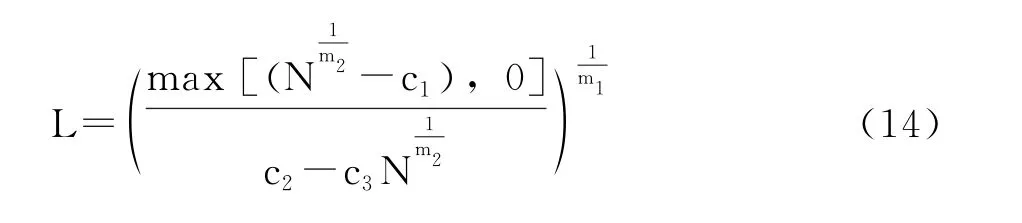
其中N∈ [0,1]表示非线性色彩值,L∈[0,1]表示相应的线性色彩值,m、m、c、c、c是常数:

由于PQ EOTF 定义的最大显示亮度为10000 cd/m,因此相应的线性光输出C=10000*L,C的单位为cd/m。PQ 传递函数最大化了人类视觉亮度的编码效率,仅使用12位信号就可以覆盖0.001～10000nit的信号,没有明显的带状或阶梯状伪影。实际上,尽管Barten在建立数学模型时使用到了不同亮度等级的多个数据,但所有数据的最大亮度只有500cd/m。因此基于Barten CSF 的PQ 曲 线 并未通过实验证明大于500 cd/m的数据准确性。

除去人类视觉系统内部的生理因素影响,外部环境光同样会对人眼视觉灵敏度有影响。2003 年Barten引入了环境光影响CSF的校正因子,校正因子的大小取决于周围环境的亮度,并且必须乘以CSF。校正因子的公式如下:

其中L是物体亮度,L是环境光亮度,X是可视角度,校正因子存在的原因是人眼对周围环境有适应能力,当周围环境的亮度比测试图案亮度高或低得多,对比敏感度会大大降低,这一因素PQ并未考虑。

除此之外,2015年BBC和NHK 还共同研发了一种向下兼容SDR 格式的标准:HLG (Hybrid Log Gamma,混合对数编码),是一条基于典型亮度感知模型的曲线,被认为是针对电视广播信号的最佳HDR 技术。HLG 的OETF公式如下:

其中I是与场景线性光成比例的、根据摄像机曝光量归一化的电平值,范围是 [0,1],a、b、c分别是常数值,a=0.17883277,b=1-4a=0.28466892,c=0.5-a*ln (4a)=0.55991073。前面讨论过在中间和较高亮度时韦伯定律适用,因此I≥1/12部分使用对数函数,亮度较低时史蒂芬斯幂定律更好,I≤1/12部分采用幂函数,伽马为0.5。HLG 的EOTF 是HLG OETF 的逆函数。2016 年Borer 和Cotton 进行了验证实验来评估10bit水平条纹上带状伪影的可见性,在HDR 显示器上显示相邻区域变化一个量化水平的测试图。实验结果表明针对这类测试图,HLG 的性能表现略低于PQ,但在实际正常观看的画面中是看不到任何亮度色阶(banding)的。

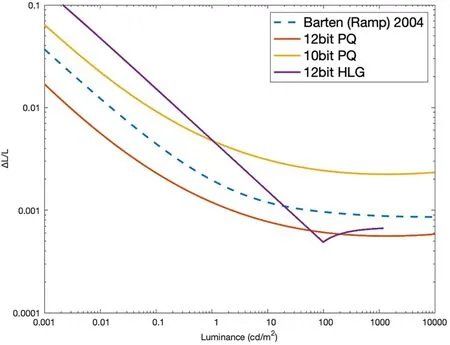
图8 10bit PQ、12bit PQ 和12bit HLG 对比

3 HDR传递函数分析

随着制造材料和生产工艺的进步,支持高动态范围(HDR)内容的显示技术已经成为了行业发展的新趋势,行业内对相关HDR 制作提出了一些标准要求。2018年ITU 发布了ITU-R BT.2100 《用于制作和国际节目交换的高动态范围电视图像参数值》,定义了HDR 视频标准,其中包含了两个光传递函数Hybrid Log Gamma (HLG)和Perceptual Quantization (PQ)。在电影工业领域中,DCI对放映显示端的EOTF 有着明确的标准,SMPTE 于2006年将DCI制定的数字电影发行放映母版标准(D-Cinema Distribution Master)采纳为SMPTE ST 428 《数字电影发行母版》。在SMPTE ST 428-1《数字电影发行母版——图像特征》中规定,DCDM 的EOTF 为Gamma 2.6 函数,像素为位深12 位,XYZ编码。随着显示设备显示能力的提高,DCI 2018年发布了 《数字电影直视型显示设备补充草案》《数字电影高动态范围补充规定草案》,前者建议EOTF 为Gamma 2.6 或PQ,后者建议EOTF采用PQ。

PQ 和HLG 都是HDR 显示器的传递函数标准,目前所有的HDR 设备都至少支持它们中的一种,且已有PQ 与HLG 相互转换的解决方案,转换后的画面以相同的亮度显示是无差异的。PQ 函数使用绝对亮度再现被摄景物,将10bit/12bit码值映射到0～10000cd/m,根据人眼视觉系统对亮度的感知对比度来最大限度地利用编码空间对数字信号进行量化,但这并不是最优解决方案,因为:

(1)计算CSF所用的测试图案都是由均匀背景和规律的光栅合成,这种情况下计算的阈值可能比普通自然图像要小得多,在普通画面中,背景和周围环境会产生一种叫“对比度掩蔽 (contrast masking)”的现象,使亮度波动的可见性降低。因此对于常规HDR 内容的编码来说,PQ 可能并没发挥出HDR 的所有潜力。观看常规画面时观众的对比敏感度可能高于PQ 理论值,其他曲线就能用更少的位深产生相同的画面质量。

(2)考虑到环境光对人眼亮度感知的影响,Barten给模型增加了一个环境光的校正因子,若环境光与测试图案的平均亮度差异很大时,校正因子会使CSF变小,这一影响因素PQ 并未考虑。值得注意的是,校正因子得出的实验前提是基于4度视角和较高空间频率的光栅,这样的实验参数设计较为严苛,与实际应用场景出入较大,因此关于更大视角下的环境光对人眼对比敏感度影响仍需后续的进一步研究。

(3)PQ 与HLG 的适用场景不同。开发PQ 的杜比公司主要专注于电影院,影院中用户的观看条件可以很好地控制,例如正常电影的显示亮度控制为48cd/m,环境中的光干扰可以尽量保持最低,尽管杜比影院的显示亮度大约为75～106cd/m,但也低于大多数电视的观看亮度。PQ 是一种基于显示器绝对亮度水平的方法,视频信号将各个数字量化编码转换为绝对亮度值,在峰值亮度有一定标准的电影行业,PQ 的显示质量较高,但将其应用在电视系统中时,如果不进行任何调整,超过电视峰值亮度的部分会被裁减。如图9所示,我们实际测量了两款不同的监视器,监视器1达到180nit左右和监视器2达到100nit左右后,码值继续增加,亮度不会再变大(监视器2在达到峰值亮度后不稳定,呈现出波浪形曲线)。

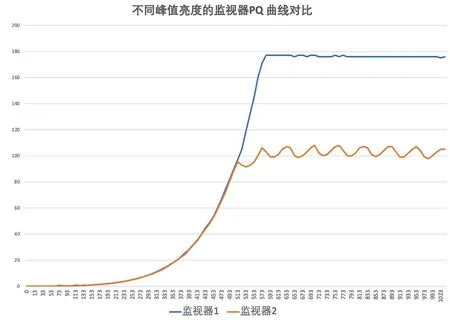
图9 10bit下两款不同监视器的PQ 曲线

与电影不同,电视的观看条件非常多样,包括屏幕尺寸、屏幕亮度和环境光等,使得调整电视的OOTF非常重要。虽然PQ 可以通过调整元数据进行修正,但实际效果仍不如本就更适用于电视系统的HLG。HLG 系统由BBC 和NHK 联合开发,这两个组织专注于电视,会根据显示器的峰值亮度改变函数中的γ (system gamma):

其中L是显示器峰值亮度。图10是两款不同监视器的PQ 和HLG 曲线对比,在不同峰值亮度下,PQ 编码显示绝对亮度,HLG 编码显示相对亮度。HLG OETF 类似于SDR TV 的OETF,并且不依赖于元数据,不同显示器之间的图像一致性更高,每个HLG 系统编码的HDR 视频信号都会自动向后兼容SDR 电视,该系统由电视工程师设计,可以满足多显示平台上电视的特殊要求。

图10 不同峰值亮度下的PQ 和HLG 曲线对比

(4)12bit Gamma2.6的优势。我们已经知道在暗观影环境下,12bit的PQ 在允许的编码范围内都不会出现亮度阶梯现象。在不同显示绝对亮度下,将PQ、HLG 和Gamma2.6相邻码值间的对比敏感度与barten曲线作比较发现,当显示的绝对亮度为200cd/m时,12bit的PQ 和Gamma 2.6都有较好的亮度量化效果,显示亮度增大到500cd/m时,12bit的Gamma 2.6和HLG 在画面暗部区域都可能会出现亮度阶梯现象。

4 结语

本文从人眼视觉系统对亮度感知的心理物理学研究入手,简要梳理了亮度感知和视觉灵敏度的研究发展历程,并分别列举其在影视领域的应用。

人眼亮度感知模型在数字影像的获取和制作方面运用已有很多年了,摄像机内部的OETF和显示端EOTF设计离不开人眼视觉感知曲线的研究。随着高动态范围影像的发展,主流HDR 格式如Dolby Vision、HDR10、HLG 和HDR10+,使用的传递函数标准不外乎PQ 和HLG 两种。在电视领域中,观看环境较为复杂,充斥着各种家庭物品的漫反射光,环境光对人眼的影响不容忽视;在电影行业,伴随着高技术格式影像的发展和画面质量的提升,自发光显示设备的运用,画面亮度越来越高,暗观影环境似乎会与人眼偏好发生冲突,这也引发了我们的思考,是否应该将环境光因素考虑进去,对传递函数做出一些相应的修改,这都需要进一步讨论。笔者相信,随着HDR 显示内容的发展,未来影院势必会在观影方式和环境上进行革新,传递函数也势必需要做出改进。❖