基于小波包散布熵与Meanshift概率密度估计的轴承故障识别方法研究
张雄 张逸轩 张明 万书亭 何玉灵 豆龙江


摘 要:為提升轴承故障特征提取精度和运行状态评估准确性,提出一种基于小波包散布熵与Meanshift概率密度估计的诊断方法. 首先,采用小波包变换对轴承振动信号数据进行升维,通过计算每个子带的散布熵构建特征矩阵;然后,利用PCA对多维矩阵进行可视化降维,采用Meanshift无参估计得到训练样本的概率密度最大位置作为聚类中心;最后,通过计算测试样本散布熵坐标与各聚类中心的欧式距离判定测试样本类别归属. 采用CWRU和QPZZ-II轴承实验台不同故障类型和故障程度样本数据对所提方法进行验证,结果表明,得益于小波包完备的理论模型和信号频带分解稀疏性,结合散布熵指标对数据样本良好的鲁棒性,所构造的特征矩阵具有较好的类内聚集性和较大的类间距离,同时,Meanshift以概率密度最大化为目标自适应迭代聚类中心和隶属度,可以有效实现对不同数据样本的分类识别.
关键词:滚动轴承;小波包散布熵;Meanshift概率密度估计;故障诊断
中图分类号:TH212;TH213.3 文献标志码:A
Research on Bearing Fault Identification Method Based on Wavelet
Packet Dispersion Entropy and Meanshift Probability Density Estimation
ZHANG Xiong1,2,ZHANG Yixuan1,ZHANG Ming1,
WAN Shuting1,2,HE Yuling1,2,DOU Longjiang1,2
(1. Hebei Key Laboratory of Electric Machinery Health Maintenance & Failure Prevention,Baoding 071003,China;
2. Department of Mechanical Engineering,North China Electric Power University,Baoding 071003 ,China)
Abstract:In order to improve the accuracy of bearing fault feature extraction and operation condition evaluation,a diagnosis method based on wavelet packet dispersion entropy and Meanshift probability density estimation is proposed. Firstly,wavelet packet transform is used to increase the dimension of bearing vibration signal data,and the dispersion entropy (DE) of each sub-band is calculated to construct the characteristic matrix. Then,PCA is used to reduce the dimension of multi-dimensional matrix visually. Meanshift nonparametric estimation is used to obtain the maximum probability density position of training samples as the clustering center. Finally,the Euclidean distance between the test sample distribution entropy coordinates and each cluster center is calculated to determine the test sample category. The experimental data of CWRU and QPZZ-II are used to verify the effectiveness of the proposed method for identifying different fault types and fault degrees. Due to the complete theoretical model of wavelet packet and the ability of signal band decomposition sparsity,combined with the good robustness of the DE index,the constructed feature matrix has good aggregation and large inter-class distance. At the same time,Meanshift aims at maximizing probability density,and can effectively classify different data samples by adaptive iterative clustering center and membership.
Key words:rolling bearing;wavelet packet dispersion entropy;Meanshift probability density estimation;fault diagnosis
滚动轴承是旋转机械中最常见、故障率最高的零部件之一,它的运行状态关系到整个机械设备的可靠性和安全性,因此,轴承故障诊断方法是近年来工程测试和信号处理领域的热点[1-3]. 振动信号中含有大量的轴承周期性冲击信息,在轴承故障诊断中有着广泛的应用[3-6].
轴承故障诊断一般分为两步. 第一步是故障特征的提取过程. 这一过程的核心是如何准确地抑制振动信号中的干扰信息,准确地提取故障特征元素. 在这一过程中,通常采用小波变换(Wavelet Transform[7]、小波包变换(Wavelet Packet Transform)[8]、经验小波变换(Empirical Wavelet Transform)[9]、经验模态分解(Empirical Mode Decomposition)[10]、集成经验模态分解(Ensemble Empirical Mode Decomposition)[11]、局部均值分解(Local Mean Decomposition)[12]等处理手段对信号进行滤波和增维处理,目的是提取能更有效反映轴承故障信息的模态分量. 通过对分解后和滤波后的分量的动态特性进行统计学计算,构造出能够反映轴承振动信号的特征矩阵. 其中信息熵、排列熵、模糊熵等动力学指标常被用来反映信号的瞬态特征. 陈法法等[13]提出一种基于信息熵与优化最小二乘支持向量机的轴承性能退化趋势模糊粒子预测方法,用于提升轴承性能退化指标预测精度. Zhang等[14]通过计算局部迭代分解滤波后固有模态分量的多尺度排列熵,构造归一化特征向量,对不同工况条件下的轴承故障进行识别. 郑近德等[15]采用复合多尺度模糊熵和迭代拉普拉斯得分对变分模态分解升维后的信号进行敏感特征选择,以支持向量机对不同故障类型进行划分. 第二步是利用机器学习方法将特征集作为训练样本和测试样本进行模式识别. 该部分的核心问题包括聚类、分类、回归和降维. Li等[16]对比分析了模糊C均值(Fuzzy C-Means,FCM)、Gustafson-Kessel算法、FN-DBSCAN和FCMFP算法各自特点. Yu等[17]利用Gath-Geva(GG)聚类对故障特征进行分类,得到各轴承状态的聚类中心和隶属度矩阵,进行模式识别.
构造能够充分反映信号样本属性且具有良好类内聚集性的特征矩阵,并寻求具有自适应能力和边界特征的样本分类方法是模式识别领域的核心问题. 本文提出了一种基于小波包散布熵与Meanshift概率密度估计轴承故障特征矩阵构造方法,通过计算样本小波包各子带的散布熵值,构建特征矩阵;进而利用PCA对特征矩阵进行可视化降维,选取贡献度最高的两个主成分;最后采用Meanshift概率密度估计聚类中心位置. 通过实验数据分析,验证了该方法能有效识别不同类型的故障和不同程度的故障.
1 基本理论
1.1 小波包散布熵
小波包变换能同时连续分解信号的高频分量和低频分量,并能自适应地确定不同频段的分辨率,大大提高了信号的时频局部分析能力,得到了广泛的应用. 小波包变换过程可用式(1)表示.
式中:xi,j表示第i层的第j子带信号(其中,i是分解层数,j是对应层的信号数);K为序列长度;Ln和Gn分别是小波包的低通滤波器和高通滤波器.
为了解决样本熵计算时间长、实时性差、排列熵不考虑平均振幅与振幅之差等问题,Rostaghi等[18]提出了一种新的时间序列不规则性度量指标,称为散布熵(Dispersion Entropy,DE). 与样本熵和排列熵(Permutation Entropy,PE)类似,散布熵也是一种表征时间序列不规则性的方法. 散布熵值越大,不规则度越高;散布熵值越小,不规则度越低.
对于长度为N的时间序列x = {xj,j = 1,2,…,N},散布熵的计算步骤如下:
1)通过正态分布函数用于将时间序列映射到y = {yj,j = 1,2,…,N}.
式中:μ和σ2分别表示序列的期望和方差.
2)通过线性变换将y映射到[1,2,…,c]范围.
zcj = R(c·yj + 0.5) (3)
式中:c为类别个数;R为取整函数.
3)计算嵌入向量:
zm,ci =(zci,zc i+d,…,zc i+(m-1)d),i = 1,2,…,N-(m-1)d
(4)
式中:m和d表示嵌入维数和时延.
4)计算散布模式π v0 v1…vm - 1(v=1,2,…,c),如果zc i+d=v1,…,zc i+(m-1)d=vm - 1,则π v0 v1…vm - 1为zm,ci 对应散布模式.
5)计算散布模式π v0 v1…vm - 1的概率:
式中:Number(π v0 v1…vm - 1)表示zm,ci 在π v0 v1…vm - 1中的映射个数.
6)类比香农熵定义,将原信号的散布熵定义为:
当所有散布模式具有相同的概率(如噪声信号)时,散布熵取最大值lncm. 相反,當只有一个p(π v0 v1…vm - 1)值不等于零时(如周期信号),则表示时间序列是完全规则或可预测的数据,散布熵取最小值.
1.2 Meanshift概率密度估计
Meanshift聚类算法是一种无参数的聚类算法,能够在根据样本点计算数据概率密度分布区间. 该算法已成功应用于图像平滑、图像分割和运动目标跟踪等领域.
设Rd为d维空间,x = {xi}(i = 1,2,…,n)为离散数据集合. Meanshift可以定义为:
(7)
式中:Sh(x) = { y:(y - x)T(y - x) ≤ h2 }为球体区域;h为半径.
向量Mh(x)对数据的概率密度梯度具有指向性. 由于不同距离的点具有不同的权重系数,引入核函数K(x),概率密度函数f(x)表示为:
(8)
核函数定义为:
K(x) = ok,d k(‖x‖2) (9)
式中:o为正则化系数,用来保证k(x)dx = 1.
通过求偏导得到概率密度函数f(x)极值点.
式中:g(x)=-k′(x),相应的核函数为G(x)=og,dg(||x||2). 公式前半部分是以G(x)为核函數的概率密度估计的概率密度估计,后半部分为Meanshift所指向的最大概率密度梯度的方向,可以表示为
Meanshift算法本质上是一种自适应递增迭代搜索数据分布概率密度分布梯度峰值的运算. 迭代次数为t,搜索窗口(空间)为r,给定任意初始点x. 迭代过程可以表述如下:
1)初始化t,r,设定阈值σ;
2)计算第t次迭代的概率密度梯度mh(xt);
3)更新搜索空间r,xt + 1 = xt + mh(xt);
4)重复步骤2和步骤3,直至mh(xt)≤σ.
采用仿真数据对上述过程进行说明. 给定一组以一定概率分布在二维空间中的数据点. 设定Meanshift算法参数为r = 0.5,σ = 1 × 10-4. 迭代过程如图1所示,对所设定的高维球区域内中心位置到离散数据点的向量进行加权处理,合成迭代向量梯度方向(类似于力的合成),然后,更新搜索窗口位置. Meanshift算法在不预先设定分类数的情况下,可以自适应地沿着概率密度梯度方向迭代,并最终找到聚类中心的位置.
1.3 故障特征表征及模式识别过程
本文提出的轴承故障诊断方法流程如图2所示,具体步骤如下.
1)构建特征矩阵. 选取训练样本形成信号集x = (x1,x2,…,xm),对原始信号集中的各个元素进行小波包分解,计算每个小波包子带的散布熵构建特征矩阵WP = (WPix1,WPix2,…,WPixn) i = 1,2,3,4.
2)采用主成分分析法对特征矩阵进行降维. 将特征矩阵投影到二维空间,选择贡献率最高的两个主成分构造二维特征矩阵(选择两个主成分(Principal Component,PC)可以显示为二维图,三个PC可以显示为三维图,本文数据特征样本以二维平面图的形式显示,选择贡献率最高的前两个PC分量构造特征矩阵).
WP = (WPix1,WPix2,…,WPixn)Λ=(PC1xn,PC2xn)
3)建立了估计模型. 设定Meanshift参数(本文搜索半径r的取值原则为在保障聚类种数的前提下,选择尽可能小的窗口半径),对主成分空间坐标点进行概率密度估计,得到聚类类别和聚类中心.
4)对测试样本进行估计. 对测试样本重复上述步骤1和步骤2,得到主成分特征矩阵,并计算其与训练样本的聚类中心的欧式距离,得到相应的隶属关系.
2 实测信号分析
为了验证该方法对轴承不同故障类型和故障程度诊断的有效性,分别采用CWRU实验室开源数据和QPZZ-II旋转机械故障模拟实验台数据进行分析.
2.1 CWRU滚动轴承实验数据分析(不同故障程度)
故障源数据为驱动端SKF6205轴承经电火花加工在内圈生成的四类故障程度样本,故障尺寸分别为0.007英寸,0.014英寸,0.021英寸和0.028英寸(本文选用数据为美国凯斯西储大学实验台数据,原数据说明中使用单位为英寸,故本文使用单位为英寸.转换为国际单位后,四类样本故障尺寸分别是0.017 78 cm,0.035 56 cm,0.053 34 cm和0.071 12 cm). 电机转速为1 750 r/min,采样频率为12 kHz,轴承实验台模型如图3所示.
对四类不同故障程度的振动信号数据各取一组样本,其时域波形如图4所示.
验证散布熵相较于排列熵的稳定性以及对于不同故障程度具有较好的区分度. 对四类不同故障程度的振动信号划分成不同数据长度构造数据节点,节点1数据长度为512,节点2数据长度为1 024(512×2),节点3数据长度为2 048(512×4),节点4对应数据长度为3 072(512×6),以此类推. 分别计算四类故障程度振动信号10个节点数据的散布熵,结果如图5所示. 可以看出,不同故障程度下散布熵随数据点长度增长的走势大体相近且变化平缓,四种故障程度在各节点具有较好的区分度.
计算上述各节点的排列熵作为对比,结果如图6所示,可以看出,不同故障程度下排列熵随数据长度增长的走势振荡明显,且存在交叉,说明数据长度的选择在较大程度上影响类间区分度.
对四类不同故障程度振动信号各取40组分析样本,其中20组为训练样本,20组为测试样本,采用本文所提故障识别方法进行处理. 首先利用小波包分解对训练样本数据进行升维处理,然后计算每个样本小波包各子带的散布熵值,构建特征矩阵,进而利用PCA对特征矩阵进行可视化降维,选取贡献度最高的两个主成分,最后采用Meanshift概率密度估计聚类中心位置,结果如图7所示.
对20组测试样本进行分析,采用同样的方法计算小波包散布熵构造特征矩阵,并通过PCA进行可视化降维,然后计算测试样本点与上述聚类中心的归一化欧氏距离,结果如图8所示. 归一化欧氏距离越小,说明样本与该聚类中心的隶属度越高,可以看出,测试样本被較清晰的划分到四类故障程度类别中.
采用EEMD排列熵构造特征矩阵进行对比分析,通过PCA可视化降维和Meanshift概率密度估计后的训练样本分布和聚类中心位置如图9所示.可以看出,数据分布的类间距较小,类内聚集性较差. 测试样本与各聚类中心的归一化欧氏距离如图10所示,可以看出,测试样本1和测试样本2出现较为严重的混叠,难以明确其隶属关系.
2.2 QPZZ-II旋转机械故障模拟实验台数据分析
(不同故障类型)
为进一步验证所提方法的有效性,采用QPZZ-II轴承故障模拟实验台(电机功率0.55 kW,调速范围75~1 450 r/min)进行数据分析,故障轴承型号6205E(利用线切割分别在内圈、外圈及滚动体植入故障),轴承座位置水平方向和垂直方向布置振动加速度传感器(型号:东华1A116E,量程:50 g),测试系统采用DH5922N型动态信号采集分析仪(16通道/256 kHz),采样频率为12 800 Hz,实验台结构图如图11所示. 对三类不同故障类型的振动信号数据各取一组样本,其时域波形如图12所示.
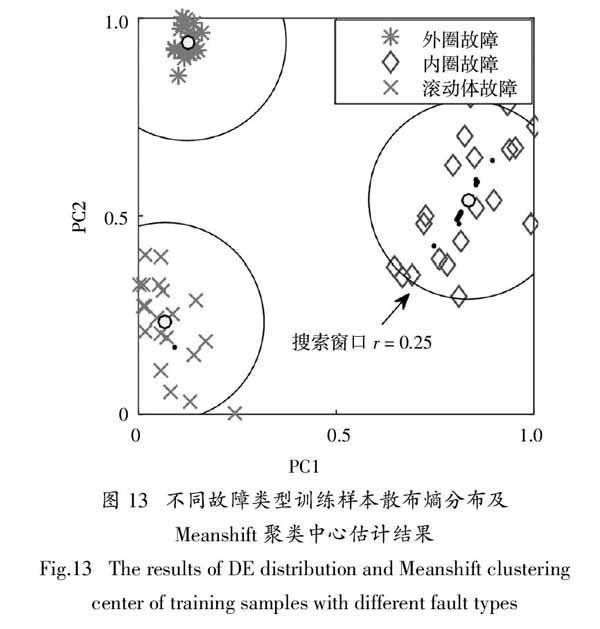
对三类不同故障类型振动信号各取40组分析样本,其中20组为训练样本,20组为测试样本,采用本文所提故障识别方法进行处理. 对20组训练样本构造小波包散布熵特征矩阵,利用PCA进行可视化降维,并用Meanshift概率密度估计聚类中心,结果如图13所示. 对20组测试样本进行分析,计算测试样本点与上述聚类中心的归一化欧氏距离,结果如图14所示. 可以看出,测试样本被较清晰的划分到三类故障程度类别中. 采用EEMD排列熵构造特征矩阵进行对比分析,训练样本分布和聚类中心位置如图15所示,测试样本与各聚类中心的归一化欧氏距离如图16所示,可以看出,测试样本1和测试样本2出现较为严重的混叠.
3 结 论
本文针对轴承故障模式识别领域的两类典型问题(不同故障类型和不同故障程度数据样本识别)展开研究,提出一种基于小波包散布熵和Meanshift概率密度估计的轴承故障模式识别方法,通过CWRU和QPZZ-II实验台数据分析验证了所构造的小波包散布熵特征矩阵能够充分反映信号样本属性且具有较好类内聚集性,同时Meanshift无参概率密度估计具有良好的聚类边界和数据样本模式识别能力. 具体而言:
1)散布熵随数据点长度增长的走势相较于排列熵变化平缓,各节点具有较好的区分度,说明散布熵对截取的不同长度信号样本具有更好的稳定性和适应性.
2)训练样本的小波包散布熵经PCA降维后相较于同样处理的EEMD排列熵具有更稳定的聚类区域以及更大的类间距离.
3)Meanshift无参概率密度估计能够通过迭代准确识别样本特征的聚类中心,通过计算测试样本散布熵坐标与各聚类中心的欧氏距离可以实现对测试样本隶属关系的判别.
参考文献
[1] 邵海东,张笑阳,程军圣,等. 基于提升深度迁移自动编码器的轴承智能故障诊断[J]. 机械工程学报,2020,56(9):84—90.
SHAO H D,ZHANG X Y,CHENG J S,et al. Intelligent fault diagnosis of bearing using enhanced deep transfer auto-encoder[J]. Journal of Mechanical Engineering,2020,56(9):84—90. (In Chinese)
[2] 杨蕊,李宏坤,王朝阁,等. 利用FCKT以及深度自编码神经网络的滚动轴承故障智能诊断[J]. 机械工程学报,2019,55(7):65—72.
YANG R,LI H K,WANG C G,et al. Intelligent fault detection for rolling element bearing based on FCKT and deep auto-coding neural network[J]. Journal of Mechanical Engineering,2019,55(7):65—72. (In Chinese)
[3] 陈仁祥,黄鑫,杨黎霞,等. 基于卷积神经网络和离散小波变换的滚动轴承故障诊断[J]. 振动工程学报,2018,31(5):883—891.
CHEN R X,HUANG X,YANG L X,et al. Rolling bearing fault identification based on convolution neural network and discrete wavelet transform[J]. Journal of Vibration Engineering,2018,31(5):883—891. (In Chinese)
[4] 罗洁思,张绍辉,李叶妮. 多分辨奇异值分解在滚动轴承振动信号解调分析中的应用[J]. 振动工程学报,2019,32(6):1114—1120.
LUO J S,ZHANG S H,LI Y N. Application of multi-resolution singular value decomposition in vibration signal demodulation analysis of rolling bearing[J]. Journal of Vibration Engineering,2019,32(6):1114—1120. (In Chinese)
[5] 彭延峰,刘贞涛,程军圣,等. 基于初值优化的自适应最稀疏时频分析方法[J]. 湖南大学学报(自然科学版),2017,44(8):50—56.
PENG Y F,LIU Z T,CHENG J S,et al. Adaptive and sparsest time-frequency analysis method based on initial value optimization[J]. Journal of Hunan University (Natural Sciences),2017,44(8):50—56. (In Chinese)
[6] 余發军,周凤星. 基于可调Q因子小波变换和谱峭度的轴承早期故障诊断方法[J]. 中南大学学报(自然科学版),2015,46(11):4122—4128.
YU F J,ZHOU F X. Bearing early faults diagnosis based on tunable Q-factor wavelet transform and spectral kurtosis[J]. Journal of Central South University (Science and Technology),2015,46(11):4122—4128. (In Chinese)
[7] 赵靖,廖英英,杨绍普,等. 基于无迹卡尔曼滤波的动态贝叶斯小波变换在轴承故障诊断中的应用[J]. 振动与冲击,2020,39(11):53—62.
ZHAO J,LIAO Y Y,YANG S P,et al. An extension of unscented Kalman filter to dynamic Bayesian wavelet transform in fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock,2020,39(11):53—62. (In Chinese)
[8] 王丽华,陶润喆,张永宏,等. 基于CEEMD-WPT的滚动轴承特征提取算法[J]. 振动·测试与诊断,2017,37(1):181—188.
WANG L H,TAO R Z,ZHANG Y H,et al. Feature extraction of rolling bearing based on CEEMD-WPT[J]. Journal of Vibration,Measurement & Diagnosis,2017,37(1):181—188. (In Chinese)
[9] 杜小磊,陈志刚,王衍学,等. 基于IEWT和IFractalNet的滚动轴承故障诊断[J]. 振动与冲击,2020,39(24):134—142.
DU X L,CHEN Z G,WANG Y X,et al. Fault diagnosis of rolling bearings based on improved empirical wavelet transform and IFractalNet [J]. Journal of Vibration and Shock,2020,39(24):134—142. (In Chinese)
[10] 张立智,徐卫晓,井陆阳,等. 基于EMD-SVD和CNN的旋转机械故障诊断[J]. 振动·测试与诊断,2020,40(6):1063—1070.
ZHANG L Z,XU W X,JING L Y,et al. Fault diagnosis of rotating machinery based on EMD-SVD and CNN[J]. Journal of Vibration,Measurement & Diagnosis,2020,40(6):1063—1070. (In Chinese)
[11] 李华,刘韬,伍星,等. EEMD和优化的频带熵应用于轴承故障特征提取[J]. 振动工程学报,2020,33(2):414—423.
LI H,LIU T,WU X,et al. EEMD and optimized frequency band entropy for fault feature extraction of bearings[J]. Journal of Vibration Engineering,2020,33(2):414—423. (In Chinese)
[12] 张坤,马朝永,胥永刚,等. 快速自适应局部均值分解及轴承故障诊断应用[J]. 振动工程学报,2020,33(1):206—212.
ZHANG K,MA C Y,XU Y G,et al. Fast and adaptive local mean decomposition method and its application in rolling bearing fault diagnosis[J]. Journal of Vibration Engineering,2020,33(1):206—212. (In Chinese)
[13] 陈法法,杨勇,马婧华,等. 信息熵与优化LS-SVM的轴承性能退化模糊粒化预测[J]. 仪器仪表学报,2016,37(4):779—787.
CHEN F F,YANG Y,MA J H,et al. Fuzzy granulation prediction for bearing performance degradation based on information entropy and optimized LS-SVM[J]. Chinese Journal of Scientific Instrument,2016,37(4):779—787. (In Chinese)
[14] ZHANG J B,ZHAO Y Q,LIU M,et al. Bearings fault diagnosis based on adaptive local iterative filtering-multiscale permutation entropy and multinomial logistic model with group-lasso[J]. Advances in Mechanical Engineering,2019,11(3):1—13.
[15] 郑近德,姜战伟,代俊习,等. 基于VMD的自适应复合多尺度模糊熵及其在滚动轴承故障诊断中的应用[J]. 航空动力学报,2017,32(7):1683—1689.
ZHENG J D,JIANG Z W,DAI J X,et al. VMD based adaptive composite multiscale fuzzy entropy and its application to fault diagnosis of rolling bearing[J]. Journal of Aerospace Power,2017,32(7):1683—1689. (In Chinese)
[16] LI C,CERRADA M,CABRERA D,et al. A comparison of fuzzy clustering algorithms for bearing fault diagnosis[J]. Journal of Intelligent & Fuzzy Systems,2018,34(6):3565—3580.
[17] YU K,LIN T R,TAN J W. A bearing fault diagnosis technique based on singular values of EEMD spatial condition matrix and Gath-Geva clustering[J]. Applied Acoustics,2017,121:33—45.
[18] ROSTAGHI M,AZAMI H. Dispersion entropy:a measure for time-series analysis[J]. IEEE Signal Processing Letters,2016,23(5):610—614.
收稿日期:2021-03-04
基金項目:国家自然科学基金资助项目(52105098,51777075),National Natural Science Foundation of China(52105098,51777075);河北省自然科学基金资助项目(E2021502038,E2019502064),Natural Science Foundation of Hebei Province(E2021502038,E2019502064);中央高校基本科研业务费专项资金资助项目(2020MS111),The Fundamental Research Funds for the Central Universities(2020MS111)
作者简介:张雄(1990—),男,河北保定人,华北电力大学博士,硕士生导师
通信联系人,E-mail:zxncepu@163.com

