一类常微分方程和偏微分方程的级联系统的边界控制

雷 嫄，白艺昕，谢成康

西南大学 数学与统计学院，重庆 400715

本文考虑如下控制系统

(1)

其中：X(t)∈Rn表示流体的温度、湿度、密度等物理参数，矩阵A，B∈Rn×n且(A，B)能稳，U(x，t)∈Rn为状态变量，矩阵Λ∈Rn×n，C(t)∈Rn是控制输入，0表示零矩阵或零向量．

1 控制器设计

(2)

这里的核函数Φ(x，y)∈Rn×n和矩阵函数Ψ(x)∈Rn×n待定．该变换将系统(1)转换为一个指数稳定的目标系统，从而设计出控制律，那么闭环系统的稳定性就可以通过该变换及其逆变换建立起来．选定的目标系统如下

(3)

其中选定K∈Rn×n使得A+BK是Hurwitz矩阵，为了满足方程组(3)第4式，取控制律为

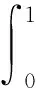
(4)

取核函数Φ(x，y)和矩阵函数Ψ(x)满足如下方程组

(5)

通过方程组(2)第2式以及方程组(3)第3式，可以得到矩阵函数Ψ(x)的一个边界条件为

Ψ(0)=0

(6)

此外，状态X(t)满足方程组(1)第1式和方程组(3)第1式，

(KX(t)+Wx(0，t)-Ux(0，t))=0

(7)

可取如下条件成立

Ψ′(0)=K

(8)

首先，根据矩阵函数方程组(5)第4式及其边界条件(6)和(8)，本文得到矩阵方程的一个级数解为

(9)

其次由方程组(5)及式(9)，可将核函数满足的边界条件转化为

Φxx(x，y)-Φyy(x，y)=Φ(x，y)Λ

(10)

可将核函数化为积分方程，再利用逐次逼近法求得近似解，其求解过程可参考文献[15]．最后得到核函数解为

(11)

2 稳定性

首先证明目标系统(3)的稳定性．

引理1对于目标系统(3)，存在α>0，β>0，使得

(12)

即目标系统在H1范数意义下指数稳定，其中‖·‖表示欧几里得范数，‖W(t)‖H1表示W(t)的H1范数，即

证选取李雅普诺夫函数

(13)

这里的矩阵P>0是Lyapunov函数

P(A+BK)+(A+BK)TP=-I

(14)

的解，其中I表示n阶单位阵，a>0是需要被确定的参数．对Lyapunov函数(13)两边关于t求导，由于W满足方程组(3)，所以有

通过分部积分，由边界条件方程组(3)第3式和第(4)式，有

因为W满足方程组(3)第1式，所以V(t)满足

(15)

由Agmon不等式、Cauchy-Schwartz不等式和Young不等式

取

a=2‖B‖2‖P‖2+2

再由Poincare不等式及

Wx(1，t)=0，W(0，t)=0

得

(16)

又因为

λmin(P)‖X(t)‖2≤X(t)TPX(t)≤λmax(P)‖X(t)‖2

其中λmax(P)是P的最大特征值，那么，由(13)式可得

(17)

其中

就可以得到

V(t)≤V(0)e-βt

(18)

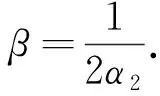
证明变换(2)可逆，需找到它的逆变换，故假设逆变换具有如下形式

(19)

按照求解核函数Φ(x，y)，Ψ(x)的思路和方法，能得到

(20)

(21)

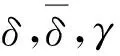
(22)

(23)

证从变换(2)第2式及范数的性质，可得

(24)

接下来需要对第2项和第3项进行估计．首先

根据Holder不等式

(25)

(26)

其中

同理由逆变换可得

(27)

其中

因此，由式(24)，(25)，(26)及(27)，当取

δ=1+δ1+δ2

时式(22)成立．同理可证式(23)成立．

根据引理1和引理2可以得到如下定理．

定理1设Φ(1，y)和Ψ(1)是方程(11)及(9)的解．考虑系统(1)，控制律为(4)，则存在常数σ使得

(28)

即闭环系统在上述范数下是指数稳定的．