教材中价层电子对互斥理论的问题探讨

李保山

北京化工大学化学学院，北京 100029

N. V. Sidgwick等把原子结构中的保利不相容原理，即“自旋相同的电子必须远离”这一原则推广至分子结构中，提出在一些简单的共价分子(ABn)中，中心原子A的价层轨道电子对是环绕中心原子A排列成对称的几何结构的，这种结构使得各电子对相互远离，电子对之间的净斥力达到最小，分子体系的能量达到最低。据此，可以推测这些简单分子中中心原子价电子对的几何分布情况，进一步推测分子的几何构型。这种定性解释分子几何构型的近似方法称之为“价层电子对互斥理论(Valence Shell Electron Pair Repulsion Theory)”，简称VSEPR法。

VSEPR法比较简单，易于理解和掌握[1–16]。对于绝大多数ABn型的简单共价分子、离子的几何构型均可以准确地推测，可以认为这一方法在认识这些简单共价分子、离子的几何构型方面上升到了比杂化轨道理论更科学的层面，因为杂化轨道理论只能解释已知几何构型的简单共价分子或离子的几何结构，而不能推测其几何结构。因此，VSEPR法得到了广泛的运用。

但在目前的教材中对于VSEPR法的理解尚不统一，其应用方法存在着多个版本，有些教材对这一理论应用的描述难以理解，有的添加了更多的假定成分，易于导致初学者产生疑惑。

本文对目前国内外常见的几种教材对这一理论的应用过程进行对比分析，旨在形成对这一化学基本理论的共识。

1 VSEPR法理论要点

在利用VSEPR法推测简单分子(或离子)中中心原子的价电子几何分布情况时，可以将这些分子(或离子)记为ABnEm。其中A为中心原子，B为配位原子，E为孤对电子，n和m分别是成键电子对数和孤电子对数。该理论的基本要点[1–10]：

1) 中心原子形成的共价键数与原子的价层轨道数及价电子数有关，多数原子在形成分子时已经成对的电子可能会被激发到能量较高的p轨道或d轨道上，从而形成更多的价层轨道，所以中心原子成键时可以不受八隅律限制，其价层电子对数可能大于4 (即n+m大于4)，甚至可达12 (表1)。

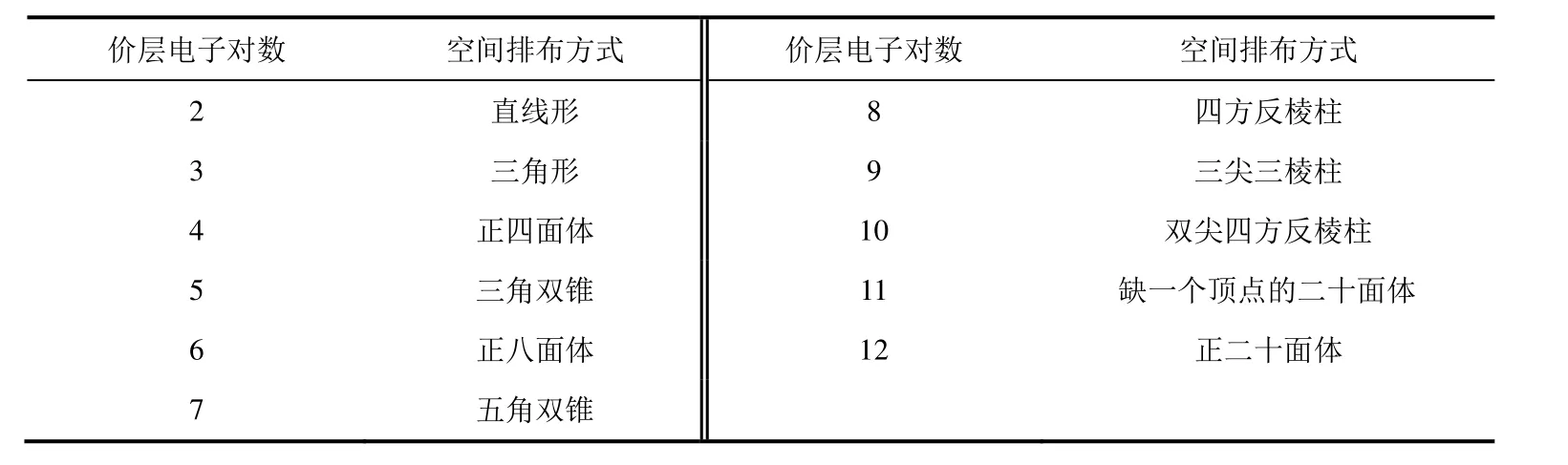
表1 价层电子对的高对称性空间排布方式

2) 中心原子A的价电子层(即最外层)电子对彼此排斥，尽可能地远离，最终形成高度对称的空间排布结构。

价层电子对具有两种类型：成键的σ键电子对(骨架电子对，用BP表示)和没成键的孤电子对(用LP表示)。分子中除了电子对间的排斥力之外，所有电子对还都受A、B原子核的吸引力，当这两种力达到平衡时，就决定了价层电子对的位置，价层电子对在中心原子周围的分布情况与价层电子对数目有关。常见的电子对高对称性空间排布方式见表1。

3) 价层电子对之间排斥力的大小取决于电子对在中心原子周围分布的夹角和电子对的类型。排斥力大小顺序为：

① LP-LP > LP-BP > BP-BP。

② 三键>双键>单键。

可见价层电子对间夹角的大小顺序为：LP-LP > LP-BP > BP-BP。

4) 分子或离子的几何结构主要取决于中心原子A与配位原子B之间形成的σ键，π键对分子骨架结构的影响较小，其存在的位置对相邻的价层电子对具有较大的斥力，进而对键角产生一定的影响。

5) 配位原子的电负性也会影响键角的大小。电负性越大，σ键电子对越远离中心原子，受其他电子对的斥力就越小，进而对键角产生一定的影响。

可见，分子或离子的几何结构主要取决于中心原子价层电子对数和价层电子对的类型，π键及配位原子的电负性仅对键角产生较小的影响。因此，可以用这一理论定性地推测简单共价分子或离子的几何结构。

但目前不同教材中对这一理论的应用方法介绍不统一，主要是确定中心原子的价层电子对数方法不统一，导致教学过程中出现了一些问题。下面就目前常用的几种教材中确定中心原子的价层电子对数方法作一介绍。

2 确定中心原子价层电子对数的主要方法

2.1 根据Lewis电子式确定

这种方法是先要写出分子或离子的Lewis电子结构式，判断骨架电子对数和孤电子对数，进一步判断分子或离子的几何结构[1–4]。该方法基于八隅律，例如电子式为，中心原子S的价层有3对成键电子和一对孤电子，中心原子的价层电子对数为4。再如，要满足C、O原子的八隅结构，C与O原子之间要形成双键，所以C原子的骨架电子对数为3。同样，SO3的Lewis电子式可写为，要满足S、O原子的八隅结构，S与其中一个O原子之间要形成双键，所以S原子的骨架电子对数为3。

这种方法虽然比较直观，但方法的适应性不强[8]。

2.2 根据中心原子的族数及配位原子提供的电子数确定

国内一些教材[5–12]给出的价层电子对数VP的计算公式为：

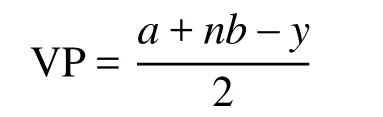
上式中a为中心原子A的价电子数，n为配位原子数，b为配位原子提供的电子总数；y为离子的电荷数(代数值)，阳离子为“+”，阴离子为“−”。若出现小数(如0.5、1.5等)，则进为整数(1或2)即可。该式的物理意义可以理解为：中心原子周围的总价层电子数等于中心原子的基态价层电子数和配位原子提供的价层电子数之和。

这些教材中认为：作为配位原子的B原子通常是氢、卤素、氧和硫。在计算配位原子提供的电子数时，氢和卤素记为“1”，氧和硫记为“0”，即认为氧和硫作为配位原子时，不提供价电子，而氧和硫作为中心原子时，价电子数记为“6”[5–8]。

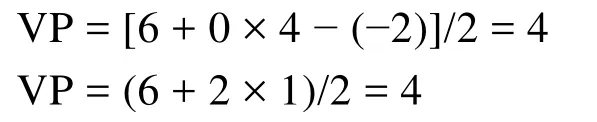
再如BrF5和XeOF4中原子Br和Xe的价层电子对数分别为：

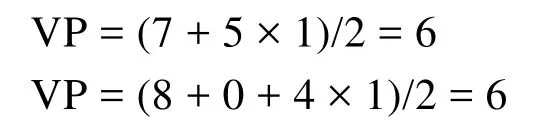
这种方法可以推测简单分子的几何结构，但这些教材[5–12]中认为：氧和硫作为配位原子时提供的电子数为0，而作为中心原子时提供的价电子数为6。这样的处理方法对于初学者而言是不易理解和接受的，因为这样的说法实际上不准确。

正确的描述应该是：“氧和硫作为端原子配位(即除中心原子外无其他原子与其键连)时不提供价电子”，而不是作为配位原子时不提供价电子。因为氧和硫为端原子时，是通过双键与中心原子配位相连的，而π键对分子骨架结构的影响较小，若氧或硫原子按提供2个价电子计算，结果中将多出π键的1对电子，为了避免这种情况，规定：氧和硫为端原子配体时不提供价电子。若氧和硫作为端基配位原子而非端原子配位时，如―OH，就不能认为O原子不提供价电子，而是提供1个价电子。

2.3 根据基态中心原子的价电子数及配位原子的未成对电子数确定

该方法给出中心原子A的价电子对数的计算公式为[13–16]：

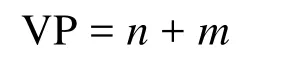
式中n和m分别为A与B之间形成的σ键数和孤电子对数，其中m的计算公式为：

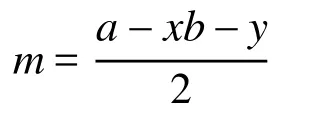
式中a为中心原子的基态价电子数，b为配位原子的未成电子数，x为配位原子数，y为离子的电荷数(代数值)。若出现小数(如0.5、1.5等)，则进为整数(1或2)即可。该式具有明确的物理意义，即孤电子对数等于中心原子基态价层电子数与配位原子和中心原子之间的成键电子数(包括σ键和π键)之差的1/2。可以理解为配位原子B的未成对电子均要与中心原子的电子配对，即B原子也要满足八隅律。

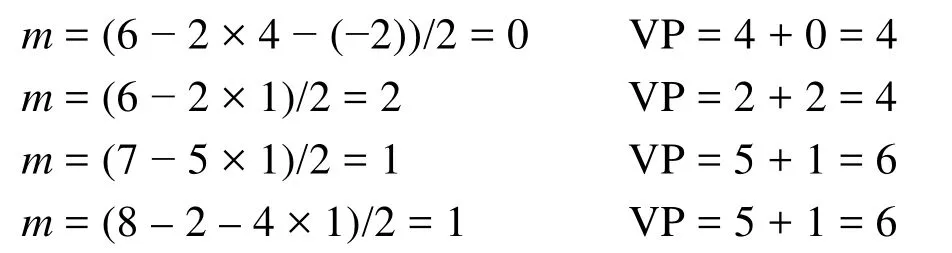
需要说明的是，配位原子的未成电子数b是指其未与中心原子成键的电子数。若配位原子为端原子，其未成对电子数等于其基态的未成对电子数；对于非端原子(即端基)配位，其未成对电子数应该减去与其他原子键连所用去的电子数，若与其他原子以单键相连则减去1，双键减去2，三键减去3。例如中的端原子O，提供的未成对电子数为2，而端基H3C―和―O―CH3中的配位原子C及O的未成对电子数均为1。这是因为端基中C的4个未成对电子中已有3个与氢原子键连，而氧的2个未成对电子中有1个与端基―O―CH3中的C键连。再如，与中心C*原子相连的1位C有3个电子已与其他原子配对，2位C有2个电子已与其他原子配对，所以1位和2位上的C提供的未成对电子数分别为1和2。

这种计算方法没有规定某原子提供的电子数是多少，比2.2节的方法易于理解和掌握。

2.4 根据相关原子的基态价层电子总数及配位原子的八隅律确定

该方法计算中心原子A的价电子对数的计算公式与2.3节方法一致[17–20]：

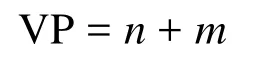
式中n和m分别为A与B之间形成的σ键数和孤电子对数，其中m的计算公式为：

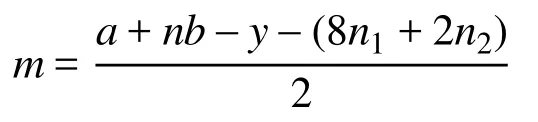
式中a为中心原子A的基态价层电子数，n为配位原子数，b为配位原子的基态价层电子数，n1和n2分别为配位的非氢原子数和氢原子数，y为离子所带电荷的代数值。这个公式的物理意义与2.3节的公式基本相同，可以理解为配位原子均形成了八隅体(氢原子除外)，中心原子周围的孤电子数等于总的价层电子数减去配位原子与中心原子的成键电子数。

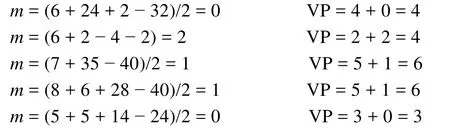
这种方法与2.3节的方法均是以基态原子的电子结构及配位原子的八隅律(氢原子除外)为基础，没有其他假定，且均可获得满意的推测结果，易于理解和掌握。相比之下，作者认为2.3节的方法更简便、易懂、易记。

3 分子或离子几何结构的推测方法步骤

价层电子对在中心原子周围的几何分布情况，就决定了分子或离子的几何构型。

对于孤电子对数等于零的情况，分子或离子的几何构型与价层电子对构型一致；而对于孤电子对数不等于零的情况，要通过不同类型的电子对之间的排斥力大小来排布配位原子的位置。

当分子中有π键存在时，π键应排在相当于孤对电子的位置。另外，π键和配位原子电负性也会使键角发生变化。

下面给出推测分子或离子几何结构的方法步骤。

第一步：确定中心原子及配位原子。

一般认为分子(或离子)中氧化数绝对值最大者为中心原子，和中心原子直接相连的其他原子为配位原子(包括端原子和端基配位原子)。也可以指定分子中的某个原子为中心原子，与其直接相连其他原子或原子团为端原子或端基。但F、H几乎均为配位原子，这是因为F的电负性最大，而氢原子只有1个单电子。

第二步：以第2.3节方法为例计算孤电子对数和VP数。

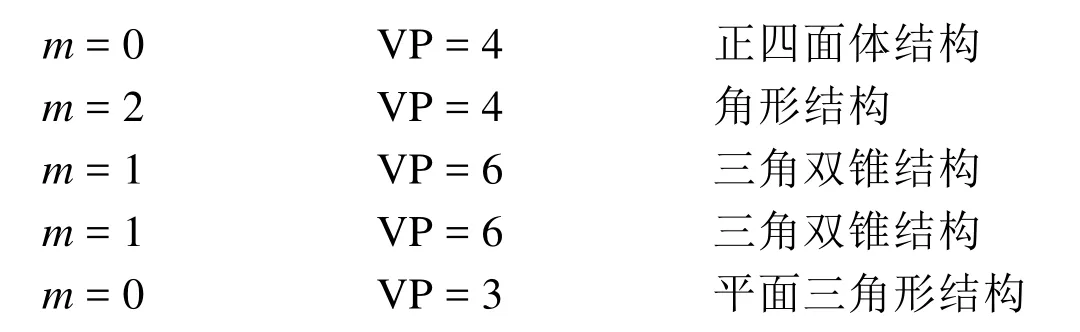
当配位原子上连接除中心原子以外的其他原子时，其未成对电子数应该减去配对其他原子的电子数，与其他原子若以单键相连则减去1，双键减去2，三键减去3。

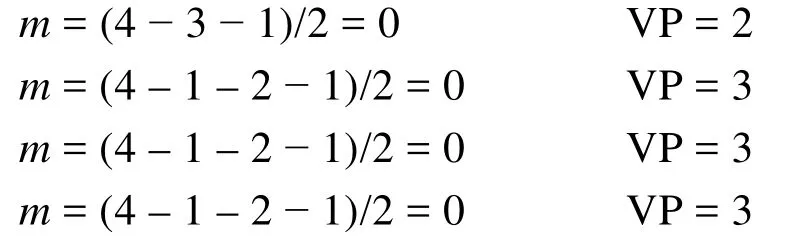
第三步：推测分子或离子的结构。

1) 孤电子对数等于零的分子或离子，其几何构型与价层电子对构型一致。但当分子中有π键存在时，π键应排在相当于孤对电子的位置。表2给出了推测这类分子结构的一些实例。

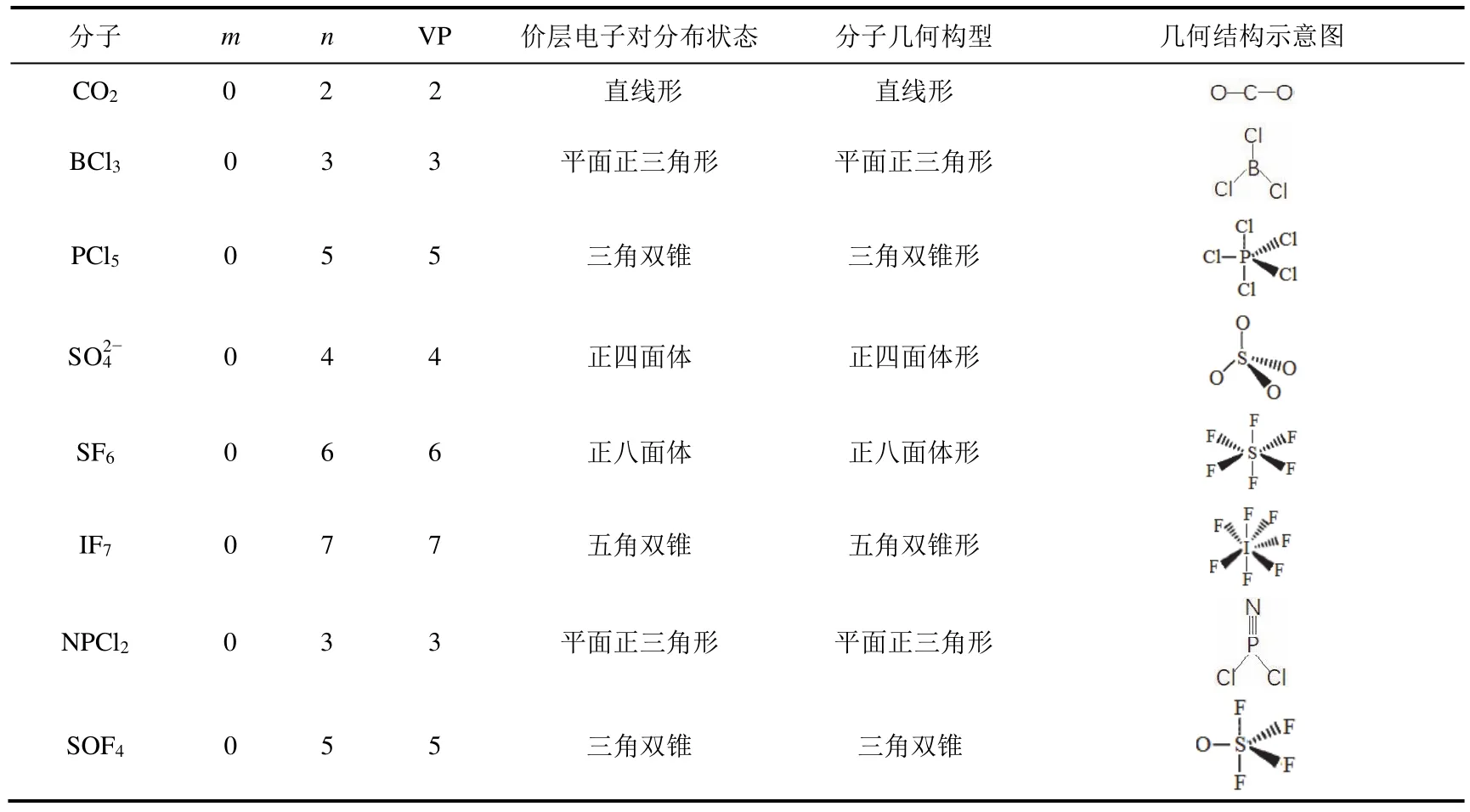
表2 孤电子对数等于零的分子结构推测实例

2) 孤电子对数不等于零的分子或离子，其几何构型与价层电子对构型不一致，需要通过不同类型的电子对之间的排斥力大小来排布配位原子的位置。表3给出了推测这类分子结构的一些实例。

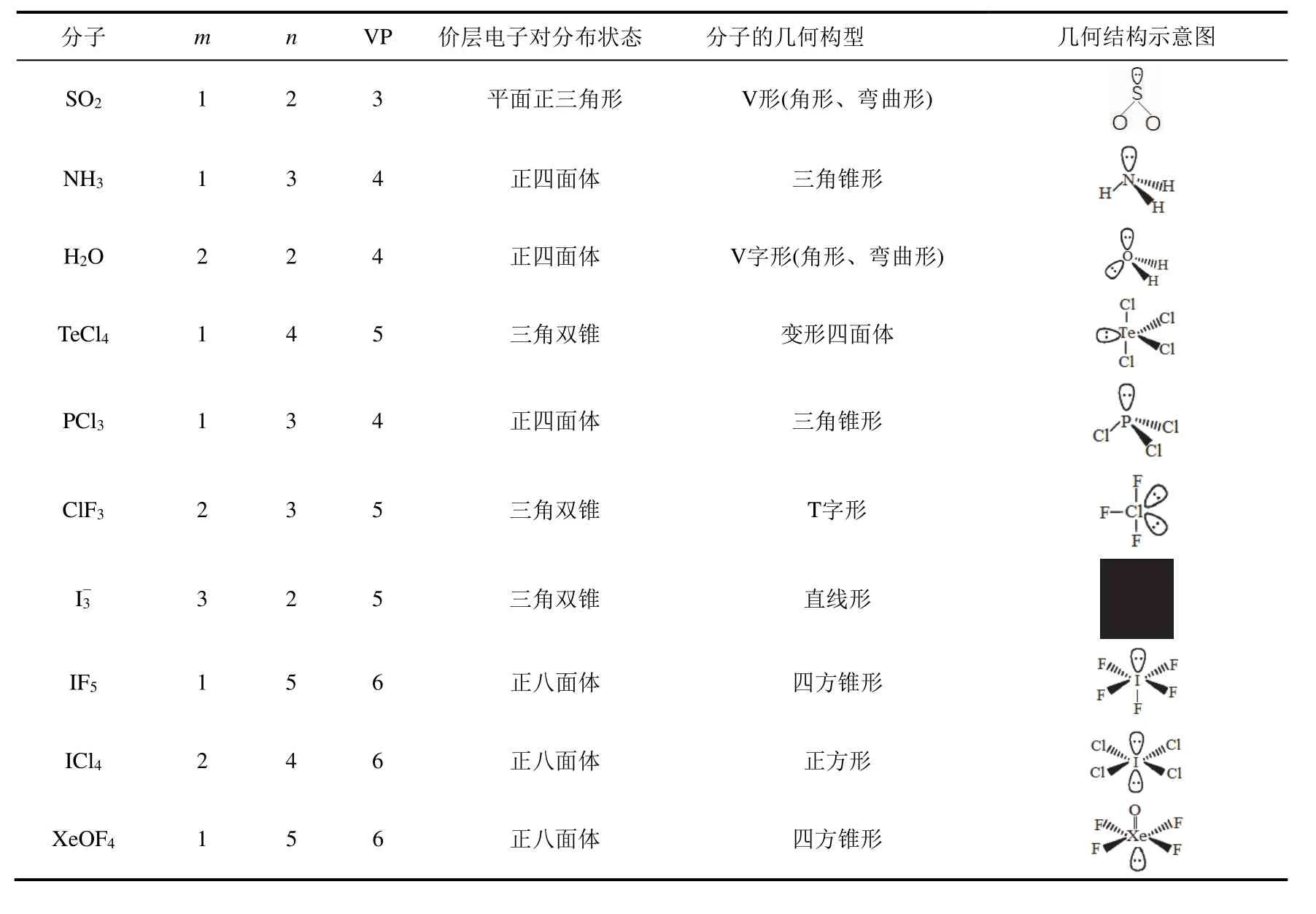
表3 孤电子对数不等于零的分子结构推测实例

3) 孤对电子、π键和配位原子的电负性会对键角产生一定的影响。孤对电子距中心原子近，对相邻的σ键电子对具有较大的排斥力。同样，π键电子也对相邻的σ键电子对也具有较大的排斥力。这种较大的排斥力将会使临近的σ键角变小；中心原子及配位原子的电负性也会使键角发生一定程度的变化。当配位原子的电负性较大时，由其形成的σ键电子对距离中心原子较远，σ键电子对之间的排斥力减小，导致键角减小；反过来，当中心原子的电负性较大时，由其形成的σ键电子对距离中心原子较近，σ键电子对之间的排斥力较大，导致键角增大。

价层电子对互斥理论能够定性的地推测简单分子的几何结构，方法简单、方便，易于理解和掌握。

4 结语

通过对不同教材中关于价层电子对互斥理论的应用方法的分析及对比，虽都能定性地推测出简单分子的几何结构，但有的方法易于理解和掌握，而有的方法不易理解。推荐用中心原子的基态价电子数及配位原子的未成对电子数来确定中心原子价层中的非键电子对数(孤电子对数)，该方法既具有明确的物理意义，又能够准确解释简单分子或离子的几何结构，且简单、易懂、易记，有利于初学者的理解和掌握。