基于影响矩阵法的系杆拱桥吊杆张力计算及拱座空间受力分析

郑 浩， 陈 峥， 左 啸

(湖南省交通水利建设集团有限公司， 湖南 长沙 420008)

下承式拱桥是市政桥梁中常见的结构形式，作为复杂的超静定结构体系桥，主梁承担的荷载通过吊杆传递给拱肋，拱肋、吊杆与纵梁形成整体，共同参与受力。为了达到预期合理的成桥状态，对吊杆张拉顺序以及张力数值需要进行严格控制。王祥国等[1]将影响矩阵法运用于系杆拱桥中，通过建立施工阶段拱桥模型，以吊杆索力优化前后差值向量二范数平方最小值为目标函数建立优化模型，达到减小吊杆张拉次数的目的；李洪波等[2]提出了基于影响矩阵法的综合刚性吊杆法和自动调索法，确定合理成桥吊杆内力；朱利明等[3]基于传统合理成桥吊杆张力计算方法，分析其各自优缺点，并在此基础上通过数据标准化方法对计算结果进行优化，使全桥结构受力更为合理；余睿等[4]基于VBA计算平台，计算在等步长及非等步长情况下吊杆更换过程中张力的变化情况，确定吊杆更换中索力最优转换设计方案；胡忠雯等[5]选取参数与实际工程相同的短吊杆进行了短吊杆室内频率法测试硏究，提出了基于梁振动理论的吊杆索力计算修正模型。

上述学者更多针对其算法进行研究，缺少一定的实际工程数据验证，在实际工程中吊杆张拉顺序以及吊杆索力测试都会影响吊杆索力实际数值。本文结合前人研究成果，基于影响矩阵法，运用Midas建立下承式拱桥有限元模型，计算得出经二次调索后合理的成桥吊杆张力分布，并控制实际张拉顺序及数值，通过修正后的频率-索力系数K得出实测索力数值，与理论计算值进行对比。同时将拱座结构实体化建模，分析此吊杆张力成桥状态下拱座的空间受力情况，提出合理化建议。

1 基于影响矩阵法的二次调索

在下承式拱桥施工过程中，桥面系及拱肋施工完毕，吊杆初张后，需撤除施工用支架，全桥经历体系转换，桥面荷载经由吊杆传至拱肋，此时，受初张顺序以及大小等因素影响，吊杆力未达到预期目标状态，需要进行二次调索。

影响矩阵法用于计算施工阶段以及成桥阶段的吊杆张力调整，实现框架结构调值以及结构优化的统一。该方法当前多应用于斜拉桥合理成桥状态的吊杆张力优化和施工阶段吊杆张力计算，已有资料在系杆拱桥中对吊杆张力优化以及目标张力调整这一方面的运用并不多见。二次张拉阶段，由于所有吊杆均已张拉一定数值，存在初始力，所以张拉任何一根吊杆对其它吊杆的张力均有影响，此时是在所有吊杆均已安装情况下求得相应的影响矩阵。受调和施调向量是同索力影响矩阵一起出现的2个向量，而使用索力影响矩阵可以建立受调向量与施调向量之间的关系。

结构物中心截面上存在的n个独立元素所组成的列向量，它们在整个数值调整过程中通过接受调整来达到某种期望的状态，如式(1)。

D={d1，d2，…，dn}T

(1)

结构物中可以通过指定可实施调整来改变受调向量中由m个独立元素所组成的列向量(前提条件：m≤n。若m>n则会导致未知数个数多余方程数，解则不可确定)，而杆件内力或支座变位组成了其元素，如式(2)。

T={T1，T2，…，Tm}T

(2)

影响向量可以影响矩阵的每一列阵。它的意义是由于某个施调量T(1≤i≤n)的改变而引起受调向量{D}的变化量，记作：Δi={Δ1i，Δ2i，…，Δni}T，当m个施调量均出现单位变化时，就把相应的m个影响向量通过矩阵表示，如式(3)。

(3)

位移、应力和内力这些力学概念都可能是影响矩阵的元素，同时影响矩阵也是他们混合形成的矩阵。一般情况下，可默认施调向量与受调向量之间呈线形关系，即式(4)成立。

{d1，d2，…，dn}T

(4)

2 工程概况

本文在考虑上述影响矩阵法基础上，基于某下承式拱桥实际工程，对吊杆索力情况进行分析。此桥拱肋采用钢箱结构，设2片拱肋。主桥计算跨径80 m，拱肋面内中心线线形为矢跨80 m、矢高16.4 m的二次抛物线，拱肋铅垂面投影矢高为15.4 m，矢跨比1∶5。拱肋为提篮拱形式，拱肋向内倾15.09°。拱肋采用矩形钢箱截面，拱肋截面内高2.0 m，内宽1.6 m。拱肋共划分为9个节段，5种制造类型，节段编号依次为G1～G5。拱肋分段最大长度11.6 m，节段最大重量约21 t。主桥每侧拱肋各设置14根吊杆，吊杆纵向间距为5.0 m，抗拉强度标准值为1770MPa。其桥型布置如图1所示：

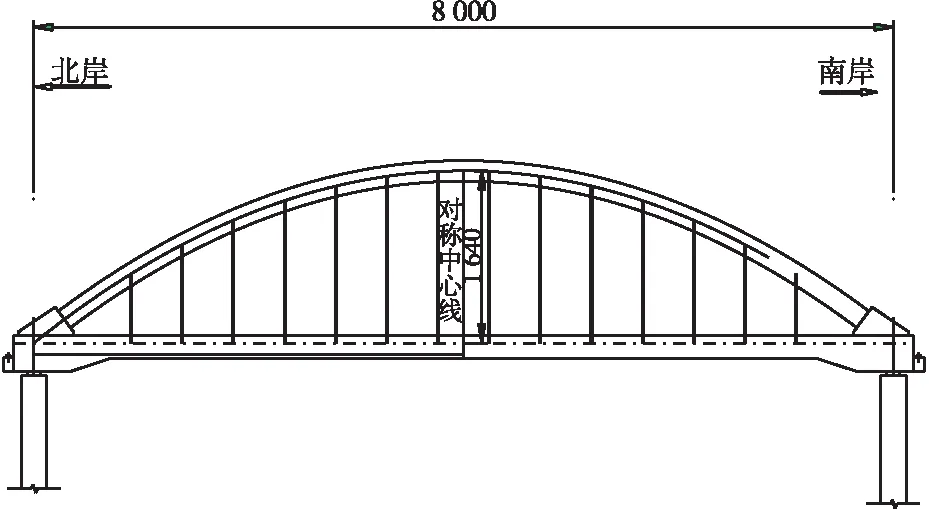
图1 桥型布置图(单位： cm)

3 初张后的二次调索控制

为了确定张拉初值，结合相关资料，拟定二期施工结束后的吊杆索力值作为吊杆的初始张力[6]，其初始张力数值如表1所示。

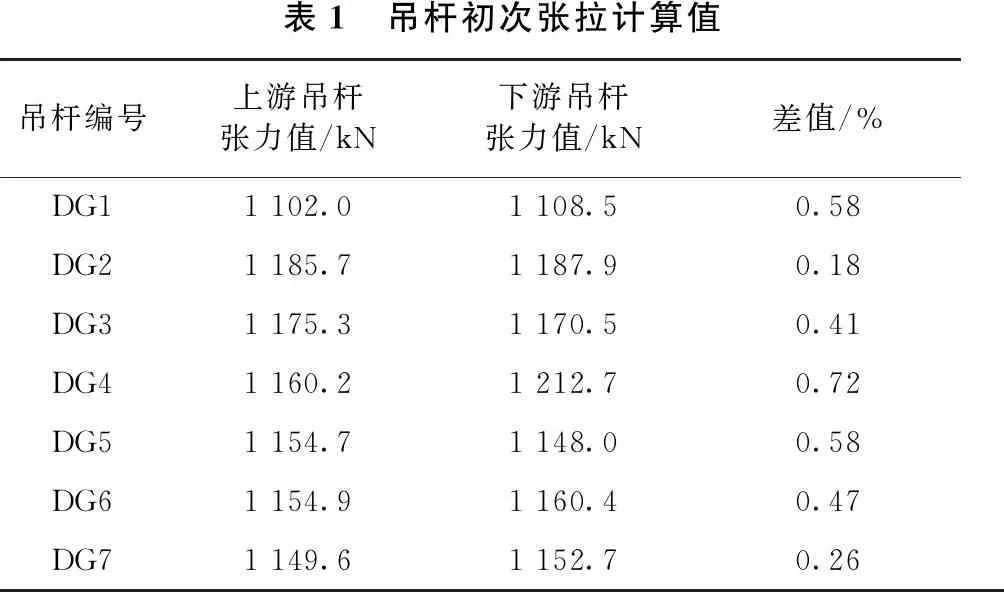
表1 吊杆初次张拉计算值吊杆编号上游吊杆张力值/kN下游吊杆张力值/kN差值/%DG11 102.01 108.50.58DG21 185.71 187.90.18DG31 175.31 170.50.41DG41 160.21 212.70.72DG51 154.71 148.00.58DG61 154.91 160.40.47DG71 149.61 152.70.26

根据表1可知，在不考虑吊杆张拉作用下，端部吊杆因距离支承位置最近，所承受桥面荷载最小，吊杆力最小；在全桥1/4及3/4处附近的吊杆力最大，上下游对称位置处的索力差值均在0.72%以内，南、北向对应吊杆张力差值最大为0.5%，且通过整体结构可知，此桥为标准对称桥梁，因此纵、横向对应位置处的吊杆张拉力取统一数值，拟定张拉力如表2所示。

依据上述结果，运用Midas有限元软件，分别对于每根吊杆施加单位力，得出索力影响矩阵M[7]，得出目标索力，如式(5)所示。

Tm=Tc+M·Td

(5)

表2 吊杆初张控制索力值吊杆编号张拉力值/kN吊杆编号张拉力值/kNDG11 100DG51 150DG21 180DG61 150DG31 170DG71 150DG41 160

式中：Tm为目标索力值向量，Tc为当前索力值向量，Td为施调索力值。

对于索力调整来说，理想状态下，无论张拉顺序如何变化，最终都会得到一个较理想的目标索力；再通过此方法找出单位力作用下桥面位移影响矩阵C，得出位移约束影响下的关系式。

C·TΔ=-X

式中:C为位移影响矩阵，TΔ施调索力向量，X为桥面位移向量。

实际计算中以目标成桥索力以及桥面线形作为控制标准。通过上述2个影响矩阵计算式，参考实际工程及相关资料[8]，拟定吊杆由跨中向拱脚处对称张拉，得出二次调索后的理论吊杆索力。成桥理论吊杆张力对比见表3。

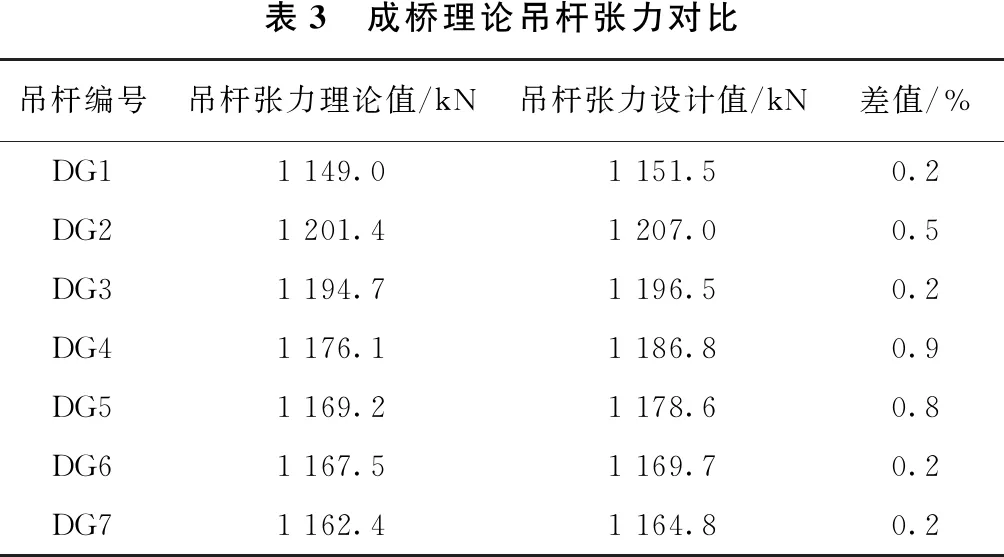
表3 成桥理论吊杆张力对比吊杆编号吊杆张力理论值/kN吊杆张力设计值/kN差值/%DG11 149.01 151.50.2DG21 201.41 207.00.5DG31 194.71 196.50.2DG41 176.11 186.80.9DG51 169.21 178.60.8DG61 167.51 169.70.2DG71 162.41 164.80.2

根据表3吊杆张力理论值指导现场实际张拉工作，待全桥张拉完毕后，使用索力动测仪进行测量，并考虑实际系数K修正，以上游吊杆索力测试对比结果如图2所示。

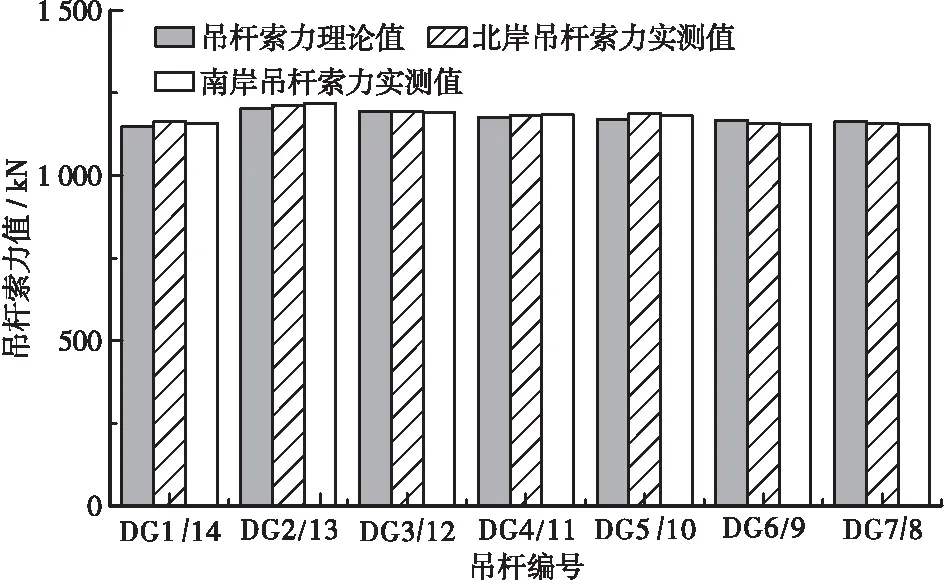
图2 成桥吊杆索力值对比图

由图2数据可以看出，根据上文所计算的成桥吊杆理论索力进行张拉控制，实测数值与理论数值相差较小，最大差值控制在2%之内，且南、北两岸对应位置处的数值基本一致，全桥吊杆索力分布较为均匀，达到了预期效果。

4 合理成桥索力下的拱脚空间受力分析

4.1 有限元模型建立

根据图纸设计参数及相关理论，运用Midas Civil有限元软件建立有限元模型，全桥共离散成8917个节点。拱肋以及桥面构造采用梁单元模拟，吊杆选用只考虑轴向受力的桁架单元模拟。选取某一拱脚结构进行实体化建模，拱脚混凝土材料假定为线弹性体，共划分为7290个实体单元，拱肋与系梁在对应位置处与拱脚单元节点采用主从刚性连接，二期荷载通过3道虚拟梁来施加，每道虚拟梁24.8kN/m，其模型如图3、图4所示，模型材料参数如表4所示。

图3 桥梁有限元模型示意图

图4 拱脚位置连接示意图

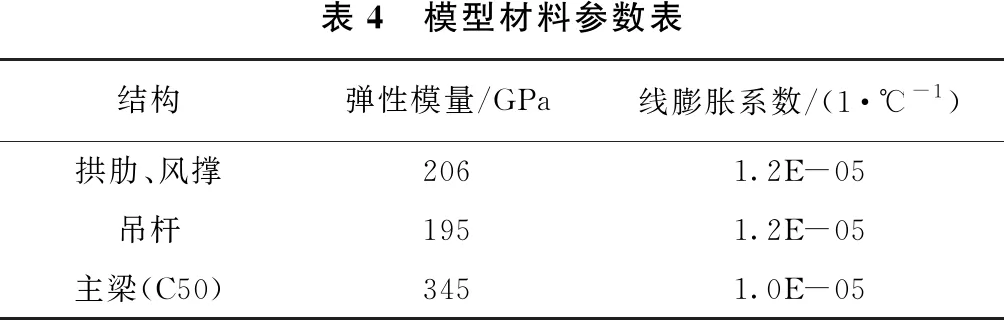
表4 模型材料参数表结构弹性模量/GPa线膨胀系数/(1·℃-1)拱肋、风撑2061.2E-05吊杆1951.2E-05主梁(C50)3451.0E-05

4.2 拱脚处受力分析

依据上述吊杆实测数值，通过初拉力荷载形式将其作用在模型中，为了方便计算分析，此处仅建立一次成桥施工阶段，不考虑收缩徐变影响，其受力如图5所示：

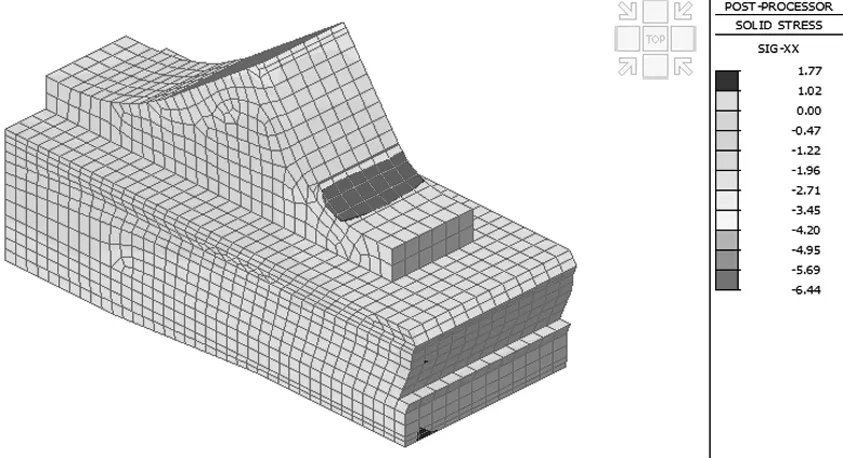
a) 拱座X向应力结果

b)拱座Z向应力结果

根据上述结果可以看出，X、Z向拉、压应力最大值主要出现在拱肋与拱脚结合位置，由于受到拱肋轴向力作用，拱座正面(与拱肋结合面)会向着背面方向发生压缩变形，拱座圆弧位置处混凝土受拉，拱座背面受压，其Z向拱座正面最大拉应力为1.87 MPa，拱座背面最大压应力为-11.54 MPa，其正面圆弧处拉应力已超过混凝土轴心抗拉设计值1.83 MPa，需要对于此处进行配筋加强，同时也可考虑优化局部形状，改善其结构应力分布。

为了验证上述观点，提取拱座位置X向变形结果见图6。根据图6所示，拱座顶部正面位置总体变形指向X轴负向，而在圆弧处变形方向与顶部相反，由此可知圆弧位置为拱座变形交界处，混凝土受到不同方向作用力的张拉，后期桥梁运营期间对于此处需着重监测有无裂缝出现。

图6 拱座位置X向变形结果(单位： mm)

5 结论

运用影响矩阵法结合全桥有限元模型，得出了二次调索后成桥吊杆理论索力值，同时基于上述计算所得吊杆张拉力，通过频率-索力修正系数K求得实际吊杆索力值，并与理论值进行对比，分析了成桥状态下拱座的空间受力情况，结果表明：

1) 拱桥成桥合理索力不仅与张拉力大小有关，且张拉顺序的拟定以及二次调索的控制都会影响成桥索力情况。

2) 利用Midas有限元模型，寻求各向量矩阵之间关系，得出全桥合理成桥理论索力，与设计值相比最大误差仅0.9%；与实测数值进行对比，最大差值小于2%，且吊杆整体索力均匀。

3) 根据模型计算结果，Z向拱座正面最大拉应力为1.87 MPa，拱座背面最大压应力为-11.54 MPa，需对此处进行配筋加强，或对拱座几何构造进行优化，使得受力更为合理。