相控地质统计学反演方法及其在油田开发中的应用

段新意，李尧，郭军，谭辉煌

（中海石油（中国）有限公司天津分公司渤海石油研究院，天津 300452）

0 引言

地震属性、90度相移和约束稀疏脉冲反演等作为传统地震储层预测方法中行之有效的重要技术手段，在勘探阶段发挥了重要作用，但是由于其成果的分辨率不够高，难以满足油田开发阶段的精度需求［1］。新近系地层是渤海油田主要目的层系之一，沉积特征主要为极浅水三角洲相沉积和河流相沉积，复杂的沉积环境导致该层系储层厚度较薄，在纵向和横向上相互叠置交切，且储层内部多发育泥岩隔夹层。由于原始地震资料频带范围有限，基于传统反演技术得到的储层预测结果无法有效地表征储层及内部泥岩隔夹层的发育情况。同时，经过数十年的开发生产，油田产量递减现象明显，需要对新近系油田实施综合调整以保证油田稳产。作为开发井和注水井网设计的资料前提和参考依据，储层发育情况的准确刻画至关重要［2-4］。

常用于储层预测的地震反演方法主要分为确定性反演和随机反演两大类。约束稀疏脉冲反演方法属于确定性反演方法，反演结果为最佳波阻抗体；地质统计学反演方法属于随机反演的范畴，为一系列等概率实现的平均结果［5-6］。地质统计学反演是将传统的地质统计学技术和地震反演技术相结合，利用地质、地震和测井等多种先验信息获得高精度反演结果的一种反演方法，反演结果对于设计油田的注水井网和规避水平井实施风险具有重要的指导意义［7-11］。

地质统计学反演方法由 Bortoli等［12-13］提出，Rothman［14］和 Dubrule 等［15］进一步发展并应用于三维实际数据中。早期地质统计学反演方法的主流算法为序贯高斯等方法，虽然能有效地改善基于克里金插值方法导致的模糊平滑效应，但也降低了反演结果的横向分辨能力。目前应用最为广泛的是Torres-Verdin等［16］提出的马尔科夫链蒙特卡洛算法（MCMC），该算法首先保证反演结果在参与井位置处与测井结果高度一致，而在远离井位置处主要参考地震数据，这样使得最终的反演结果既在纵向上具有高分辨率，又保证整体反演结果与地质规律更加吻合，在此基础上各类优化算法的出现使得地质统计学反演方法在实际应用中更加成熟和完善［17-33］。

但是常规地质统计学反演方法对于参与反演的先验输入信息要求较为严格，在测井信息不足和不规则井网条件下，相较于常规反演，地质统计学反演并没有明显的优势。于兴河等［25］提出了针对河流相储层的相控随机建模约束方法，它是以沉积相的空间展布特征为依据对随机建模过程进行约束，进而得到精度较高的储层建模结果。闵小刚等［32］提出在准确认识沉积微相空间分布的基础上，将沉积微相建模与储集物性双重变差函数分析相结合，以实现对薄储层物性的高精度反演。上述2种相控方法主要体现在建模和反演参数调节的过程中，并且对沉积相研究要求较高，在沉积环境复杂、沉积相认识不清的地区应用较为困难。

本文模拟分析了变差函数对反演结果的影响，以多属性统计分析结果为基础，建立沉积相等分类结果与地层砂地比分布情况之间的对应关系；然后，将地震地质认识等已知信息转化为不同维度的砂地比约束条件，替代常数砂地比约束（不变）；最后，建立了一种基于相控约束的地质统计学反演方法，并将该方法在渤海A油田和E油田进行了应用，应用效果良好。

1 方法原理

地质统计学反演是以测井和地震资料为基础，在地质框架模型的约束下，分析储层参数进行统计学建模，然后通过贝叶斯判别和MCMC算法获得多个等概率的反演实现，最终的结果为多个反演实现的平均岩性概率体。如果想要获得准确的地质统计学反演结果，需要大量的已钻井参与反演准备过程中的数据重采样等工作。为了获得更加合理而精细的储层预测结果，本文通过一系列模拟分析，提出了适用于先验信息不完备地区的相控地质统计学反演方法。

1.1 变差函数

变差函数γ（）h 主要反映的是岩性（离散属性）和弹性参数（连续属性）的结构性和空间变异性。其中，横向变差函数大小主要影响储层的横向展布规律，纵向变差函数大小主要影响储层的厚度（见图1）。由于不同研究区的地质情况及储层的发育尺度差异较大，因此，需要基于地质认识、测井和地震数据选取合理的纵向和横向变差函数。

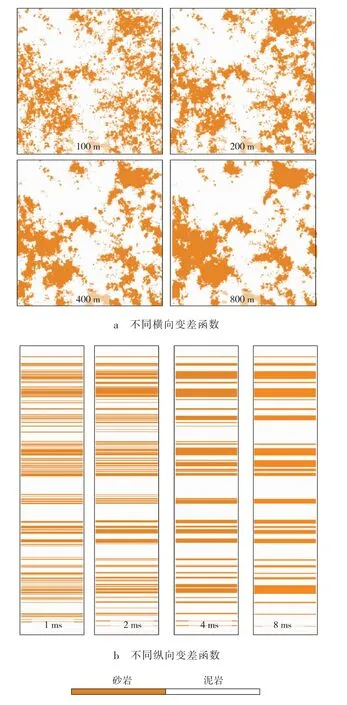
图1 不同纵横向变差函数大小模拟结果

影响反演结果的因素除了变差函数的大小，还有选取的变差函数类型。在进行地质统计学反演时常采用的变差函数类型有3种：指数型、高斯型和球型。其中，指数型模拟结果最为离散，表示储层横向展布范围有限，常用来描述沉积环境不稳定的情况（如陆相沉积）；高斯型模拟结果最为连续，表示储层横向展布范围较大，常用来描述沉积环境稳定的情况（如海相沉积）；球型模拟结果介于两者之间。

由于不同地区具有复杂多样的地质沉积特征，直接采用上述3种类型的变差函数难以有效反映储层发育情况。为了适应复杂地质条件，较为准确地表征其储层发育情况，可以采用指数型与高斯型变差函数组合的方式，也就是更加灵活的混合型变差函数。

混合型变差函数：

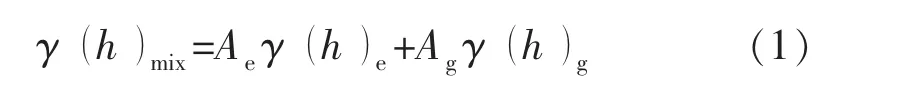
式中：h为滞后距（主要控制储层展布范围），m；γ （h ）e，γ （h ）g分别为指数型和高斯型变差函数；Ae，Ag分别为指数型和高斯型变差函数的权重因子（Ae+Ag=1）。

由二维模拟结果（见图2）可以看出：混合型变差函数模拟结果的横向稳定性介于指数型和高斯型变差函数模拟结果之间。混合型变差函数的表达形式更加灵活多样，通过调节指数型和高斯型变差函数的权重系数，可更加准确地模拟复杂地质条件下储层发育情况，这对在复杂储层发育区开展地质统计学反演具有重要意义。

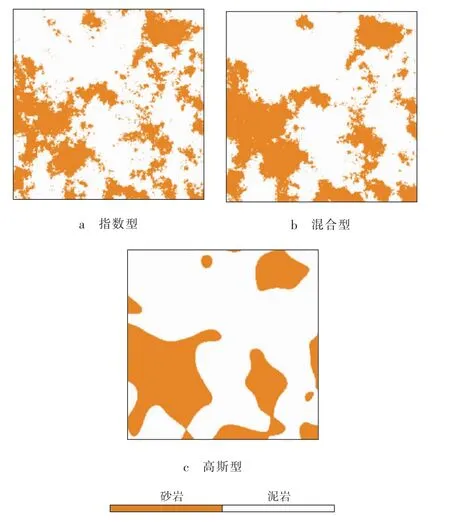
图2 不同类型变差函数二维模拟结果

1.2 相控条件

一般在进行地质统计学反演时，各个目的层段离散属性的砂地比信息为固定的常数值，它来自于目的层段测井数据统计分析的平均值。砂地比为常数表示该目的层段各空间的砂地比分布是固定的，但实际情况下砂岩和泥岩在地层中的分布是随机的，因此，在缺少参与井的地区，如果将砂地比设置为常数，会导致与实际地层砂地比真实分布差异较大。为此，本文以渤海油田新近系的地质沉积环境基础，同时结合开发油田钻井信息，提出了相控地质统计学反演方法。该方法以地震地质特征对应情况的综合分析出发，建立地震测井等先验信息与地层砂地比的对应关系，将得到的不同维度的砂地比信息代替常数砂地比，对反演过程进行约束，从而获得了更加准确的高分辨率反演结果。

1.2.1 一维相控

在储层横向发育稳定且在纵向上分布规律性明显（如富砂型的辫状河三角洲沉积）的情况下，进行地质统计学反演时，基于测井信息统计得到的一维相控约束能够更加准确地反映储层在纵向上的发育规律。以富砂型沉积环境下的新近系X油田为例，该油田目的层段顶部发育1套分布稳定的厚储层，基于已有地质认识和地震反射特征，并结合目的层段沉积旋回特征，通过多井交会分析，建立了测井岩性与砂地比的对应关系，从而得到能够反映各目的层段纵向砂地比变化情况的一维相控条件（见图3）。

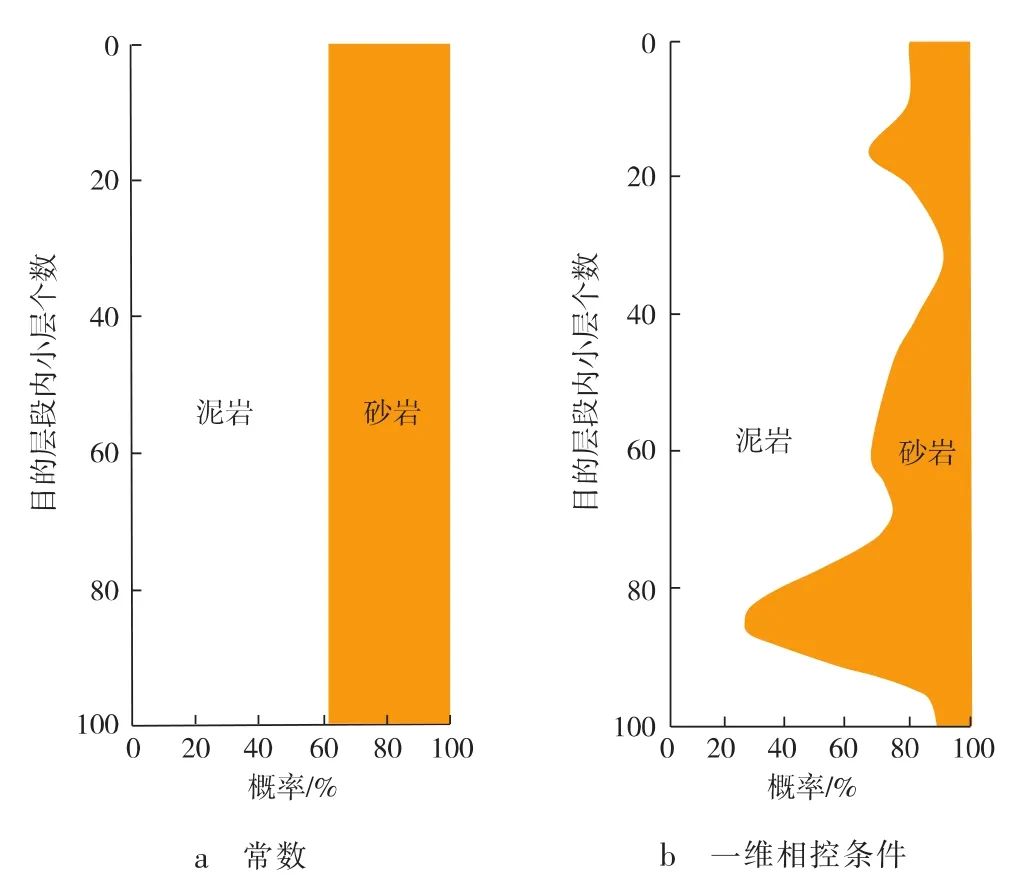
图3 目的层段砂地比分布示意

由地质统计学反演的模拟结果可以看出 （见图4）：砂地比为常数情况下的模拟结果在约束井附近与测井揭示的砂泥岩对应较好，在远离约束井位置处，砂泥岩杂乱分布，不具地质规律；一维相控条件约束下的模拟结果有了明显的改善，不但与约束井的砂泥岩对应关系更好，而且在远离约束井位置处也能够准确指示目的层段顶部大套储层发育的特征，与本地区的地质情况一致。

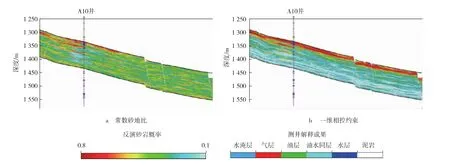
图4 模拟结果对比

1.2.2 二维相控

当目标区内储层或泥岩隔夹层在横向上发育不稳定，且纵向上不具有明显的规律性时（如曲流河沉积），砂地比为常数、一维相控条件都难以准确反映储层的分布特征。为了得到更为准确的反演结果，首先，在沉积相的基础上进行地震相研究，根据已钻井结果，建立地震相与平面砂地比分布的对应关系；然后，将地震相分析结果转化为横向砂地比分布结果，即为二维相控条件。

对某典型的三角洲相沉积油田进行分析得出，该油田目的层段储层横向变化快（见图5）。如果直接运用测井结果进行横向插值，最终得到的平面砂地比分布会出现明显的“牛眼”现象，这与目的层段实际地质情况不符。利用二维相控条件就可更加合理地描述目的层段的砂地比平面展布。

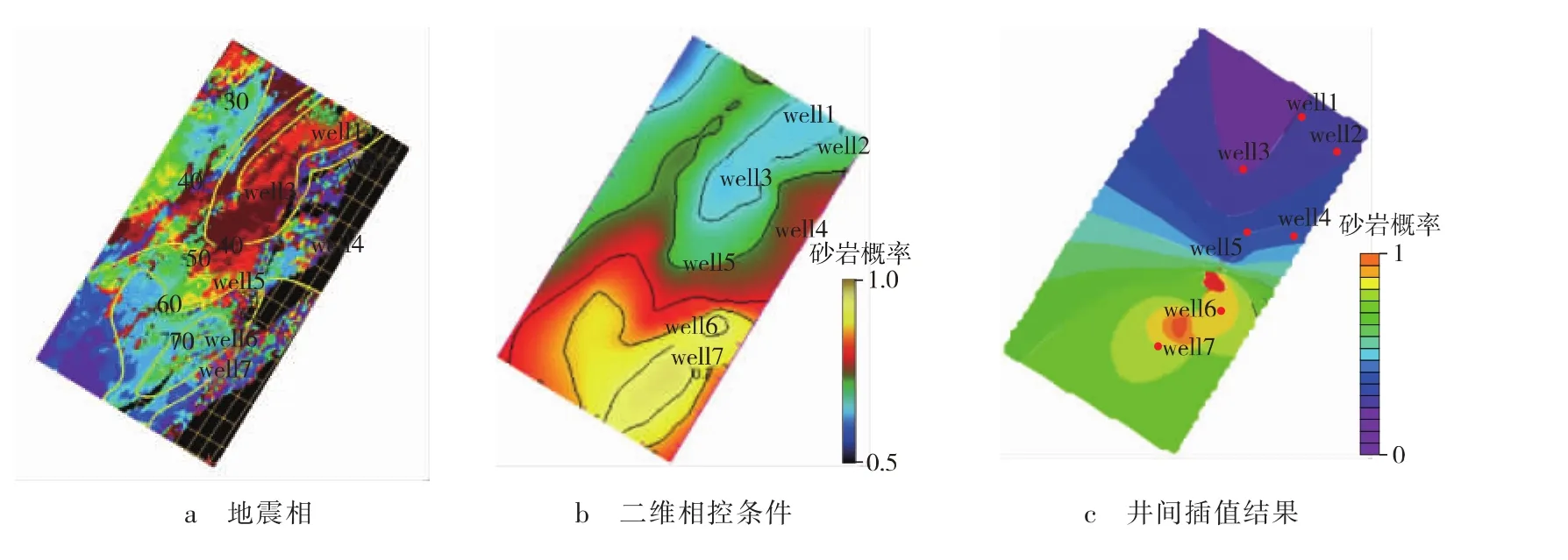
图5 地震相及砂地比平面分布

1.2.3 三维相控

如果储层发育具有明显的规律性，那么根据先验信息可以得到一维或者二维的砂地比信息作为相控约束条件，进而得到更为合理的储层预测结果。但是在储层发育规律性差的地区 （如极浅水三角洲相沉积环境），一维和二维约束难以适用。当井上资料的弹性参数能够有效区分储层与非储层的目标区时，首先开展常规的叠后波阻抗反演，将得到的反演结果与已钻井岩性解释结论相结合，通过建立目的层段的叠后反演结果与地层砂地比之间的对应关系，就可将常规叠后波阻抗反演结果转化为约束地质统计学反演的三维砂地比分布概率体（见图6）。

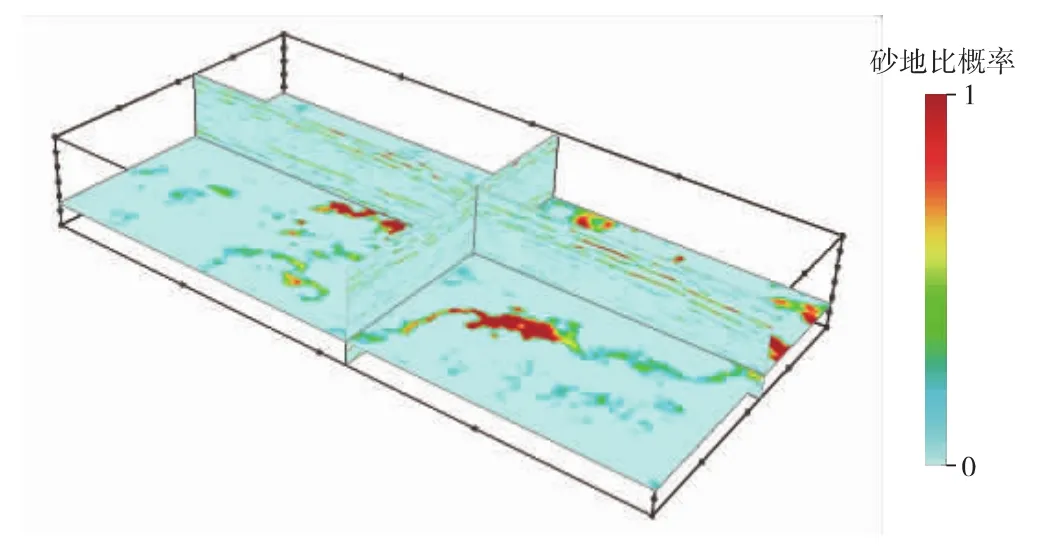
图6 三维相控条件

在气云和火成岩等特殊地质体发育区，特殊地质体的地震反射特征与研究目标反射特征相互混淆，影响了反演结果的准确性。渤海某油田火成岩发育，火成岩在地震剖面中表现为强反射，屏蔽了火山岩下部储层的能量，最终的反演结果中，火山岩体表现为良好的储层响应，但这与实际情况不符。为了减弱特殊地质体对反演结果的影响，采用了三维相控的思路，削弱特殊地质体对地质统计学反演结果的影响。首先，通过自动追踪或人工拾取的方法在常规叠后反演结果中刻画出特殊地质体的空间发育范围；然后，将其与预先得到的三维砂地比信息进行融合，适度平滑后得到用于约束反演的三维相控条件。该思路能够使得地质统计学反演方法更加灵活地应用于特殊地质体发育区。

2 应用效果

2.1 渤海A油田

A油田是渤海海域典型的新近系油田，位于渤海海域的东部，目的层段馆陶组为辫状河沉积，主要发育砂岩和泥岩，薄储层在空间上广泛发育。油田目的层段地震资料主频为20 Hz左右，频带范围为7～ 65 Hz，常规反演方法的储层预测结果分辨率低，无法准确反映薄储层的空间分布和厚度。由于储层展布情况不明确，导致油田开发过程中出现注采关系矛盾的现象。为了进一步保证油田大规模综合调整的顺利实施，明确注采关系，因而对该油田目标层段开展了相控地质统计学反演工作。

该油田开发井缺少声波测井资料，对油田范围内所有的探井和开发井测井曲线统计发现，该油田储层测井整体表现为低密度特征，密度曲线能够有效地区分砂岩和泥岩（见图7），因此，将密度转化为拟波阻抗，作为反演的连续属性。

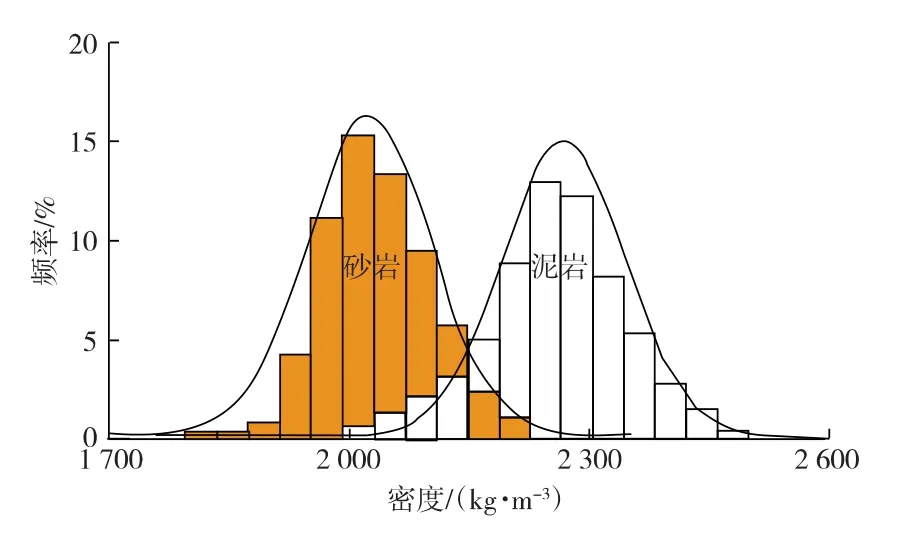
图7 砂泥岩密度分布直方图

由于海上井网分布的局限性，在缺少井控的地区，常规地质统计学反演方法难以获得准确的储层预测结果，而采用相控地质统计学反演能够有效地提升反演结果的准确性。虽然对于A油田的薄层平面展布认识不清，但是根据该油田富砂型辫状河沉积的特征，以及目的层段主力砂体纵向上具有明显的规律性，且横向上分布较为稳定，因而采用基于一维相控约束的地质统计学反演。通过对目标区已钻井测井曲线及解释结论的分析，建立了测井岩性与砂地比分布的对应关系，获得目的层段L1，L2，L3，L4四个油组的一维相控条件（见图 8）。

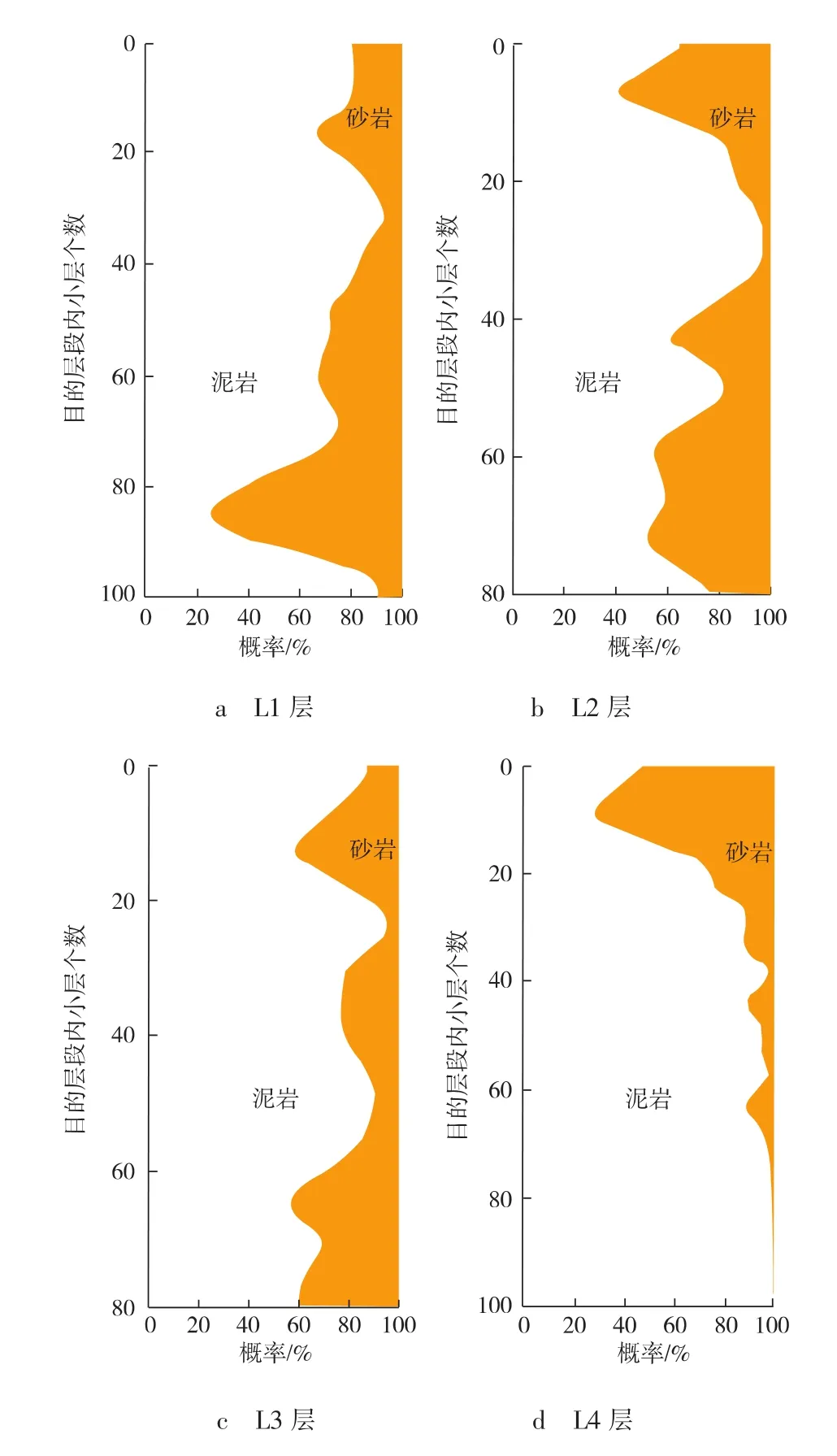
图8 各层段一维相控条件示意

同时，在反演参数设置过程中，充分考虑了该油田的地震地质情况和钻井情况，优选变差函数类型及大小。在进行参数优化的基础上，得到了相控地质统计学反演结果（见图9）。

由图9可以看出，地质统计学反演结果中储层发育形态与原始地震资料中同相轴走向对应关系较好，相对于常规90度相移结果，地质统计学反演结果的分辨率明显提升，参与井（A6，A7井）和验证井（A5井）处地质统计学反演结果的储层厚度与已钻井揭示的储层厚度具有很好的对应关系，相控之后的反演结果与已钻井揭示的储层厚度吻合度更高。

图9中，常规地质统计学反演结果的薄储层展布明显受到参与井强制约束，地质规律性差，井间薄储层发育情况出现明显的“离井即断”现象。同时还可看出，相控地质统计学反演结果不但能够在纵向上准确刻画薄储层厚度，而且能够更好地描述薄储层在横向上的展布特征，储层分布范围更加符合地质规律。

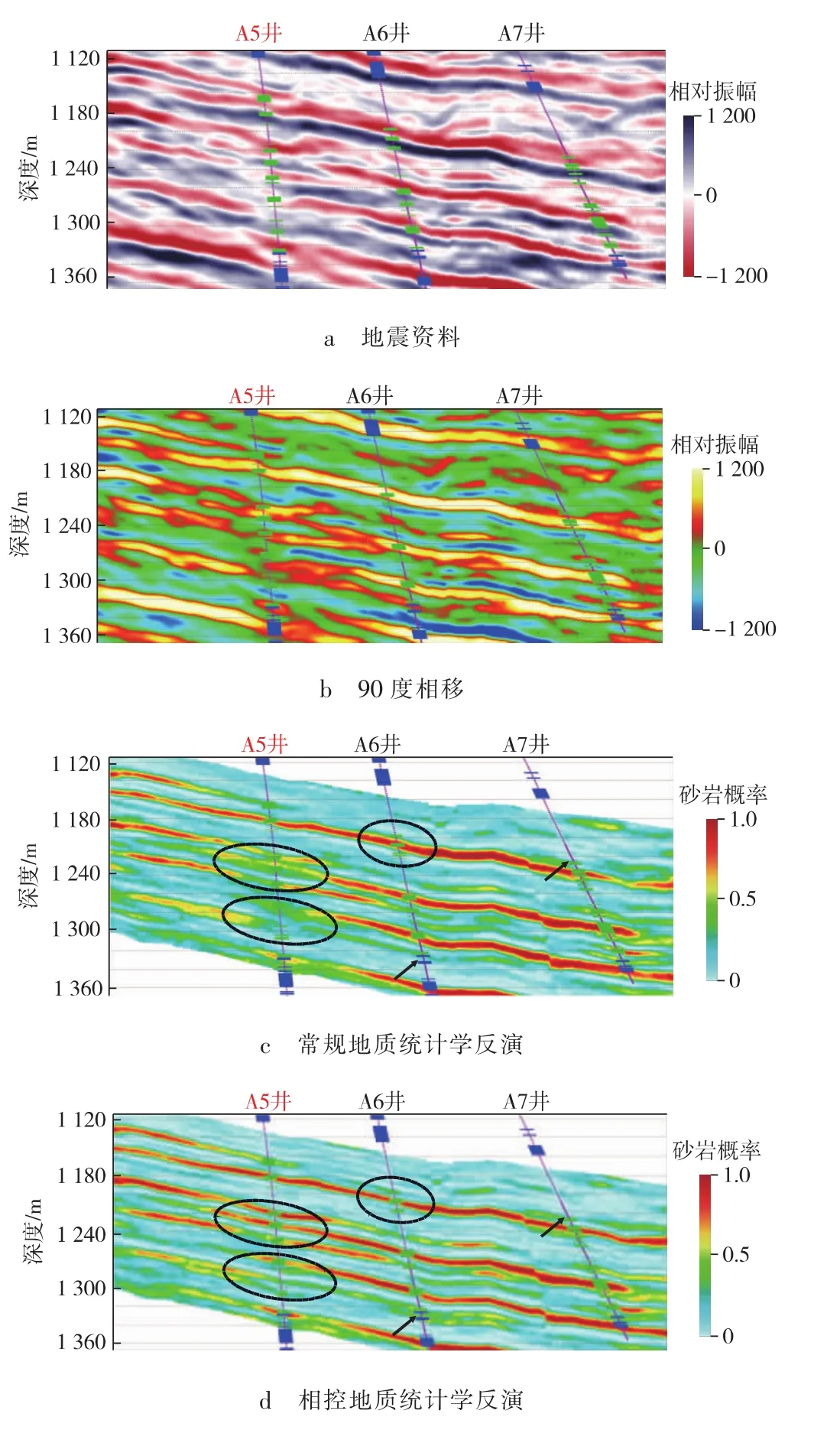
图9 反演结果对比

在油田开发中发现，开发井A2井在目的层段内的储层存在不同程度的水淹现象，该井主要受注水井A1和A3的影响（A1井参与反演，A2和A3井未参与反演）。由于常规基于90度相移的储层预测结果分辨率低（见图10a），无法有效描述储层的展布特征和连通性，所以难以准确判断A2井不同小层的水淹现象具体是受A1井还是A3井的影响。相控地质统计学反演结果分辨率明显高于常规储层预测结果 （见图10b），从连井剖面中能够清晰地追踪各小层的横向展布情况和储层的连通性 （如图10b中黑色虚线所示），能够准确地解释A2井不同小层的水淹来源。将图10b中小层的平面属性对比得出 （见图11），A2井小层的水淹现象是受注水井A1的影响。

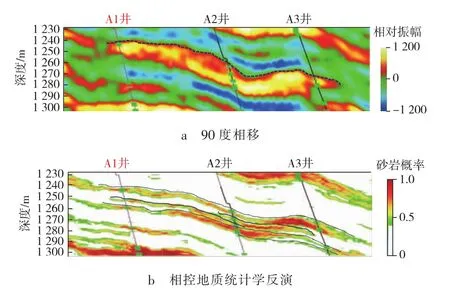
图10 储层预测结果对比

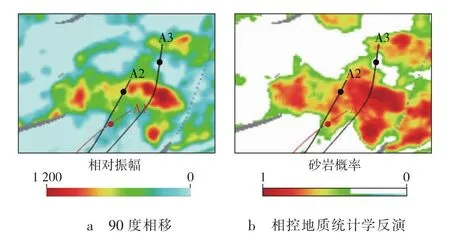
图11 储层预测平面属性对比

2.2 渤海E油田

E油田位于渤海海域的中部，主要目的层新近系明化镇组为典型的曲流河沉积，砂体厚度较大，部分砂体内部发育厚度较薄的泥岩隔夹层。常规稀疏脉冲反演等储层预测方法难以准确描述厚度较大的储层及厚度较小的泥岩隔夹层，无法满足开发注水方案设计的需求。

结合该油田已钻井，对目标区目的层段开展了常规地质统计学反演和相控地质统计学反演研究。由于该油田主力砂体平面分布稳定，因此结合已有地震地质信息，建立了用于相控地质统计学反演的二维相控条件。

E11注水井与E12h开发井相距300 m左右，在油田开发过程中，E11井注水后，E12h井受效不明显，而E13h井受效明显。常规反演结果显示两者之间储层发育稳定 （见图12），常规地质统计学反演结果中显示E12h井与E11井之间有薄泥岩隔夹层发育。而相控地质统计学反演结果中能够更加清晰地看到泥岩隔夹层的发育位置（图12c中黑色虚线所示）。

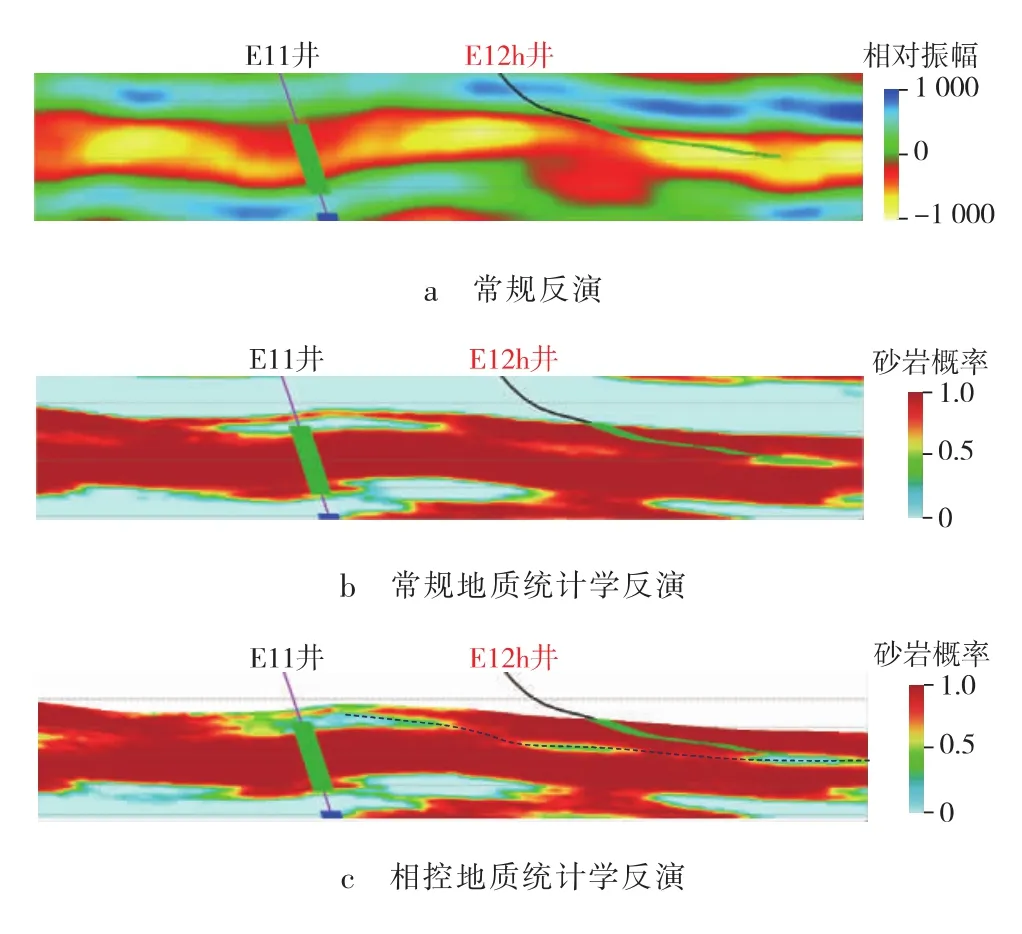
图12 目的层段储层预测结果

在图13所示的平面属性图中，更加清晰地看到E11与E12h井之间泥岩隔夹层的发育形态，该泥岩隔夹层的存在导致E12h井受效不明显。

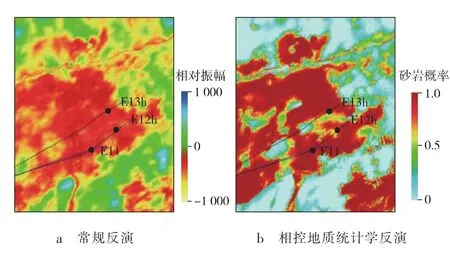
图13 目的层段储层预测平面属性

基于高精度相控地质统计学反演结果，能够明确油田开发过程中的注水受效问题，而且也为后续开发井网设计提供重要的资料基础和参考依据。

3 结束语

地质统计学反演方法得到的高精度反演结果对于薄层有较好的反映，但是在井网分布不均匀和地震资料品质较差的地区，加入更多合理的先验信息作为约束条件，就能够得到更加准确的反演结果。本文详细分析了不同储层发育特征，将测井信息、地质认识与地震反演有机结合，提出了相控地质统计学反演方法。相控地质统计学反演结果不但具有高精度的优势，而且更加符合地质规律，能够为复杂储层发育区的开发井网设计和泥岩隔夹层发育区的水平井实施提供重要的参考依据，对油田开发阶段调整井实施具有重要意义。