矿物组成对页岩油渗流机理的影响

曹小朋

（中国石化胜利油田分公司勘探开发研究院，山东 东营 257015）

0 引言

目前，页岩油主要采用多级压裂水平井技术开发。原油从页岩基质流到层理缝中，再经过压裂缝网流向水平井筒，从而实现页岩油的有效动用。由于页岩基质主要发育纳米级孔隙，岩石表面强相互作用对流体的影响不可忽略，因此页岩油的赋存状态和流动机理与常规油藏显著不同［1-5］。此外，页岩的矿物组成非常复杂［6-8］，其中不但含有丰富的有机质，还含有大量的无机矿物，如石英和方解石等。不同矿物表面性质的巨大差异造成原油的流动规律也可能存在较大不同。因此，深入研究不同矿物孔隙内页岩油的流动机理，对准确构建页岩油渗流模型和后续产能预测具有重要意义。

传统的实验手段和数值模拟方法难以揭示页岩纳米孔内原油的微观流动机理［9-11］。因此，已有相关研究主要采用分子动力学模拟方法开展，且主要针对的是页岩有机质孔隙［12-14］。 Supple 等［12］的分子动力学模拟结果表明，癸烷在碳纳米管内会发生快速的自发渗吸。Zhang等［13］通过真空自吸实验研究了油在有机质孔隙内的流动，并提出了孔隙/干酪根双扩散层模型。Whitby等［14］对非晶态碳纳米管内烷烃的流动进行了实验研究，观察到烷烃的快速流动现象。但单独研究有机质孔隙内原油的流动，并不能清楚认识页岩复杂孔隙网络内的流动规律［15-17］。目前，无机矿物孔隙内页岩油流动规律的研究极为有限，不同化学组成的纳米孔内页岩油流动规律的差异尚不清楚。本文以济阳坳陷页岩油为研究对象，针对页岩的典型矿物组成，以正辛烷为例，研究了不同矿物孔隙内烷烃的流动规律，以期为页岩油渗流数学模型的建立奠定基础。

1 模型与方法

1.1 模型构建

济阳坳陷烃源岩主要分布在沙河街组沙三段底部（Es3x）和沙四段上部（Es4s）。勘探研究已经证实这2个层段中页岩油资源潜力巨大，具有工业化开发价值。济阳坳陷页岩中方解石和石英占比超过60%［18］，同时含有丰富的有机质，因此本文主要针对有机质、方解石和石英组成的纳米孔隙开展研究。

现有文献在研究页岩有机质孔隙内烷烃的吸附特征和流动规律时，一般将有机质的固体壁面简化为石墨烯［19］（见图1a）。本文中有机质孔隙的表面尺寸为2.952 nm×2.556 5 nm，碳原子的势能参数采用OPLS力场描述［4］。由于方解石104晶面的热力学状态最为稳定，因此，从方解石的晶胞中切出104晶面，然后利用2个完全相同的104晶面构建方解石孔隙的固体壁面（见图1b）。它在x和y方向的尺寸分别为3.24 nm和3.0 nm。方解石表面上各种原子的势能参数采用Xiao等［20］所建立的模型进行描述。石英孔隙的壁面由2个100晶面组成，表面尺寸为2.95 nm×2.70 nm（见图1c），同时对石英晶面进行羟基化处理。构成石英表面的原子势能参数采用CLAYFF力场进行描述［21］。

将一定数量的正辛烷分子堆积到给定尺寸的模拟盒中，构成页岩油分子结构模型，然后将其嵌入到上述孔隙结构模型中，由此得到页岩油纳米孔内烷烃流动的模拟模型（见图1）。正辛烷分子的势能参数通过OPLS-AA力场描述［4］，采用几何平均混合准则计算正辛烷与有机质、方解石和石英之间的非键结势能。同时为了提高模拟计算效率，采用particle-particle particlemesh算法计算原子之间的长程静电作用力。

图1 不同矿物组成纳米孔内正辛烷流动的分子模拟模型

1.2 分子动力学模拟方法

为了得到稳定的初始构型，模拟过程中首先采用共轭梯度算法不断调整原子坐标，避免原子重叠。随后在正则系综下进行平衡分子动力学模拟，时间步长为10-15s，并采用Nosé-Hoover热浴调节体系温度。在体系达到平衡后，对孔隙内正辛烷的每个原子施加一个平行于固体壁面的驱动力，以此来模拟定压力梯度下页岩油在不同矿物孔隙内的流动状态。模拟时间为24×10-9s，其中，前 4×10-9s使体系达到动态平衡，后 20×10-9s用于收集原子的运动轨迹并进行统计分析。

由于分子动力学模拟直接得到的是每个原子的位置、速度和受力等，因此为了得到孔隙内流体的密度、速度分布等，需要利用统计力学对模拟结果进行处理。在孔隙内沿着与固体壁面平行的方向上划分多个微元，则每个微元内烷烃分子的密度和速度［22］分别为

式中：ρ为密度，g/cm3；v 为速度，m/s；i为微元内原子序号；N为微元内原子的总数；mi为原子i的质量，g；A为固体壁面的表面积，cm2；Δz为微元宽度（z为垂直于固体壁面方向上微元的位置），cm；vi，x为微元内原子i在x方向的速度分量，m/s。

2 纳米孔隙内正辛烷流动的基本特征

在对不同矿物孔隙内正辛烷流动规律进行对比之前，首先以方解石为例，分析正辛烷在方解石纳米孔隙内的密度和速度剖面。

如图2所示，正辛烷的密度剖面关于孔隙中央对称，且孔隙中央处的烷烃密度基本不变，约为0.672 g/cm3，与该温度和压力条件（353 K，30 MPa）下正辛烷的体相流体密度0.686 g/cm3［23］非常接近，表明孔道中央处的烷烃接近于游离态。而在靠近固体壁面处，正辛烷的密度分布曲线上出现4个峰值，表明形成了4个明显的吸附层。吸附层的厚度可以通过密度分布曲线上相邻2个波谷之间的距离得到。每个吸附层的厚度平均为 0.45 nm，这与 Dijkstra［24］的实验结果（0.4～ 0.5 nm）一致。第1吸附层的峰值密度（约为2.13 g/cm3）远大于第2吸附层的峰值密度（约为0.99 g/cm3），且为孔隙中央流体密度的3.16倍，表明远离壁面造成流体与壁面之间的相互作用力逐渐减弱，页岩油的聚集状态由稠密变为稀疏。

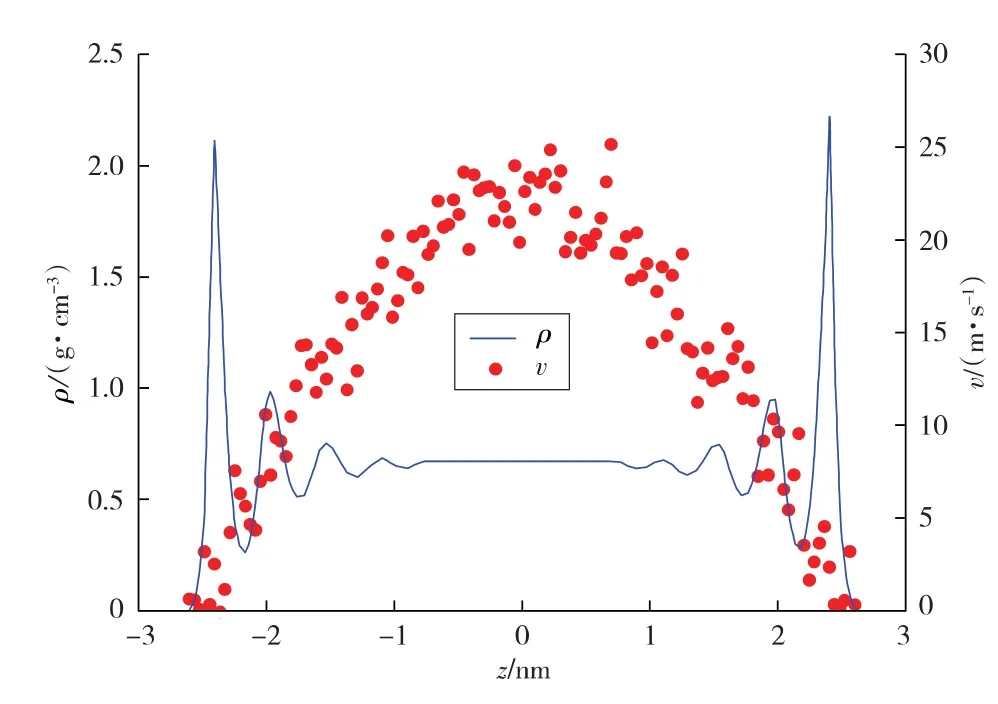
图2 方解石孔隙内的速度与密度分布

图2还展示了驱动力为5.2×10-14N时，正辛烷在5.24 nm的方解石孔隙内流动时的速度剖面。可以发现，烷烃的流速分布在整个孔隙空间内呈现抛物线形状，这与烷烃在有机质孔隙内的柱塞状流动特征截然不同［12］。因此，为了清楚认识页岩储层内原油的流动规律，有必要将有机质孔隙和无机质孔隙分别进行研究。为了进一步对孔隙内正辛烷的流动规律进行定量表征，采用考虑滑移的Poiseuille方程［12］对其速度剖面进行拟合，并计算得到方解石孔隙内的滑移长度：

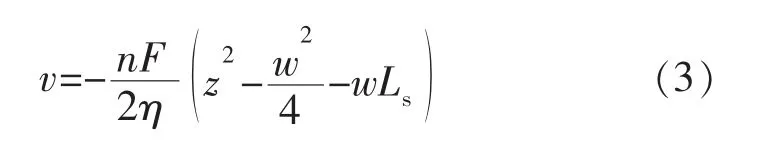
式中：n为孔隙内被驱动原子的数密度，1/m3；F为驱动力，N；η 为流体的有效黏度，Pa·s；w 为孔隙宽度，m；Ls为滑移长度，m。

图3展示了宽度为5.24 nm的方解石孔隙内正辛烷流动速度剖面的拟合结果。分别采用无滑移的Poiseuille方程和滑移方程（见式（3））对分子模拟的速度剖面进行拟合，可以发现，考虑滑移后的拟合方程为

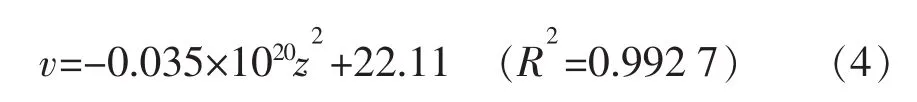
而不考虑滑移后的拟合方程为

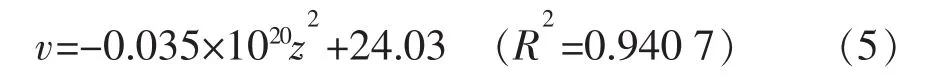
式中：R为相关系数。

研究表明，滑移方程的拟合效果更好，正辛烷在方解石孔隙内流动时存在滑移。在拟合所得到的速度剖面上，从固体表面外推到速度为0的距离即为滑移长度Ls。由图3可知，方解石孔隙内烷烃的滑移长度为-0.12 nm。滑移长度为负值，表明方解石孔隙内正辛烷的流动比无滑移Poiseuille方程的计算结果慢，固体壁面附近的烷烃分子不能流动。

图3 方解石孔隙内正辛烷流动速度剖面的拟合

3 不同矿物孔隙内正辛烷的流动规律

本文进一步分析了石英、有机质和方解石孔隙内烷烃流动规律的差异。图4a对比了不同矿物孔隙内正辛烷的密度剖面（353 K，30 MPa），各孔隙的尺寸均为5.24 nm。可以看出，有机质孔隙与石英和方解石孔隙内烷烃的密度剖面特征相近：壁面处，烷烃形成多层吸附，孔隙中央处为游离相（密度趋于定值）。造成该现象的原因在于，纳米受限空间内壁面与流体的相互作用对流体的赋存状态和流动规律具有显著影响。靠近固体壁面处，烷烃与壁面的相互作用较强，因此大量烷烃分子聚集在壁面附近，形成较高的吸附峰；逐渐远离固体壁面，壁面对烷烃分子的作用力减弱，其影响逐渐忽略不计，因此孔隙中央处密度几乎保持不变。图4a同样表明，有机质孔隙内烷烃的吸附峰值大于石英和方解石孔隙，说明有机质与烷烃的相互作用力更强，因此，与无机矿物孔隙相比，烷烃更倾向于聚集在有机质表面。

对于不同矿物孔隙内的烷烃分子，施加驱动力以研究给定压力梯度下烷烃的流动规律。图4b描绘了给定压力梯度条件下不同矿物孔隙内正辛烷流动的速度剖面（353 K，30 MPa）。其中有机质孔隙内烷烃受到的驱动力为1.04×10-14N，而石英和方解石孔隙内的驱动力为有机质孔隙的5倍，即5.2×10-14N。尽管有机质孔隙内烷烃受到的驱动力小于石英和方解石孔隙，但有机质孔隙内烷烃的流动速度却是最大的，其次为石英孔隙，方解石孔隙内正辛烷流动得最慢。此外，速度剖面形状也具有较大差别：有机质孔隙内速度（vor）剖面呈现柱塞状，而无机质孔隙内速度（vinor）剖面为抛物线形状。分别对各孔隙内正辛烷流动的速度剖面进行拟合，可以发现，利用滑移方程拟合烷烃在纳米孔内的速度剖面均得到了很好的效果（见图4b）。

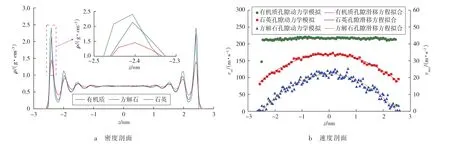
图4 不同矿物孔隙内正辛烷流动的密度剖面与速度剖面对比

根据图4b中的速度剖面计算了不同矿物孔隙内烷烃的滑移长度（见图5）。

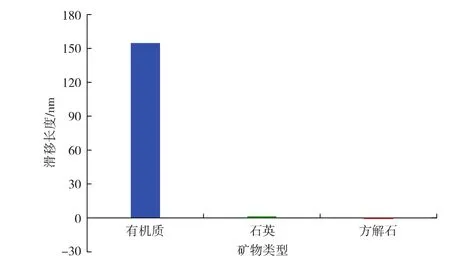
图5 不同矿物孔隙内正辛烷流动的滑移长度对比

由图5可见，滑移长度由大到小的顺序依次为有机质、石英、方解石。其中：有机质和石英孔隙内正辛烷的滑移长度为正值，表明正辛烷在有机质和石英孔隙内流动时的速度大于Poiseuille方程的计算结果，存在流动增强现象；但方解石孔隙内正辛烷的滑移长度为负值，表明部分烷烃分子吸附于方解石表面上无法移动，驱动力尚不足以完全克服方解石对正辛烷的吸引力，因此正辛烷在方解石孔隙内流动时的速度略慢于Poiseuille方程的计算结果。石墨烯纳米孔隙内流体的快速流动已被大量的实验和模拟结果证实，其主要原因为石墨烯表面的超光滑性使得流体流动的阻力非常小［25］，而方解石与石英壁面更粗糙，因此依然呈现抛物线形状的速度剖面。由于正辛烷与方解石之间的相互作用比石英的更强，因此，正辛烷在方解石孔隙内流动时所受到的阻力更大，流动更慢。综合以上分析可知，有机质孔隙中烷烃的流动速度最快。在现场实际页岩油开发中，应选择有机碳含量较高的地区进行打井，原油的可流动性更好，油井产量更高。

4 结论

1）在页岩纳米孔内，受液体与固体之间强相互作用的影响，正辛烷在靠近固体壁面处形成多层吸附，但在孔隙中央为游离相。有机质与烷烃的相互作用力更强，因此，有机质孔隙内烷烃的吸附密度高于石英和方解石孔隙。

2）由于石墨烯壁面具有超光滑性，因此烷烃的流动呈现柱塞状；但在石英和方解石孔隙内，烷烃流动的速度剖面为抛物线形式。孔隙内的速度剖面可以用考虑滑移的Poiseuille方程进行描述。

3）有机质孔隙内正辛烷的流动速度最快，石英次之，方解石最慢。在有机质和石英孔隙内，正辛烷的滑移长度为正值，但方解石孔隙内，部分烷烃分子吸附于固体表面无法移动，因此滑移长度为负值。