基于人工神经网络和地层剥蚀原理的地应力场反演研究

马玉岩，沈 阳，侯东奇

（中国电建集团成都勘测设计研究院有限公司，四川成都 611130）

0 前 言

人们认识地应力的历史只有近百年，对大型地下工程而言，初始地应力场的特征和分布规律对设计和施工都非常重要，目前最为有效的分析模式是考虑工程区域的地形、地质的特点，以现场地应力实测数据为依据，采用理论或数值分析的方法进行反演、回归和模拟，得到初始地应力场分布规律与量值。

付成华等（2006）［1］以溪洛渡水电站为例，依据地应力的实测资料，利用多元线性回归方法、神经网络方法和遗传算法，采用有限单元法求得整个坝区的初始地应力场。袁风波（2007）［2］以黄河拉西瓦水电站为例，根据“反演正算”原理，研究并提出了河谷区高地应力场的一种非线性反演方法。景锋等（2011）［3］总结了常用原位地应力测量法及工程区初始地应力场分析研究方面所取得的进展。王成虎（2014）［4］总结了广泛应用的26种地应力测试方法、基本力学原理及发展史。王金安、李飞（2015）［5］总结了国内外学者在地应力反演算法和工程运用中作出的改进和创新，提出了替代模型加速优化算法。张社荣等（2017）［6］以黄登水电站为例，分别采用传统多元线性回归方法、人工神经网络方法与考虑地质历史过程的基于逐步回归原理耦合人工神经网络的非线性智能方法，获得厂址区域的地应力场。蒙伟等（2021）［7］以斑竹林隧道为例，分别应用声值法检验、F检验、f检验反演岩体初始地应力场，验证了所采用回归模型和系数的可靠性。

本文以地处雅砻江地形急剧变化地带的两河口电站工程为例，基于人工神经网络（ANN）和地层剥蚀原理对其厂区地应力场的进行非线性反演研究，并通过现场探洞围岩破坏、区域构造背景分析等对反演成果的可靠性进行验证。

1 工程概况

两河口水电站是雅砻江中下游的“龙头”水库，位于四川省甘孜州雅江县境内，引水发电系统布置于雅砻江干流右岸山体中，厂房内共布置有6台水轮发电机组，总装机3 000 MW，其建筑物包括主厂房、副厂房、主变室、出线洞、通风洞、交通洞、排水廊道和开关站等，为大型地下洞室群。

两河口水电站所处的雅砻江、鲜水河及其支流河谷狭窄、谷坡陡峻，谷肩相对高差达500～1 000 m，厂址区域地形陡峻，为典型的高山峡谷地貌。工程区位于鲜水河-安宁河-则木河-小江断裂带和金沙江-红河断裂带所围限的“川滇巨型菱形断块”内，由鲜水河断裂带、玉农希断裂带、理塘-德巫断裂带、甘孜-理塘断裂带所围限的次级断块“雅江-理塘菱形断块”中部历史上经历过复杂的多次构造内动力地质过程，新生代后受到过强烈的外动力地质作用，岩体内部应力场较为复杂。

厂区地下洞室群布置于T3lh1（4）层～T3lh2（2）层坚硬的砂板岩中，岩体微风化-新鲜，以Ⅲ1类围岩为主，部分Ⅲ2类。厂区水平埋深约350～700 m，垂直埋深400～450 m，厂房纵轴线方位为NE3°。厂区主要发育有F9、F10、F11断层和节理裂隙等地质构造，地下水不发育。厂区实测最大主应力σ1为18.09～30.44 MPa，平均21.5 MPa，方向区间为N20.3°～57.7°E，平均N41.9°E，倾向坡外，略缓于岸坡。

2 计算原理

2.1 人工神经网络基本原理与算法

人工神经网络技术的核心是模拟人脑的知识获取和组织过程，目前应用最广泛也是发展最成熟的BP神经网络，它是按层次结构构造的，其结构如图1所示，包括一个输入层、一个输出层和一个或多个隐含层，一层的神经元只与紧邻的上一层、下一层的各神经元连接。

图1 BP神经网络结构模型

如果输入层有n个神经元，输出层有m个神经元，则网络是从n维欧氏空间到m维欧氏空间的映射。BP算法是一种快速梯度下降的方法，通过调整连接权值、网络规模（包括n、m和隐含层神经元数）实现任意精度逼近任何非线性函数。

2.2 地应力场非线性反演方法

将反演地应力的边界条件与应力值之间的非线性关系用一组神经网络（n，h1，…，hp，m）描述如下：

式中，P=（p1，p2，…，pn）是神经网络的输入节点表达；D=（d1，d2，…，dn）是神经网络的输出节点表达；NN（n，h1，…，hp，m）是建立的多层神经网络结构，其中n，h1，…，hp，m为输入层Fx、隐含层F1、…、层隐含Fp和输出层Fy的节点数。

采用人工神经网络建立边界条件与工程区域实测点应力值间的映射关系，实施方法如下：

（1）建立有限差分计算模型，实现从边界条件到实测点应力值的正分析过程。

（2）按均匀设计原理构建边界条件参数组合表［8］。

（3）将步骤（2）生成的参数组合带入步骤（1）进行计算，得到相应的应力值样本。

（4）将步骤（2）与步骤（3）得到的地应力值和边界条件参数，分别作为输入向量和输出向量，通过遗传算法优化神经网络结构及连接权值，建立遗传神经网络。

（5）利用样本训练神经网络，并进行检验。

（6）网络结构和训练次数成熟时，将地应力实测值作为输入向量，通过神经网络获得输出向量，即可采用的边界条件。

（7）将上一步得到的可采用边界条件代入数值计算软件，通过一次正向计算获得区域地应力场。

2.3 地表剥蚀原理

在河谷形成过程中，随着地表侵蚀、河谷剥蚀等长期地质强烈的卸荷作用破坏了河谷形成前区域地应力场的相对平衡状态，导致岩体内应力、应变及能量调整，并达到新的平衡状态。因此，在高山峡谷区域的河谷地应力反演中，考虑地表剥蚀卸荷效应对准确获得区域地应力场是必要的。

为考虑地表剥蚀卸荷效应，作如下假定：

（1）假定远古时期地面是无起伏的平地，构造运动在远古时期完成；

（2）初始地应力场由岩体自重应力和区域地质构造运动引起的构造应力组成；

（3）现有地应力场是在远古初始地应力场基础上，经过长期的地形剥蚀、冲淘形成的。

为反映地表剥蚀和河流侵蚀下切作用，模拟获得河谷岸坡初始地应力场的分布，地应力反演时采用基于弹塑性计算的过程分层开挖形成河谷（如图2所示），计算中的分层剥蚀高度一般依据现今河谷残留阶地确定。

图2 考虑地表剥蚀河谷下切作用所加边界条件

其模拟过程主要有：

（1）考虑研究区域的地形、地质构造、地层介质不均匀性等自然因素，在现状地形的基础上，以计算范围最高点为基准形成远古平坦地形；

（2）通过修正容重的系数参变量获得自重应力，通过在计算区域施加位移边界形成构造应力；

（3）对岩体采用弹塑性本构模型，通过逐步开挖模拟实现地表剥蚀卸荷效应。

3 地应力场反演分析

3.1 三维数值计算模型

采用三维有限差分模型进行地应力场反演分析，计算模型的坐标原点选在主厂房机窝位置，模型坐标原点位于主变室与进场交通洞的交叉点。计算模型沿X轴和Y轴的计算范围分别为1 500 m和1 800 m，竖直方向从海拔2 000 m到山顶，其区域位置如图3所示。由于工程洞群区域远河流侧一定范围内无地形等高线数据，故建模时根据现场调研进行了简化补充，其地形如图4所示。

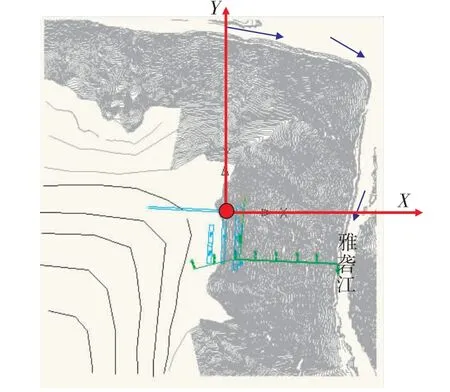
图3 数值计算模型区域示意

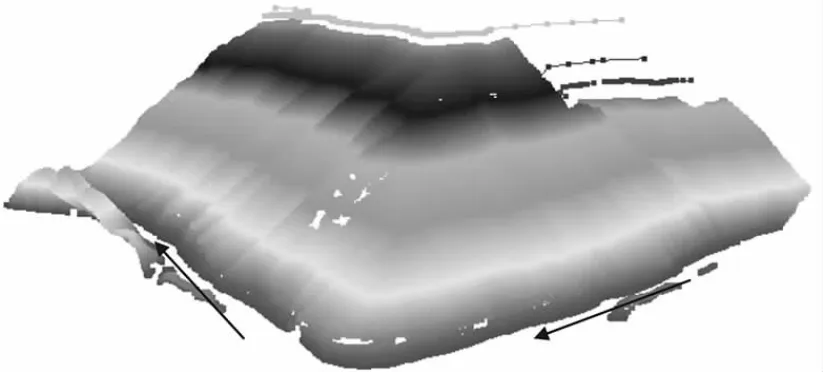
图4 模型中的厂址区地形起伏示意

根据地形图提供的地表等高线图，建立计算区域的三维模型如图5所示，共含有123.1万单元，27.5万节点。考虑到地应力反演的主要目的是获得厂区地应力分布特征，故模型中对厂房区域对其应力场和洞室稳定性影响显著的f3、f9、f10、f12、f25等条断层采用实体单元，同时考虑了厂址区域等地层。

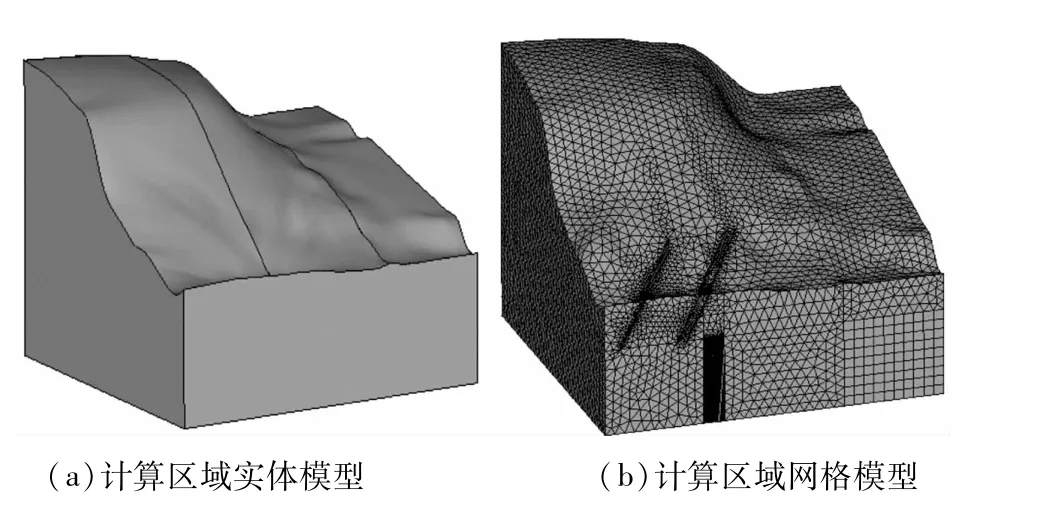
图5 三维计算模型

此外为验证地应力反演结果的合理性，模型中还包含有厂区探洞PD12和上支洞，如图6所示。为考虑地层剥蚀效应，模型还考虑了雅砻江“V”型河谷形成过程的剥蚀阶地，如图7所示。

图6 厂区探洞

图7 考虑地层剥蚀的三维模型

3.2 岩体本构模型与参数

两河口厂址区PD12和PD12上支洞调查揭示工程区主要出露地层为T3hl1（3）～T3hl1（5）和T3hl2（1）～T3hl2（3）层的变质砂岩、变质粉砂岩、粉砂质板岩等。岩石力学试验［9］调查表明，岩层各向异性系数（平行层理参数／垂直层理参数）为：干抗压强度0.70、湿抗压强度0.69、弹性模量1.07。可见该工程岩体的各项异性主要是强度的各项异性，而变形的各项异性一定程度上不十分明显。因此，地应力反演分层采用的是考虑层状结构面分布的层状岩体弹塑性力学模型。

两河口水电站厂址区域雅砻江深切河谷岸坡是远古地表受地表剥蚀和河流侵蚀下切及地质构造运动综合作用的结果，岸坡岩体经历了不同程度的卸荷作用过程，此过程伴随着岩体发生不同程度的弹塑性变形，在该过程中岩体可能出现压剪和张拉破坏。故计算中采用考虑岩体和层面分别屈服的莫尔—库仑与拉破坏准则结合的复合准则，模拟这种外动力作用导致浅层层状岩体不可恢复的变形。计算过程中的岩体力学参数取值见表1～2。

表1 岩体变形参数建议值［9］

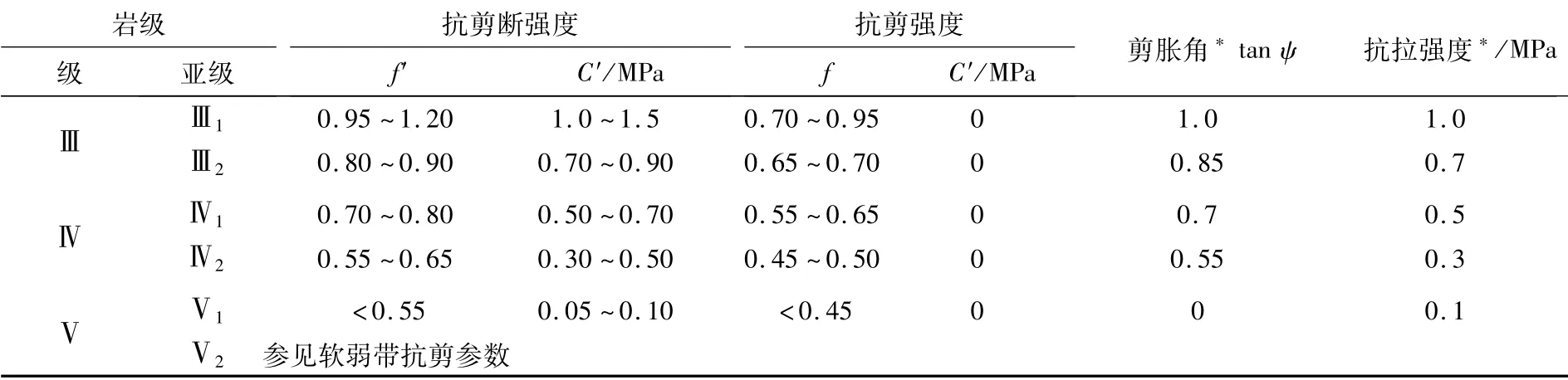
表2 岩体强度参数建议值［9］

3.3 地应力场非线性反演计算

3.3.1计算工况

首先将实测地应力数据的主应力与主应力方向转换到计算坐标下的6个应力分量值。通过多方案的三维数值试算比较与各种构造因素的敏感性回归分析表明：Z-Y面上竖直剪切构造因素和Z-X面上竖直剪切构造因素不明显，而自重和其他构造因素作用显著，最后确定地应力场形成的构造模式为：①自重、②X向挤压构造、③Y向挤压构造、④水平X向剪切构造、⑤水平Y向剪切构造（水平X向剪切=水平Y向剪切）。

3.3.2 基于均匀设计的样本构造

以“反演正算”的思路进行两河口厂址区域的地应力场的非线性反演。根据对两河口厂址区域模型的试算分析、实测地应力特征和工程地质分析，采用均匀设计方法将数值计算的位移边界条件和重力修正系数共5个参数各分为5个水平（见表3），由此构造了30组学习训练样本试验组合方案，并另外构造了5组测试样本用于测试网络预测效果，如表4所示。

表3 样本水平设计

表4 神经网络测试样本

3.3.3计算过程及结果

将以上边界条件各组样本方案代入FLAC 3D进行计算，获得每个样本的应力计算值作为神经网络学习训练的输入值，将设定的边界条件作为对应输出值，建立测点应力分量和边界条件非线性映射关系的进化神经网络模型。在这一过程中，采用遗传算法优化神经网络的最佳网络结构和连接权值。经计算得到的神经网络的最佳网络结构为30-48-13-5，即：输入层为30个节点，中间隐含层为两层，第一隐含层的节点数为48，传递函数tansig；第二隐含层的节点数为13，传递函数logsig；最后输出层为5个节点，传递函数purelin。利用该训练好的进化神经网络模型，输入各个测点的实测应力分量值，得到了地应力场的位移边界条件和重力修正系数，如表5所示。

表5 由进化神经网络得到的位移边界条件和重力修正系数

利用非线性回归反演得到的边界条件进行有限差分正算，并由此获得了两河口水电站厂址区域地应力场的分布特征，统计分析可知协方差Q=61.2，复相关系数R=0.952，表明从反演结果本身来看本次反演有效。

3.4 地应力反演结果检验分析

各测点处的地应力的计算结果与实测值之间的对比关系如表6所示。从这些非线性回归反演的结果可以看出，非线性回归反演结果与实测的地应力在规律上保持一致性，三个方向的正应力相对误差均约为13.9%，数值吻合较好。

表6 实测地应力与回归计算地应力对比 单位：MPa

对比分析反演计算模型中PD12探洞和PD12-上支洞的计算围岩破坏特征与现场探洞围岩实际破坏特征可见，两者总体也较为一致，分别如图8～9所示。计算结果显示探洞PD12左侧墙脚区破坏接近度较大，这实际上是因为探洞PD12（探洞轴线近EW向）左侧边墙岩体为反倾层面，在厂区岩体初始地应力为NE向作用下产生层状岩体的结构—应力型破坏，与现场围岩的实际破坏基本吻合。对PD12-上支洞，计算结果显示探洞近河谷侧顶拱破坏接近度较大，与现场实际的临河谷侧产生应力型片帮剥落现象较为一致。

图8 地应力反演模型中厂址区PD12围岩结构-应力型破坏与现场实际对比

通过上述测点位置实测地应力值与反演值的对比、现场探洞围岩应力型破坏特征与地应力反演计算模型中探洞破坏特征对比验证可见，总体上来说，本次反演得到的地应力场分布结果是合理的，这也证实了进化神经网络在地应力场非线性反演中具有优越性。

图9 地应力反演模型中厂址区PD12-上支洞围岩应力型破坏与现场实际对比

4 结 论

（1）基于人工神经网络（ANN）的非线性反演研究方法能够考虑多种地质构造运动的荷载或位移作用模式和自重的影响，更好地建立实测地应力值与模型边界条件的非线性映射关系。

（2）从地质演化的角度来看，两河口厂址区域地应力场是在远古构造应力场的基础上，随着深切河谷形成过程中强烈的侵蚀、剥蚀和冲淘等地质作用下和长期卸荷的结果。考虑地层剥蚀卸荷效应对于正确认识和评估区域地应力场的应力分布和状态是非常有必要的。

（3）通过现场探洞围岩破坏、区域构造背景分析等对反演成果的可靠性进行验证。本次反演得到的地应力场分布结果是合理的，基于人工神经网络和地层剥蚀原理的地应力反演方法适用于河谷地应力场。