基于线性储能规律的红砂岩蠕变能量演化分析方法
刘之喜,赵光明,孟祥瑞,张若飞,程详,董春亮,黄顺杰
(1.安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室,安徽淮南,232001;2.安徽理工大学煤矿安全高效开采省部共建教育部重点实验室,安徽淮南,232001;3.安徽理工大学地质资源与地质工程博士后流动站,安徽淮南,232001;4.淮北矿业股份有限公司博士后科研工作站,安徽淮北,235000;5.安徽理工大学力学与光电物理学院,安徽淮南,232001)
砂岩在采矿工程中普遍存在,具有弹塑性特征,蠕变作为其重要的力学特性,是巷道支护中需要考虑的重要因素之一。巷道围岩受长期荷载的影响会发生蠕变失稳现象,为了研究巷道围岩蠕变失稳破坏规律,人们提出了大量的蠕变模型来模拟岩石的蠕变行为,其中,Burgers和Nishihara 等模型被广泛地应用于采矿工程岩石蠕变本构模型的研究中[1−2]。岩石的蠕变本构研究主要采用非线性理论推导岩石蠕变本构方程[3−8],蠕变方程参数的确定非常困难,因为参数通常不是常数,是与蠕变时间和蠕变应力有关的变量,参数的物理意义通常并不明确,所以,由蠕变的应力−应变−时间建立岩石的本构方程及强度理论必将导致分析结果的不确定性。热力学认为,物质受外部因素影响其尺寸、形状、密度等物理变化都是岩石内部能量转换与外界能量交换的结果,岩石破坏从热力学角度可以解释为能量驱动下的状态失稳现象[9−12],故从该角度研究岩石破坏,从而建立以能量变化为判断依据的破坏准则,能够更好地揭示岩石破坏规律。
关于岩石能量演化的研究,杨磊等[13]通过单轴循环加卸载研究了煤岩体的能量演化规律和破坏机制发现煤岩体的能量密度随轴向荷载增加呈非线性增长,并且岩石的破坏主要是由于到达储能极限时,弹性能释放引发岩石的张拉破坏。孟庆彬等[14]利用MTS对岩石进行了6种围压下的循环加卸载试验发现能耗比能够表征岩石内部损伤积累状态,并且围压对能够抑制岩石峰后的能量耗散。王桂林等[15]进行了单轴压缩下节理砂岩能量演化机制倾角效应的试验研究,对峰前与峰后总能量的研究发现岩体发生失稳破坏,其难易程度为“难—易—难”的变化趋势。李江腾等[16]利用RYL-600剪切流变仪对岩石进行了单轴循环加卸载试验发现塑性耗散能在循环初期较大,后逐渐减保持稳定,临近破坏时耗散能为破坏前的4倍左右。宫凤强等[17−19]在考虑岩石加载全过程中能耗特性的基础上,得到了线性储能规律,改进了峰值能量冲击性指数的计算公式,进而建立一种基于剩余弹性能指数(峰前弹性能密度和峰后破坏能密度的差值)的岩爆倾向性判据;并在对不同岩石的能量研究中提出了耗散能与弹性能的线性关系,发现在岩石峰值抗压强度下,弹性能量密度与耗散能量密度的比值趋于恒定;此外,在基于线性储能规律的基础上提出了峰值强度储能指标用来估计和分类岩石的岩爆倾向。关于岩石蠕变能量的研究,韩超等[20]利用砂岩单轴分级加卸载蠕变试验,总结了岩石破坏的能量演化规律,认为衰减能量系数随应力水平增长呈幂函数形式降低,从而提出了一种可以有效预测破坏应力的方法。瞿明磊等[21]进行了岩石剪切加载−蠕变−卸载的研究,分析了剪切蠕变过程中滞回面积和循环级数的关系、循环剪切加载和蠕变结束时的累积变形的演化特征,认为塑性变形能与循环级数和法向载荷呈正相关。
上述关于蠕变能量演化的研究通常采用加载—蠕变—卸载的试验方法对岩石进行能量演化分析,虽然能够得到岩石分级加卸载蠕变的能量演化规律,但缺少单轴分级加载蠕变试验能量演化规律的研究。本文根据应力相同时单轴分级蠕变和单轴循环加卸载都产生了比单轴压缩更大的变形这一共性,通过单轴循环加卸载试验来探寻红砂岩的能量演化特征。岩石蠕变能量演化分析方法的研究有助于探索岩石蠕变过程中能量演化规律,进而对巷道失稳时间预测、失稳方式预测、二次支护时机选择等研究起到指导作用。通过单轴蠕变试验、单轴分级加卸载试验以及蠕变后的单轴循环加卸载试验探索红砂岩蠕变过程中能量演化特性,获得蠕变的弹性能及耗散能与时间和应力的关系,研究结果对巷道宏观结构蠕变演化与失稳机理、二次支护时机等方面课题具有积极意义。
1 岩石能量的计算方法及试验方案
1.1 能量计算方法
假设在加卸载过程中岩石与外界没有热交换,即只有弹性能与耗散能[22−23],其中,弹性能在特定条件下具有可逆性,耗散能是单向的,岩石的总能量密度计算公式为[24]

式中:u为总能量密度;ud为耗散能密度;ue为储存在岩石内的弹性能密度。
图1所示为岩石在轴向荷载σ1时加卸载过程的应力−应变曲线。耗散能密度ud由加载与卸载曲线包围的面积确定;弹性能密度ue由卸载曲线下的面积确定。弹性能密度ue与耗散能密度ud计算公式为[24]:
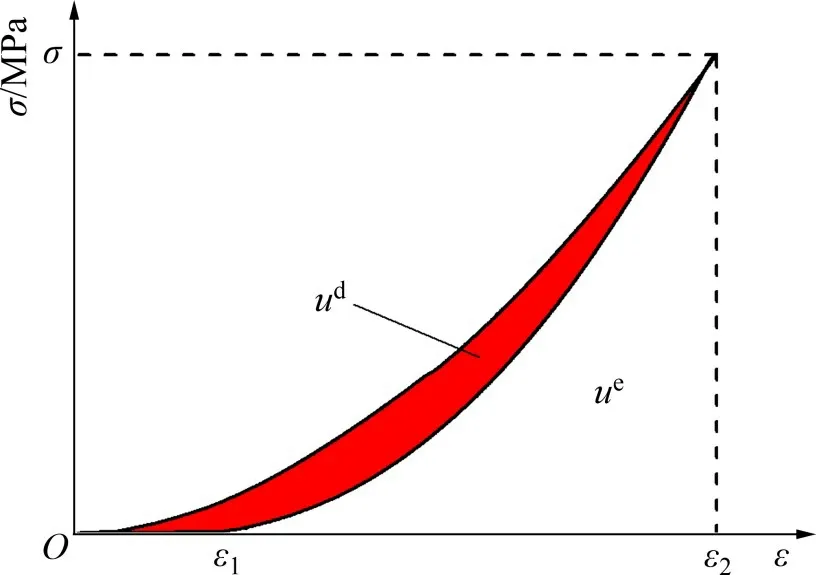
图1 岩石加卸载的能量密度示意图Fig.1 Schematic diagram of energy density for rock loading and unloading

1.2 蠕变试验方法
蠕变试验采用的红砂岩试件为同一产地,其内部结构相似。采用试验室机器将红砂岩切割打磨成国际岩石力学要求的标准尺寸(高100 mm,直径50 mm)圆柱体。单轴抗压强度试验、单轴压缩试验、单轴分级蠕变试验、单轴循环加卸载试验、蠕变后的单轴循环加卸载试验均在电子万能试验机DDL-200 上进行,其最大荷载为200 kN。试验测得红砂岩试件的单轴抗压强度约为47.7 MPa。破坏前后红砂岩试样如图2所示。

图2 破坏前后红砂岩试件Fig.2 Red sandstone specimens destroyed
单轴蠕变试验采用分级蠕变直至试件破坏,各级蠕变的初始应力设置为5 MPa,每级应力增加幅度为5 MPa,共9级加载,各级蠕变应力之间的加载速率设为0.25 MPa/s,每级蠕变时间为10 h。根据单轴蠕变试验,可得红砂岩单轴蠕变的应变−时间曲线,从蠕变应变−时间曲线可以将岩石试样的蠕变分成3 个阶段:衰减蠕变、匀速蠕变、加速蠕变。在衰减蠕变阶段,蠕变速率不断减小;在匀速蠕变阶段,蠕变速率基本保持不变;在加速蠕变阶段,蠕变速率快速增长阶段。在单轴分级蠕变试验中,前8个分级蠕变阶段都存在衰减与匀速阶段,最后一级蠕变阶段存在明显的加速蠕变。在加速蠕变阶段,红砂岩试件应变速率随着时间也逐渐增大。为了便于区分岩石蠕变试验3个阶段特征,将红砂岩应变−时间曲线中包含衰减蠕变、均匀速蠕变以及加速蠕变的第九级蠕变进行局部放大,第九级加载(加载应力45 MPa)蠕变应变−时间曲线如图3所示。从图3可见:在45 MPa 荷载作用下,约4 h后红砂岩进入加速蠕变阶段,加速蠕变持续2 h 左右试样破坏,试验机停止试验。从微观角度可以将岩石蠕变分为张开裂隙逐渐闭合、岩石软弱部分与坚硬部分进行位置调整以及岩石试样破裂3个阶段[25]。
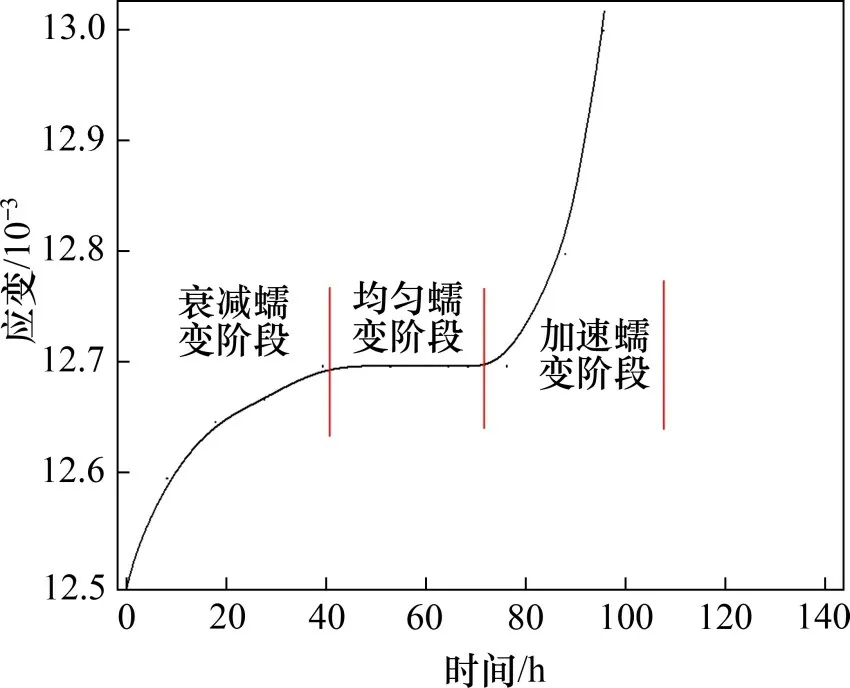
图3 第九级加载蠕变应变−时间曲线Fig.3 The 9th-order of creep strain−time curves
2 红砂岩蠕变过程中的能量演化
单轴分级蠕变应力−应变曲线如图4所示。从图4可见应变随应力增大呈阶梯式上升。基于1.1节能量计算方法能够得出蠕变的总能量密度,但是不能得出蠕变的弹性能密度与耗散能密度。红砂岩蠕变试验各应力处的弹性能密度与耗散能密度对蠕变破坏本质的研究具有积极意义,而且单轴分级蠕变与单轴循环加卸载存在一定的相似之处,即在应力相等时都比单轴压缩产生了更大的变形,因此,可以利用分析单轴循环加卸载的能量演化,探索红砂岩蠕变的能量演化规律。

图4 单轴分级蠕变应力−应变曲线Fig.4 Stress−strain curves of uniaxial creep
2.1 单轴循环加卸载能量演化
单轴循环加载试验共分9组,其循环加卸载应力上限分别为5,10,15,20,25,30,35,40和45 MPa,应力下限均为0 MPa,循环次数均为20次,加载应力为0.25 MPa/s,每组试件循环20次。图5所示为应力上限为5 MPa的循环加卸载应力路径。

图5 应力上限为5 MPa的单轴循环加卸载应力路径Fig.5 Uniaxial cyclic loading and unloading stress path under 5 MPa of stress
图6所示为应力上限15,30和45 MPa 时循环加卸载应力−应变曲线。从图6可见:单轴循环加卸载的应力上限越大,加卸载产生的应变越大。红砂岩单轴循环加卸载曲线整体上呈非线性特征,存在明显的滞回效应。加卸载试验的应力−应变曲线路径均低于前一次加载的应力−应变曲线路径,随着加卸载次数增加,应力−应变曲线的位置逐渐向右移动。这是因为岩石并非通常假设的匀质体,其内部存在许多细微的原生微裂纹、微裂隙等缺陷,红砂岩在循环荷载的反复加卸载作用下内部的原生微裂隙相邻界面的摩擦阻力逐渐减小,原生微裂隙逐渐被压密,红砂岩的变形不断累积而使应力−应变曲线逐渐右移。
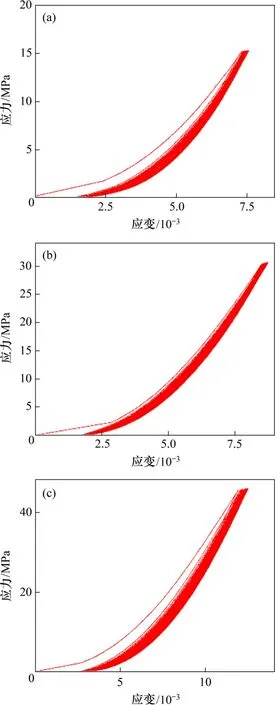
图6 应力上限为15,30和45 MPa的单轴循环加卸载应力−应变曲线Fig.6 Uniaxial cyclic loading and unloading stress−strain curves with stress upper limits of 15 MPa,30 MPa and 45 MPa
循环稳定后,红砂岩内部的残余变形逐渐减小,直到某次循环不再产生残余变形,红砂岩的加载曲线与卸载曲线形成一个密闭的滞回环。红砂岩的加卸载过程中形成的密闭滞回环如图7所示。

图7 非线性伪弹性体应力−应变曲线Fig.7 Stress−strain curves of nonlinear pseudo-elasticity
根据非线性黏弹性理论,无残余变形的红砂岩为非线性伪弹性体。所谓非线性伪弹性体是指在承受循环荷载时应变不随外加应力同时回到原点,应变有滞后现象[26]。当应力上限为15 MPa和20 MPa 时,约在10 次循环出现非线性伪弹性体;当应力上限为25,30和35 MPa时,约在14次循环出现非线性伪弹性体;当应力上限为40 MPa和45 MPa 时,约在17 次循环出现非线性伪弹性体。从能量角度来看,非线性伪弹性体在加卸载过程中只有弹性能密度与滞回效应耗散能密度。滞回效应耗散能密度是由于滞回效应存在而产生的耗散能[10]。红砂岩内部原生微裂隙被压密后变为非线性伪弹性体,继续承受循环加卸载作用时,再次出现残余变形,此时,循环加卸载应力−应变曲线位置再次向右逐渐移动。因此,循环荷载作用下红砂岩的残余变形规律可以归纳为:存在较大的初始残余变形—无残余变形—再次出现残余变形。通过对岩石在循环加卸载的研究发现:岩石在承受加卸载作用后出现“硬化”即峰值强度变大现象[27−29],在反复加卸载作用下峰值强度降[30−31]。结合尤明庆等[28]对大理石循环加载硬化作用分析,可以认为循环荷载作用后岩石的峰值强度改变的主要原因有以下2个方面:一方面,与岩石循环次数有关,在相对较少的加卸载次数作用下只是将岩石内部的微裂隙压密,岩石被压密后其峰值强度增大,当加卸载次数达到一定值时,岩石有新裂纹萌生和旧裂纹扩展,致使峰值强度降低;另一方面,与岩石内部微小颗粒的排列、胶结或结晶结构方式具有相关性,不同岩性的岩石其试验结果也会产生差异。
在单轴循环加卸载中,加载过程是输入能量的过程,输入的能量一部分被耗散,为耗散能;另一部分为弹性能储存在岩石内部,在特定条件下具有可逆性。通过计算可得红砂岩试件在单轴循环荷载作用下的能量密度演化趋势。循环荷载作用下红砂岩耗散能的演化趋势如图8(a)所示。从图8(a)可以看出:初次加卸载产生的耗散能密度远大于其他循环次数产生的耗散能密度,在不同应力上限时,耗散能密度具有相同的演化趋势,即耗散能密度随着加卸载次数增多逐渐减小;当应力上限为5 MPa和10 MPa 时,约在5 次循环时耗散能密度下降趋势明显降低,逐渐趋于稳定;当应力上限为15 MPa和20 MPa 时,约在循环10 次时出现耗散能密度下降趋势降低;循环10 次后,随着循环次数增多,耗散能密度存在较小幅值波动;当应力上限为25,30和35 MPa时,约在14次循环时耗散能密度下降趋势明显减小;14 次循环后,岩红砂岩下降趋势不明显,耗散能密度整体呈较小的波动;当应力上限为40 MPa和45 MPa时,在17次循环时出现耗散能密度下降趋势减缓,耗散能密度趋于稳定。可知:非线性伪弹性体出现的循环次数与耗散能密度下降趋于稳定后的循环次数基本保持一致。
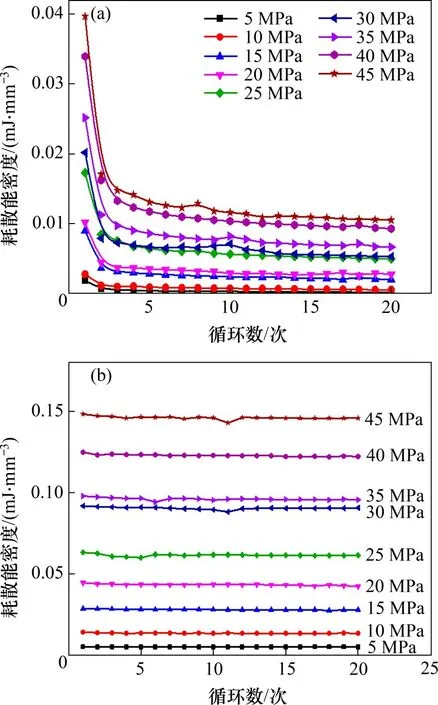
图8 能量密度−循环次数曲线Fig.8 Energy density−cycle number curves
红砂岩试件的弹性能密度随着循环次数增加的演化趋势如图8(b)所示。从图8(b)可见:循环加卸载的应力越大,岩石储存的弹性能密度越大;同时,岩石的弹性能波动幅值也越大。当应力上限为25 MPa 时,第5 次循环的弹性能密度与首次加卸载的相差0.001 9 mJ/mm3,下降了约3%;当应力上限为30 MPa时,第11次循环产生的弹性能密度与首次加卸载的相比下降了0.002 6 mJ/mm3,下降了约2.81%;当应力上限为35 MPa时,第7次加卸载产生的弹性能密度与首次加卸载的相差0.291 mJ/mm3,下降了约2.97%;当应力上限为45 MPa时,第11次加载储存的弹性能密度与首次加卸载的相差0.004 1 mJ/mm3,下降了约2.76%;在加卸载过程中,红砂岩的弹性能密度−应力曲线近似于与应力轴平行方向,在循环过程中存在一定程度的波动,但是弹性能密度波动的幅值与弹性能密度的比值最大为3%左右,弹性能密度变化幅度与弹性能密度相比可以忽略不计,因此,可以认为循环加卸载次数对岩石的弹性能密度无影响。
红砂岩的能量密度演化规律主要有:红砂岩的内部裂纹被压密后在加卸载作用下只存在弹性能与滞回效应能,在应力上限恒定的单轴循环加卸载作用下,红砂岩的弹性能密度基本保持不变。红砂岩单轴循环加卸载试验中,应力随时间而改变,而在同一级蠕变时,承受的外部荷载不随时间而改变,故利用红砂岩单轴循环加卸载曲线能量演化规律无法对红砂岩单轴分级蠕变的能量演化进行分析。根据单轴循环加卸载中红砂岩的弹性能密度基本保持不变这一特性,可以假设蠕变的长期荷载下红砂岩的弹性能密度基本保持不变。
2.2 红砂岩蠕变后在循环荷载作用下的能量演化
为了验证在蠕变的长期荷载作用下岩石的弹性能密度基本保持不变这一假设的正确性,设计蠕变后的单轴循环加卸载试验,分析岩石的弹性能密度演化规律。蠕变后的单轴循环加卸载试验共分9组,加载方案如表1所示,其中,单轴循环加卸载次数均为10次。在荷载为45 MPa时,经历6 h 左右的蠕变后试样已经发生破坏,因此,在该荷载下,进行蠕变时间为2 h的蠕变试验,再进行应力上限为45 MPa、下限为0 MPa 的单轴循环加卸载试验。蠕变后的单轴循环加卸载试验、单轴分级蠕变试验和单轴循环加卸载试验的加载速率均设为0.25 MPa/s。对蠕变后再进行单轴循环加卸载试验的红砂岩试件,无论是否破坏都不再重复使用。
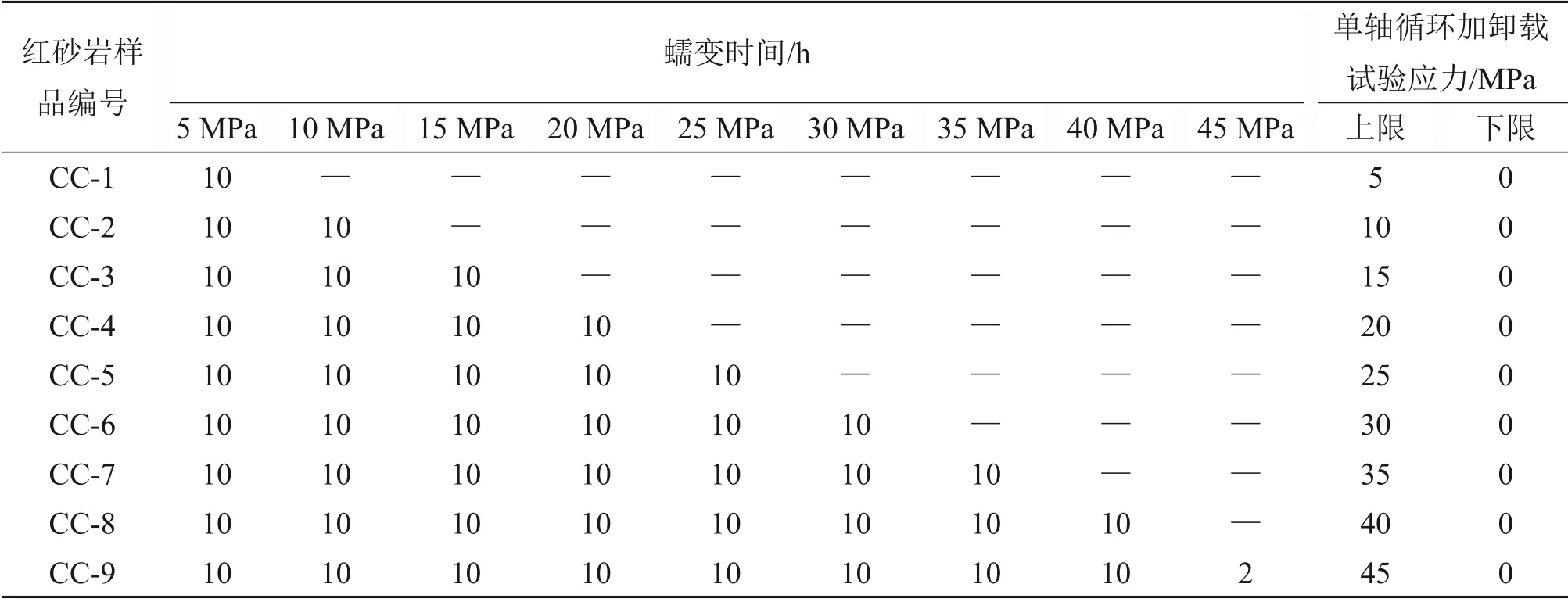
表1 蠕变后单轴循环加卸载试验方案Table 1 Tests for uniaxial cyclic unloading after creep
蠕变后的循环加卸载试验曲线如图9所示。从图9可以看出:在红砂岩蠕变后的单轴循环加卸载试验中,每次加卸载的应力−应曲线近似重合,但该曲线并非是一个密闭的滞回环,只是由于每次加卸载产生残余变形较小,应力−应变曲线位置向右移动不明显。

图9 蠕变后单轴循环加卸载应力−应变曲线Fig.9 Stress−Strain curves of uniaxial cyclic loading and unloading after creep
在分级蠕变荷载的作用下,红砂岩内部微裂隙逐渐被压,蠕变后继续承受循环加卸载的作用,岩石内部晶界产生损伤,蠕变后的单轴循环加卸载曲线向右移动不明显,说明蠕变后的循环加卸载试验对岩石内部晶界造成的损伤较小,红砂岩内部只有较少的新裂纹萌生,产生的残余变形较小。蠕变后的单轴循环加卸载应力−应变曲线整体上呈非线性特征,在循环荷载作用下,能量形式主要有弹性能、滞回效应耗散能以及极少量的由于塑性变形产生的塑性耗散能。
红砂岩单轴循环加卸载试验和蠕变后单轴循环加卸载试验的弹性能密度对比如图10所示。可见:从图10随着加卸载次数增多,弹性能密度变化曲线均近似与循环次数轴平行,弹性能密度基本保持不变。单轴循环加卸载的弹性能密度与蠕变后单轴循环加卸载的弹性能密度基本相同,并且蠕变后的单轴循环加卸载的弹性能密度随着加卸载次数增加波动幅度更小,说明被压密后,岩石的储能性质更稳定。蠕变后的弹性能演化规律验证了文中假设的正确性。
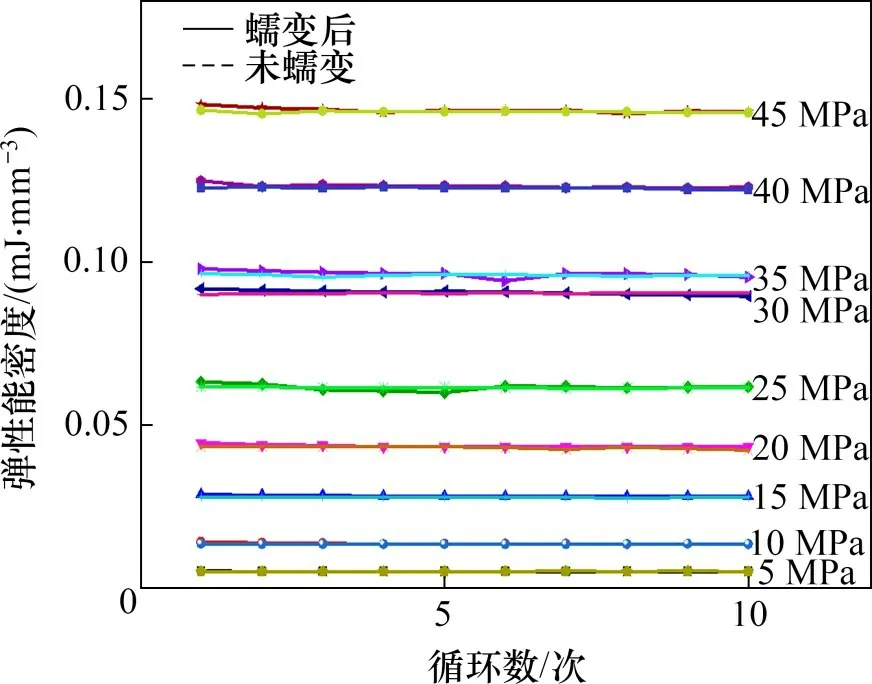
图10 红砂岩的弹性能密度对比Fig.10 Elastic energy density of red sandstone
3 红砂岩的线性储能规律
宫凤强等[17−19]研究表明弹性能密度与输入的总能量密度呈线性关系,为弹性能密度的计算提供了一个新思路。表2所示为红砂岩单轴循环加卸载试验的第一次加卸载产生的能量密度。由于本次试验的红砂岩具有相同的内部结构,故单轴循环加卸载第一次加卸载的各种能量密度应与单轴压缩相同应力处的能量密度相等。
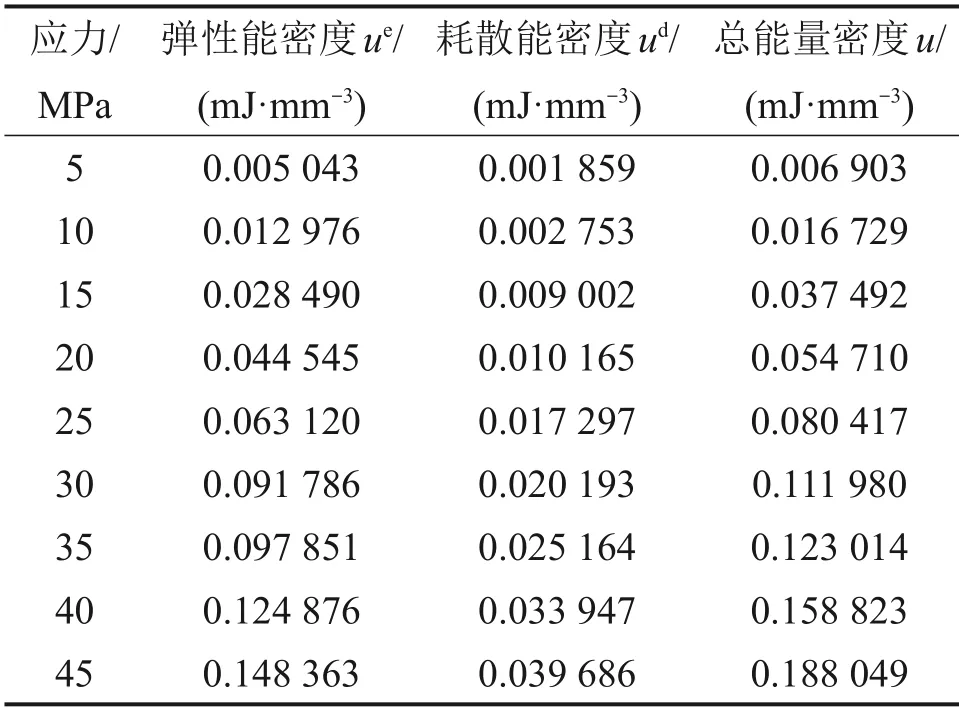
表2 红砂岩第一次加卸载的能量密度Table 2 Energy density of first loading and unloading of red sandstone
对红砂岩单轴循环加卸载首次加卸载产生的弹性能密度与总能量密度进行拟合,拟合校正系数R2为0.999 18,拟合曲线如图11所示,从图11可见:首次加卸载中的弹性能密度ue与总能量呈线性关系,与宫凤强等[17−19]提出的线性储能变化规律一致。

图11 弹性能密度−总能量密度拟合曲线Fig.11 Fitting curve of elastic energy density−total energy density
单轴循环加卸载试验的首次加卸载的弹性能量密度与总能量呈线性关系,并且在单轴循环加卸载作用下,红砂岩弹性能密度基本保持不变,因此,可以利用单轴压缩试验和单轴循环加卸载试验并结合红砂岩的线性储能规律确定红砂岩单轴压缩任意应力处的能量密度。蠕变的长期荷载对红砂岩的弹性能密度无影响,故当单轴压缩的应力与单轴分级蠕变的应力相等时,两者的弹性能也相等,从而,可进一步求得单轴分级蠕变任意应力处的弹性能密度与耗散能密度,得到一种岩石蠕变能量演化分析的新方法。
4 单轴分级蠕变能量演化
采用试样CC-10,CC-11和CC-12 进行单轴分级蠕变试验。红砂岩的能量密度离散程度较小,因此,试验结果采用多次测量结果的平均数。红砂岩单轴分级蠕变试验能量密度如表3所示。

表3 红砂岩单轴分级蠕变的能量密度平均值Table 3 Average energy density of uniaxial creep in red sandstone mJ/mm3
根据耗散能产生方式不同,耗散能ud可以分为加载耗散能udl与蠕变耗散能udc,其中,加载耗散能udl是指在单轴分级蠕变试验各级之间加载产生的耗散能,而蠕变耗散能udc是指在岩石在持续承受不变荷载时产生的耗散能。

单轴分级蠕变的弹性能密度以及蠕变产生的耗散能密度演化规律如图12所示。由图12可知:在单轴分级蠕变过程中,耗散能密度和弹性应变能密度均与轴向应力成正比,并且均呈非线性增长;蠕变产生的蠕变耗散能低于各分级加载过程中的加载耗散能,并且在整个蠕变过程中,弹性能量密度均大于加载耗散能密度以及蠕变耗散能密度。当蠕变的荷载水平逐级增大时,蠕变耗散能起初增长较为缓慢,在45 MPa 应力下,蠕变耗散能显著增大;在整个蠕变过程中,加载耗散能密度均高于蠕变耗散能密度;在45 MPa 应力下,蠕变耗散能约为0.025 25 mJ/mm3,与40 MPa 应力下,蠕变耗散能相比约增长79%。

图12 能量密度−应力的演化规律Fig.12 Evolution of energy density−stress
红砂岩能量密度−时间的演化规律如图13所示。从图13可见:红砂岩的弹性能密度随时间增大呈阶梯式增长,即每级蠕变时,弹性能基本保持不变;当任意级蠕变结束进入下一级蠕变时,岩石的轴向荷载增加,岩石的弹性能密度也随之增加;在蠕变过程中,耗散能密度也呈阶梯式增长,与弹性能密度变化不同的是,岩石耗散能密度在每一级蠕变时也有能量耗散,并且每级蠕变时产生的耗散能密度呈非线性增长,蠕变的级数越高,蠕变耗散能增长速率越快;临近破坏时,耗散能密度有显著的增长趋势;蠕变时,红砂岩内部的微裂隙逐渐被压密后,岩石逐渐硬化,当红砂岩受长期荷载时,红砂岩内部逐渐产生有新裂纹萌生,使岩石的承载有效面积减小,岩石的承载能力降低,致使岩石有更多的微裂纹萌生。裂纹之间相互连接产生更大的裂纹,随着时间的增长,当裂纹达到一定程度时,岩石的储能性降低,弹性能量开始释放,使红砂岩发生张拉破坏。
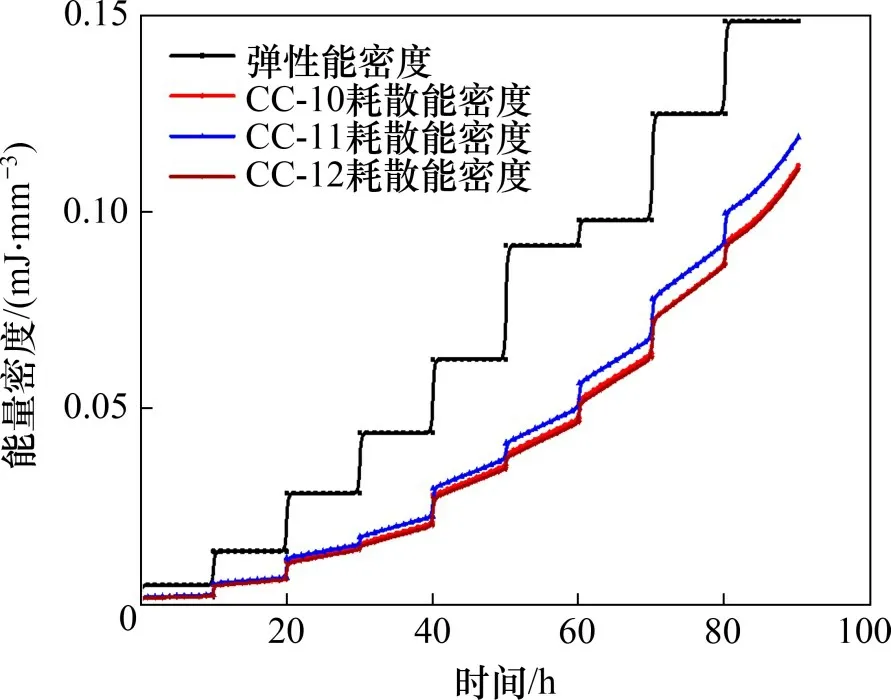
图13 能量密度−时间的演化规律Fig.13 Evolution of energy density−time
5 讨论
岩石并非通常假设的匀质体,内部存在许多天然的微裂纹,其强度存在一定的离散性。对蠕变进行研究时通常是对岩石蠕变的本构模型进行研究。由于岩石的离散性必然导致岩石本构模型参数的无规律变化及物理意义不明确,根据本构模型选用的参数会产生一定误差,对围岩蠕变的精确预测有一定的限制性。
岩石受外部荷载作用下往往伴随着能量积聚以及能量耗散[22−23]。应力上限恒定的单轴循环加卸载试验弹性能密度的研究结果表明:红砂岩在受循环加卸载或长期荷载作用下,弹性能密度基本保持不变。首先,模拟巷道围岩应力状态进行蠕变试验,得到岩石破坏时的总能量密度;然后,根据宫凤强等[17−19]提出的线性储能规律得到岩石弹性能密度,结合蠕变过程中弹性能密度不受长期荷载影响这一特性,得到巷道围岩的弹性能密度以及耗散能密度;再利用谢和平等[22]提出的能量积聚与释放的岩体强度整体破坏准则,有望获得一种比蠕变本构模型更精确的围岩蠕变失稳的预测方式。
外力对岩体做的功一部分转化为介质内的耗散能,使岩体强度逐步丧失[22]。在蠕变过程中,弹性能密度不受长期荷载的影响,随着蠕变时间增长,耗散能不断增大,岩体的强度降低,这意味着岩体储能极限降低,当岩体储能极限低于蠕变时的弹性能密度时,岩体的弹性释放,岩体发生失稳破坏。
在上述分析中不可忽视的因素是尺寸效应,不同尺寸下岩石的储能极限是否存在改变、不同尺寸下岩石的弹性能密度是否仍然不受循环荷载影响或蠕变的长期荷载影响,以及探索岩石在不同尺寸下蠕变耗散能对岩石峰值强度影响等,都有待进一步研究。
6 结论
1)在单轴循环加卸载作用下,岩石内部的微裂隙被压密,岩石成为非线性伪弹性体,即红砂岩只存在弹性变形,无残余变形,并且非线性伪弹性体只有弹性能密度与滞回效应能密度。
2)成为非线性弹性体后,红砂岩继续承受加卸载作用,内部会有新裂纹萌生旧裂纹扩展,再次产生残余变形,故在单轴循环加卸载作用下,红砂岩残余变形规律为:较大的初始残余变形—无残余变形—再次出现残余变形。
3)当单轴循环加卸载的耗散能达到初次平衡时,循环次数与循环加卸载过程中出现非线性伪弹性体的循环次数基本保持一致,并且在应力上限恒定的循环加卸载作用下,弹性能密度基本保持不变。
4)长期荷载对红砂岩的弹性能密度无影响,即在长期荷载作用下红砂岩的弹性能密度基本保持不变,并且红砂岩在蠕变后的单轴循环荷载作用下,弹性能密度与单轴循环加卸载的弹性能密度相比波动更小。
5)利用红砂岩线性储能规律和蠕变后红砂岩弹性能基本不变特性,可以得到蠕变的弹性能密度与耗散能密度,提出了一种岩石蠕变能量演化分析的新方法。

