集装箱码头失约集卡出口箱落箱位选择优化

尹延冬，靳志宏

(大连海事大学交通运输工程学院学院，大连 116026)

近年来，随着中国进出口贸易额持续增长，2020年集装箱吞吐量高达2.64亿标准箱，比2019年增长了1.2%。随着集装箱吞吐量的增长以及船舶大型化的发展，集装箱港口之间的竞争日趋激烈，在堆场空间资源有限的港口，只有扩建码头堆场空间或提高码头管理水平和作业效率才能提高港口的核心竞争力。然而在空间资源已经充分利用的码头堆场，扩建堆场并不现实。所以只有在现有空间资源的基础上，优化堆存方案，提高堆场作业效率，才能提高港口的核心竞争力。在集装箱港口中，经常出现集卡在某一时间段内集中到达的情况，并因此会造成码头拥挤排队、等待集卡尾气排放增加、人和机械设备超负荷工作等现象。为解决这一问题，港口通常采取集港高峰期收费、规定集卡到达时间段等方法。集卡预约系统是各国为解决这一问题而普遍采取的一种方法，通过预约系统码头可以提前做作业准备计划，合理分配堆场资源。集卡可以选择合适的时间送箱，避免出现某一时段集卡集中到达造成码头拥堵的现象，因此集卡预约系统可以提高码头的运营效率。但在实际集港过程中，因为一些不确定性因素预约系统有时并不能有效发挥其作用。如预约集卡在集港过程中会因为交通、天气或者人为等原因失约，不能在预约时段内准时到达。如果不对失约集卡进行处理，集卡预约系统将形同虚设。因此应及时对失约事件进行处理，减小失约事件对码头的影响。

现阶段集装箱码头出口箱堆存优化问题的研究按照作业阶段分类可以分为集港前的堆存优化和集港后的码头的装船作业效率优化两方面。其中集港前的堆存优化问题主要以优化堆存时出口箱落箱位的选择为主，码头的装船作业效率优化方面主要以减少装船作业时的预翻箱数为主。

在出口箱落箱位选择优化方面，Kim等[1]考虑了箱重因素，以最小化翻箱数为目标建立了实时决策最小生成树模型，并用动态规划算法进行求解；Lin等[2]以最小化场桥移动距离和作业时间为目标，建立了双目标规划模型，并设计了自适应启发式算法进行求解。Luo等[3]针对出口箱的箱位分配问题，考虑集卡作业与箱位分配的协调优化问题，以最小化船舶在港等待时间为优化目标建立了混合整数规划模型，并基于模型特点设计了遗传算法进行求解。Gharehgozli等[4]考虑船舶离港时间的不确定性，建立了以最小化翻箱数为目标的数学模型，并设计了模拟退火算法进行求解。Chang等[5]以平衡街区间作业量和翻箱数为优化目标，建立了两阶段调度模型，并设计了算法进行求解。Shen等[6]为了实现堆场的实时调度性，将机器学习方法应用到了某一个特定贝位内的出口箱堆存问题中，并在可接受时间范围内得到了优化方案。

李隋凯等[7]针对自动化码头中出口箱进场堆存作业问题，使用动态规划算法设计了一种多阶段动态规划算法。实验结果表明，该算法可使翻箱数在原基础上降低20%。黄子钊等[8]针对自动化码头中出口箱的箱位分配问题，以最小化街区不均衡程度和翻箱数为目标建立了多目标混合整数规划模型，并设计了基于强化学习的超启发式算法进行求解。周鹏飞等[9]提出了一种出口箱交箱次序与箱位分配的三维图表示法，并在此基础上构建了基于图的以最小化场桥作业成本和翻箱数为目标的优化模型，并设计了改进禁忌搜索算法；周鹏飞等[10]在进出口箱混合堆存下，以最小化压箱量和龙门吊移动距离及箱位偏移量为优化目标，建立了干扰恢复模型，并设计了局部加速的改进禁忌搜索算法。邵乾虔等[11]通过马尔可夫预测方法将不确定交箱次序转为一定概率保证下的确定交箱次序，建立了两阶段优化模型，并设计了静态和动态求解算法，通过仿真实验证明了模型和算法的有效性。范厚明等[12]在集卡预约机制下，为缓解高峰时段下集卡不规律到达所导致的拥堵问题，以降低码头堆场运营成本为原则，建立了以最小化调用集卡数量为目标的优化模型。马梦知等[13]针对送箱集卡随机到港引起的场桥作业不均衡问题，建立了以最小化总时间成本为目标的双层规划模型，并设计了遗传算法求解。邵乾虔等[14]构建了以时间残值矩阵为核心的线性仿真数学模型，并基于该模型提出了码头集疏港联动预约模式。

在提高码头的装船作业效率方面，Maldonado等[15]为了减少预翻箱数，以最小化船舶在港等待时间为优化目标建立了箱位分配模型，并设计了算法进行求解。Zheng等[16]研究了在进出口箱混合堆存的堆场中，街区内只有一台场桥时的作业问题。以场桥作业总延迟时间最小化为目标函数，建立了两阶段规划模型，并设计了基于一定规则的启发式算法进行求解。Zheng等[17]研究了在进出口箱混合堆存的堆场中，同一街区内有两台场桥同时作业的问题。在两台场桥作业时会发生干扰的前提下，建立了以场桥作业总延迟时间最小化为目标的数学模型，并设计了启发式算法进行求解。Galls等[18]以最小化堆场作业时间和提箱作业时间为目标，建立了混合整数规划模型，并提出了基于邻域搜索的启发式算法进行求解，在堆场作业和装船作业两个方面同时完成了优化和改进。Msakni等[19]以单个出口箱为作业单位，建立了码头岸桥作业调度优化模型，并设计了基于图搜索和割平面法的算法，并求得了问题的精确解。

郑红星等[20]在保持场桥间安全距离的强约束条件下，建立了以场桥行驶时间最小为优化目标的线性规划模型，并设计了分支定价法进行求解。孔靓[21]建立了平衡预翻箱和翻箱量的出口箱堆场多资源协同优化双层规划模型，上层模型以最小化装船时间为目标，建立了出口箱落箱位分配模型。下层模型根据上层模型生成的堆存方案生成预翻箱方案。郑红星等[22]以最小化内集卡等待时间为目标，建立了带有惩罚因子的混合整数规划模型，并设计了混合和声模拟退火算法，实现了实时预翻箱。

在现有的研究成果中，对上述中外文献综述梳理可以看出，针对出口箱堆场作业优化问题的研究主要集中于以下两个方面，分别是堆存阶段的箱位选择问题和装船阶段的提箱优化问题。对问题的切入点大致可以分为降低翻箱率、最小化场桥或者集卡移动距离、平衡街区设备之间的作业量等，存在的主要问题有多数研究直接将集装箱的到达信息作为确定的已知条件，或者根据预约信息来近似确定集装箱的到达顺序。然而实际作业中集装箱的到达顺序难以确定，存在着一定的不确定性，所以这些研究无法有效解决实际作业中出口箱的迟到、早到带来的扰动。针对集卡到达的不确定性，一些学者通过先建立确定性模型，再使用滚动调度的方法进行处理。如徐伟宣等[23]在滚动调度的基础上，研究了进出口箱混合堆存下箱位分配问题。但是由于滚动调度方法本身的周期性，使其在调度周期内的调度方案性能较差，从而影响调度效果。

因此现针对集卡到达存在一定不确定性的特点，以失约发生后对失约箱的响应与处理为切入点，建立以最小化翻箱数和场桥移动距离为优化目标的模型，并设计基于邻域搜索的实时调度启发式算法进行求解。力求帮助港口方在出现失约事件时，能够对失约箱做出实时调度，降低失约事件对码头作业的影响。

1 问题描述

为了提高港口的运营效率，港口通常采用集卡预约系统。预约系统下的出口箱集港的过程可以大致分为客户向港口申请预约交箱、港口方编制出口箱堆存方案以及出口箱入港堆存3个阶段。通过集卡预约信息可以获得集装箱的数量、箱型、尺寸、挂靠港口以及预约交箱次序等信息，港口根据这些信息编制初始堆存计划。实际交箱时，港口根据初始堆存计划，将出口箱放置到指定位置，并由场桥完成后续作业。

集装箱某街区内的初始堆存计划示意图如图1所示。根据预约信息，如果集卡能够准时交箱，那么该栈位内的堆存示意图如图1栈5中所示，括号外数字代表集装箱的交箱次序，括号内的数字代表集装箱的翻箱权重。翻箱权重由预约信息中的集装箱的重量和目的港确定，即由Fi=Zgi+zi确定。其中Fi为第i个出口箱的翻箱权重，gi为第i个出口箱的目的港，zi为第i个出口箱的质量。翻箱权重越大越早装船。此时该方案为最优方案，翻箱数为0，场桥没有额外的移动距离。如果集港过程中某个集装箱的交箱时间早于或者晚于其他的集装箱，如图1栈2中所示，则会造成翻箱。同时，场桥移动距离和集装箱的交箱次序是紧密相关的，随着交箱次序的变动，场桥可能产生额外的移动距离。

当失约事件发生时，如图2所示为箱4迟到，如果不对失约箱进行处理，直接将其放置在预约信息中对应位置，将会增加额外的场桥移动距离和翻箱数。而通过本文算法可以将其放置在合理的位置，如图3所示，从而减少失约事件对码头整体作业的影响。

图1 街区内堆存计划示意图Fig.1 Sketch map of the stacking plan in a block

图2 失约发生前堆存状态Fig.2 Stacking status before no-showing event occur

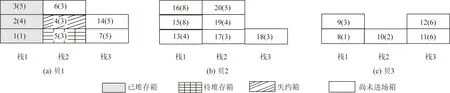
图3 对失约箱进行箱位再分配Fig.3 Slot relocation of the no-showing container

2 模型构建

2.1 前提假设

(1)出口箱均为20 in(1 in=30.48 cm)标准集装箱。

(2)待分配街区为指定某一个街区。

(3)根据集卡预约信息，集装箱的预约交箱时间、重量、目的港等信息已知，初始堆存方案根据预约信息已知。

(4)按照装船时长途箱和重箱优先装船的原则，以短途箱压长途箱、轻箱压重箱的方法计算翻箱权重。

(5)实际交箱时间与预约交箱的时间差值近似服从正态分布N(tk,σ),tk为出口箱k的预约交箱时间，不同取值的σ用来模拟生成不同失约等级的集卡实际到达信息。

2.2 符号说明

I={i|i=1,2,…,|I=E1+E2|}：出口集装箱的集合。

B={b|b=1,2,…,|B|}：街区内贝位的集合。

L={l|l=0,1,…,|L|}：贝位中栈的集合。

H={h|h=0,1,…,|H|}：栈内层数的集合。

Vb：贝位b的额定存放箱量。

α：调整系数。

β：调整系数。

E1：失约事件发生时，已进场的出口箱数。

E2：失约事件发生时，待进场的出口箱数。

Fi：第i个出口箱的翻箱权重。

gi：第i个出口箱的目的港编号。

A：一个充分大的正数。

Zi：第i个出口箱的质量，Z为最大质量等级。

Fi=Zgi+zi：翻箱权重计算公式。

yi：第i个出口箱所在的贝位。

Gb：失约事件发生时，贝位b中已堆存的出口箱量。

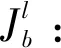
2.3 混合整数规划模型构建

式(1)为最小化场桥移动距离和翻箱量。

(1)

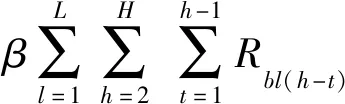
(2)

约束条件：

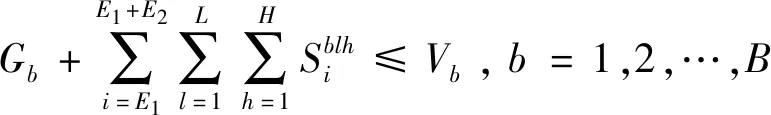
(3)

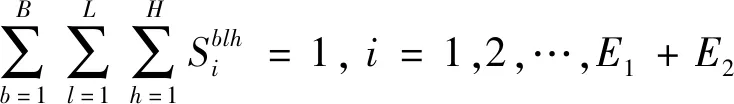
(4)

l=1,2,…,L

(5)

3,…,H(6)

(7)

ARbl(h-t)≥0

(8)

…,E1+E2

(9)

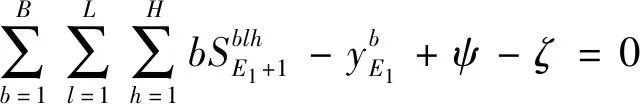
(10)

ωi≥0，ξi≥0，ψ≥0，ζ≥0，i=1,2,…,

E1+E2

(11)

2.4 模型验证

以盐田集装箱码头数据为基础，初始堆存方案利用集卡预约信息得出，不同失约等级的集卡到达信息由正态分布N(tk,σ)模拟生成，根据码头实际操作经验，α取0.4，β取0.6。算法的开发平台为MATLAB2019a，运行环境为CPU-AMD3900X 3.8 GHz，64 G。每组数据均为10次实验求得结果的平均值。

本模型可用CPLEX求解，分别取区段规模为1个贝位×3个栈×3层，2个贝位×3个栈×3层，1个贝位×5个栈×4层，2个贝位×4个栈×4层，3个贝位×4个栈×3层，25个贝位×6个栈×4层，6个不同规模进行对比。对比结果如表1所示。

针对小规模问题，CPLEX能够取得模型的最优解，证明了本文模型的有效性。但随着规模的增大，算法时间消耗程指数式增长。在CPLEX求解箱量规模为3×4×3时，算法耗时为6.2 h，不符合实际操作要求。本文算法与最优解比较接近，时间消耗也比CPLEX解决大规模问题要小，同时也能解决大规模问题，能够满足实际要求。

3 算法设计与数值实验

3.1 算法设计

针对现实规模问题，现有商业软件无法在有限时间内求得最优解。为此，提出了基于邻域搜索的启发式算法。预约信息已知，初始堆存方案根据预约信息得出，并将初始堆存方案作为启发式算法的初始解。每一个出口箱到达，就对其进行判断，如果其到达次序与预约信息相符，即按照初始堆存方案进行；如果不相符，即发生失约，则对失约箱进行箱位再分配。

集港过程中，假设共有i个出口箱预约交箱，每个出口箱交箱时刻视作一个决策节点，共做出i次决策。设S为预约交箱次序，Si为第i个到达的出口箱，P为出口箱实际到达次序，Pi为第i个实际到达的出口箱，Mi为第i个出口箱到达时当前堆场的状态，Ni为第i个出口箱到达前堆场的堆存方案。

表1 本文算法与CPLEX结果对比Table 1 Comparisons between this article’s algorithm and CPLEX

每当一个出口箱到达时，将P与S做一次对比，如果一致，则按当前堆存方案执行；如果不一致，即Pi≠Si且P(1,2,…,i-1)=S(1,2,…,i-1),则对该失约箱进行箱位再分配。箱位再分配时首先对失约箱产生其再分配集合Qi，Qi中包括失约箱与预约信息中失约箱所在贝位内尚未堆存集装箱的箱位交换集合以及失约箱与其他贝位中空箱位的交换集合。模型目标函数作为评估函数对Qi中的解进行评估，选择目标函数值最小的解为最优解，其对应的箱位为当前失约箱i的分配箱位。在状态Mi的基础上堆存失约出口箱i后生成Mi+1，并更新堆存方案为Ni+1。

基于邻域搜索的启发式算法的具体步骤如下。

步骤1通过预约信息生成的初始堆存方案作为初始解，i=0，Q0=φ，N0为初始堆存方案，M0为空堆场。

步骤2若i=I，则算法终止，输出最终堆存方案。否则i=i+1。

步骤3判断实际到达次序Pi和预约次序Si是否匹配，若匹配，则按照当前堆存计划Ni进行；若不匹配，转至步骤4。

步骤4根据当前堆存状态Mi及预约信息生成失约箱i的可分配区域Qi，模型目标函数作为评估函数对Qi中的解进行评估，选择目标函数值最小的解为最优解，若箱位不唯一则等概率选择其中一个，其对应的箱位为当前失约箱的分配箱位。

步骤5确定失约箱i的最优堆存箱位，更新堆存状态Mi+1和堆存方案Ni+1。转至步骤2。

设m、n均为出口箱编号，则设计该启发式算法中需要满足以下5个原则。

(1)针对失约箱i，将失约出口箱i及其在预约信息中所在贝位bi中未进场的出口箱加入到集合C，则箱位交换对为(m,n)。

(2)l为失约箱i在街区中可分配的含有空箱位的栈位，bi为出口箱i所在的贝位，l∈Vi=[max(0,bi-1),min(bi+1,B)]，使空栈位的选择在合理的范围内。

(3)搜索邻域集合包括箱位交换以及箱位和空箱位的交换，即Qi=(m,n)+(m,l)。

(4)可交换箱对(m,n)满足，|km-kn|+|Fm-Fn|≤15，km和kn分别为箱m、n的交箱次序，Fm和Fn分别是箱m、n的翻箱权重，避免箱位交换过程中产生较大的作业成本。

(5)若Qi中包含(m1,n1)(m2,n2)，则m1≠m2≠n1≠n2，除去不满足条件的不可行解。算法流程图如图4所示。

3.2 算法对比

3.2.1 策略1：按原计划进行

即虽然出现失约事件，仍然按照原堆存方案执行。

3.2.2 策略2：传统作业算法

即基于贪婪算法思想的启发式算法。

步骤1通过预约信息生成的初始堆存方案作为初始解，i=0，Q0=φ，N0为初始堆存方案，M0为空堆场。

步骤2若i=I，则算法终止，输出最终堆存方案。否则i=i+1。

步骤3判断实际到达次序Pi和预约次序Si是否匹配，若匹配，则按照当前堆存计划Ni进行；若不匹配，转至步骤4。

步骤4判断场桥当前所在贝位内是否有空箱位，若存在则将所有可交换对加入到Qi中，模型目标函数作为评估函数对Qi中的解进行评估，选择目标函数值最小的解为最优解，若箱位不唯一则等概率选择其中一个，其对应的箱位为当前失约箱的分配箱位。若场桥当前所在贝位内无空箱位，则依次选择判断相邻贝位内是否有空箱位，直到找到一个空箱位。

步骤5确定失约箱i的最优堆存箱位，更新堆存状态Mi+1和堆存方案Ni+1。转至步骤2。

策略2相比于本文算法并没有充分利用预约信息，不能从全局出发，而是基于贪婪算法思想，通过就近原则达到局部最优。

3.3 大规模算例实验

如表2所示给出了在失约等级3下，本文算法与策略1、策略2的结果对比。可以看出本文算法和策略2均明显优于策略1。针对小规模问题，本文算法和策略2差异不大。但随着箱量规模的增大，当箱量规模在5×6×6以上时，本文算法在翻箱数上开始明显优于策略2，且规模越大优势越明显。而场桥移动距离劣于后者，是因为策略2总体遵循就近堆存原则。二者算法耗时均符合实际操作要求。

在箱量规模为18×6×6，失约等级为3下，本文算法迭代图如图5所示，横坐标为迭代次数，纵坐标为模型目标函数值。算法呈阶梯状收敛，算法消耗时间为12.3 s，在循环186次后达到收敛，说明本文算法可以较短时间内实现实时调度，并且收敛值相较于初始值有明显改善。

3.3.1 情景1：同一失约等级时，对比不同箱量规模下两种算法算例结果

如图6所示为在失约等级3时，不同箱量下两种算法模型目标函数值对比图。可以看出，小规模算例下两者总成本差距不大，随着算例规模的增大，本文算法开始明显优于策略2。其原因在于小规模箱量下，无法充分发挥本文算法基于预约信息对失约事件的实时调度性。随着箱量规模的增大，本文算法的全局最优性相较于策略2的局部最优性开始凸显优势，并且随着箱量规模的增大，优势会越来越大。

图4 基于邻域搜索的启发式算法流程图Fig.4 Flow chart of heuristic algorithm based on neighborhood search

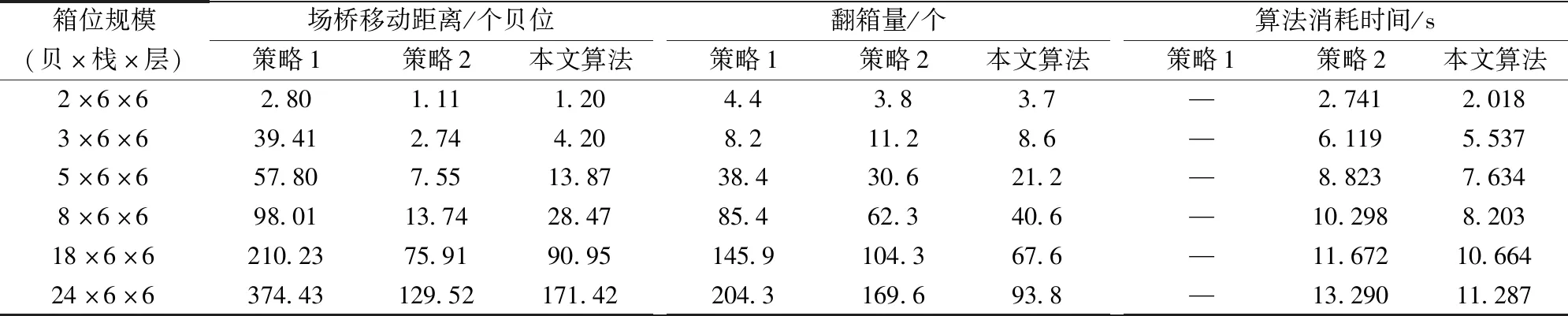
表2 本文算法与两种传统策略结果对比Table 2 Comparisons between proposed algorithm and two traditional strategy

3.3.2 情景2：同一失约等级时，对比不同箱量规模下两种算法场桥移动距离和翻箱数

如图7所示为在失约等级3时，不同箱量规模下两种算法场桥移动距离和翻箱数对比图。当箱量规模较小时，本文算法和策略2在场桥移动距离和翻箱数上的差距很小。随着箱量规模的增大，两种算法在场桥移动距离和翻箱数上都有所增加，本文算法在场桥移动距离上增加较快，策略2在翻箱数上增加较快。基于就近堆存原则的策略2在场桥移动距离上一直优于本文算法，但在翻箱数上一直逊于本文算法，鉴于实际作业中翻箱作业成本高于场桥移动成本，实验结果可以接受。

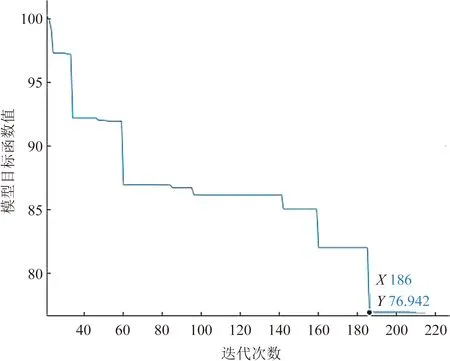
图5 启发式算法收敛图Fig.5 Convergence graph of heuristic algorithm

3.3.3 情景3：同一箱量规模时，对比不同失约等级下两种算法场桥移动距离和翻箱数

如图8所示，在箱量为18×6×6的箱量规模下，随着失约等级的增大，失约到达的出口箱越来越多，策略2不能针对失约出口箱进行有效处理，所以与本文算法在翻箱数上的差距越来越明显。在失约等级6时，本文算法相较于策略2在翻箱数上有33.3%的优化率，具有较高的实用性。由于策略2遵循就近堆存原则，所以场桥移动距离在各个失约等级上一直优于本文算法，但是在有效降低翻箱数的前提下，总目标函数值本文算法结果一直优于策略2，即实验结果可以接受。

3.3.4 情景4：同一箱量规模时，对比不同失约等级下两种算法算例结果

如图9所示为取算例为18×6×6的箱量规模，不同失约等级下，两种算法目标函数值对比。可以看出随着规模的增大，本文算法相对于策略2的改进效果越来越明显，在失约等级1时，本文算法相对于策略2仅有7.5%的改进率。而在失约等级6时，有20.91%的改进率。这是因为当σ较小时，出口箱的实际到达序列和预约信息差异较小，所以本文算法优势不明显。随着σ的增大，实际交箱时间和预约交箱时间有较大差异时，本文算法能够对失约出口箱合理分配其落箱位，降低翻箱数和场桥移动距离，从而降低失约事件对码头作业系统整体的扰动。

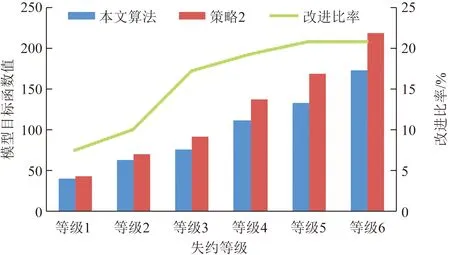
图8 同一箱量规模、不同失约等级下，两种算法场桥移动距离和翻箱数对比Fig.8 Contrast graph of the number of reshuffles and gantry-crane traveling distance for two algorithm under the same container scale and different no-showing level

图9 同一箱量规模、不同失约等级下，两种算法算例结果对比Fig.9 Contrast graph for two algorithm under the same container scale and different no-showing level

3.3.5 情景5：不同情形下，本文算法相较于传统算法策略2算例实验结果改进分布图

本文算法和传统算法策略2的算例实验结果的改进分布图如图10～图12所示。在失约等级3，箱量规模为18×6×6时，本文算法得到的所有算例结果中，较优解占比为90%，最大改进程度为36.62%，平均改进程度为17.22%。而在箱量规模为5×6×6时，最大改进程度和平均改进程度分别是47.21%和14.68%，较优解所占比重为86%。数据显示，相同失约等级下，随着箱量规模的增大，算法的改进效果越明显，较优算例所占比重也越大。在箱量规模为18×6×6下，在失约等级6时，较优解所占比重为97%，最大改进程度和平均改进程度分别为44.45%和21.21%。综上可知，随着失约等级和箱量规模的增加，本文算法相较于传统算法策略2的改进程度越来越大。

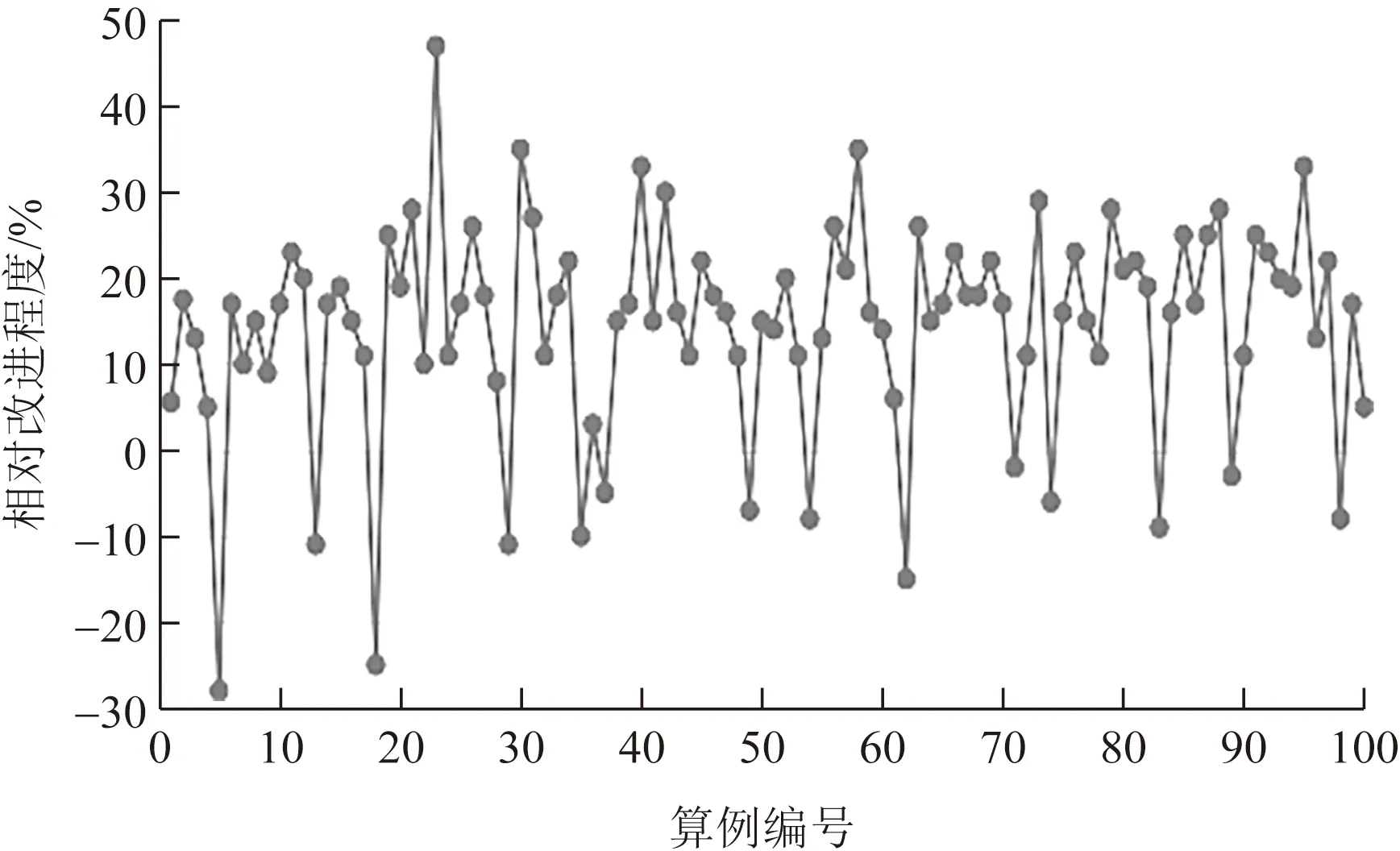
图10 箱量规模为5×6×6、失约等级为3时，算法相对改进程度分布图Fig.10 Relative improvement ratio graph of two algorithm when container scale is 5×6×6 and no-showing level is 3

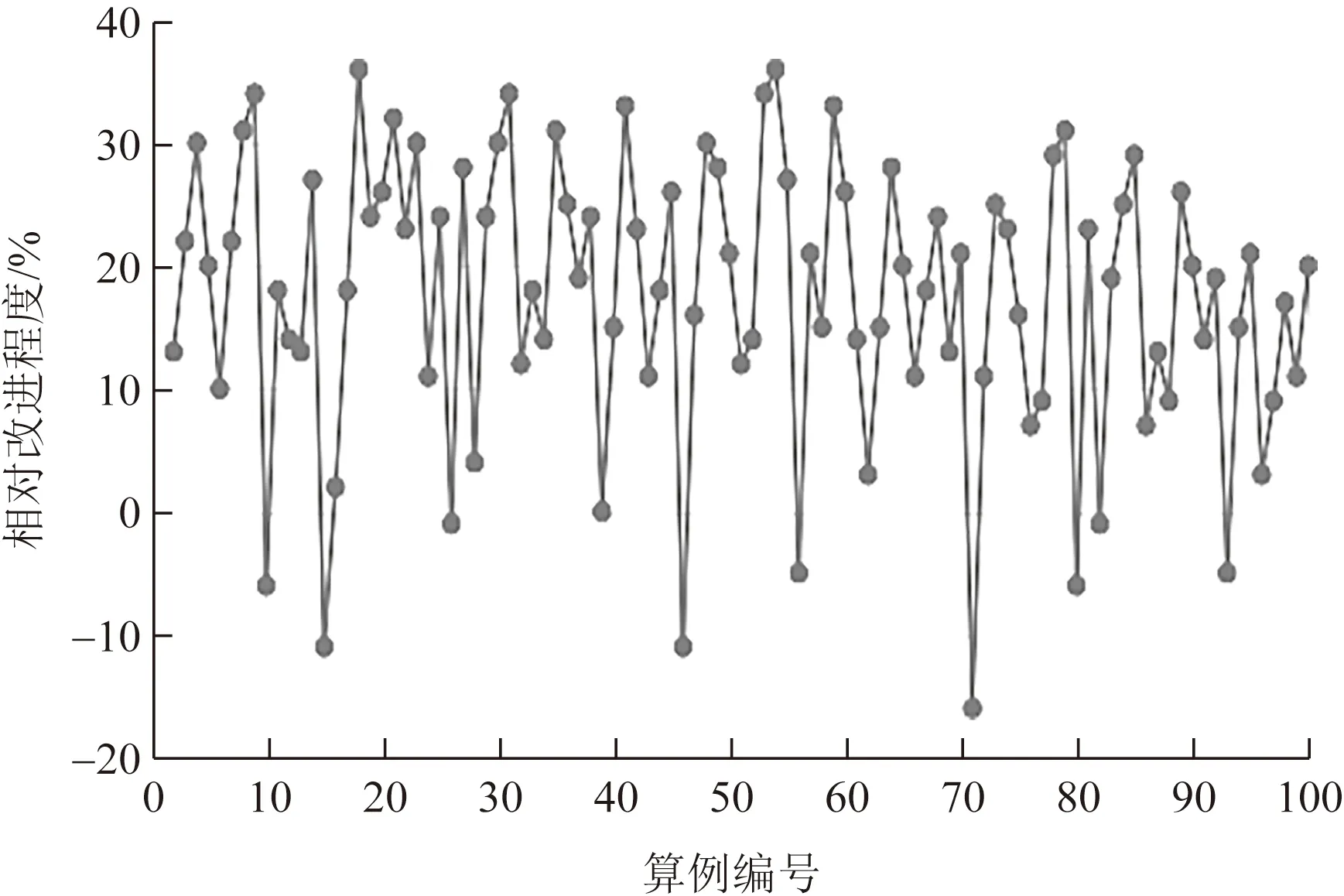
图11 箱量规模为18×6×6、失约等级为3时，算法相对改进程度分布图Fig.11 Relative improvement ratio graph of two algorithm when container scale is 18×6×6 and no-showing level is 3

图12 箱量规模为18×6×6、失约等级为6时，算法相对改进程度分布图Fig.12 Relative improvement ratio graph of two algorithm when container scale is 18×6×6 and no-showing level is 6

4 结论与展望

集卡预约系统可以有效缓解码头拥堵问题，提高码头作业效率。但集卡常常因为各种现实原因不能准时到达而导致失约事件的发生。对于港口方而言，虽然集卡预约系统可以大幅降低码头拥堵出现的情况，但是在失约事件发生时，针对失约出口箱一定要设计出可以实时选择失约出口箱落箱位的调度机制。这样才能完成对失约事件的快速响应处理，降低失约事件的发生对整个码头系统的扰动，进而提高码头的作业效率。

通过对失约出口箱的落箱位再分配，研究了不同箱量规模、不同失约等级下的集卡到达对码头作业的影响。建立了以最小化场桥移动距离和翻箱数为目标的数学模型，设计了基于邻域搜索的启发式算法，并通过设计规则优化了算法的搜索方向和空间，使其计算时间在可接受范围内并能得出满意解。算例实验中展示了不同箱量规模、不同失约等级下，场桥移动距离和翻箱数以及模型目标函数值的对比，并得出了以下结论。

(1)集装箱的交箱次序对街区内的场桥移动距离和翻箱数的影响较大，在集卡预约系统下，随着失约等级的升高，算例实验表明相较于准时到达或者低失约等级下，高失约等级下的翻箱数和场桥移动距离都有较大的升高幅度。在箱量规模为18×6×6下，失约等级6相较于失约等级1在场桥移动距离和翻箱数上分别有213%和440%的提高，说明了集装箱的交箱次序对出口箱的堆存有显著影响。

(2)实验结果表明本文算法相较于传统算法有较大改进，且改进程度随着箱量规模、失约等级的提高而提高，在算例为18×6×6箱量规模时，不同失约等级下，模型目标函数值平均有15.70%的改进率，最大有20.91%的改进率。在失约等级3时，不同规模箱量下平均有11.12%的改进率，最大有19.2%的改进率。在不同情形下，本文算法相较于传统算法策略2算例实验结果改进分布图也验证了本文模型及算法的有效性，为进一步的研究打下了基础。

后续研究拟从以下3个方面展开。一是考虑进口箱或者进出口箱混合堆存下箱位分配问题；二是尝试结合装船信息，将岸桥及内集卡等其他资源联系起来协同优化；三是尝试结合预约信息与历史实际到达信息，得到一定概率统计下的模拟到达信息，进而提高算例的真实性。