基于改进鲸鱼算法的半主动悬架PID 控制

张素君,杨文强

（河南科技学院机电学院,河南新乡 453003）

汽车悬架的控制效果影响车辆舒适性和安全性.半主动悬架使用无源可控元件调节悬架的阻尼或刚度,成本较低却有较好的控制效果[1].因此,半主动悬架的控制方法及效果研究引起了诸多学者的重视.

PID 控制因其原理简单、鲁棒性[2]和实用性强,广泛应用于各种工业控制系统,但PID 控制器的控制效果依赖于参数的整定,传统参数整定方法依赖经验,且对控制对象适应性差,影响控制器设计效率.因此,智能优化算法如粒子群算法[3-5]、遗传算法[6]和ILMI 算法[7]等应用于PID 控制器参数整定,改善了PID控制器的控制效果,开辟了一条不依赖经验整定合理控制参数的方法.鲸鱼优化算法(The whale optimization algorithm,WOA)[8]是较为新颖的一种智能优化算法,由于算法原理简单、参数少、优化性能强等优点,广泛用于各个领域,如神经网络、特征提取、图像分割和生产调度以及电力系统控制的PID 参数调节等优化问题[9-14].本文提出改进的鲸鱼优化算法(improved whale optimization algorithm,IWOA)对PID 控制器进行参数整定,并应用于汽车半主动悬架控制,通过仿真验证控制效果.

1 悬架模型

汽车的整体机械结构十分复杂,如果建立整车模型,其研究分析会变得繁琐复杂,不利于研究[15].综合考虑,利用汽车结构的对称性,建立车辆二自由度1/4 半主动悬架模型,如图1 所示.

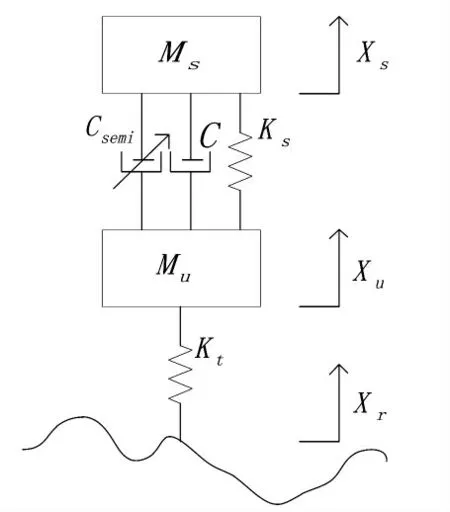
图1 二自由度1/4 半主动悬架模型Fig.1 Two-degree-of-freedom 1/4 semi-active suspension model

根据图1,建立系统动力学方程

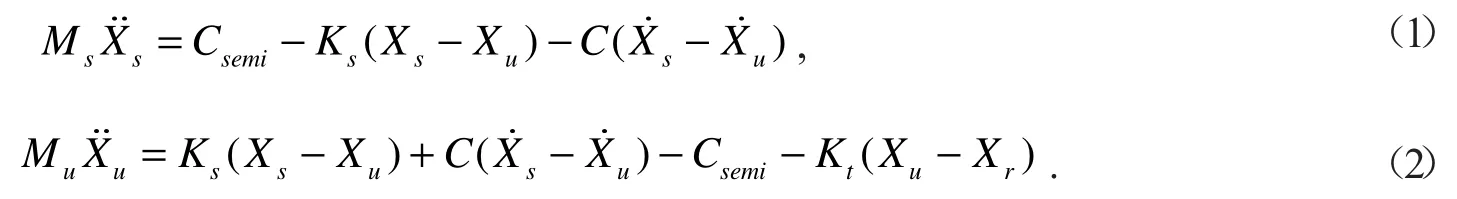
模型参数如表1 所示.

表1 悬架模型参数Tab.1 Suspension model parameters

通过对模型分析,选取状态变量,X=[X1X2X3X4]T,其中X1=Xs−Xu,X2=X4=

选择系统输出变量Y=[y1y2y3y4]T,其中,分别表示车身垂直加速度、悬架动扰度、轮胎动载荷、非簧载质量加速度.

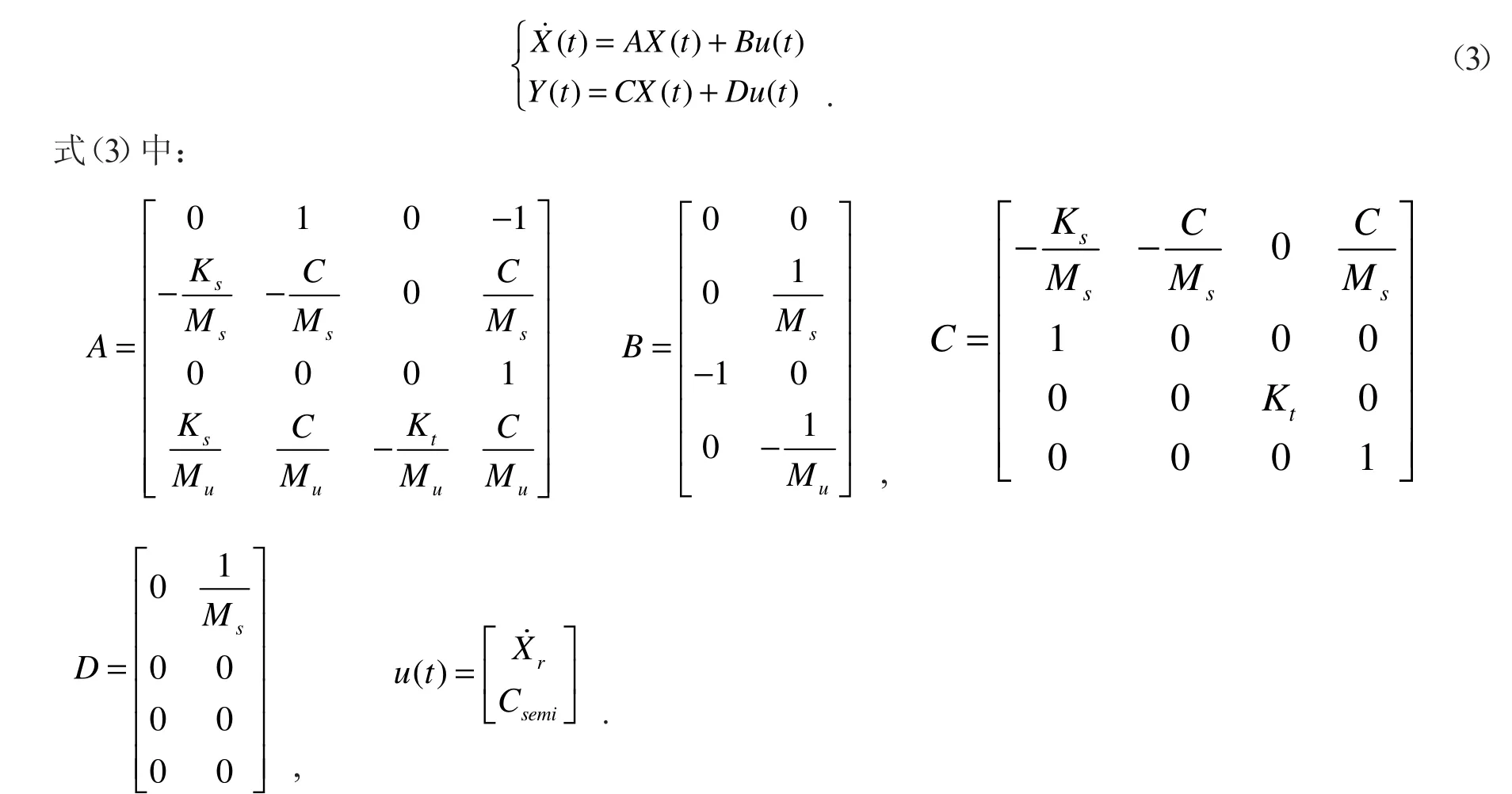
由式(1)和式(2)得状态空间表达式

2 半主动悬架PID 控制

PID 控制是一种经典的控制方式,系统由设定值与系统实际输出值的差作为偏差,并对其进行比例、积分、微分运算求得控制量,控制被控对象.

半主动悬架PID 控制系统结构图如图2 所示.

图2 半主动悬架PID 控制系统结构图Fig.2 Structure diagram of PID control system of semi-active suspension

PID 控制器控制规律为

式（4）中:KP为比例调节系数;KI为积分调节系数;KD微分调节系数;e(t)为偏差,是设定值r(t)与实际输出值y(t)之差,即e(t)=r(t)-y(t);u(t)为被控对象的输入.

3 改进的鲸鱼优化算法

鲸鱼优化算法[8]是Mirjalili 在2016 年提出的一种新颖的智能优化算法,受到座头鲸捕食行为的启发,发现猎物后,座头鲸以螺旋上升方式游到猎物附近并包围它,同时吐出泡泡形成泡泡网攻击猎物,算法中有三种捕食猎物方法,即围捕、泡泡网攻击和随机搜索.这些行为的数学描述,构成了算法的主体,描述如下:

(1)围捕猎物.由于猎物位置未知,算法中采用当前最优个体位置作为猎物位置,其余个体将更新自己的位置向其靠近,该行为通过下面数学表达式描述

式(5)中:t 为当前代数,X(t)和X*(t)分别表示为第t 代个体和到第t 代为止的最优个体;A 和C 分别指系数向量,D 表示个体X(t)和X*(t)之间的距离,||表示绝对值,表示向量点乘,另外,r 为[0,1]随机向量,而a为从2 到0 线性减少的量,由式(6)表示

(2)泡泡网攻击猎物.螺旋上升伴随泡泡网攻击,数学描述如下

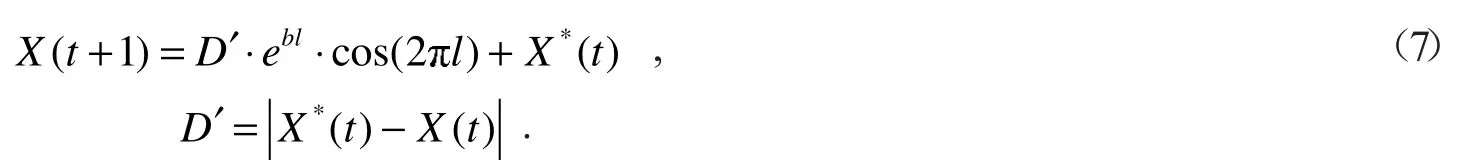
式(7)中:D'表示向量X(t)和X*(t)之间的距离,d 是一个表示螺旋形状的常数,l是一个随机数,l∈[−1,1].

由于鲸鱼围捕猎物和泡泡网攻击是同时进行的,为了建模这种同时的行为,围捕猎物和螺旋模型更新位置各以50%的概率被选择更新个体位置,即

(3)随机搜索猎物.实际上座头鲸在围捕、攻击猎物的同时还会随机搜索猎物,其模型为

式(9)中:Xrand(t)为种群中随机选择的个体,D 为随机个体Xrand(t)和个体X（t)的距离,由式(10)表示

鲸鱼优化算法的优化性能严重依赖全局搜索和局部搜索的平衡,式(6)中的a 随着搜索的过程,从2线性减少到0,可以平衡算法的全局调节搜索能力和局部搜索能力,即当进行随机搜索,全局搜索能力强,而当,则利用最优个体进行局部搜索,寻找最优个体.也就是说,a 是线性变化的,即进化的前半段进行全局搜索,后半段进行局部搜索.因此,a 的变化过程对算法的优化效果影响重大,但无论怎么选择要满足三个条件:①t=1 时,a=2;②t=Tmax时,a=0;③函数是减函数.

基于上面分析,本文提出基于反正弦函数a 的表达式,以求达到较好的优化效果.表达式如式(11)所示,不同a 表达方法的曲线图如图3 所示.

从图3 中可以看出,式(11)中表示的a(非线性arcsin)和式(9)中表示的(线性)相比,在迭代的初期a 变化较快后期变化较慢,应用到鲸鱼优化算法中,以进化500 代为例,可以使算法在迭代初期具有较强的全局搜索能力,在大约150～200 代完成全局搜索,有效的避免了算法过早陷入局部最优,后面有足够的代数进行局部搜索,可以找到较好的解,提高算法的优化性能,因此用式(11)表示a 的算法即为改进的鲸鱼优化算法,并用于优化PID 参数.

图3 a 由arcsin 和LCS 表示的收敛曲线比较图Fig.3 Convergence curve comparison chart a represented by arcsin and LCS

4 优化PID 控制

将改进的鲸鱼算法与PID 控制理论相结合,利用IWOA 整定PID 控制器参数.改进鲸鱼算法PID 控制系统(IWOA-PID 控制系统)结构图如图4 所示.

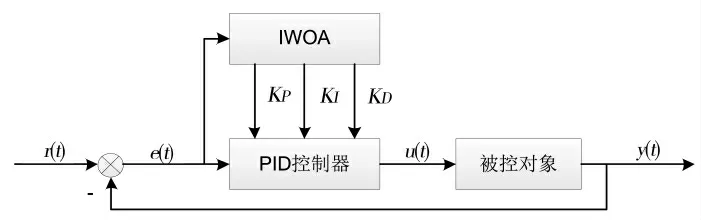
图4 IWOA-PID 控制系统结构图Fig.4 IWOA-PID control system structure diagram

首先根据被控对象数学模型建立目标函数,并根据目标函数计算适应度值;适应度值越大,说明选择该组参数(KP、KI和KD)PID 控制器的控制效果越好;本文以车身垂直加速度、悬架动扰度及轮胎动载荷作为性能评价指标[16],评价汽车的舒适度.适应度值是综合评价指标,用来评价PID 控制器的控制效果,由各个性能评价指标的均方根求出.根据多组仿真实验对比,悬架动扰度对控制效果影响很大,但对汽车舒适性的提升作用很小;车身垂直加速度对汽车乘坐舒适性的影响较大,作为主要的优化目标;轮胎动载荷影响着车辆行驶的安全性,是不可忽视的重要性能评价指标.因此,根据三个性能指标对舒适度的影响程度设置不同权值,设定车身垂直加速度权重为0.45,悬架动扰度权重为0.1,轮胎动载荷权重为0.45.本文设计适应度值L 计算公式为

式(12)中：Aps,Dps和Fps分别指被动悬架的车身垂直加速度、悬架动扰度和轮胎动载荷;而Asvs,Dsvs和Fsvs分别指半主动悬架车身垂直加速度、悬架动扰度和轮胎动载荷;sqr为求均方根值.

改进的鲸鱼优化算法(IWOA)整定PID 参数的流程图如图5 所示.

图5 IWOA-PID 控制系统流程图Fig.5 Flowchart of IWOA-PID control system

首先初始化种群,规模为NP,种群中的个体为D 维(D=3)(KP、KI和KD)向量,求出适应度值,应用改进的鲸鱼算法优化个体,并记录本代的最优个体和最优适应度值,导入控制器,如此循环,直到满足终止条件,输出最优个体及其对应的适应度值.

5 仿真与分析

5.1 仿真系统建立

选择路面输入为B 级路面且路面不平度系数Gq(n0)=64 ×106m2/,设置汽车时速为60 km/h.

在Matlab/Simulink 中构建汽车半主动悬架PID 控制系统仿真模型,如图6 所示.

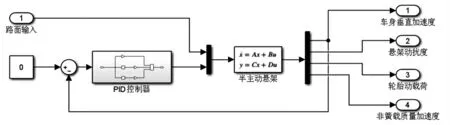
图6 半主动悬架PID 控制系统仿真模型Fig.6 Simulation model of PID control system of semi-active suspension

5.2 仿真结果分析

经验法与鲸鱼优化算法整定后的PID 控制器参数,如表2 所示.

表2 PID 控制器参数Tab.2 PID controller parameters

将两组参数值代入到PID 控制器中进行仿真,结果如图7、图8、图9 所示.

图7 车身垂直加速度控制效果对比波形图Fig.7 Comparison waveform chart of vehicle vertical acceleration control effect

图8 悬架动扰度控制效果对比波形图Fig.8 Comparison waveform diagram of suspension disturbance control effec

图9 轮胎动载荷控制效果对比波形图Fig.9 Comparison waveform diagram of tire dynamic load control effect

根据图(7)～(9)可以看出,经过WOA 算法优化的PID 控制半主动悬架的车身垂直加速度振幅较小,提升了车辆乘坐舒适性;轮胎动载荷振幅变化不明显,从波形图上难以分辨优化效果;对于悬架动扰度,波形振幅略有增加.由汽车悬架模型分析可知,车辆各性能评价指标之间是相互制约、相互影响的.将改进的差分进化算法每代优化出的参数代入PID 控制器中,并把各组参数(各个个体)控制下的性能评价指标绘制成散点图,如图10 所示.

图10 相关性对比散点图Fig.10 Correlation contrast scatter plot

由图10 可以看出,车身垂直加速度和悬架动扰度二者的均方根成负相关.由图8 可以看出,虽然PID 控制作用下汽车悬架动扰度增加,但其幅值在[-0.015,0.015]范围内.由表1 可知,汽车悬架动行程,限位为0.09 m,悬架在系统中的运动位移没有超过设计参数要求,因此PID 控制在改善汽车乘坐舒适性的同时不会对汽车结构造成破坏.

利用IWOA 算法整定后的PID 控制器参数,如表3 所示.

表3 IWOA-PID 控制器参数Tab.3 IWOA-PID controller parameters

将该组参数值代入PID 控制器中进行仿真,并与WOA-PID 控制器仿真效果进行对比,结果如图11、图12、图13 所示.

图11 车身垂直加速度控制效果对比波形图Fig.11 Comparison waveform chart of vehicle vertical acceleration control effect

图12 悬架动扰度控制效果对比波形图Fig.12 Comparison waveform diagram of suspension disturbance control effect

图13 轮胎动载荷控制效果对比波形图Fig.13 Comparison waveform diagram of tire dynamic load control effect

根据波形图可以看出,IWOA-PID 控制的半主动悬架的车身垂直加速度振幅进一步减小,且轮胎动载荷明显减小;IWOA 算法改善了悬架动扰度的控制效果,在提高车辆乘坐舒适性的同时保证了车辆结构的安全性.

5.3 仿真结果定量分析

计算WOA-PID 控制半主动悬架与IWOA-PID 控制半主动悬架系统中车身垂直加速度、悬架动扰度和轮胎动载荷的均方根值,如表4 所示.

表4 悬架控制系统性能评价指标对比Tab.4 Comparison of performance evaluation indexes of suspension control system

由表4 中数据对比分析可知,在车身垂直加速度、悬架动扰度与轮胎动载荷方面,IWOA-PID 控制器控制效果比WOA-PID 控制器控制效果更好.车身垂直加速度减小,性能改善了6.35%,提升了汽车驾驶的舒适性,减小了乘车时的“颠簸感”.轮胎动载荷减小了10.29%,进一步提升了汽车行驶的安全性,保证了汽车在行驶的过程中轮胎与地面的附着,提高操作稳定性.在悬架动扰度方面,IWOA 算法改善了WOA-PID 控制半主动悬架控制系统中悬架动扰度的控制效果,对汽车驾驶舒适性优化的同时保证汽车结构的安全性.

6 结论

本文建立了二自由度1/4 半主动悬架模型,应用PID 控制理论控制悬架运动,利用改进的鲸鱼优化算法整定PID 控制器参数,优化PID 控制器的控制效果,在Matlab/Simulink 中进行仿真实验,对比分析用IWOA 算法优化PID 参数的PID 控制器控制效果,并定量分析IWOA-PID 控制对系统性能的改善程度.仿真结果表明,采用IWOA-PID 控制,可以使车身垂直加速度和轮胎动载荷更小,提高汽车乘坐的舒适性和安全性.因此,改进的鲸鱼优化算法不仅提升了控制系统的设计效率,而且提高了控制系统的控制性能.