基于扰动观测器的微网逆变器鲁棒H∞控制策略
何国锋
(河南城建学院 电气与控制工程学院,河南 平顶山 467036)
0 引言
微电网是由新能源构成的小型电网,既可以与大电网相连接在并网模式下工作,也能够运行在孤岛模式下,为本地负载提供电能。逆变器作为连接微电网与新能源发电的重要接口设备,在孤岛模式下,能将可再生能源发出的电能经过转换供给本地负载。孤岛模式下的微网逆变器,在实际运行过程中会受到负载突变、滤波器元器件老化、直流侧电压波动等各种各样的扰动,影响微网逆变器的输出电能质量。逆变器作为新能源并网的关键部分,其控制器的设计直接影响微电网 系 统 的 电 能 质 量[1],[2]。
为了抑制系统扰动对孤岛微网逆变器的影响,增强微网系统的稳定性,提高微网逆变器的输出电能质量,国内外学者针对孤岛微网逆变器的电压控制方法及其系统的稳定性和稳态性能不断地开展研究。文献[3],[4]采用下垂控制的方法对孤岛微电网进行有功-频率、无功-电压的控制。孤岛微电网分布式电源具有的间歇性和波动性将会导致系统参数的摄动,而下垂控制器的动态性能有限,不具备抵抗系统大范围扰动的能力,因此容易造成系统输出电能质量下降,甚至造成系统不稳定的问题。文献[5]根据微网控制的多个性能指标,分别设计出具有动态虚拟阻抗的电压环和电流环。功率环的设计引入了自适应控制方法,采用自适应控制策略调整下垂系数,实现对微电网的控制。虽然多环控制能够弥补传统下垂动态性能不足的缺陷,但是控制器的设计过程复杂,计算量大,传感器数量过多,缺乏对于实际应用的考虑。文献[6]从微网系统电压精准控制的角度出发,基于内模原理设计出应用于微网逆变器的比例谐振电压控制器,以适应多种类型的负载。然而,单一谐振控制器只对固定阶次谐波有效,在实现总谐波含量较低时则需要多重控制器,而且谐振控制器对于频率过于敏感,易受系统扰动的影响。文献[7],[8]从系统扰动抑制的角度出发,基于状态反馈思想和LMI求解方法,设计出微网逆变器的鲁棒控制器,实现了对负荷扰动的抑制;但是,系统的动态性能不够理想,而且状态反馈过程中用到的传感器数量较多,不利于在实际系统中应用。文献[9]将线性自抗扰控制技术引入到微电网的控制器设计中,将输出电压误差的微分项引入到扩张状态观测器中,以提高观测精度,并在总扰动作用通道增加了一阶惯性环节,避免因扩张状态观测器带宽增加而引入噪声。由于系统待调参数较多,自抗扰控制器跟踪交流信号的速度有限,使系统的动态性能受限。
以上所述文献虽然针对微电网稳定性控制、扰动抑制和电压精确控制等进行了探讨,但是没有同时对微电网系统中存在的多参数摄动问题和负载切换问题加以深入地研究。本研究结合实际孤岛微网逆变器运行过程中存在的多参数摄动问题,基于鲁棒H∞控制理论,建立了逆变器的多参数摄动模型。本文根据多参数摄动边界和系统稳态性能要求设计了合适的权重函数;采用混合灵敏度设计方法求解逆变器的鲁棒H∞控制器;采用扰动观测器对负载投切时产生的电流扰动进行观测和补偿,以减小负载投切时对输出电压造成的影响。
1 多参数摄动的微网逆变器模型
孤岛微电网原理如图1所示。图1中最左侧为光伏发电、风力发电等可再生能源发电系统及其起到直流电压变换作用的DC/DC模块。储能系统为微电网不间断供电提供保障。逆变器作为微网系统与分布式电源连接的关键接口,起到电能变换的作用。
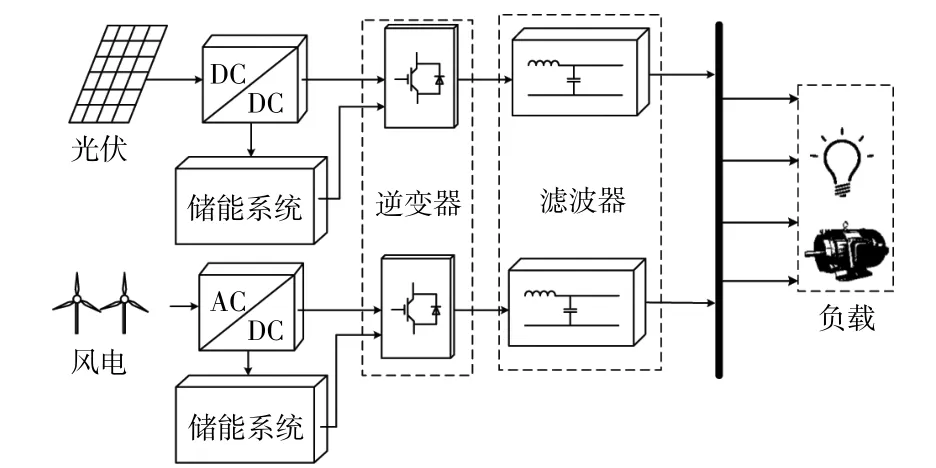
图1 孤岛微电网原理图Fig.1 Schematic diagram of islanding microgrid
本文以孤岛模式下的单相全桥逆变器作为研究对象,图2为其电路原理图。
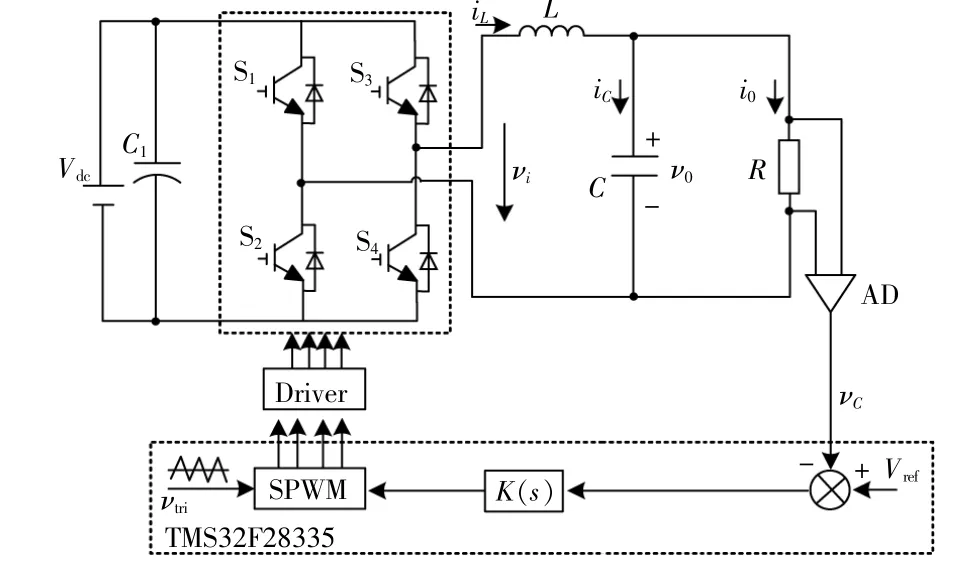
图2 孤岛微网逆变器电路原理图Fig.2 Schematic diagram of inverter under islanding mode
图2中:逆变器采用LC型滤波器;L为滤波电感值;C为滤波电容值;R为电阻性负载的阻值。电压环采用鲁棒控制策略和正弦脉宽调制方式,vtri为三角载波,其数字控制算法在DSP中实现。下面主要讨论逆变器在多参数摄动情况下电压控制环的鲁棒控制器设计方法。
假设载波信号频率远远高于正弦调制信号的频率,根据基尔霍夫电压和电流定律可以得出孤岛微网逆变器的连续时域模型[9],[10]:
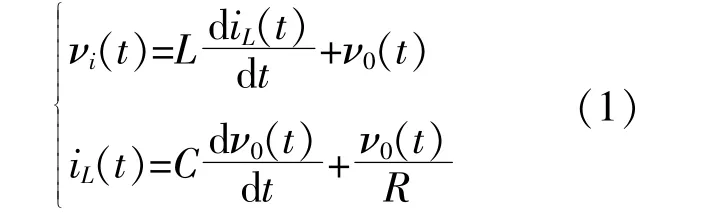
式 中:vi(t)为 逆 变 器 桥 臂 中 点 之 间 电 压;iL(t)为 流过 电 感 的 电 流;v0(t)为 滤 波 电 容 上 的 电 压;ic(t),io(t)分别为滤波电容和负载上的电流。
选 择 电 感 电 流iL(t)和 电 容 电 压v0(t)作 为 状态 变 量,令x=[v0(t)iL(t)]T,u(t)=vi(t),可 得 如 下状态方程:
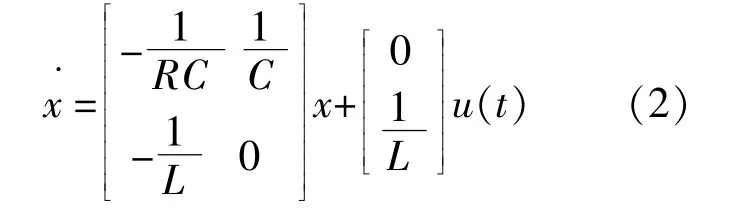
设微网逆变器系统中滤波器参数的基准值分别 为L0和C0,负 载 电 阻 的 基 准 值 为R0,令Gn(s)为微网逆变器系统中被控对象的基准传递函数:

在微网逆变器实际运行过程中,随着运行工况、负载功率变化,器件的参数会随之发生变化。假设滤波电感、滤波电容和负载参数摄动后的值分别为Lp,Cp,Rp,则考虑参数摄动后被控对象的传递函数可以表达为

基于单相逆变器的基准模型,本文采用乘性摄动的形式来表示被控对象的实际模型:G(s)=G0(s)[1+Δ(s)],其 中,Δ(s)为 乘 性 不 确 定 部 分。
图3为采用乘性摄动形式的系统模型。
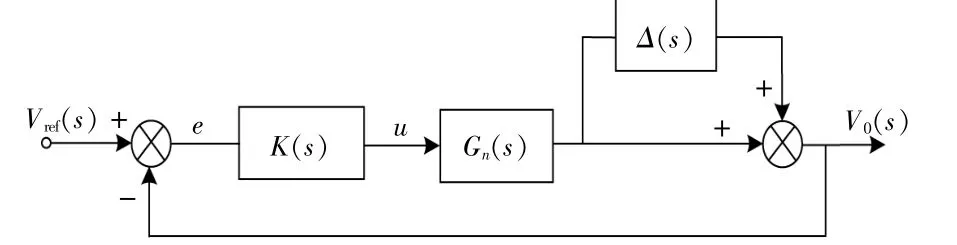
图3 采用乘性摄动形式的系统模型Fig.3 System model with multiplicative perturbation
如图3所示,经过代数变换可以得到乘性不确 定 性 Δ(s)如 下[11],[12]:
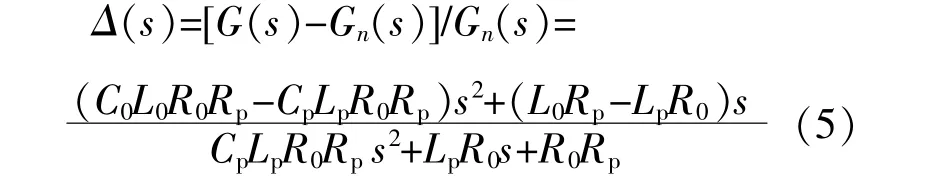
由式(5)可知,当器件参数实际值与基准值相等,即Lp=L0,Cp=C0,Rp=R0时,系 统 的 参 数 摄 动 量Δ(s)为零。考虑参数摄动有界,采用鲁棒控制策略预先设定参数的变化范围,参数在预定的范围内变化时,系统仍然能够稳定工作,并保持一定的鲁棒性能。本文所设定的逆变器基准参数和参数摄 动 范 围 如 下:R0=30Ω;L0=0.66 mH;C0∈22μF;Rp∈[20,40]Ω;Lp∈[0.3,0.9]mH;Cp=[10,30]μF。
2 鲁棒H∞控制器设计
鲁棒H∞控制在系统稳定、扰动抑制等方面得到广泛应用。当被控对象的数学模型中存在扰动时,所设计出的鲁棒控制器不仅可以维持系统稳定,而且能够保证设计所要求的鲁棒性能,在一定程度上弥补了现代控制理论的不足[13],[14]。
2.1 混合灵敏度分析
混合灵敏度优化理论可以同时解决系统的鲁棒稳定性和鲁棒性能,即多目标优化问题。本文采用混合灵敏度优化法设计微网逆变器的鲁棒控制器,以满足设计所需的静态特性和鲁棒稳定性。图4为混合灵敏度控制框图[15]~[18]。图4中:w为参考输入信号;e为误差信号;u为控制器产生的控制信 号;v0为 微 网 逆 变 器 的 输 出 电 压;z1,z2,y为 评 价信 号;Gn(s)为 基 准 被 控 对 象。

图4 混合灵敏度控制框图Fig.4 Block diagram by mixed sensitivity control
从参考信号w到误差信号e和输出信号v0的闭环传递函数分别为

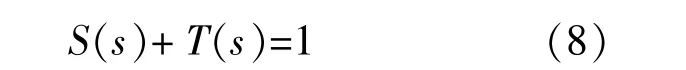
考虑加权混合灵敏度问题的基本结构如下:
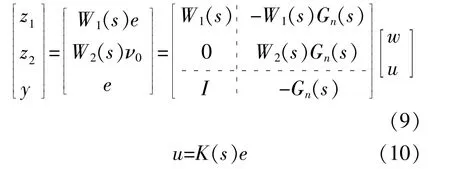
其中,广义受控对象的状态空间表达式为
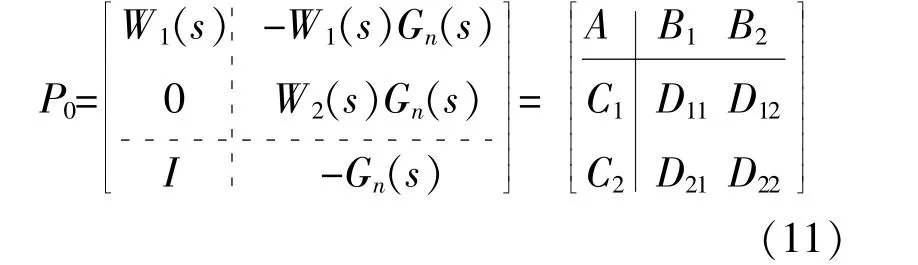
联 立 式(8)和 式(9),参 考 信 号w至 评 价 信 号z1,z2之间的闭环传递函数矩阵为

根据小增益定理,混合灵敏度设计问题可以表示为寻找实有理控制器K(s),使闭环系统稳定,且满足以下条件:

通常表示为
设计方法的关键是在频域内选择合适的加权函数W1,W2,使其满足闭环系统设计的多目标要求。鲁棒H∞控制器的具体设计步骤如下[19]:
①根据控制系统的特点设计合适的权重函数W1,W2;
②在鲁棒H∞标准框架下求取闭环系统的控制器;
③考虑控制器的实现问题,降低控制器K(s)的阶数,同时不降低控制器的性能。
2.2 电压环鲁棒H∞控制器设计
根据上述鲁棒H∞控制器设计步骤,首先设计W1(s)。灵 敏 度 函 数S(s)表 示 从 参 考 信 号w到系统误差信号e的传递函数。由式(14)可知,灵敏度 函 数S(s)的 形 状 可 以 由 权 重 函 数W1(s)来 调整,选择二阶函数作为权重函数W1(s)的函数类型[20]:
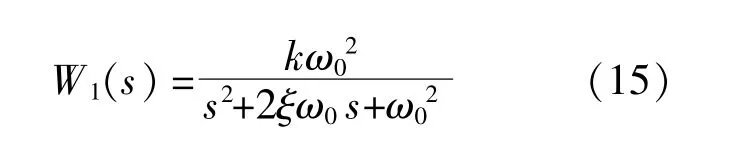
式中:k为比例系数;ω0为基波角频率;ξ为阻尼系数。
阻 尼 系 数 ξ越 小,则W1(s)的 峰 值 越 大,带 宽越窄。当阻尼系数x趋近于零时,所设计出的控制器性能类似于理想的谐振控制器,理论上可以在工频处实现零稳态误差。本文经过理论分析与仿真 对 照 后,选 择k=1,ω0=314 rad/s,x=0.01。
关 于 权 重 函 数W2(s)的 设 计,由 式(5)可 知:
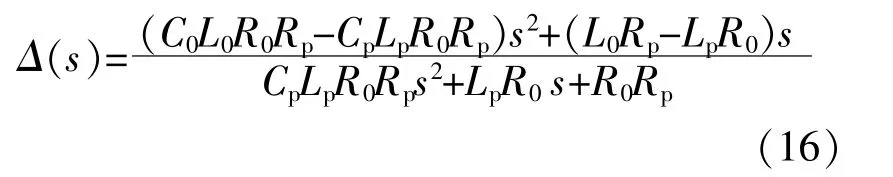
Δ(s)为多参数摄动引起的乘性摄动量。为了研究多参数摄动对摄动量 Δ(s)的影响,按照表1数据做出不同参数摄动情况下的 Δ(s)函数图像(图5)。

表1 参数摄动表Table 1 Multi-parameters perturbation
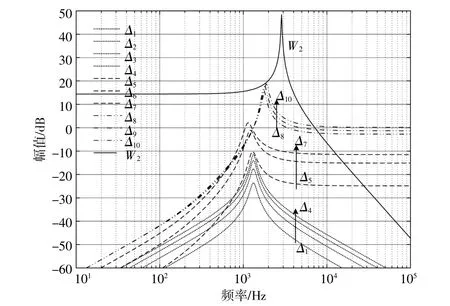
图5 参数摄动量Δ(s)与权重函数W2(s)Fig.5 PerturbationΔ(s)and weighting function W2(s)
图5所示为多种类型的系统参数同时偏离基准 值 时 的 摄 动 量 Δ(s)曲 线。对 比 Δ1(s)~Δ4(s)的 曲线可知,当电感和电容值不变时,随着电阻实际值与基准值的偏离程度不断增加,系统相对摄动量Δ(s)的峰值也在增加,对系统的稳定性影响越来越 大。对 比 Δ5(s)~Δ7(s)的 曲 线 可 知,当 电 容 和 电阻值不变时,随着电感实际值与基准值的偏离程度不断增加,系统相对摄动量 Δ(s)的峰值在增加,峰值点对应的频率也发生了明显的变化。对比Δ8(s)~Δ10(s)的 曲 线 可 知,当 电 感 值 和 电 阻 值 不 变时,随着电容实际值与基准值的偏离程度不断增加,系统相对摄动量 Δ(s)的峰值随之增加,峰值点对应的频率略微发生变化。
选择权重函数W2(s)时的具体要求:在一定频率范围内其数值在最大参数摄动量 Δ(s)之上。经综合对比,最终确定:
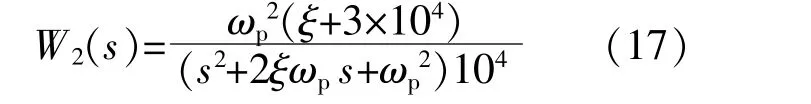
式 中:ω0=18 000;x=0.01。
采用Matlab鲁棒控制工具箱求取鲁棒控制器。考虑到控制器的实现问题,利用降阶函数对控制器进行降阶,降阶后的鲁棒控制器如下[21]:
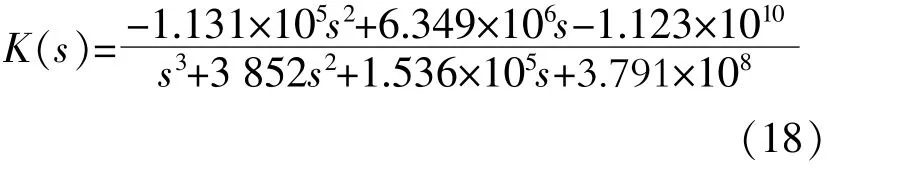
此外,针对鲁棒电压控制器阶数较高所造成系统响应速度慢的问题,本文增加了基于扰动观测器的负载电流前馈控制环节。
2.3 基于扰动观测器的负载电流前馈控制
基于扰动观测器的负载电流前馈控制结构图如图6所示。其中:Vref(s)为孤岛微网逆变器的参考电压输入;Vo(s)为微网逆变器的输出信号,即负载电压;G(s)为微网逆变器的实际模型;Gn(s)为 微 网 逆 变 器 的 标 称 模 型;D(s)为 系 统 的 等 效外部扰动,在本文中主要将负载电流造成的影响视 作 扰 动;ξ(s)为 传 感 器 噪 声;Q(s)为 低 通 滤 波器;K(s)为控制系统中电压环的鲁棒控制器。
根据图6可得不加扰动观测器时微网逆变器的输入输出关系:
其中:
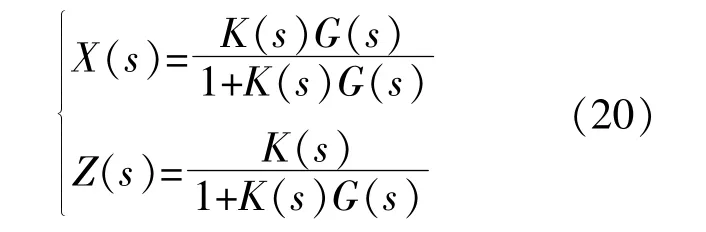
根据图6可得到加入扰动观测器后微网逆变器的输入输出关系如下:
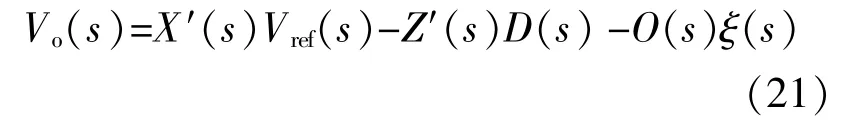
其中:
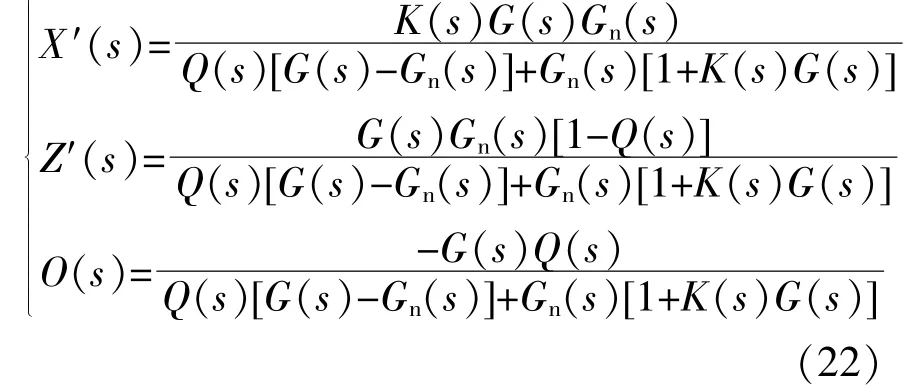
在 式(22)中,当Q(s)=1时,微 网 逆 变 器 的 输入输出关系如下:

在 式(22)中,当Q(s)=0时,微 网 逆 变 器 的 输入输出关系如下:

式(23)表 明,当Q(s)=1时,微 网 逆 变 器 的 输出信号不受电流扰动的影响,但是受到传感器噪声 的 影 响 更 敏 感。式(24)表 明,当Q(s)=0时,微网逆变器的输出信号不受传感器噪声的影响,但是受到低频电流扰动的影响。综上所述,可以将Q(s)设计为低通滤波器,使其在高频段具有良好的噪声抑制能力,在低频段具有对扰动电流的抑制 能 力[22],[23]。
设计低通滤波器的形式如下:
式中:τf为滤波器的时间常数。
为了满足扰动观测器在物理上的实现,k与j的关系应满足k-j>m-l;而且考虑到滤波器的延时问题,k-j的值越小越好[24]。根据微网逆变器系统的特点可知,被控对象为二阶系统,可选用二阶形式的低通滤波器:
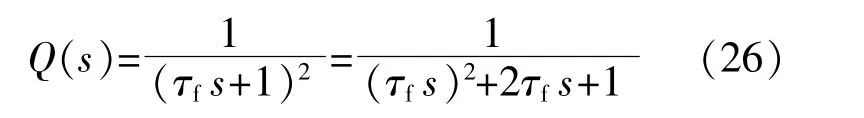
采用带有扰动观测器的鲁棒双环控制器,鲁棒电压外环能够在预设的参数摄动范围内维持系统的稳定,并保持很小的稳态误差。这是由于设计鲁棒电压环时选定的权重函数W1(s)为谐振形式。在实际的微网逆变器系统中,当负载切换时,存在因负载切换而产生的电流扰动,通过设定电流扰动观测器来补偿负载电流扰动。
2.4 灵敏度对比分析
微网逆变器系统不加扰动观测器时,系统的闭环传递函数关于滤波电容的对数灵敏度关系为
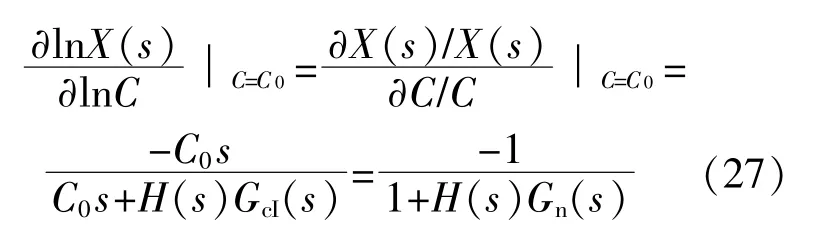
微网逆变器系统加入扰动观测器时,系统的闭环传递函数关于滤波电容的对数灵敏度关系为
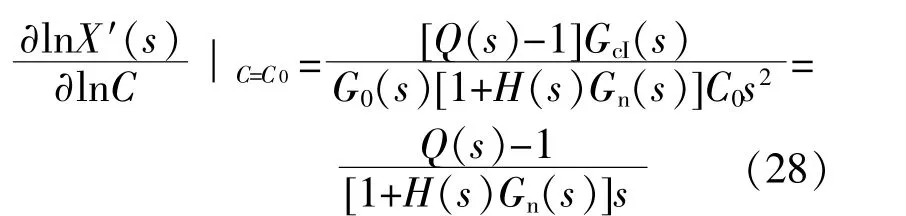
根据式(27)可以画出不加扰动观测器时传递函数X(s)关于滤波电容的对数灵敏度伯德图。根据式(28)可以画出加扰动观测器后传递函数 关于滤波电容的对数灵敏度伯德图。微网逆变器系统不加扰动观测器和加扰动观测器的灵敏度对比如图7所示。

图7 传递函数关于滤波电容的灵敏度伯德图Fig.7 Bode diagram of transfer function on capacitance sensitivity
由图7可知,在1 Hz~100 kHz的频段内,加入扰动观测器之后的微网逆变器灵敏度幅频特性曲线向下移动。这表明当滤波电容值发生变化时,系统的传递函数受到的影响变小,微网逆变器的抗扰动能力变强。
3 仿真与实验
为了验证本文所提出控制策略的真实性和有效性,在Matlab/Simulink环境下对孤岛微网逆变器进行仿真,并在2 kVA的逆变器样机上进行实验。本文设计的微网逆变器总体结构如图8所示。

图8 微网逆变器总体结构图Fig.8 Overall configuration of inverter in isolated microgrids
逆变器采用带有LC型滤波器的单相全桥拓扑。全控型器件采用IGBT,直流侧电压由大功率直流电压源提供。负载电阻采用多个铝壳式电阻串并联的方式连接,用空气开关对负载进行切换。仿真与实验的主要参数设置如表2所示。
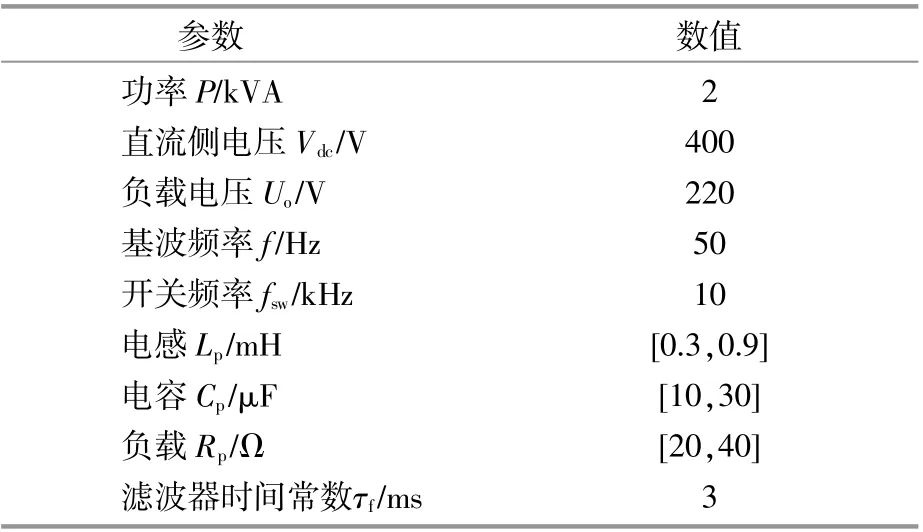
表2 系统参数Table 2 System parameters
3.1 仿真结果与分析
系 统 的 仿 真 结 果 如 图9所 示。图9(a)~(c)依次为微网逆变器的电压环控制器采用PI控制策略、无观测器鲁棒控制策略和有观测器鲁棒控制策略的负载电压和负载电流波形图。负载性质为阻感性负载。


图9 系统带阻感性负载时的仿真结果Fig.9 Simulation results with resistive-inductive load
从图9(a)可见,系统稳态运行时,采用PI控制策略的微网逆变器输出电压和电流有较多的谐波,波 形 发 生 畸 变;图9(b),(c)中 的 逆 变 器 输 出的电压和电流几乎没有发生波形畸变,波峰位置也相对平滑。通过3个图的对比可知,带有鲁棒电压控制器的微网逆变器系统具有更好的稳态性能;观测器的加入与否对系统的稳态性能没有影响,不影响系统的稳定运行。
图10为微网逆变器负载切换时输出的电压与 电 流 波 形。图10(a)~(c)依 次 为 微 网 逆 变 器 的电压环控制器采用PI控制策略、无观测器鲁棒控制策略和有观测器鲁棒控制策略的负载电压和负载电流波形图。负载切换情况:t=0.065 s时,负载由P=1 kW切换至P=2 kW;t=0.125 s时,负载由P=2 kW切换至P=1 kW。

图10 负载切换时的仿真结果Fig.10 Simulation results with load switching
从图10(a)可以看出,当负载增加时,采用PI控制策略的微网逆变器输出电压跌落明显,从311 V迅速跌落至260 V左右,跌落幅度接近50 V;在电压回升阶段,电压波动也表现得较为明显。当负载功率突然减小时,逆变器输出的电压幅值迅速增大,达到350 V,增幅接近40 V,且恢复缓慢。图10(b)所示的电压环控制器采用无扰动观测器的鲁棒控制策略,在负载功率增大和减小的过程中,电压跌落和上升幅度不超过20 V。图10(c)显示,当负载切换时,逆变器输出的电压波动最小。虽然负载切换对逆变器输出电压有一定的影响,但是波峰位置相对平滑,没有陡升或者陡降 现 象。对 比 图10(a)~(c)可 见,采 用PI控 制 策略的逆变器在负载扰动抑制方面的表现性能不佳,在负载切换时,其输出电压的波动幅度超出20%;采用鲁棒控制策略的逆变器在负载切换时,其电压波动在10%以内,加入扰动观测器后,逆变器输出的电压的波动幅度非常小。这表明扰动观测器对负载切换产生的扰动具有较好的抑制能力。
3.2 实验结果与分析
系统带阻感性负载时的实验结果如图11所示。图11(a),(b)分 别 为 孤 岛 微 网 逆 变 器 带 阻 感性负载时,电压环控制器采用PI控制策略和带扰动观测器的鲁棒控制策略下的输出电压波形和电流波形。
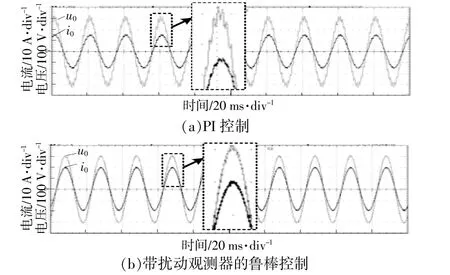
图11 系统带阻感性负载时的实验结果Fig.11 Experimental results with resistive-inductive load
从图11(a)可以看出,当电压环控制器采用PI控制策略时,系统的输出电压波形波峰位置存在明显畸变,与图10(a)的仿真结果一致。采用带扰动观测器的鲁棒控制策略时,孤岛微网逆变器输出电压波形变得平滑,波峰位置没有畸变现象出现,与图10(c)所对应的仿真结果一致。图11表明了带有扰动观测器的鲁棒控制策略能够提高系统的稳态性能。
图12给出了多参数摄动时系统的实验结果。其 中,图12(a),(b)分 别 为 采 用PI控 制 策 略 和 带扰动观测器的鲁棒控制策略。
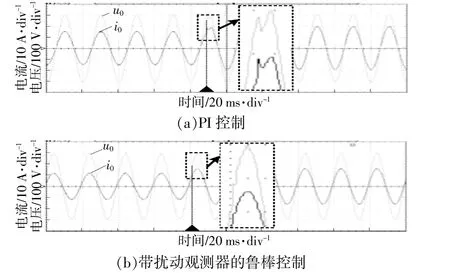
图12 多参数摄动时系统的实验结果Fig.12 Simulation results with load variation
该实验条件是在系统运行过程中改变系统的电容。从图12中可以看出,当系统的电容参数发生变化时,PI控制下的逆变器输出电压发生明显跌落,而带有扰动观测器的鲁棒控制下的逆变器输出电压波形几乎没有发生跌落。这说明带有扰动观测器的鲁棒控制器对于系统的电容参数变化具有一定的鲁棒性;系统对于电容参数变化的灵敏度较小,当电容参数变化时,对系统的稳态性能影响小。
4 结论
本文针对孤岛微网逆变器系统的内部参数摄动和负载扰动进行了理论建模。在设计加权函数时,将内部参数摄动和负载扰动的范围考虑在内;通过混合灵敏度分析法设计鲁棒H∞控制器并对其进行降阶,实现了对输出电压的精确跟踪。实验结果表明,当系统发生参数摄动和负载突变时,鲁棒H∞控制器仍然能够维持系统的稳定性,并保持所期望的稳态性能。扰动观测器可以抑制因负载功率切换而导致的电压突变,同时也能够降低系统的输出电压对参数摄动的灵敏度,在一定程度上提高了孤岛微网逆变器系统的快速性和鲁棒性。

