电动汽车电机驱动系统传导干扰建模及预测

刘松林，杨天矾，支永健，闵建军

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

电机驱动系统作为电动汽车上高电压、大电流且耦合路径多样的电气系统，其中的功率器件工作时，快速变化的电流和电压会通过分布电感和电容产生高幅值、宽频带、以传导为主的电磁干扰，给电动汽车的安全运行带来隐患。通过建立电机驱动系统EMI仿真模型，不仅能实现对系统传导干扰的精确预测，而且有利于在系统设计阶段进行电磁兼容优化，特别是EMI滤波器设计。文献[1]的研究结果表明，在一个三相逆变器中，如果对每个元件及其耦合效应都进行精确建模，那么在100 MHz以下频率范围内，EMI仿真预测结果都是准确的。然而在实际工程中，EMI预测通常只能保证5 MHz以下频率范围内的预测误差小于6 dB[2-6]，而高频误差可能会达到20 dB以上。这种误差主要由以下几方面因素引起：

（1）电机高频建模误差较大。一般基于物理结构的电机高频建模需要通过阻抗测量或者有限元分析（FEA）来提取多个未知物理量[7]，然而由于电机物理结构过于复杂，很难将所有参数量化，需要根据不同物理量在不同频段的主导地位进行局部建模[8]，因此难以保证全频段的模型误差。文献[5-6]将电机作为黑盒进行行为级高频建模，但都是基于某些特定频率建立数值拟合方程进行迭代优化，在这些特定频率下模型精度非常高，但在其他频率范围内模型误差较大。

（2）系统干扰源建模误差较大。文献[9]利用双重傅里叶积分方法在频域中建立了理想的逆变器SPWM共模干扰源和差模干扰源，在此基础上考虑PWM上升沿影响，叠加了一个上升沿优化函数，再通过反傅里叶变换到时域进行仿真。采用这种方法是假定每个PWM方波的上升沿时间相等，并且需要提前进行IGBT双脉冲试验以获取PWM上升沿时间，这与实际情况存在一定差异。文献[2-6]采用时域提取的方法通过测试得到逆变器共模和差模干扰时域波形，通过戴维南等效定理建立等效干扰源和源阻抗模型，这种方法较为普遍使用，但受限于测试采集设备的A/D转换精度，一般情况下，频率在10 MHz以上的采集信号会被设备底层的噪声所淹没。

（3）时域仿真结果经傅里叶变换后误差较大。电动汽车电机驱动器传导发射水平是以直流输入侧线路阻抗稳定网络（line impedance stabilization network, LISN）端EMI接收机输出结果为评判依据，但由于EMC标准[10]对接收机的分辨率带宽（RBW）、包络检测器、峰值检测器、准峰值检测器和平均检测器有特定的要求，若不考虑这些要求，快速傅里叶变换（FFT）结果可能与实际测量结果不符[11-12]。

本文采用矢量匹配算法建立了电机行为级模型，在150 kHz～100 MHz频段内模型误差小于1%。矢量匹配算法被广泛应用于电力系统的频率特性拟合[13]，不需要经验丰富的用户选择拟合频率点，其拟合结果在所有相关频率范围内都与测量结果相匹配，并且电路拓扑等效方法比较成熟，参数化方法相对简单。在电机精确建模的基础上，再通过时域提取，建立了系统干扰源等效模型，最后搭建了整个电机驱动系统的高频传导干扰仿真电路，分别预测了系统高压直流输入侧有EMI滤波器和无EMI滤波器时LISN上传导干扰电压大小。预测结果与实际测量结果在150 kHz～10 MHz频段内误差小于6 dB，验证了本文建模方法的正确性。

1 电机驱动系统传导干扰路径分析

电机驱动系统共模干扰主要由开关过程中瞬时跳变电压和系统内部寄生电容相互作用而产生。寄生电容包括IGBT对散热器寄生电容（CA,CB,CC）、直流母排对散热器寄生电容（CBUS）、电机绕组对机壳寄生电容（CMOTOR）以及线缆对屏蔽层寄生电容（CCable）等。系统共模传导干扰路径如图1中虚线所示，主要包括：①IGBT→三相屏蔽线→CMOTOR→接地板→CBUS→IGBT，即红色虚线路径；②IGBT→三相屏蔽线→CCable1→接地板→CBUS→IGBT，即蓝线色虚线路径；③IGBT→CA/B/C→接地板→LISN→直流屏蔽线→IGBT，即绿色虚线路径；④IGBT→CA/B/C→接地板→CCable2→直流屏蔽线→IGBT，即紫色虚线路径。图1中，CIN为直流支撑电容。

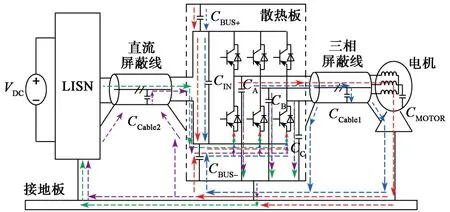
图1 共模传导干扰路径Fig. 1 Common mode EMI conducted path

电机驱动器差模干扰是由开关器件在开通和关断过程中产生的di/dt与系统中杂散电感相互作用形成的。若开关K1,K4,K6导通，系统差模传导干扰路径如图2中虚线所示，主要包括电源侧干扰路径（蓝线）和电机侧干扰路径（红线）。

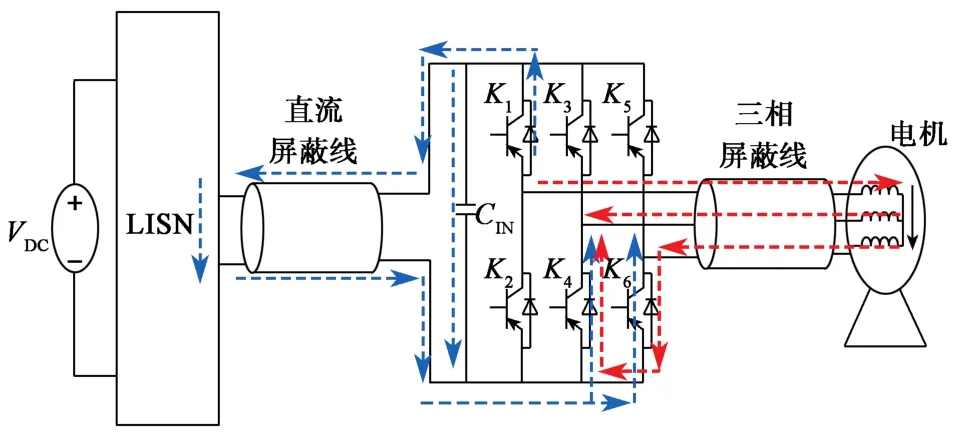
图2 差模传导干扰路径Fig. 2 Defferential mode EMI conducted path

2 电机驱动系统传导干扰电路建模

电机驱动系统传导干扰建模主要包括4个部分：系统干扰源建模、IGBT寄生参数提取、人工电源网络建模以及电机高频建模。

2.1 系统干扰源模型

电机驱动系统三相二电平逆变器拓扑如图3(a)所示，其中CBUS+和CBUS-分别为直流正负母排对散热器的寄生电容，ZMOTOR为电机绕组对机壳的寄生阻抗。通过测试将交流输出母排对直流负母排电压进行时域提取并表示为电压源，则可用图3(b)所示电压源来替换图3(a)中交流输出母排和直流负母排之间的IGBT开关。

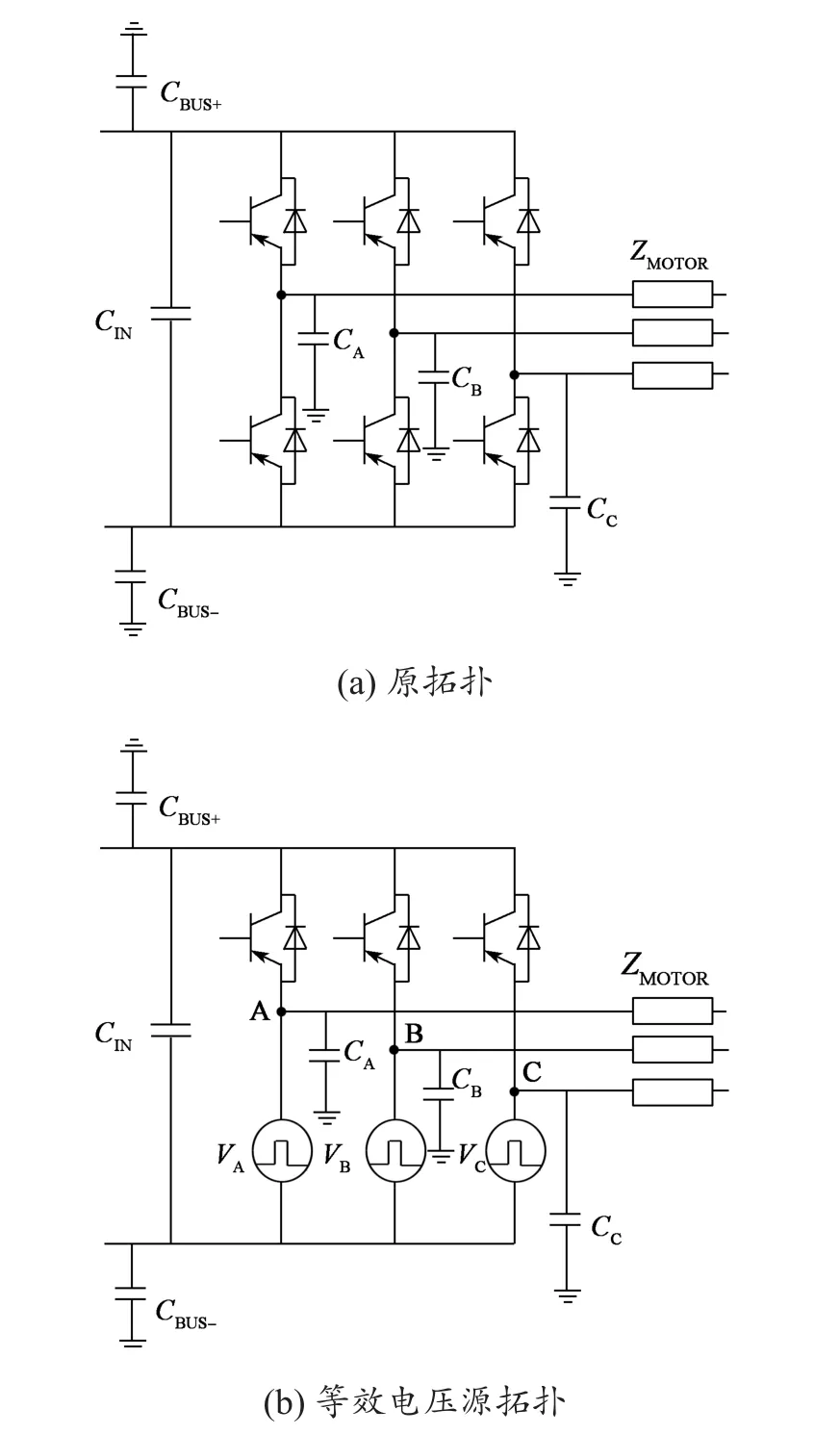
图3 三相二电平逆变器等效电压源拓扑Fig. 3 Equivalent voltage source topology of three-phase twolevel inverter

图4示出单相共模等效电路推导示意。在图4(a)所示的单相电路中，由于上开关与下开关总是同时动作，因此去除上管将不会影响图4(b)所示电路的功能。考虑到直流支撑电容CIN为差模电容，因此该支撑电容可以忽略，其共模等效电路如图4(c)所示。

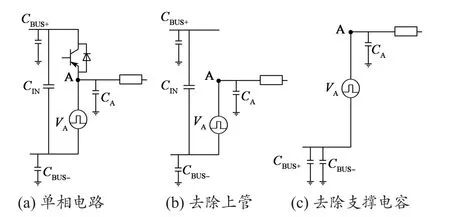
图4 单相共模等效电路推导Fig. 4 Derivation of single phase common mode equivalent circuit

同理，三相共模等效电路如图5所示。

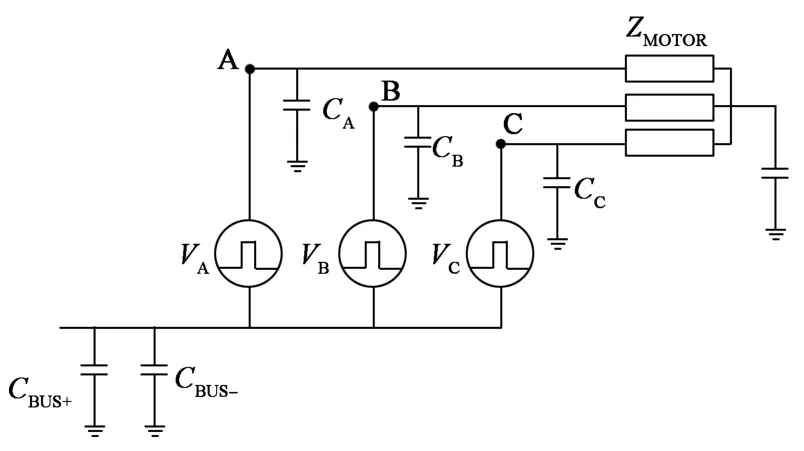
图5 三相共模等效电路Fig. 5 Equivalent three-phase common mode circuit

由电路叠加定理和戴维南等效定理可知，系统共模总干扰电压由每一相电压源电压叠加得到，如图6(a)所示，其计算见式(1)。考虑到三相交流输出母排结构对称，其对地寄生电容大小相等，因此整个三相二电平逆变器共模等效电路如图6(b)所示。

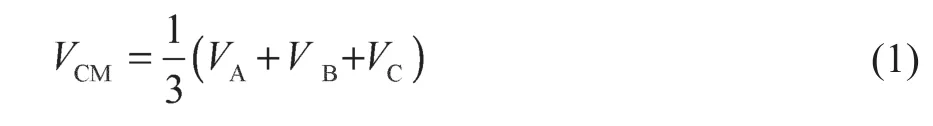
式中：VA,VB和VC为测量得到的单相电压值。

图6 三相二电平逆变器最终共模等效电路Fig. 6 Final common mode equivalent circuit of three-phase two-level inverter

采用宽频带电压探头（200 MHz）提取各相电压源，测量点位置为单相交流输出母排对直流负母排，如图7所示。根据Shannon定理，将示波器采样频率设置为50 MHz，可提供25 MHz带宽的有效数据，提取的电压源将被用于时域仿真。

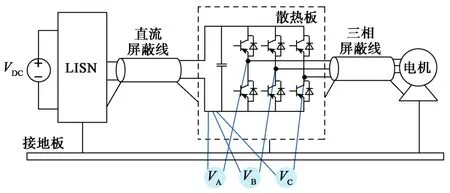
图7 单相电压源测量示意图Fig. 7 Schematic diagram of voltage source measurement for each phase

测量得到的每一相电压源电压再利用式(1)进行计算，可以得到系统共模等效干扰源电压VCM，其时域波形如图8所示。

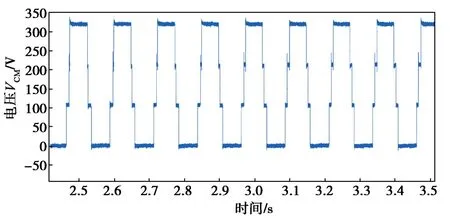
图8 系统等效共模干扰源VCM时域波形Fig. 8 CM interference source VCM waveform of the system in time domain

系统等效差模干扰源电压VDM被定义为逆变器输出线电压，即输出相电压差。以AB两相为例，等效差模干扰源电压表达式为

等效差模干扰源建模过程与共模干扰源的类似，这里不再具体介绍，其通过测量提取后的时域波形如图9所示。

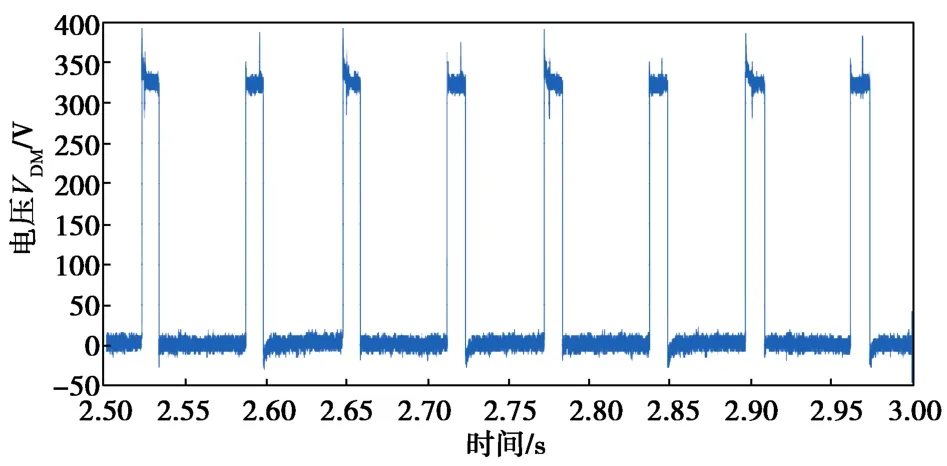
图9 系统等效差模干扰源电压VDM时域波形Fig. 9 DM interference source voltage waveform of the system in time domain

2.2 IGBT寄生参数提取

由于IGBT的衬底（金属）与逆变器的散热片之间存在寄生电容，IGBT快速通断造成高dv/dt，引起的高频电流分量会通过这些电容进入接地板。此外，直流母排和散热片之间的寄生电容也将为共模噪声提供通道。因此，寄生电容的参数化对逆变器系统的建模具有重要意义，这些电容参数将基于IGBT模块的阻抗测试进行提取。逆变器的IGBT模块和单相3D模型如图10所示。

图10 IGBT模块和单相三维模型Fig. 10 IGBT module and its single-phase three-dimensional model

如图11所示，蓝色、红色和绿色基板分别为直流正母排、直流负母排以及交流输出母排。建模时需要提取这些基板对地的寄生电容，直接测量这些电容是不准确的，因为开关的结电容会参与测量，使测量结果大于其实际值。

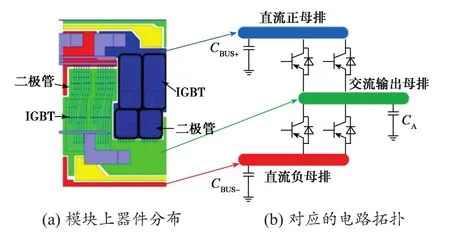
图11 IGBT模块寄生电容示意图Fig. 11 Schematic diagram of parasitic capacitance of IGBT module

断开IGBT的发射极与交流输出母排和直流负母排的连接（图12），直接测量直流正母排、直流负母排和交流输出母排对地寄生电容，这样可以消除IGBT开关结电容的影响。采用阻抗分析仪测量寄生电容，测量结果见表1。

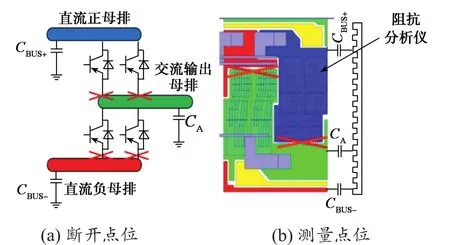
图12 IGBT模块的寄生电容测量Fig. 12 Parasitic capacitance measurement of IGBT module

表1 IGBT模块寄生电容测量结果Tab. 1 Measurement results of parasitic capacitance of IGBT module

2.3 屏蔽线缆模型

以三相屏蔽线缆为例，其单位长度的多导体传输线模型如图13(a)所示。图中，R是线缆内导体单位长度电阻，L是内导体单位长度电感，C表示内导体单位长度对屏蔽层电容，Lm和Cm分别表示两内导体间单位长度的互感和互容。考虑到每相线缆都有屏蔽层，故相间线缆互容为零，且线缆相间距离较大（50 mm以上），导体互感远小于自感，因此三相屏蔽线缆多导体传输线模型可被简化为图13(b)所示模型。

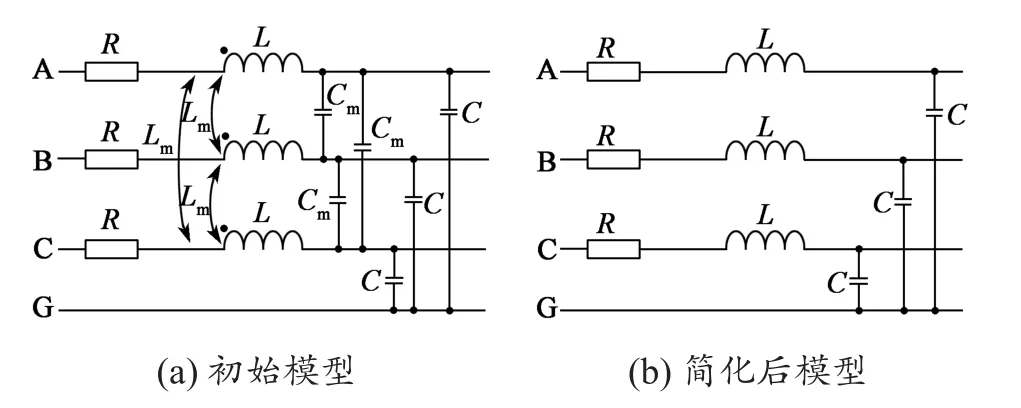
图13 三相屏蔽线缆多导体传输线模型Fig. 13 Multi-conductor transmission line model of threephase shielded cable

为确定三相屏蔽线缆模型参数，采用阻抗分析仪对每相屏蔽线缆进行开路和短路测试。线缆自感和线缆对屏蔽层寄生电容的计算如下：

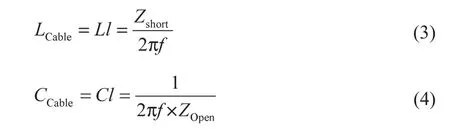
式中：LCable——线缆总电感；CCable——线缆对屏蔽层总电容；l——线缆长度；f——测量频率；ZShort——短路测量阻抗；ZOpen——开路测量阻抗。

基于上述测量方法与计算方法，可以得到图13(b)中所有电路参数，如表2所示。

表2 三相屏蔽线缆电路参数Tab. 2 Circuit parameters of three-phase shielded cable

根据三相线缆电路参数在共模电路和差模电路中的串并联关系，可以分别得到共模和差模电路模型（图14）。

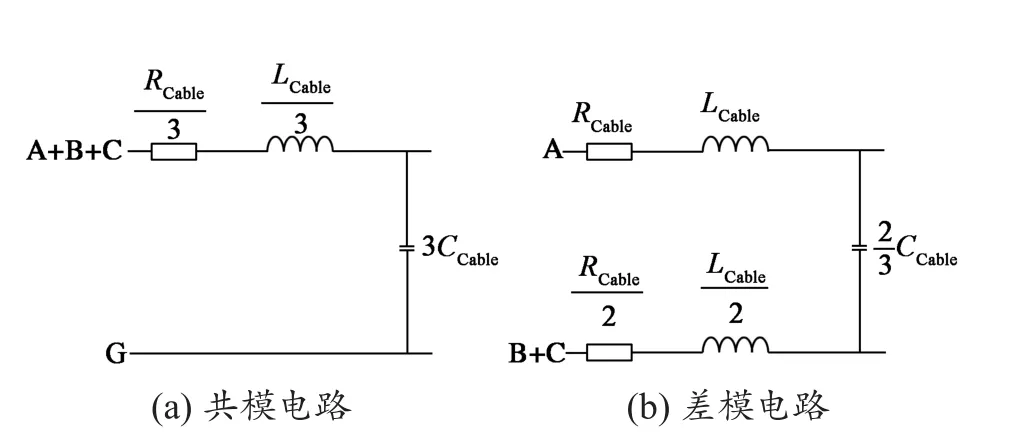
图14 三相屏蔽线缆共模和差模电路模型Fig. 14 Common mode and differential mode circuit models of three-phase shielded cable

2.4 LISN模型

LISN是电机驱动器传导干扰测量过程中必不可少的设备，其主要作用在于：在一定频率范围内提供稳定的50 Ω阻抗；将供电电源与被试设备（EUT）隔离；将被试设备产生的电磁干扰耦合到EMC接收机上，以便于测量。本文所研究系统采用的LISN其频率范围为100 kHz～150 MHz，LISN的电路参数可以通过查阅厂家技术手册得到（图15）。

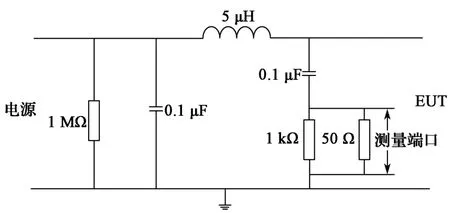
图15 LISN电路Fig. 15 LISN circuit

在共模电路中，系统中两个LISN是并联结构，其简化模型如图16(a)所示；在差模电路中，两个LISN则是串联结构，其简化模型如图16(b)所示。

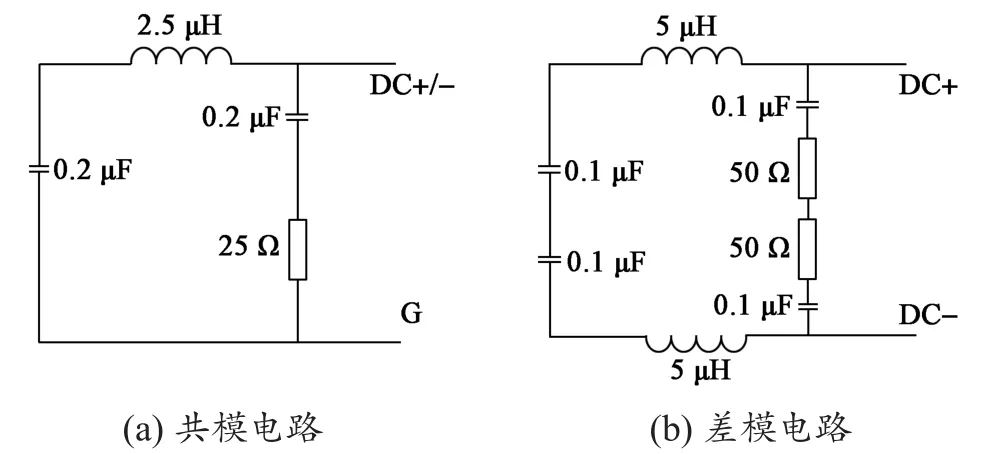
图16 LISN共模和差模电路模型Fig. 16 Common mode and differential mode circuit models of LISN

2.5 电机模型

电机作为驱动系统传导干扰流经的重要路径，其高频模型的精度影响所搭建的系统传导干扰预测模型的准确性。然而，目前电机高频建模往往基于电机的物理结构，建模过程复杂、模型参数误差大、通用性差且模型频带覆盖范围窄。为此，本文采用一种基于矢量匹配法的电机行为级建模方法，其将电机当作“黑盒”处理，不需要考虑电机内部复杂结构的实际物理意义，特别适合对电机阻抗的频变效应进行拟合建模。

采用图17所示的阻抗测量方法分别对电机共模和差模阻抗进行测试，其中共模阻抗幅值和相位的测量结果如图18所示，差模阻抗幅值和相位的测量结果如图19所示。

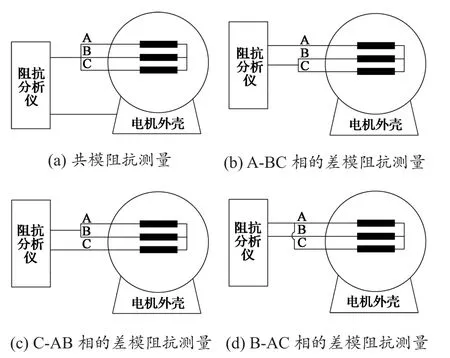
图17 电机共模和差模阻抗测量Fig. 17 Measurement of common mode and differential mode impedance of motor

图18 电机共模阻抗幅值和相位测试结果Fig. 18 Test results of common mode impedance amplitude and phase of motor

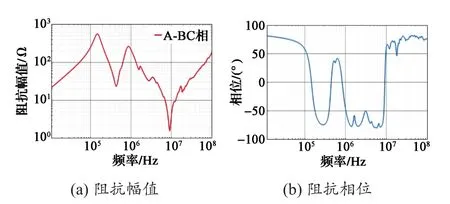
图19 电机差模阻抗幅值和相位测试结果Fig. 19 Test results of differential mode impedance amplitude and phase of motor

首先将共模阻抗测试数据近似为一个多阶网络函数形式，见式(5)。网络函数阶数n越大，拟合精度越高，同时电路建模复杂程度越高。

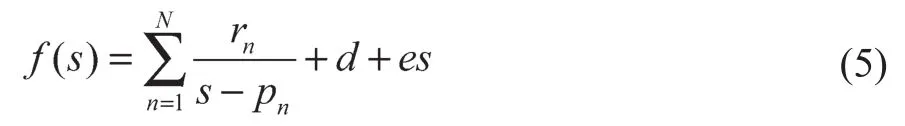
式中：f(s)为共模阻抗测试的离散数据；s为复频率；留数rn和极点pn为实数或共轭复数对；d和e为实数。

未知参量rn,pn,d和e通过矢量匹配法[11]求解后，可以将网络函数转化为相应的等效电路。综合考量计算精度与建模复杂度后，所选择的等效电路为一个8阶Foster并联网络模型（图20）。

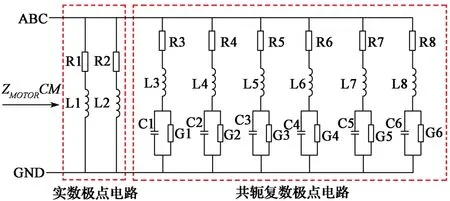
图20 电机共模等效电路模型Fig. 20 Model of equivalent common mode circuit for motor

图20中，电阻、电感串联形式的实数极点电路被用来等效式(5)中极点和留数为实数时的函数项，电阻与电感参数的计算公式如下：

图20中，电阻、电感、电容及电导组合形式的共轭复数极点电路被用来等效式(5)中极点和实数为共轭复数的函数项，参数计算公式如下：

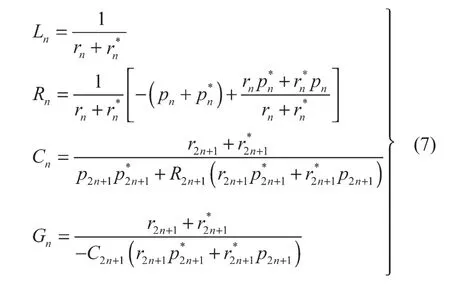
本文计算结果中不包含常数项d和一次项es，因此不需要进行电路转换。

电机共模等效电路模型中各元件参数最终计算结果见表3。

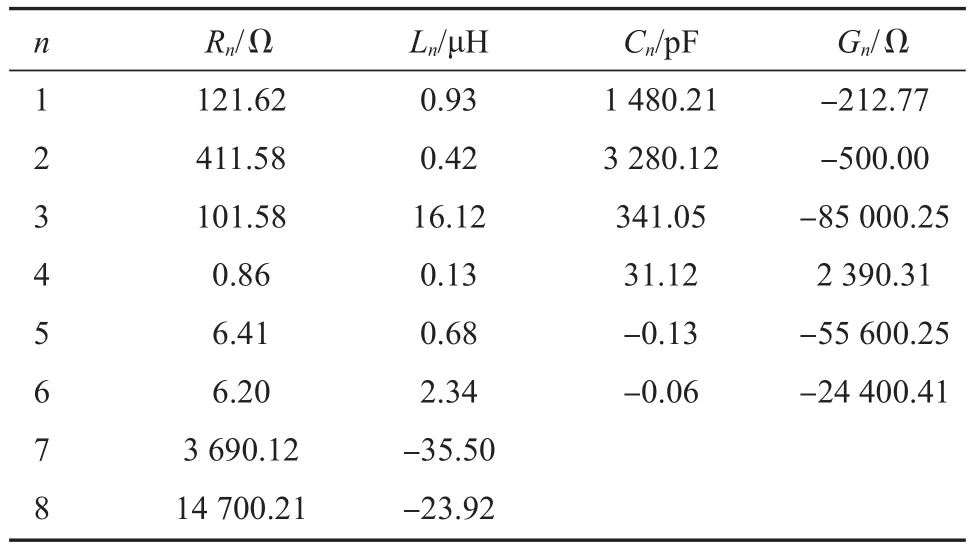
表3 电机共模等效电路模型参数Tab. 3 Parameters of common mode equivalent circuit model for motor

在电路仿真软件中对图20所示电机共模等效电路模型进行阻抗仿真计算，仿真结果与实际测试结果对比如图21所示。

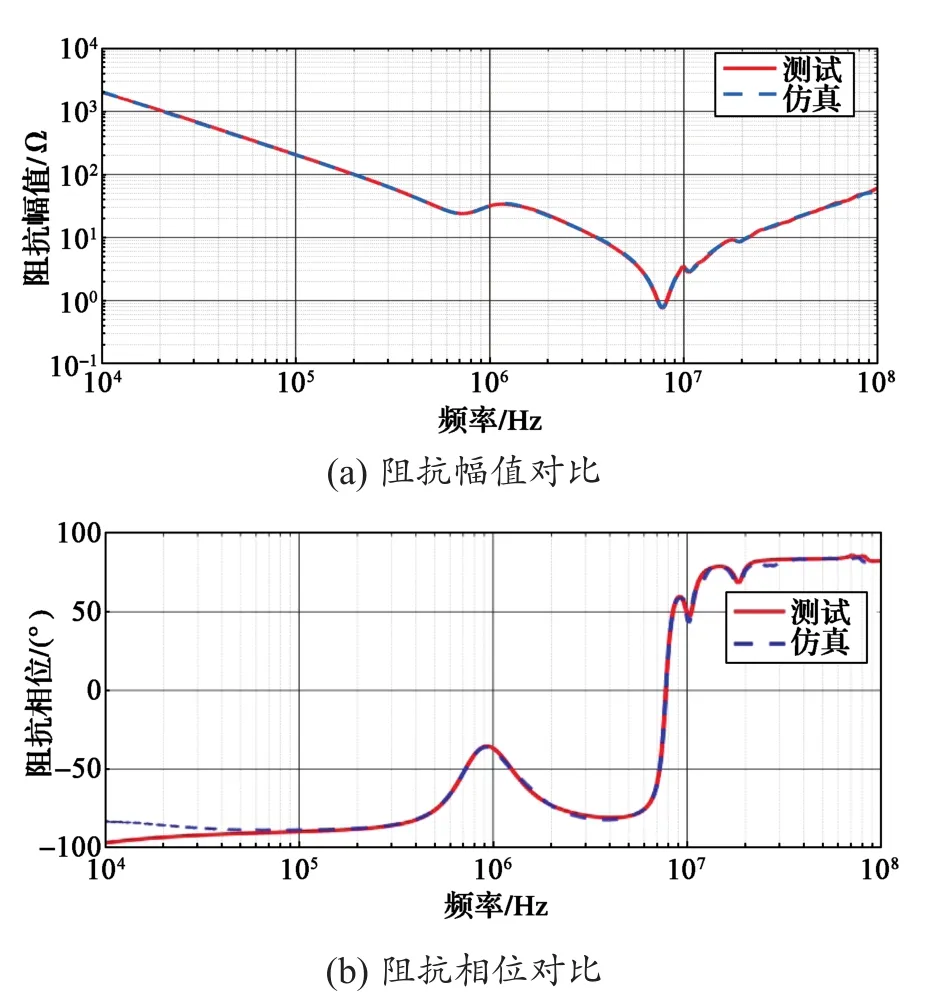
图21 共模阻抗仿真值和测试值对比Fig. 21 Comparison between simulation and test values of common mode impedance

从图21对比结果中可以看出，本文根据矢量匹配法建立的电机共模高频电路模型阻抗仿真结果与实际测试结果一致性非常高，在10 kHz～100 MHz频段范围内仿真结果准确度约达到100%，基本消除了电机高频建模误差对后续系统级高频传导干扰仿真的影响，极大地提高了系统级仿真预测准确度。

同理，基于矢量匹配法建立电机差模等效电路模型后在电路仿真软件中进行阻抗仿真计算，仿真结果与实际测试阻抗幅值和相位对比如图22所示。

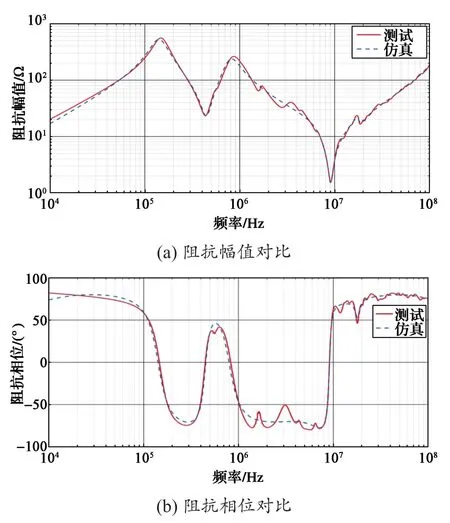
图22 差模阻抗仿真值和测试值对比Fig. 22 Comparison between simulation and test values of differential mode impedance

图22中，电机差模阻抗测试曲线存在较多谐振点，增加了基于矢量匹配法电路建模的难度，因此模型仿真误差大于共模模型误差。但就整体而言，在10 kHz～100 MHz频段范围内，电机差模等效电路模型的建模误差依然可以忽略，能够保证后续系统级差模传导干扰仿真的准确性。

3 系统仿真预测与实验验证

3.1 系统仿真预测模型

基于前述电机驱动器各部件传导干扰电路建模过程，建立如图23所示的系统共模传导干扰和差模传导干扰高频电路模型，仿真预测端口为LISN上共模电压VSimCM和差模电压VSimDM。

图23 系统传导仿真电路模型Fig. 23 System conduction simulation models

3.2 实验验证

为验证本文系统传导仿真模型的预测准确性，以一台电动汽车实际电机驱动器为对象进行实验测试（图24），测试端口为高压直流输入端。驱动器直流输入电压为320 V，开关频率8 kHz，电动机运行工况为空载模式，转速1 000 r/min，测试分辨率带宽为9 kHz，检波方式为峰值检波。

图24 电机驱动系统传导干扰试验台位布置Fig. 24 Layout of conductive interference test bench for motor drive system

图25和图26示出系统直流输入端无EMI滤波抑制情况下LISN上共模和差模干扰电压仿真与测试结果对比。利用仿真模型对LISN的共模干扰进行预测，在150 kHz～10 MHz频段内，预测误差小于6 dB，在该频段表明所设计的传导仿真模型具备定量评估预测能力；频率超过10 MHz，误差将增大，可以进行干扰趋势性预测。利用仿真模型对LISN差模干扰进行预测，在150 kHz～20 MHz频段内，预测误差小于6 dB，表明所设计的传导仿真模型具备定量评估预测能力。

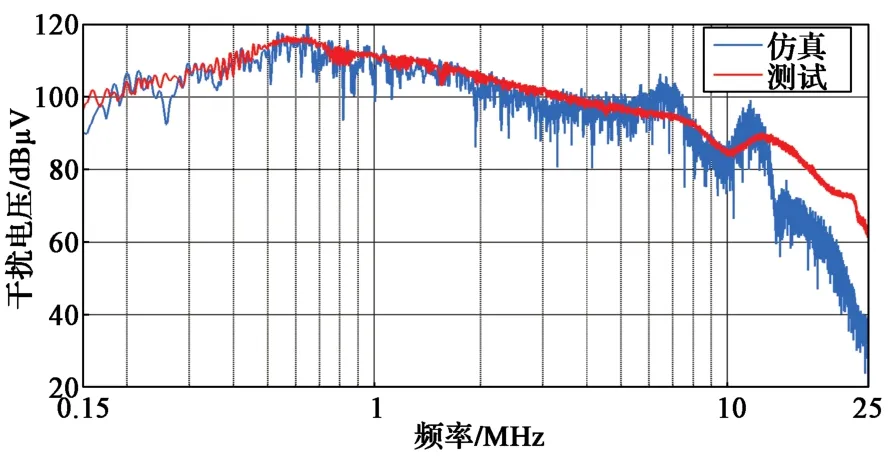
图25 无EMI滤波时LISN上共模干扰电压仿真值和测试值对比Fig. 25 Comparison between simulation and test results of common mode voltage on LISN without EMifilter

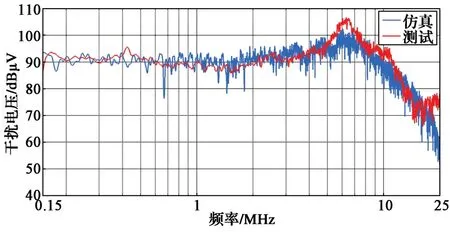
图26 无EMI滤波时LISN上差模干扰电压仿真值和测试值对比Fig. 26 Comparison between simulation and test results of differential mode voltage on LISN without EMifilter

在驱动器高压直流输入侧加装一个如图27所示的EMI滤波器，测试LISN上共模和差模干扰电压的抑制情况，以验证仿真模型对EMI滤波抑制效果的预测能力，这样有利于指导对系统EMI滤波器的正向设计。对EMI滤波器建模时，主要需考虑电容等效寄生电感和电阻的提取以及基于共模电感阻抗频变特性的等效电路的建模问题，具体建模过程这里不再介绍。

图27 EMI滤波器安装示意图Fig. 27 EMifilter installation diagram

图28和图29示出系统直流输入端加装EMI滤波器后的LISN上共模和差模干扰电压仿真与测试结果对比。可以看出，在150 kHz～10 MHz频段范围内，仿真模型可以对EMI滤波器的共模抑制进行定量预测，整体误差小于6 dB；在150 kHz～3 MHz频段范围内，仿真模型可以对EMI滤波器的差模抑制进行定量预测，整体误差小于6 dB，但预测频率上限还需提高。综合考虑，由于EMI滤波器设计难点在于共模电路，因此本文提出的基于电机驱动器的传导仿真模型基本具备了指导系统电磁兼容正向设计的能力。

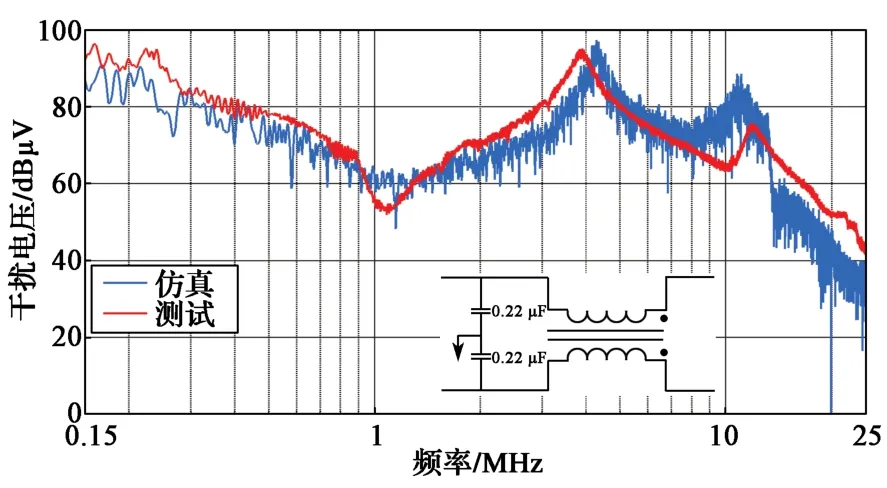
图28 加EMI滤波器后LISN上共模干扰电压仿真与测试对比Fig. 28 Comparison between simulation and test results of common mode voltage on LISN with EMifilter

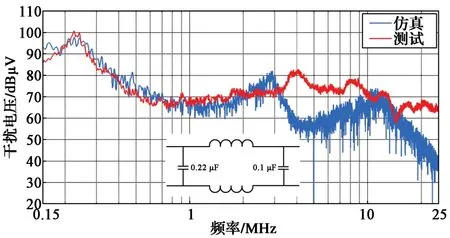
图29 加EMI滤波器后LISN上差模干扰电压仿真与测试对比Fig. 29 Comparison between simulation and test results of differential mode voltage on LISN with EMifilter

4 结语

为解决电动汽车电机驱动系统高压直流端电磁干扰风险定量评估问题，本文建立了一套系统级共模和差模传导干扰仿真预测电路模型，提出了基于矢量匹配法的电机高频电路等效建模方法和基于时域提取的系统干扰源等效建模方法。其在150 kHz～10 MHz 频段内保证了模型仿真预测的精准度，具备了对系统传导干扰的定量预测能力和对电磁干扰抑制方案（EMI滤波）的风险评估能力，基本达到了指导系统级电磁兼容设计的效果。

本文所提模型在10 MHz以上频段时仿真误差较大，无法对系统电磁干扰做到定量预测评估，只能进行趋势性分析。该问题一方面可能是由干扰源在进行时域提取时测试设备采集精度不足造成，无法有效采集到10 MHz以上微弱的电压信号；另一方面可能是由于IGBT或屏蔽电缆高频寄生参数建模误差而造成。后续将针对这两方面进行深入研究，以提高模型定量预测的频率上限，使之不低于30 MHz。另外，本文只研究了模型对EMI滤波抑制的定量评估效果，后续将研究IGBT寄生电容、屏蔽电缆类型、电缆长度、电机绕组对地电容等屏蔽接地措施对系统电磁干扰的影响，以进一步通过仿真模型来指导系统的电磁兼容正向设计。