中国工业企业数据库（1999~2013）的使用研究：基于插值处理方法的比较分析

张少华 李苏苏

摘 要：中国工业企业数据库已经成为研究中国微观企业活动的首选数据库，但是数据库中关键指标的缺失严重影响了数据库的更新和使用。本文在借鉴主要文献处理方法的基础上，先后采用单值移动时序平滑法、MICE1、MICE2、MMICE1和MMICE2五种插补方法对数据库进行完善，从而将中国工业企业数据库延伸至2013年，并通过计算企业全要素生产率来评估各种插补方法的相对有效性。研究表明：在這五种插值方法中，单值移动时序平滑法和MMICE1是两种最为有效的插值方法，不仅可以实现插值前后的数据库特征一致，而且能够实现所计算的全要素生产率的数据结构特征一致。值得强调的是，在完善数据库和计算全要素生产率方面，前者因为处理过程简单因而是一种相对经济的方法，而后者因为能够保留更多样本信息因而是一种相对有效的方法。本文研究价值体现在对使用中国工业企业数据库提供了基础性研究工作。

关键词：中国工业企业数据库;单值移动时序平滑法;多重链式方程插补法;混合插补法;全要素生产率

文章编号：2095-5960（2021）05-0020-10;中图分类号：F011;F016;F42

;文献标识码：A

一、引言

目前，中国工业企业数据库已经成为研究中国经济问题的一个非常重要的微观数据库，因其来源权威、统计规范、样本巨大以及指标多样等优良特性而得到了海内外学者的广泛使用和认可。其研究成果不仅发表在《经济研究》《管理世界》《中国工业经济》《数量经济技术经济研究》等国内权威期刊，也大量出现在《美国经济评论》《政治经济学期刊》《经济学季刊》《金融研究》等国际顶级期刊。但是令人遗憾的是，目前学者们使用的中国工业企业数据库样本主要局限在1999年至2007年，尽管主要研究机构已经将数据库更新至2013年，但是由于2008年之后的多个关键指标缺失问题，导致数据库无法更新到2013年。因此，如何采用科学方法将数据库进行完善和更新，是一项基础性研究工作。

关于中国工业企业数据库的使用问题，事实上国内外学者已经进行了大量深入研究和探讨。例如，Brandt et al.最早规范使用该数据库，其在面板构建、行业调整、价格平减等方面的处理一直被后续学者采用。[1]而国内学者聂辉华等在Brandt et al.基础上，明确指出数据库存在的样本匹配混乱、变量大小异常、测量误差严重以及指标缺失等问题[2]，并首次提出采用交叉匹配法来构建面板。张天华和张少华则运用1998～2007年的中国工业企业数据库讨论了生产函数模型、样本范围和价格因子在不同估计方法中对企业全要素生产率估计的影响。[3]在近期数据的使用上，陈林对数据库的真实性和系统性误差进行了定量评估，并指出样本范围及统计口径的变动，缺失值较多、“回避规模以上”以及“化整为零”等方面的数据问题，均会对数据规范使用产生一定的影响。[4]随后其更进一步从中国工业统计的理论体系和制度变迁角度，探讨了相对频繁的统计制度变迁对样本统计范围和统计口径产生的系统性误差影响。[5]

本文在系统梳理使用中国工业企业数据库的文献后发现，1999～2007年区间的数据处理方式已逐渐形成共识，尤其体现在面板构建、行业调整、价格平减以及样本筛选等方面，正是因为2008年后数据库关键指标的严重缺失，从而使得该数据库的使用在时序上无法推进。为此，本文主要研究目标就是解决中国工业企业数据库的关键指标缺失问题。在遵循文献主要处理方法基础上，先后采用五种插补方法：单值移动时序平滑法、多重链式方程插补法1（MICE1）、多重链式方程插补法2（MICE2）、混合插补法1（MMICE1）和混合插补法2（MMICE2），对中国工业企业数据库进行更新和完善，并进一步通过计算全要素生产率这个使用数据库最为频繁的指标，实证评估各种插补方法的相对有效性。

二、插值处理方法

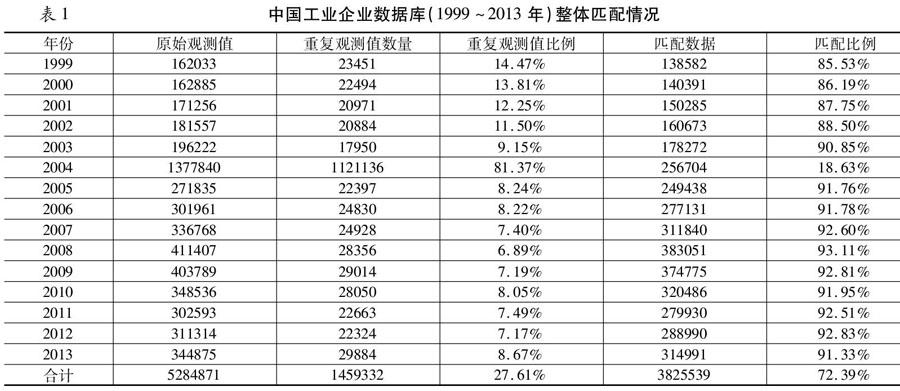
下文详细介绍对中国工业企业数据库中的缺失指标如何采用五种插补方法进行指标插补。事实上，对于中国工业企业数据库的处理，还需要进行面板构建、行业调整、价格平减、派生指标计算、样本筛选等一系列的处理过程，本文在此处不进行详细的介绍，这些处理过程可以参考李苏苏、叶祥松和张少华，以及李苏苏、张少华和周鹏[6，7]。在进行插值处理之前，首先需要进行面板数据构建，本文改进了现有文献的交叉识别方法，遵循尽量在数据库中识别同一企业原则，采用三个步骤进行匹配，具体匹配效果见表1。

表1中的重复观测值包括通常意义上的重复观测值和上面所提到的同一年份同一企业ID有多个观测值且法人代码相同的情况;重复观测值的比例指重复观测值占原始观测值总数的比例，匹配数据是指构建面板后删除重复观测值后剩下的年度观测值总数;匹配比例指匹配数据占原始观测值总数的比例。其中2004年数据融合了中国经济普查企业数据，故原始观测值总数较多，匹配率相对较低。由于2010年数据异常，本文不予使用，在构建面板的时候没有删除，是为了在匹配的时候保留更多的企业信息。构建面板后本文借鉴王万珺和刘小玄的做法，去掉2010年数据将2009年和2011年视为连续年份处理，原始数据观测值总数为4936335，删除重复值之后，匹配数据数量为3505053。[8]如果不考虑2004年数据融合的影响，数据库总体匹配比例高达85%以上，而且匹配比例逐年提高，说明匹配效果稳步提升。

（一）插值前的准备

中国工业企业数据库自2008年始，数据库中诸多关键指标缺失，这里将根据五种方法对数据库缺漏值进行插补，每一种插补方法后文详细说明。本文对缺失指标按照“先计算，后插补”的原则进行处理，并且以全要素生产率的估算为例进行详细阐述。

1.先计算

具体过程如下：对2004年缺失的工业总产值与工业增加值，在使用2004年中国经济普查企业数据进行融合后还缺少工业增加值指标，通过“工业增加值=工业总产值-工业中间投入+增值税”计算得出。关于本年折旧，对2007年前本年折旧缺失的样本以及2008～2009年的数据进行补全处理，若上一年存在固定资产总值，采用“固定资产投资=当年固定资产总值-（1-折旧率）×上年固定资产总值”来补充计算，折旧率折中取10%。[2，9]这样可以利用固定资产投资推算2008～2009年的本年折旧。

关于缺失的2008～2013年的工业中间投入和工业增加值，借鉴余淼杰等的方法，采用“工业中间投入=产出值×销售成本/销售收入-工资支付-本年折旧”和“工业增加值=工业总产值+增值税-工业中间投入”先后得出。[10]由于2009年工资支付缺失，这样，在计算企业全要素生产率指标中，还缺失2009年的工业中间投入和工业增加值，需要通过插值方法来获得。

2.离群值、异常值缺漏化处理

為保留尽可能多的观测值，在插值前本文对异常值做如下处理：①通过画指标的核密度函数图，将工业增加值a17、固定资产合计a25、工业中间投入a70左右端十万分之一的离群值设为缺漏值。②将关键指标如工业总产值、从业人员年平均人数、固定资产合计、职工人数缺失或者小于等于0的观测值设为缺漏值。③对于所用到的明显不符合会计原则的观测值，如“资产总计<固定资产合计”“工业增加值>工业总产值”“工业中间投入>工业总产值”的观测值，保留理论上相对较大的指标值，将对应的固定资产合计、工业增加值、工业中间投入设为缺漏值。

经过如上处理，总样本和工业增加值、工业中间投入和本年折旧的观测样本发生了一系列变化，具体如表2所示。从表2最后一列的缺失率计算结果来看，需要插值处理的工业增加值a17、本年折旧a28、工业中间投入a70指标的缺失率分别由46.93%、23%、46.84%降低为15.98%、5.42%、16.25%。很大程度上对数据库进行了完善，也为接下来插值处理与效果评估提供了基础。

（二）五种插补方法

经过一系列数据分析与处理，可以观察到要计算全要素生产率关键在于对2008～2009年本年折旧和2009年工业中间投入和工业增加值缺失值的处理。关于本年折旧缺失值的处理，王万珺和刘小玄提到采用固定资产和两位数行业信息，利用单值插补和多元线性回归重复插值十次，以第十次的插值替代缺失值。[8]究竟这种多重插补在大样本数据中是否合适？是否较单值插补法更为优越？通过不断的尝试，本文最终采用单一插补中的单值移动时序平滑法、和多重插补中的链式方程法以及这两者的混合插补对数据库进行处理，并比较它们的效果。具体介绍如下：

单值插补（移动平滑插补）：原始数据 公式计算1 移动平滑插值 公式计算2 插值结果1

多重插补（MICE1）：原始数据 公式计算1 分省份分行业多重插值MICE 插值结果2

多重插补（MICE2）：原始数据 公式计算1 分省份多重插值MICEI 插值结果3

混合插补（MMICE1）：原始数据 公式计算1 移动平滑插值 分省份分行业多重插值MICH 插值结果4

混合插补（MMICE2）：原始数据 公式计算1 移动平滑插值 分省份多重插值MICEH 插值结果5

1.单值移动时序平滑插补

单一插补（Single Imputation）就是给一个缺失单元（变量）补上一个合理的值。本文通过移动时序平滑插值法来获得2009年工资支付，进而利用“工业中间投入=产出值×销售成本/销售收入-工资支付-本年折旧”和“工业增加值=工业总产值+增值税-工业中间投入”计算出缺失的工业中间投入和工业增加值。

然后再对于数据库中存在缺漏的主要变量使用单值移动时序平滑插补法进行均值插补处理。在插补的基础上再通过上面公式计算出部分缺漏的本年折旧、工业中间投入与工业增加值。经过如上两轮的计算和插补后，将工业总产值a14还存在缺失的观测值进行删除处理，其原因在于a14作为多数研究的核心指标，从数据库本身的情况来看a14缺失的观测变量相应地其他指标也缺失严重，这样的观测值并不能为研究提供更多的信息。最终得到数据结果如表3所示。

2.多重插补

根据经验，如果大样本数据某个或某些变量的缺失比例超过5%，则可能需要进行多重插补。多重插补（multiple imputation）是给每个缺失单元（变量）插补上多个值，并将这些值合并为一个综合的结果，进而运用这个被综合处理的数据集对变量进行描述或者研究变量之间的关系。多重插补以完全随机缺失、随机缺失机制为前提，要求尽可能保证数据缺失与观测来的数据有关，与未观测到的数据无关。如果说单一插补的假定是从回答数据中能够预测出缺失数据的“最佳值”，那么多重插补则的假定是从回答数据中能够找出缺失数据的概率分布。

本文运用了MICE（Multivariate Imputation by Chained Equations）链式方程法对缺漏值进行插值处理。在进行MICE 插值前，我们对参考指标和插值指标进行了共线性测度，对VIF值超过10的参考指标如工业销售总产值a14b、流动资产合计a18、资产总计a31、所有者权益合计a36、主营业务收入a39、主营业务成本a40等进行剔除。在进行MICE插值时，我们作了两种处理以作对比，第一种为同时控制行业与地区，将数据集分为30×31个子数据集来进行处理，在文中我们记为MICE1。第二种为控制地区的同时将行业设为哑变量，将数据集分为31个子数据集来进行插值处理，记为MICE2。在插补时，对于使用同类回归方法的变量可以排列在一起，程序在执行插补的时候会自动按照缺失值从低到高的顺序依次执行。我们分别运用这两种方法对数据库中主要的关键变量进行10次插补取平均值。插补观测值的变化情况归纳为表5所示。由于链式方程法与单值移动时序平滑法的插值原则不同，在链式方程法前需对参考变量中存在缺失值的观测值作删除处理，因此得出采用MICE1和MICE2进行插值前的观测值数量分别为3，293，169和3，381，821。由表4可见，经MICE1和MICE2多重插补以后，缺失值相较于插值前的观测值数量得到完全的填充。

3.混合插补

考虑到单纯进行单值移动时序平滑插值以后还存在较多的缺失值，而单纯的多重插值因数据量过于庞大不可能对单个个体进行控制使得插值效果不尽人意，经不断实践，本文发现在进行单值移动时序平滑法插值后，再进行如上相应的多重插补能够获得很好的效果，且各自变量的相对效率均高于98.6%，在单纯的多重插补92.8%的基础上提高不少。我们将相应的插补方式记为MMICE1和MMICE2。在单值移动时序平滑法的插值之后链式方程法插值之前需对参考变量中存在缺失值的作删除处理，因此得出MMICE1和MMICE2插值前的观测值数量为3，381，791和3，382，121，具体如表5所示。可见，经MMICE1和MMICE2多重插补以后，缺失值相较于插值前的观测值数量得到完全的填充。

（三）五种插值方法效果比较

在完成插值以后，需要对插值效果进行检验。首先，我们从感性的角度上来考察它们分别对数据库的补充程度，即比较它们的插值后数据库的完善情况，本文将结果归纳如表6所示。可见，在对数据库的完善程度来看，原始观测值为3，505，053，单值插补的插值后存在值占原始观测值的比例为63.95%～94.42%，多重插补MICE1、MICE2的比例分别达到93.95%和96.48%，混合插补因其结合了单值插补和多重插补的优点，MMICE1、MMICE2的比例分别达到96.48%和96.49%。从对数据库指标完善的程度上来看，混合插补具有相对优势。

上面我们对插值后观测值统计量变化情况进行了比较。因在插值前我们对异常值进行了缺漏设定，现在具体考察插值后异常值的统计情况，如表7所示。从中可以看出，采用MMICE1方案所得到的正常样本的比例最高（94.45%），其次是MICE1（93.49%），然后是MICE2（91.83%）和MMICE2（91.16%），最后是移动平滑插补（83.68%）。移动平滑插补所得到的正常样本比例最低，主要源于它对缺漏值所做的插补有限，在计算后的数据基础上只增加了4528个观测样本。同样地，我们可以衡量其他四种插值方法的插值效果，其中MMICE1在计算后的数据基础上增加了123262个观测样本且正常样本达到94.45%。從这个意义上来说，MMICE1的插值效果具有相对优势。

上面两种方式主要是从对数据完整程度的改善和插补后异常值/正常值的对比情况来反应插值的效果，并不能准确判别出哪种方式更好。具体哪种插补方法能被应用于实证研究，关键还在于插值前后具体指标数据的结构是否改变。如何考察这样庞大的数据集指标结构的变化，我们尝试考察插值前后的指标分布结构是否有较大差异，具体参见表8。

根据已有文献的做法，我们以MICE1和MICE2多重插补下的估计结果作为参考基准。发现个案删除（表中原始列）、移动时序平滑插值法的估计都是有偏的，只有混合插补MMICE1和MMICE2的插补结果较为接近多重插补下的估计结果，与多重插补相比，删除个案、移动时序平滑插补方法在多数样本上均显示出低估了样本的标准差。

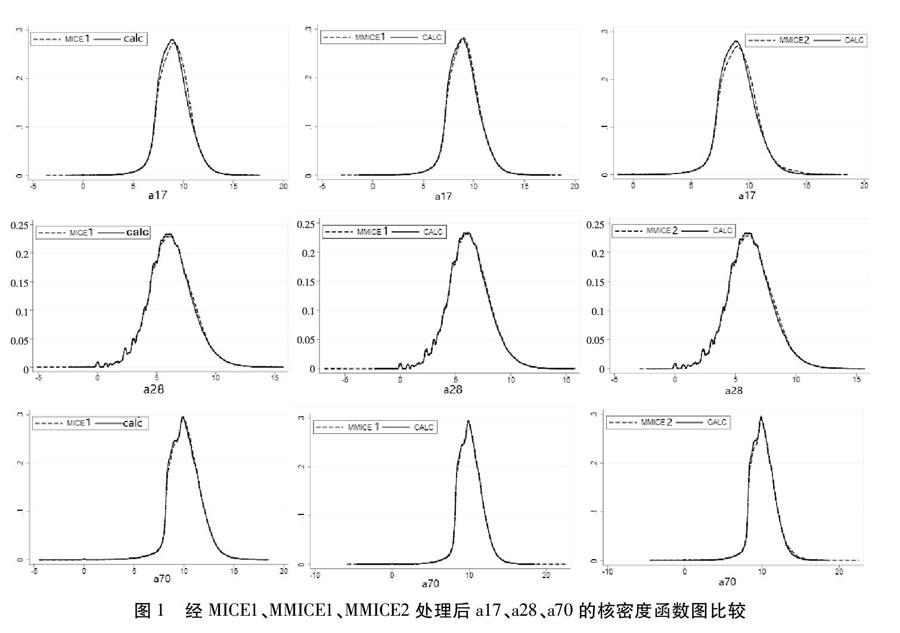
具体多重插补和混合插补哪一种更适合我们后续的实证研究，我们还将多重插补MICE1及混合插补MMICE1、MMICE2插值前后的a17、a28、a70对数的核密度函数图与原始数据计算补充后相应指标的核密度函数图进行拟合，发现虽然拟合程度都很高，但MMICE1基本上能与原始数据所得出的核密度函数图相重合，如图1所示。在插补过程的检验中自变量的相对效率也体现出混合插补相对于多重插补的优越性。因此，我们认为MMICE1的插值结果最有效合理。遂将MMICE1插值后的数据库用于下文企业全要素生产率的测度。

三、插值效果评估

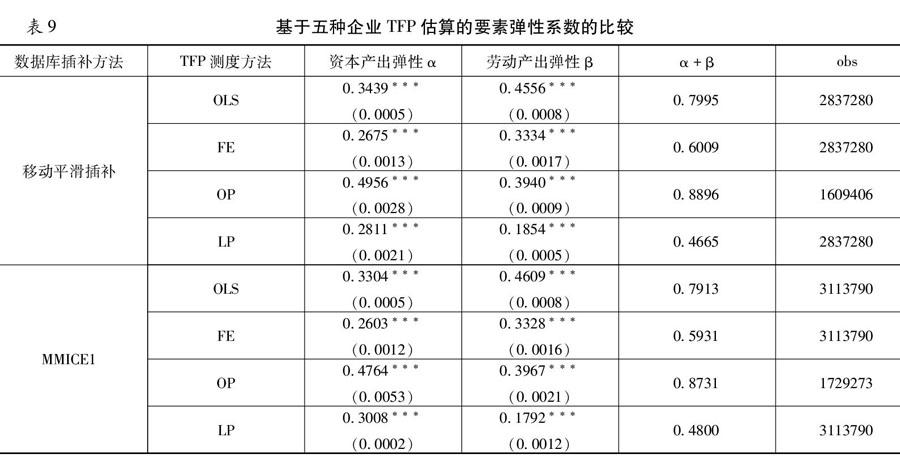
鉴于全要素生产率的测度是使用中国工业企业数据库进行的最为广泛的一个研究领域，本文在上述两种相对最有效的插补方法建立的数据库基础上，分别采用OLS、FE、OP方法、LP方法来计算中国工业企业的TFP，以进一步评估不同插补方法的效果。表9是基于单值移动平滑和MMICE1插补后采用如上四种方法估计的结果。研究表明，采用OLS回归与FE方法计算的劳动产出弹性系数高于资本产出弹性系数，采用OP方法和LP方法计算的资本产出弹性系数则高于劳动产出弹性系数。根据现有研究可知，OLS回归与FE 方法计算TFP会产生联立性偏误和样本选择性偏误这两种重要问题，因此会导致劳动产出弹性系数被高估。与此同时，我们发现OP 方法计算的资本产出弹性系数和劳动产出弹性系数均显著高于LP方法计算结果。

表10是基于两种主要插补方法建立数据库基础上，进而采用四种TFP计算方法对中国工业企业的全要素生产率进行重新测度，最后得出表中的描述性统计数据，并且分别画出了四种TFP估计方法估计结果的核密度分布函数图，如图2所示。从表10以及图2可以看出，基于两种插值方法建立的数据库无

论是在计算TFP的资本和劳动弹性系数上，还是在计算TFP的数据分布特征上，两种插值方法呈现出来的差异都非常小，这一方面验证了我们数据处理过程的合理性，另一方面说明了两种插补方法的相对有效性。值得强调的是，尽管这两种插补方法建立的数据库在计算TFP的效果上的差异较小（这说明这两种方法建立的数据库都能够捕捉到TFP的基本分布特征信息），但是由于混合插补法的MMICE1能够在保证计算指标有效性的同时保留更大的数据样本，进而保留更多的关键数据信息。因此，本文认为相对于移动平滑法，混合插补法MMICE1在数据库完善和关键指标获取方面更为有效。同时，考虑到移动平滑法是一种最为简单的插补方法，即使没有过多的技术处理仍然可以取得相当完美的计算结果，因为本文认为移动平滑法是一种更加经济有效的插补方法。

参考文献：

[1]Brandt Loren，Biesebroeck Johannes Van， and Zhang Yifan. Creative accounting or creativedestruction？ Firm-level productivity growth in China[J]. Journal of DevelopmentEconomics， 2012， 97：339～351.

[2]聂辉华，江艇，杨汝岱.中国工业企业数据库的使用现状和潜在问题[J].世界经济，2012（5）.

[3]张天华，张少华.中国工业企业全要素生产率的稳健估计[J].世界经济，2016（4）.

[4]陈林.中国工业企业数据库的使用问题再探[J].经济评论，2018（6）.

[5]陈林.中国工业统计的理论体系和制度变迁：兼议中国工业企业数据的部分系统性误差[J].经济科学，2019（4）.

[6]李苏苏，叶祥松，张少华.中国制造业企业全要素生产率测度研究[J].学术研究，2020（3）.

[7]李苏苏，张少华，周鹏.中国企业出口生产率优势的识别与分解研究[J].数量经济技术经济研究，2020（2）.

[8]王万珺，刘小玄.为什么僵尸企业能够长期生存[J].中国工业经济，2018（10）.

[9]苏锦红，兰宜生，夏怡然.异质性企业全要素生产率与要素配置效率——基于1999～2007年中国制造业企业微观数据的实证分析[J].世界经济研究，2015（11）.

[10]余淼杰，金洋，张睿.工业企业产能利用率衡量与生产率估算[J].经济研究，2018（5）.

Research on the use of China industrial enterprise database （1999～2013）：

Comparative analysis of missing value processing methods

ZHANG Shao-hua，LI Su-su

（Guangzhou University，Guangzhou，Guangdong 510006，China;Guangdong University of Finance and Economics，Guangzhou，Guangdong 510320，China）

Abstract：

China industrial enterprise database has become the preferred database to study China's micro enterprise activities. However， the lack of key indicators in the database seriously affects the update and use of the database. On the basis of referring to the main literature processing methods， this paper uses five interpolation methods to improve the database， including single imputation， MICE1、MICE2、MMICE1和MMICE2， so as to extend the Chinese industrial enterprise database to 2013， and evaluate the relative effectiveness of various interpolation methods by calculating the total enterprise productivity. The results show that： In the five interpolation methods， the single imputation method and MMICE1 are the two most effective interpolation methods， which can not only achieve the consistency of database features before and after interpolation， but also achieve the consistency of data structure features of total factor productivity. It is worth emphasizing that in terms of improving the database and calculating the total factor productivity， the former is a relatively economic method because of its simple process， while the latter is a relatively effective method because it can retain more sample information The research value of this paper is to provide basic research work for the use of Chinese industrial enterprise database.

Key words：

chinese industrial enterprise database;single imputation;multivariate imputation by chained equations;mixed interpolation method;total factor productivity

責任编辑：吴锦丹

收稿日期：2021-03-05

基金项目：国家社会科学基金重大攻关项目“全面建成小康社会背景下新型城乡关系研究”（17ZDA067）;国家自然科学基金常规面上项目“中国的“中部迷失”问题：典型事实、形成机理及宏观后果”（批准号：71673253）、“中国企业和城市规模分布异化的政策根源、形成机制与效率评估”（批准号：72073038），以及广州市宣传文化人才培养专项经费资助的成果之一。

作者简介：张少华（1975—），男，山西阳城人，广州大学经济与统计学院教授、博导，中山大学博士，浙江大学博士后，研究方向为资源错配与全要素生产率研究;李苏苏（1984—）（通讯作者），女，湖南娄底人，广东财经大学讲师，博士，研究方向为生产率测度与分解研究。