基于启发式矩匹配法的分布式电源选址定容方法

郑 建，徐青山，施雨松

（东南大学电气工程学院，南京 210096）

分布式电源具有清洁、环保、成本低等优点[1]。在配电网中适当安装分布式电源可以提高电能质量、降低网损、减小峰谷差以及提高供电可靠性[2-3]。然而，由于风电和光伏等分布式可再生能源输出的随机性和间歇性，可能对配电网产生不利影响，如电压波动等，从而影响配电网的经济性和可靠性[4-5]。

分布式电源规划一般包括选址和定容两项任务。根据不同的规划目标，获得最优的分布式电源安装位置和容量[6]。目前主流的规划方法可以分为两类：经典方法和人工智能方法[7]。随着配电网规模的增大，经典方法的求解比较耗时且收敛速度慢[8]。为了解决这一问题，基于人工智能的算法在分布式电源规划中得到了广泛应用[9]。

可再生分布式能源输出的间歇性、随机性以及负荷需求的波动性，是分布式电源规划中不容忽视的问题[10]。为了确保分布式电源规划的有效性，必须对这些不确定性进行建模。分布式电源优化规划问题中处理不确定性的方法包括随机规划[11]、鲁棒优化[12-13]和元启发式算法。文献[14]将蒙特卡罗模拟法与弯曲分解算法相结合，探讨了系统扩展规划中风电功率和负荷需求的不确定性；文献[15]采用蒙特卡罗模拟法对风电场的盈利能力进行了分析。然而，为了精确地近似不确定性，在使用蒙特卡罗方法时需要大量的场景，这将导致计算负担沉重[16]。与蒙特卡罗模拟法相比，启发式矩匹配HMM（heuristic moment matching）法的代表性场景更少，从而减少了计算量[17]。

随着配电网规模的增大，若在选址时将配电网中的所有节点都作为候选节点，将极大地增加计算负担，使规划效率大大降低。为了提高规划效率，有必要对配电网中的节点进行优选，确定若干合适的候选节点。已经有学者提出一些方法来分析配电网的节点对系统波动的敏感性。文献[18]提出一种电压稳定指数VSI（voltage stability index）模型，从电压稳定的角度分析系统中的敏感节点作为接入分布式电源候选节点；文献[19]采用损耗灵敏度因子法LSFs（loss sensitivity factors），从网络损耗的角度分析系统中的敏感节点，从而大大减小了候选节点的范围。采用不同的指标来分析节点的敏感性，可能会导致在分析过程中产生冲突，综合加权法可以有效地避免此类问题。

本文首先采用综合多种灵敏度指标的方法确定分布式电源安装候选节点的顺序，以减小潜在求解空间的范围。然后采用启发式矩匹配法分析不确定性，通过捕获历史场景的目标矩（包括期望、方差、偏度和峰度）和相关性，得到风速、辐照、环境温度和负荷需求的代表性场景。最后基于生成的代表性场景，以年综合费用最小和平均电压偏差最小为目标，采用非支配排序遗传算法NSGA-Ⅱ（non-dominated sorted genetic algorithm-Ⅱ）进行优化求解，确定最佳的分布式电源接入位置和容量。以IEEE-33 节点配电系统为例，验证了本文所提模型的有效性。

1 基于灵敏度指标确定候选节点

本文采用综合多种灵敏度指标的方法确定分布式电源安装候选节点顺序。如图1 所示是一端为源、一端为负载、两端为2 个节点的简单径向配电系统的等效电路。

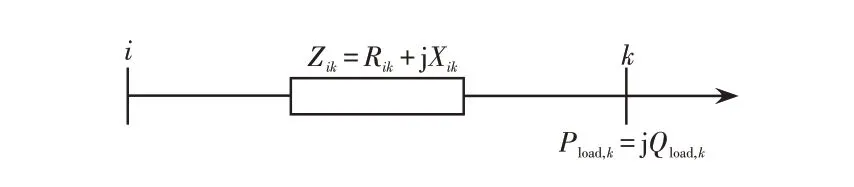
图1 径向配电系统的等效电路Fig.1 Equivalent circuit of radial distribution system

1.1 电压稳定指数

电压稳定指数模型从电压稳定的角度分析系统中的脆弱节点。电压稳定指数VSI 越接近于1，系统越不稳定。VSI 高的节点更敏感，可用于分布式电源的优化部署。电压稳定指数的数学模型[18]描述为

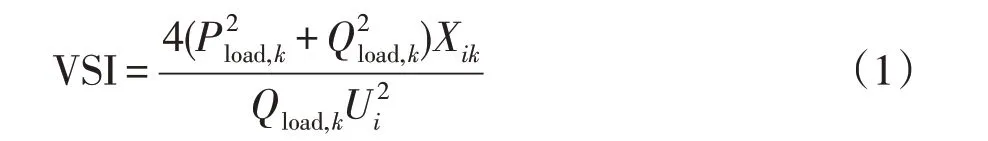
式中：Pload,k和Qload,k分别为节点k的有功负荷和无功负荷；Xik为支路i-k的电抗；Ui为节点i的电压。

1.2 损耗灵敏度因子

损耗灵敏度因子法从网络损耗的角度分析系统中的敏感节点，损耗灵敏度因子高的节点可以考虑接入分布式电源。损耗灵敏度因子的计算公式[19]为

式中：LSFs 为损耗灵敏度因子；PL,ik为支路i-k的有功损耗；Rik为支路i-k的电阻；Uk为节点k的电压。

1.3 归一化指标

求出电压稳定指数和损耗灵敏度因子指标后，可进行归一化处理为

式中：D(j)和DN(j)分别为指标D的第j个值及其归一化值；Dmax和Dmin分别为指标D的最大值和最小值。

1.4 综合指标

不同节点灵敏度指标从不同角度考虑配电网的运行特性。采用不同指标分析节点的敏感性，可能会导致分析过程中产生冲突，综合加权法可以有效地避免此类问题。其综合指标的计算公式为

2 不确定性建模

2.1 场景矩阵

本文采用启发式矩匹配法得到风速、辐照、环境温度和负荷需求的代表性场景。

图2是由H个风速、辐照、环境温度和负荷需求的代表性场景组成的场景矩阵示意，其中，这些代表性场景的范围均在历史数据的上限和下限之间。

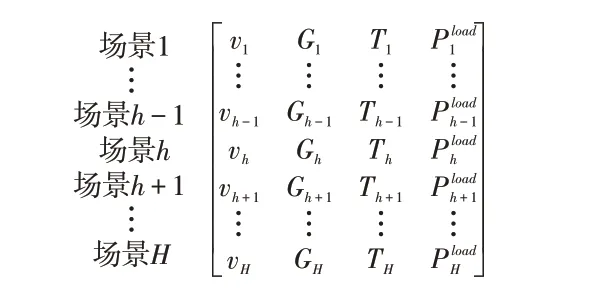
图2 场景矩阵示意Fig.2 Schematic of scenario matrix

2.2 HMM 法生成代表性场景

采用HMM法生成代表性场景的步骤如下。

步骤1 计算历史风速、辐照、环境温度和负荷需求数据的前4阶中心距，生成目标矩阵Mi,k(i=1,2,3,4),分别对应风速、辐照、环境温度和负荷需求；k为阶数,k=1,2,3,4。

步骤2 为了便于计算，对目标矩阵Mi,k进行标准化。标准化公式为

式中：rij为向量Ai和向量Aj之间的相关系数；Cov(Ai,Aj) 为向量Ai和向量Aj之间的协方差；Var(Ai)和Var(Aj)分别为向量Ai和向量Aj的方差。

步骤4 生成服从N（0，1）正态分布的4×NH维随机矩阵X（NH为生成的场景数），X由4个独立行向量Xi（i=1,2,3,4）构成。

步骤5 矩阵变换。采用Cholesky分解得到相关矩阵R的下三角矩阵L，并计算目标相关矩阵Y，计算公式为

2.3 分布式电源输出功率建模

2.3.1 风机输出功率模型

风机的出力和风速之间的关系[20]可近似表示为

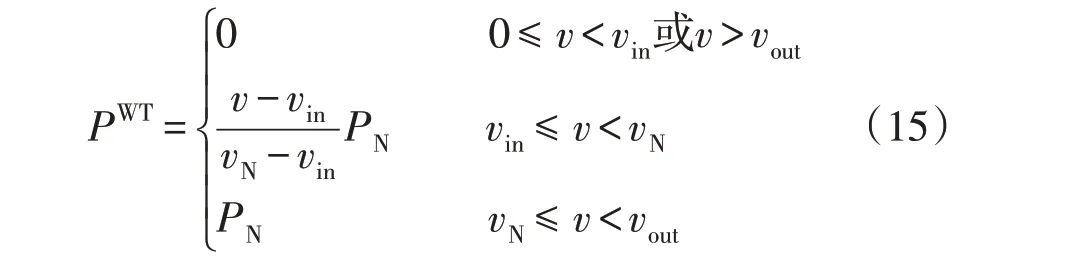
式中：PWT和PN分别为风机的实际输出功率和额定功率；vin、vN和vout分别为切入风速、额定风速和切出风速。

2.3.2 光伏系统输出功率模型

光伏系统输出功率受天气等自然条件影响，影响因素包括太阳辐射强度、温度等。光伏系统的输出功率[21]的计算公式为

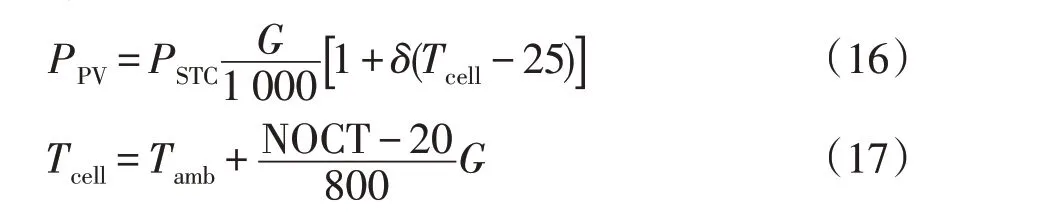
式中：PPV和PSTC分别为光伏系统的实际输出功率和额定功率；G为当前情况的太阳辐射强度；δ为功率温度系数；Tcell为电池组件温度；Tamb为环境温度；NOCT 为国家电池工作温度。

3 含分布式电源配电网优化规划模型

3.1 目标函数

本文以年综合费用最小和平均电压偏差最小为目标，确定风机和光伏系统的最佳接入位置和容量。

3.1.1 年综合费用最小

目标函数1 为最小化年综合费用，其数学表达式为

式（18）中各参数的含义和计算公式分述如下。

（1）折算到每年的风机和光伏系统的固定投资费Cin，计算公式为

式中：a为上级电网单位发电量所排放的碳；cc为碳排放单价。

3.1.2 平均电压偏差最小

目标函数2 为最小化平均电压偏差，其数学表达式为

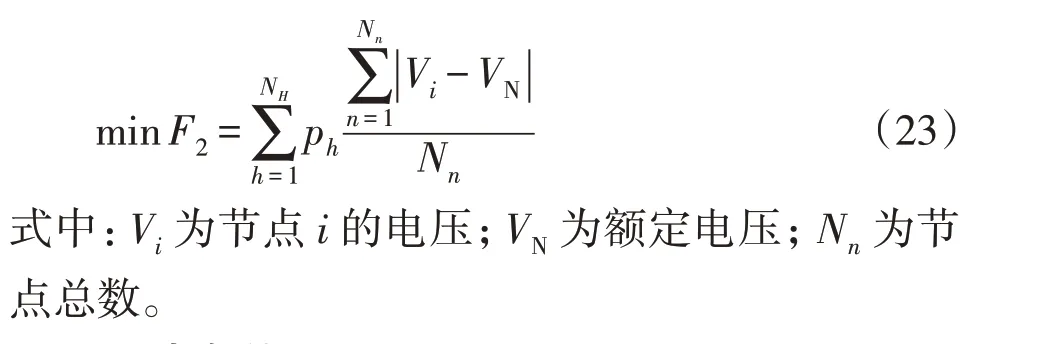
3.2 约束条件

（1）潮流方程约束为

式中：Pi和Qi分别为节点i的有功功率和无功功率；Vj为节点j的节点电压；Bij、Gij和δij分别为节点i和j之间的电导、电纳和电压相角。

（2）线路功率约束为

式中：ρ为穿透功率系数；Pload,i为节点i的负荷。

（5）节点约束条件为

考虑土地面积约束，节点i最多可以接入MWT个风机和MPV个光伏系统，约束为

式中，λi,WT和λi,PV分别为节点i接入的风机和光伏系统个数。

4 基于NSGA-Ⅱ算法的多目标优化

在多目标优化问题中，多个规划目标一般难以同时达到最优。NSGA-Ⅱ是带精英策略的非支配排序遗传算法，它一种基于Pareto 最优解的多目标优化算法[22]，已经被成功应用于多个实际工程。本文采用NSGA-Ⅱ算法来求解提出的多目标优化问题。

4.1 优化规划流程

在优化规划过程中，接入风机和光伏系统的容量和位置均对年综合费用和平均电压偏差产生不同影响。为了提高遗传算法的搜索能力，本文对染色体进行分段式编码、交叉和变异。染色体编码如图3所示。

图3 染色体编码Fig.3 Chromosome coding

图3 中“风机位置”和“光伏系统位置”子段采用二进制编码，Li为1表示该节点被选择接入分布式电源，Li为0 则表示该节点不接入分布式电源。“风机容量”和“光伏容量”子段采用整数编码，Ci为该节点选择接入的分布式电源容量。

基于NSGA-Ⅱ算法的含分布式电源的配电网优化规划流程如图4所示。

图4 优化规划流程Fig.4 Flow chart of optimization planning

4.2 确定最佳折中解

实际工程中最终的解决方案往往只有一个，因此需要从一组Pareto 最优解中选出一个最佳的折中解。本文采用模糊集理论来确定最优折中解，将Pareto解中各目标函数对应的满意度用模糊隶属度函数表示[23-24]为

5 算例分析

为了验证本文所提含分布式电源配电网的优化规划模型的性能，以IEEE-33节点配电网为例，确定最佳的风机和光伏系统接入位置和容量。基准电压与基准容量分别设为12.66 kV 与1 000 kV·A。IEEE-33节点系统接线图如图5所示。

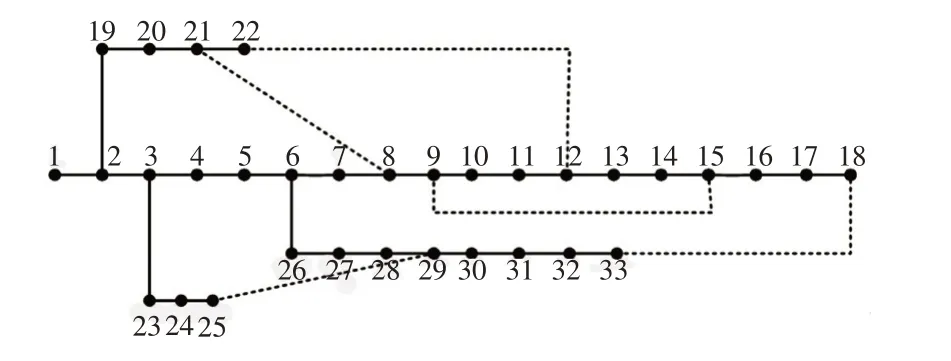
图5 IEEE-33 节点系统接线图Fig.5 Wiring diagram of IEEE 33-bus system

5.1 确定候选节点

在基本情况下进行潮流计算，计算出各节点的电压稳定指数和损耗灵敏度因子，并通过综合加权法计算出节点灵敏度综合指标，结果如图6所示。

本文取节点灵敏度综合指标最高的8 个节点作为候选节点，从图6中可以看出，该8个节点的编号分别为7、17、20、24、25、29、30、31。

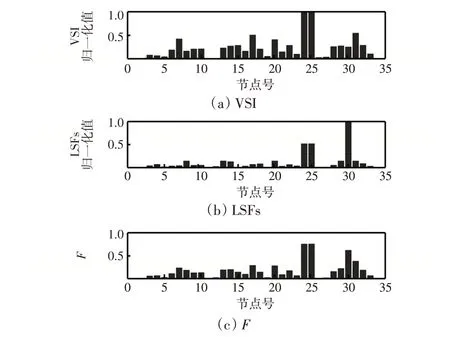
图6 节点灵敏度指标计算结果Fig.6 Calculation results of bus sensitivity index

5.2 代表性场景选择标准

采用启发式矩匹配法获取历史风速、辐照、环境温度和负荷需求的期望、方差、偏度和峰度等统计特性，生成10 个场景矩阵，场景数分别为10～100。计算不同场景数下生成的代表性场景的各阶矩误差，结果如图7所示。

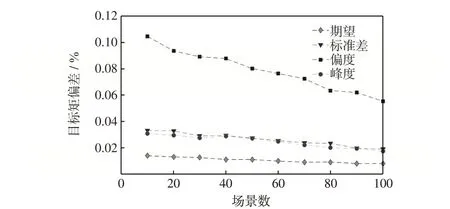
图7 不同场景数下生成场景的矩误差Fig.7 Moment errors of generated scenarios under different scenario numbers

从图7中可见，随着场景数的增加，生成场景的各阶矩误差逐渐减小，说明不确定性矩阵准确地捕捉了风力、光伏发电和负荷的历史数据的随机特征。

然而规划所需的计算时间也会随着场景数的增加而增加，实际规划过程中场景数的选择需要在求解精度和计算效率之间进行最佳权衡。图8 比较了不同场景数下的求解精度和计算效率。

从图8 中可以看出，当场景数达到40 时，随着场景数的增加，年综合费用和电压偏差减小的趋势非常平缓，同时计算时间开始显著上升。因此场景数取为40较合适，生成场景的结果如图9所示。

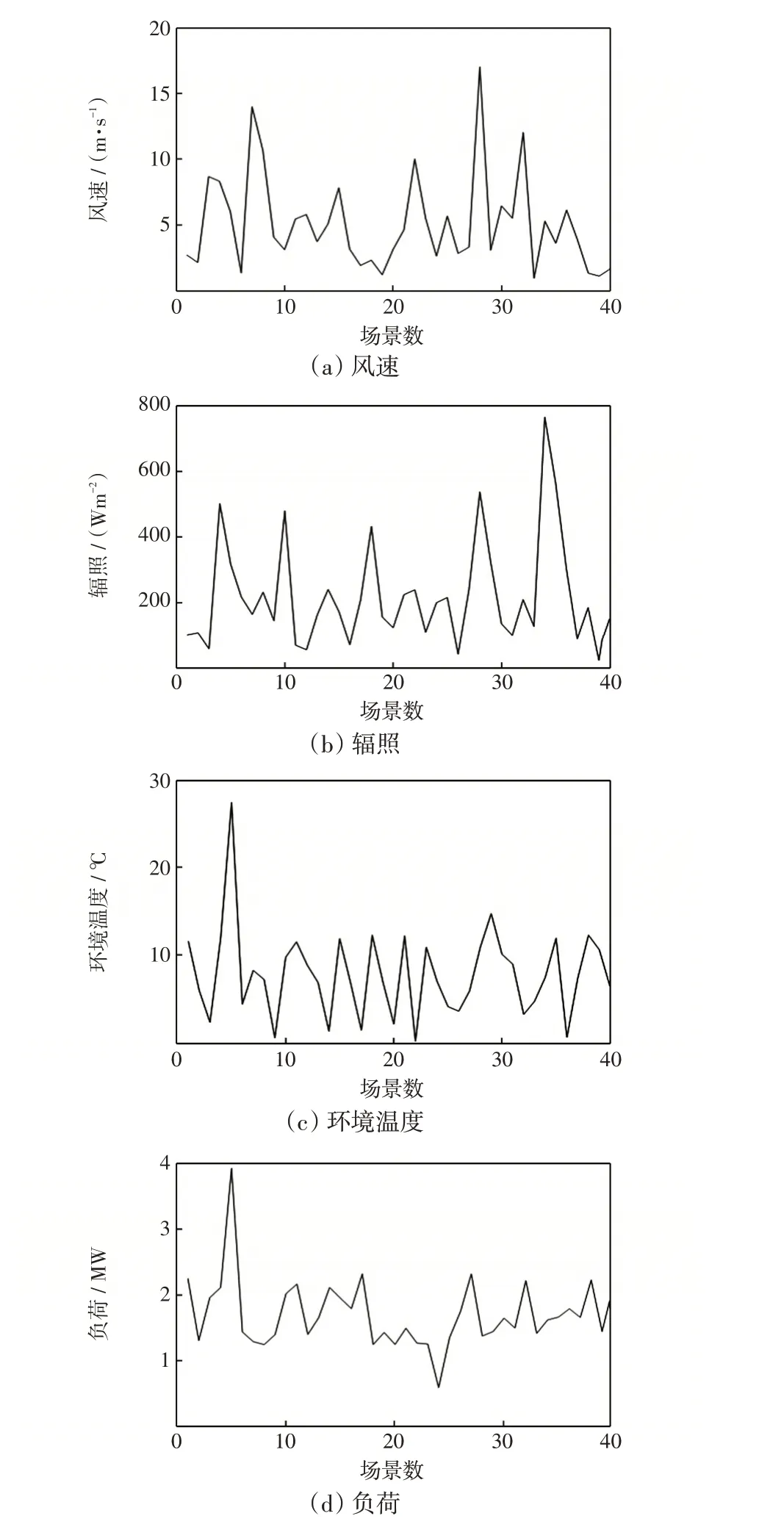
图9 基于启发式矩匹配法生成的代表性场景Fig.9 Representative scenarios generated by heuristic moment matching method

5.3 相关参数和规划结果

根据生成的代表性场景，以年综合费用和平均电压偏差最小为目标，采用NSGA-Ⅱ算法，确定最佳的分布式电源接入位置和容量。相关参数如表1所示。

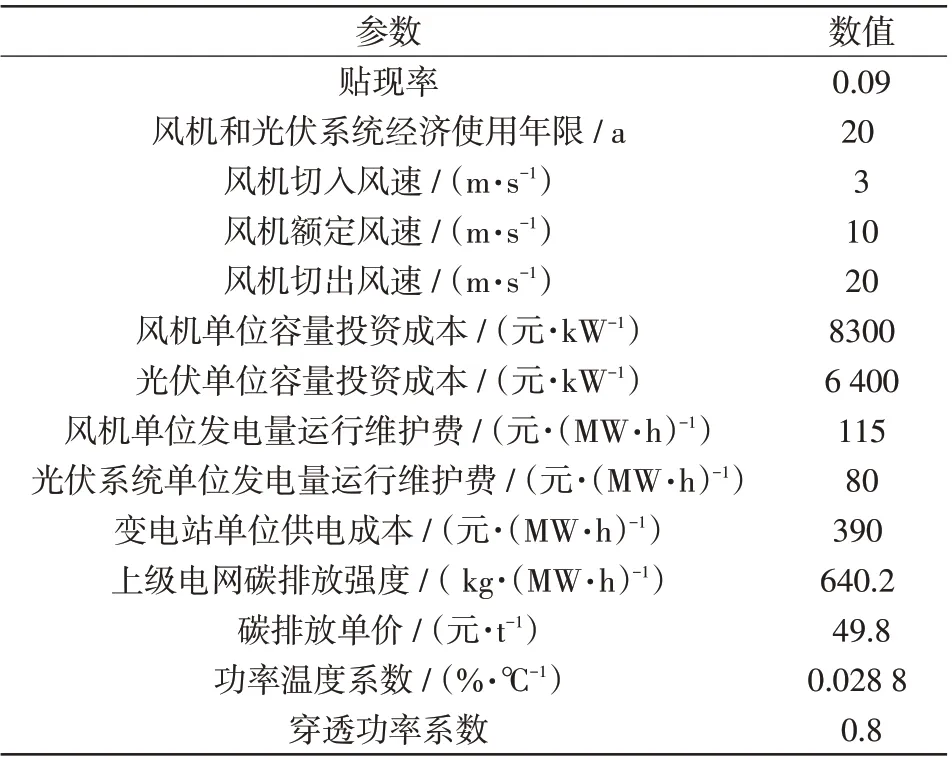
表1 相关参数Tab.1 Related parameters

NSGA-Ⅱ算法的种群规模设为50，迭代次数设为100。得到的Pareto 前沿如图10所示，从图10中可看出，帕累托分布比较广泛，说明帕累托最优集较完整。

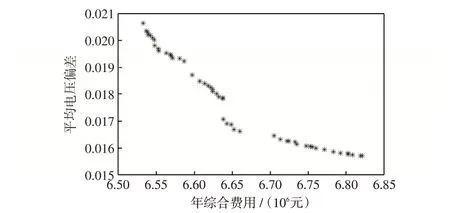
图10 Pareto 解集分布Fig.10 Pareto set distribution

采用模糊集理论来确定最优折中解，结果如图11 所示。从图11 中可以看出，风机最佳接入节点分别为节点17 和节点31，最佳接入容量分别为0.6 MW 和1.0 MW；光伏系统最佳接入节点为节点24，最佳接入容量为0.156 MW。

图11 风机和光伏系统最佳接入位置和容量Fig.11 Optimal access location and capacity of wind turbine and photovoltaic system

接入分布式电源前后相关项目的规划结果如表2 所示。从表2 中可以看出，接入分布式电源后变电站年供电费和环境成本均下降了68.3%；年综合费用下降了54.05%；网络有功损耗下降了56.0%；网络无功损耗下降了54.4%；平均电压偏差下降了67.7%。表2的规划结果表明接入分布式电源后配电网的各项费用都大幅减小，验证了本文所提优化规划模型的有效性。

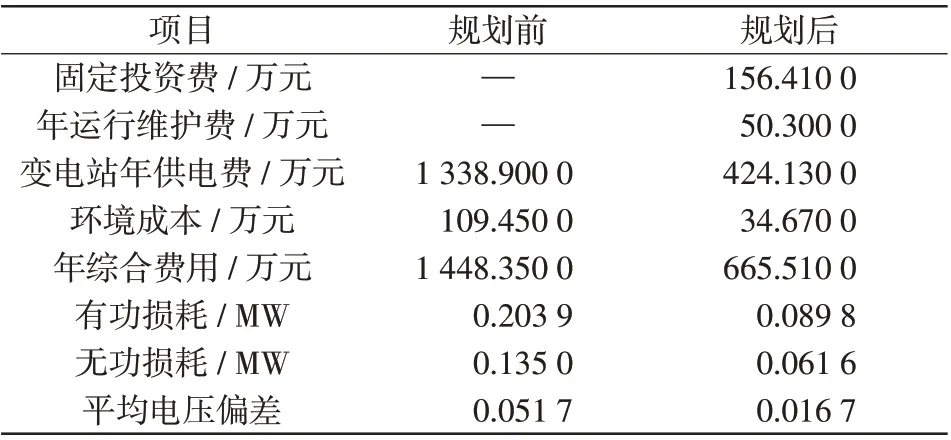
表2 规划结果Tab.2 Planning results

图12和图13分别为接入分布式电源前后配电网的节点电压分布和各支路网损对比。从图中可以看出，接入分布式电源后配电网的电压分布得到了明显改善，各支路的有功网损和无功网损也大幅减小，说明分布式电源接入配电网，提高了系统的整体调控能力，也验证了本文所提优化规划模型的有效性。

图12 接入分布式电源前后配电网的节点电压分布对比Fig.12 Comparison of bus voltage distribution in distribution network before and after the access of distributed generation

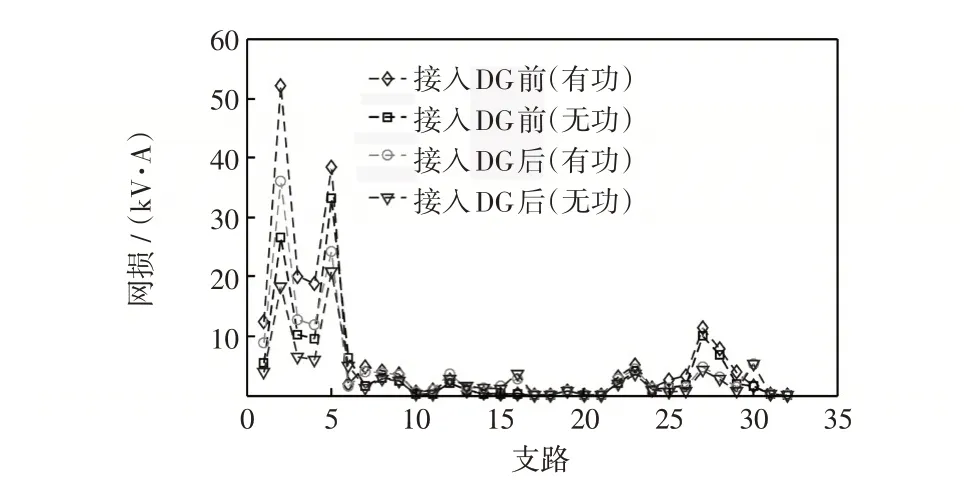
图13 接入分布式电源前后配电网的支路网损对比Fig.13 Comparison of branch loss in distribution network before and after the access of distributed generation

5.4 算法性能比较

为了验证本文算法的优越性，采用本文所提算法和文献[5]所提算法分别对本文算例进行仿真计算，得到的结果如表3所示。从表3中可知，本文所提算法规划的各项指标均较优，验证了本文算法的优越性。

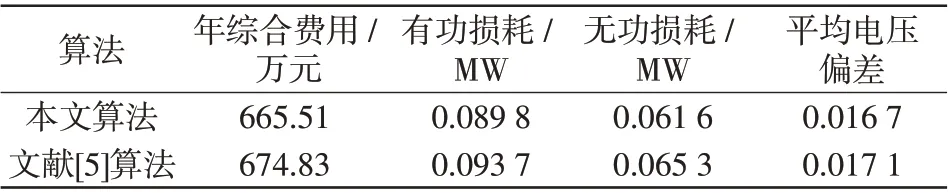
表3 不同算法规划结果Tab.3 Planning results of different algorithms

6 结 语

本文针对配电网规划中可再生分布式电源输出的随机性和间歇性导致的不确定性问题，提出了一种分布式电源选址定容模型。首先采用综合多种灵敏度指标的方法确定分布式电源安装候选节点顺序，以减小潜在求解空间的范围。然后采用启发式矩匹配法捕获历史场景的目标矩和相关性，得到风速、辐照、环境温度和负荷需求的代表性场景。最后基于生成的代表性场景，以年综合费用和平均电压偏差最小为目标，采用NSGA-Ⅱ算法进行优化求解，确定最佳的分布式电源接入位置和容量。以IEEE-33节点配电系统为例，按本文所提模型规划的结果接入分布式电源后，年综合费用和网络损耗均大幅减小，配电网的节点电压分布也得到了明显改善，验证了本文所提模型的有效性。