例谈培养学生分析提炼关键信息的能力
刘白生
(江苏省溧水高级中学 江苏 南京 211200)
笔者对学生的错题进行了深入的研究,探究其原因一个重要的因素是学生分析提炼关键信息的能力不够,而一些理想模型、理想状态、理想过程、临界条件等都隐含在关键信息中,解题过程中它们往往是关键,不能提炼出这些关键信息会导致学生做题有时无从下手,有时用错规律,这类错误也是一些优秀的学生成绩不够稳定的主要因素[1~3].本文试举几例说明培养学生分析提炼关键信息的能力是化解问题难点的关键.
1 关键信息中隐含理想模型
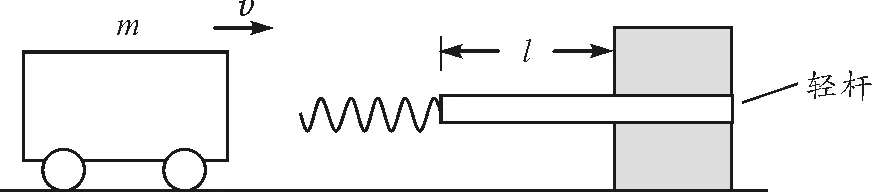
图1 例1题图
(1)若弹簧的劲度系数为κ,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v′和撞击速度v的关系.
分析:本题的关键信息是轻杆这一理想模型和它在受到外力作用时的特点及导致轻质弹簧在各种情况下会出现的状态.轻杆模型是指它的质量忽略不计,根据牛顿第二定律,轻杆模型受的合外力等于零,因为如果合外力不等于零其加速度为无穷大.本题中有一个轻杆,它受的合外力等于零,当它不滑动时,弹簧给它的弹力等于轻杆与槽间的静摩擦力;当它滑动时,弹簧给它的弹力等于轻杆与槽间的滑动摩擦力,为一定值,因此当小车以不同的速度撞击致使轻杆滑动时,弹簧的压缩量都是相同的,即小车对弹簧所做的功相同,从而储存的弹性势能相同.
解答:(1)轻杆开始移动时,弹簧的弹力
F=κx
且
F=f
解得

(2)设轻杆移动前小车对弹簧所做的功为W,则小车从撞击到停止的过程中,由动能定理可知小车以v0撞击弹簧时
(1)
小车以vm撞击弹簧时
(2)
解得
(3)设轻杆恰好移动时,小车撞击速度为v1,有
(3)
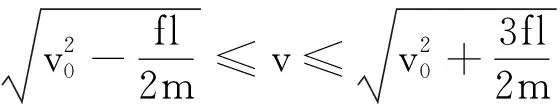
由式(1)和(3)解得
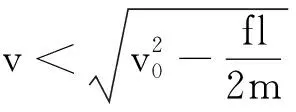
v′=v
2 关键信息中隐含理想状态
【例2】如图2所示,质量为m的物体(可视为质点)在水平传送带中央随传送带以速度v0匀速运动,在传送带上方固定光滑挡板AB,AB与传送带左边界的夹角为53°,物体碰到挡板时,垂直于挡板方向的速度减小为零,平行于挡板方向的速度不变,最终滑上工作台,已知传送带的宽度为L,物体与传送带之间的动摩擦因数为μ,重力加速度为g.取sin 53°=0.8,cos 53°=0.6.
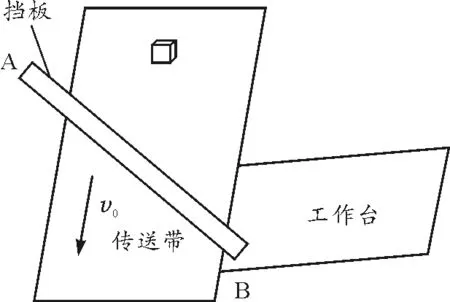
图2 例2题图
求物体:(1)与挡板碰撞结束瞬间速度的大小v;
(2)沿挡板运动过程中对挡板的压力F;
(3)沿挡板运动过程中与传送带间因摩擦产生的热量Q.
分析:本题的关键信息是物体碰到挡板后瞬间相对于传送带的速度方向这一隐含的理想状态.物体碰到挡板时,垂直于挡板方向的速度减小为零,平行于挡板方向的速度不变,对这一信息分析可知,若将传送带的速度分解为平行于光滑挡板和垂直于挡板二个分速度,则物体在平行于光滑挡板方向无相对运动,此时这个方向不受摩擦力,从而这个方向受的合力为零,速度不变,保持无相对运动.垂直于挡板方向有相对运动,物体受摩擦力作用,这个摩擦力为合摩擦力.
解答:
(1)将物体随传送带运动速度分解为沿挡板方向和垂直于挡板方向,如图3所示.则
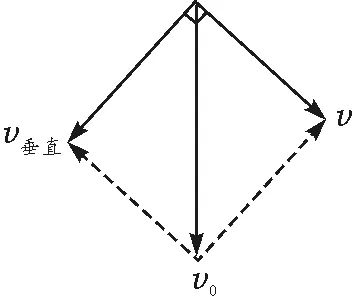
图3 例2解图
v=v0cos 53°=0.6v0
物体与挡板碰撞结束时速度的大小为0.6v0
(2)物体与挡板碰撞结束后,相对传送带速度大小
v相对=v垂直=v0sin 53°=0.8v0
方向垂直于挡板斜向后,物体水平面上受到传送带摩擦力与挡板弹力,大小相等,方向相反.
对物体水平方向
F支=Ff
由摩擦定律得
Ff=μFN
竖直方向二力平衡
FN=mg
由牛顿第三定律得
F压=F支=μmg
方向垂直于挡板斜向前.
(3)物体碰撞挡板后沿挡板做匀速直线运动,由几何关系得:
物体的位移
物体从碰到挡板到离开传送带的运动时间
物体从碰到挡板到离开传送带,相对传送带的位移
物体沿挡板运动过程中与传送带间因摩擦而产生的热量
3 关键信息中隐含理想过程
【例3】在原子核物理中,研究核子与核关联的最有效途径是“双电荷交换反应”.这类反应的前半部分过程和下述力学模型类似.两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态.在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向球B,如图4所示.C与B发生碰撞并立即结成一个整体D.在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变.然后,球A与挡板P发生碰撞,碰后A和D都静止不动,A与P接触而不粘连.过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失).已知A,B,C 3球的质量均为m.
(1)求弹簧长度刚被锁定后球A的速度.
(2)求在球A离开挡板P之后的运动过程中,弹簧的最大弹性势能.
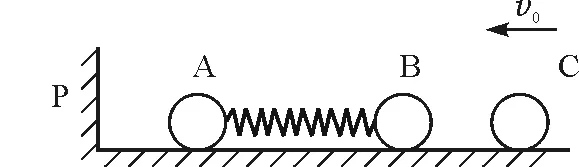
图4 例3题图
分析:本题的关键信息是在弹簧压至最短的过程中弹簧贮存势能,从解除锁定(锁定及解除锁定均无机械能损失)到球A离开挡板P的过程中A,D及弹簧组成的系统动量不守恒,在球A离开挡板P之后的运动过程中A,D及弹簧组成的系统动量守恒,机械能守恒这3个隐含的理想过程.
解答:(1)设球C与球B粘结成D时,D的速度为v1,由动量守恒,有
mv0=(m+m)v1
当弹簧压至最短时,D与A的速度相等,设此速度为v2,由动量守恒,有
2mv1=3mv2
由两式得A的速度
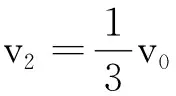
(2)设弹簧长度被锁定后,贮存在弹簧中的势能为Ep,由能量守恒,有
撞击P后,A与D 的动能都为零,解除锁定后,当弹簧刚恢复到自然长度时,势能全部转变成D 的动能,设D的速度为v3,则有
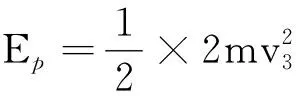
当弹簧伸长,球A离开挡板P,并获得速度.当A和D的速度相等时,弹簧伸至最长.设此时的速度为v4,由动量守恒,有
2mv3=3mv4
当弹簧伸到最长时,其势能最大,设此势能为E′p,由能量守恒,有
解以上各式得
4 关键信息中隐含临界条件
【例4】如图5所示,3个质量均为1 kg的物体A,B,C叠放在水平桌面上,B和C用不可伸长的轻绳跨过一光滑轻质定滑轮连接,A与B之间、B与C之间的接触面以及轻绳均与桌面平行,A与B之间、B与C之间以及C与桌面之间的动摩擦因数分别为0.4,0.2和0.1,重力加速度g取10 m/s2,设最大静摩擦力等于滑动摩擦力.用力F沿水平方向拉物体C,以下说法正确的是( )
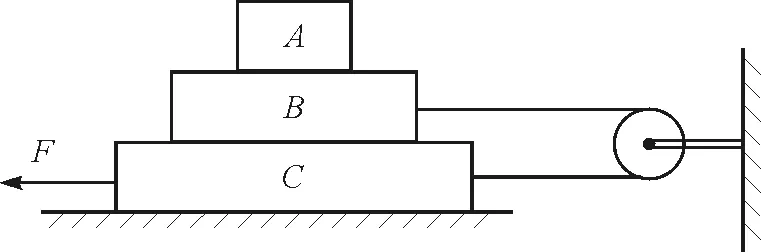
图5 例4题图
A.拉力F小于11 N时,不能拉动C
B.拉力F为17 N时,轻绳的拉力为4 N
C.要使A和B保持相对静止,拉力F不能超过23 N
D.A的加速度将随拉力F的增大而增大
分析:本题关键信息中隐含的临界条件是C向左运动,A和B共同向右运动的关系是它们的加速度大小相等,条件是加速度的大小大于等于零;A和B有相对运动时的临界条件是A所受的合力大于等于最大静摩擦力.把握这两个隐含的临界条件是解决这个问题的关键.
解答:
A.当C物体即将运动时,C物体水平方向桌面给C的向右的摩擦力f桌,绳子向右的拉力T,B给C向右的摩擦力fBC,其中
f桌=0.1(mA+mB+mC)g=3 N
fBC=0.2(mA+mB)g=4 N
当即将滑动时应有
F=f桌+fBC+T,T=fBC=4 N
可解得
F=11 N
故A正确.
C.因为B和C的加速度大小相等,在A和B即将发生相对滑动,对A受力分析可得
fAB=0.4mAg=mAa
对AB整体受力分析可得
T-fBC=(mA+mB)a
对C物体受力分析可得
F-T-fBC-f桌=mCa
联立解得
F=23 N
说明A和B发生相对滑动的临界力大小为
F=23 N
故C正确.
B.当F=17 N时,没有发生相对滑动,此时对AB整体
T-fBC=(mA+mB)a1
对C物体受力分析
F-T-fBC-f地=mCa1
联立解得
T=8 N
故B错误;
D.当拉力增大,A和B发生相对滑动时,则A物体受到滑动摩擦力,加速度为
a=0.4g=4 m/s2
加速度不变,D错误.
故选A,C.
由以上例题可以看出,分析提炼关键信息的能力对化解问题难点有着重要的作用,当然还有其他的一些关键点隐含在题目的信息中,在平时的练习中教师要注重选择这一类型的习题进行训练,并及时进行分析和点拨,当训练量达到一定的程度时,学生分析提炼关键信息的能力就形成了,学生就能比较顺利地解决类似的问题了,大家不妨试之.
——“模型类”相关试题选登

