基于Logit模型的水泥稳定碎石路用性能预测方法研究

杭争强，冯 琦，刘成安

(中电建冀交高速公路投资发展有限公司，河北省石家庄市桥西区城角街672号 050051)

水泥稳定碎石基层因具有承载能力强、耐久性好、稳定性能高等突出优点，多年来一直是我国沥青路面结构中最主要的基层类型。而在实际工程中，由于水泥稳定碎石基层在施工时受多种因素影响，其力学性能及耐久性都难以保障，因此有必要通过多种影响因素对水泥稳定碎石路用性能进行预测研究。然而水泥含量、温度以及养生龄期等因素与水泥稳定碎石路用性能密切相关，所以本文中通过水泥含量、温度以及养生龄期对水泥稳定碎石力学性能进行研究，从而对其路用性能进行预测。本研究对水泥稳定碎石基层施工具有重大意义，能够有效促进其施工质量的提高。

蒋应军等[1]通过研究表明水泥稳定碎石的水泥含量在5%以内时，水泥含量的提高对极限强度的影响效果显著，并且水泥稳定碎石材料强度随着龄期的增长而提高，龄期28d之前强度增长较为显著。王鹏飞、郭忠印等[2]采用正交法，分析研究水泥含量、集料含量等因素对7d无侧限抗压强度的影响，并通过分析表明了半刚性材料水泥稳定碎石具有良好的力学性能。田宇翔等[3]以水泥含量、养生温度与冻融循环次数为变量，研究得出了水泥稳定碎石强度在0～5次的冻融循环周期内下降较为明显，表明较高的水泥含量与养生温度对降低水泥稳定碎石冻融后的强度损失有明显的效果，因此，建议在工程中控制水泥含量为4%，同时养生温度大于10℃，以有效提高抗冻融性能。

综上所述，我国在水泥稳定碎石路用性能的影响因素方面已经做了一定的研究，但是缺少通过多个影响因素对水泥稳定碎石路用性能进行预测的研究。文中基于水泥稳定碎石无侧限抗压强度、劈裂强度和抗压回弹模量的试验结果，建立了有序变量累积Logit模型，最终对水泥稳定碎石基层的路用性能进行分析和预测。该研究成果有助于工程技术人员更好地对水泥稳定碎石的路用性能进行预测，从而更好地指导水泥稳定碎石基层施工,提高工程质量。

1 水泥稳定碎石路用性能预测指标选取

本模型采用水泥稳定碎石的力学性能作为路用性能评价指标，包括无侧限抗压强度、劈裂强度以及抗压回弹模量3个基本指标[4]，以水泥稳定碎石的水泥含量、温度以及养生龄期作为影响变量指标，建立综合的预测评价体系，具体的评价指标如表1所示。

表1 水泥稳定碎石路用性能影响因素评价指标Tab.1 Evaluation index of influencing factors of cement-stabilized macadam road performance

2 水泥稳定碎石路用性能预测模型建立

首先采用有序变量累积Logistic回归函数、有序变量累积Logit模型进行分析，不要求变量满足正态分布或等方差。模型中采用的Logistic函数为

式中：xi表示第i个指标；αi是第i个指标的系数；Y是因变量。

由于Y∈(0,1)，所以Y又常被理解为属于某一类或者某一范围的概率，如水泥稳定碎石基层力学强度中的无侧限抗压强度、劈裂强度以及抗压回弹模量的取值属于某一取值范围的概率。

以水泥稳定碎石基层力学强度指标无侧限抗压强度、劈裂强度以及抗压回弹模量为因变量的y1，y2，y3具有有序性，按照其有序性可以把y1无侧限抗压强度按照相应强度要求将其取值划分为5个评价范围。y2，y3则采用相同的评价范围划分方法。

有序变量累积Logit模型为：

qi=q(y=i)

i=1,2,…,c

=αi+βX

=αi+β1X1+…+βiXi

i=1,2,3，…

其中模型的各个自变量的回归系数β不会因为因变量的位置不同而发生改变。最后根据多元有序变量累积Logistic模型回归结果对水泥稳定碎石基层路用性能力学强度作出评判。

3 水泥稳定碎石路用预测模型应用分析

3.1 水泥稳定碎石路用性能试验

以《公路工程无机稳定结合料稳定材料试验规程》(JTG E51-2009)为标准，制作成型的试件在标准养生20℃条件和非标准养生(10℃，30℃)条件下养生3d，7d，14d，28d，并在养生期最后一天浸水养护，在标准强度试验机上测定其无侧限抗压强度、劈裂强度和抗压回弹模量[5-6]。研究中分别对3种不同水泥剂量(4%，5%，6%)的水泥稳定碎石试件进行了无侧限抗压强度试验、劈裂强度试验和抗压回弹模量试验，其中无侧限抗压强度、劈裂强度以及抗压回弹模量试验结果如表2、表3、表4所示。

表2 水泥稳定碎石无侧限抗压强度试验结果

表3 水泥稳定碎石劈裂强度试验结果

表4 水泥稳定碎石抗压回弹模量试验结果

3.2 基于Logit模型的水泥稳定碎石路用性能预测

通过对比数据分析发现：无侧限抗压强度数值大部分都集中在3～7MPa之间，还有一部分集中在1.5～3MPa之间，只有特别少的部分在7～10.5MPa之间。将水泥稳定碎石基层无侧限抗压强度划分为5个评价范围，对于水泥稳定碎石基层劈裂强度和抗压回弹模量的数值，采用相同的方式将劈裂强度和抗压回弹模量也分别划分为5个、6个评价范围[7-8]。各划分范围如表5所示。

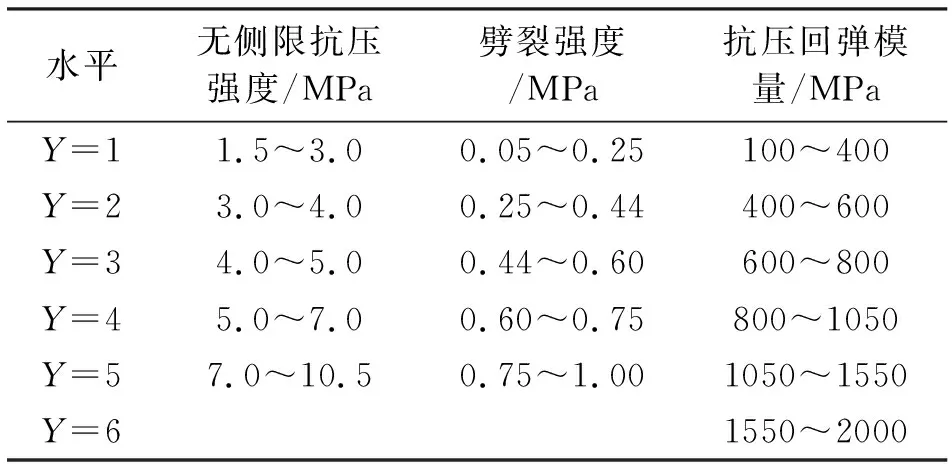
表5 水泥稳定碎石力学强度评价范围划分Tab.5 Division of evaluation level of mechanical strength of cement-stabilized macadam

最后应用Minitab软件对以上叙述表格进行计算，分别输入水泥稳定碎石基层无侧限抗压强度、劈裂强度以及抗压回弹模量的工作单数据文件，对于每一个单数据文件首先打开顺序Logistic回归分析主对话框，选择主对话框中的响应事件为响应变量Y，之后选择模型分别为养护温度、水泥含量及龄期3个，最后点击“确定”键进行计算，得出的最后的无侧限抗压强度结果如图1所示。

图1 无侧限抗压强度原始数据、回归系数、回归系数标准误差Fig.1 Raw data, regression coefficient and standard error of regression coefficient of unconfined compressive strength

Wald检验结果说明，自由度(自变量个数)DF=3，取“水泥含量”、“温度”和“养生龄期”作为自变量，各自的回归系数效应是显著的(p=0.000)。采用有序变量累积Logistic回归分析反应变量的划分类别与预测的精度要求有关，因为计算的全过程均采用Minitab软件来实现，所以采用此方法进行计算分析十分简单、便捷。

3.3 基于Logit模型的水泥稳定碎石路用性能预测结果分析

对于有序多分类Logistic回归分析，最常用的是累积Logistic回归模型，即：

=αi+βX

=αi+β1X1+…+βiXi

i=1,2,3,…，(水平数-1)。

由此可见，累积Logistic回归模型以“水平数-1”个回归方程描述多自变量与反应变量的关系，而它们的常数(αi)未必相同，但其回归系数β一定相同[9-10]。最后将所得的系数带入回归方程得出无侧限抗压强度、劈裂强度、抗压回弹模量的预测方程。

1)无侧限抗压强度预测方程

logit1[P(Y≤1|X1，X2，X3)]=32.2129-0.5452X1-4.1205X2-0.4984X3

logit2[P(Y≤2|X1，X2，X3)]=36.8177-0.5452X1-4.1205X2-0.4984X3

logit3[P(Y≤3|X1，X2，X3)]=41.5391-0.5452X1-4.1205X2-0.4984X3

logit4[P(Y≤4|X1，X2，X3)]=47.4223-0.5452X1-4.1205X2-0.4984X3

2)劈裂强度预测方程

所谓的文化资本可以分为身体化、客观化以及制度化。家庭环境可以说是学生得到文化资本的关键场所。家庭所具备的文化资本，将决定了学生在这个家庭当中所能够得到的文化资本的质量。而学生在家庭环境当中所得到的文化资本，对于他们在学校当中的学习将会产生非常关键的深远的影响。

logit1[P(Y≤1|X1，X2，X3)]=62.3561-1.5153X1-6.1440X2-0.7460X3

logit2[P(Y≤2|X1，X2，X3)]=75.2667-1.5153X1-6.1440X2-0.7460X3

logit3[P(Y≤3|X1，X2，X3)]=84.2704-1.5153X1-6.1440X2-0.7460X3

logit4[P(Y≤4|X1，X2，X3)]=89.6478-1.5153X1-6.1440X2-0.7460X3

3)抗压回弹模量预测方程

logit1[P(Y≤1|X1，X2，X3)]=21.5373-0.3602X1-2.4378X2-0.8444X3

logit2[P(Y≤2|X1，X2，X3)]=25.1018-0.3602X1-2.4378X2-0.8444X3

logit3[P(Y≤3|X1，X2，X3)]=28.6338-0.3602X1-2.4378X2-0.8444X3

logit5[P(Y≤5|X1，X2，X3)]=43.6507-0.3602X1-2.4378X2-0.8444X3

现在对得出的无侧限抗压强度、劈裂强度、抗压回弹模量预测方程分别进行验证。从样本数据中随机抽取一组数据进行验证，所抽取的数据为X1=10℃，X2=6%，X3=28d，将其分别代入无侧限抗压强度、劈裂强度、抗压回弹模量相对应的预测方程。

1)无侧限抗压强度

P[P(Y≤1|X1，X2，X3)]=6.7×10-6

P[P(Y≤2|X1，X2，X3)]=0.0007

P[P(Y≤3|X1，X2，X3)]=0.07

P[P(Y≤4|X1，X2，X3)]=0.96

可见，相应于抽取的数据X1=10℃，X2=6%，X3=28d，水泥稳定碎石基层无侧限抗压强度的预测结果为：Y=1(1.5～3.0MPa)的概率值为6.7×10-6，Y=2(3.0～4.0MPa)的概率值为0.00007，Y=3(4.0～5.0MPa)的概率值为0.07，Y=4(5.0～7.0MPa)的概率值为0.96，Y=5(7.0～10.5MPa)的概率值为0.04。可以看出，Y=4(5.0～7.0MPa)的概率值最高，因此水泥稳定碎石基层的无侧限抗压强度值极大可能集中在5.0～7.0MPa之间。根据在抽取的3个反映自变量条件下无侧限抗压强度的实测值为5.31MPa，上述4个水泥稳定碎石基层无侧限抗压强度预测方程符合要求。

2)劈裂强度

P[P(Y≤1|X1，X2，X3)]=0.00003

P[P(Y≤2|X1，X2，X3)]=0.91

P[P(Y≤3|X1，X2，X3)]=0.99

P[P(Y≤4|X1，X2，X3)]=1

可见，相应于抽取的数据X1=10℃，X2=6%，X3=28d水泥稳定碎石基层劈裂强度的预测结果为：Y=1(0.05～0.25MPa)的概率值为0.00003，Y=2(0.25～0.44MPa)的概率值为0.909，Y=3(0.44～0.60MPa)的概率值为0.08，Y=4(0.60～0.75MPa)的概率值为0.01，Y=5(0.75～1.00MPa)的概率值为0.00097。可以看出，Y=2(0.25～0.44MPa)的概率值最高，因此水泥稳定碎石基层的劈裂强度值极大可能集中在0.25～0.44MPa之间，根据在抽取的3个反映自变量条件下劈裂强度的实测值为0.40MPa，上述4个水泥稳定碎石基层劈裂强度预测方程符合要求。

3)抗压回弹模量

P[P(Y≤1|X1，X2，X3)]=1×10-8

P[P(Y≤2|X1，X2，X3)]=5.2×10-8

P[P(Y≤3|X1，X2，X3)]=.18×10-6

P[P(Y≤4|X1，X2，X3)]=0.0002

P[P(Y≤5|X1，X2，X3)]=0.86

可见，相应于抽取的数据X1=10℃，X2=6%，X3=28d水泥稳定碎石基层抗压回弹模量的预测结果为：Y=1(100～400MPa)的概率值为1×10-8，Y=2(400～600MPa)的概率值为5.2×10-8，Y=3(600～800MPa)的概率值为1.8×10-6，Y=4(800～1050MPa)的概率值为0.0002，Y=5(1050～1500MPa)的概率值为0.86，Y=6(1500～2000MPa)的概率值为0.1399。可以看出，Y=5(1050～1500MPa)的概率值最高，因此水泥稳定碎石基层的抗压回弹模量值极大可能集中在1050～1500MPa之间。根据在抽取的3个反映自变量条件下抗压回弹模量的实测值为1190MPa，上述5个水泥稳定碎石基层抗压回弹模量预测方程符合要求。

4 结论

通过在不同温度(10℃，20℃，30℃)，掺加不同水泥含量(4%，5%，6%)的水泥稳定碎石分别在不同的养生龄期条件下进行无侧限抗压强度、劈裂强度、抗压回弹模量试验，运用有序变量累积Logit模型，得出水泥含量、温度以及养生龄期对水泥稳定碎石路用性能的影响变化规律，主要结论如下。

(1)文中将有序变量累积Logistic回归模型运用到水泥稳定碎石路用性能预测中，并通过对水泥稳定碎石基层路用性能概率预测模型进行检验，验证得出结论：该模型能够较为精确地对水泥稳定碎石基层的路用性能进行预测，在未来道路施工中对水泥稳定碎石路用性能的提前掌握提供理论方法，指导工程实践。

(2)由于本次模型的建立所选取的数据是通过室内试验记录得到的实测数据，用于模型计算的实测数据样本相对来说较少。若要得到一定精度的水泥稳定碎石基层的路用力学性能指标预测值，则需要给出一定量的实测数据，用于模型拟合的实测数据越多，预测值就越精确。