基于IALO-ELM模型的滚动轴承故障诊断方法

朱建府 李 亚

（昆明理工大学信息工程与自动化学院）

轴承的运行状态与机械设备的工作效率息息相关［1］。旋转机械故障中的30%～40%是由轴承的不良运行状态引发的［2］，由于滚动轴承的运行环境复杂，在运行过程中受负载、冲击等其他非线性条件的干扰，其振动信号通常表现为非平稳和非线性特性［3］，所以发生故障的概率也较高。 为此，笔者采用变分模态分解（VMD）［4］对采集到的原始振动信号进行分解并提取有效的分量作为信号特征向量。 采用极限学习机（ELM）作为故障诊断模型对轴承状态实施分类识别时， 由于ELM 输入权值参数与隐含层阈值参数的选择具有随机性，因此会对模型的诊断效果产生比较大的影响，故欲采用蚁狮优化算法 （Ant Lion Optimizer，ALO）对ELM 的随机参数进行优化处理， 从而有效提升ELM 的泛化能力和识别准确度， 进而构建良好的分类模型， 但ALO 算法易陷入局部最优且收敛速度慢， 因此采用柯西高斯变异进行改进。随后，将选取到的有效特征向量导入已构建好的分类模型中学习训练，得到训练好的极限学习机诊断模型IALO-ELM， 使用已训练好的分类模型对滚动轴承的工况进行识别诊断。

1 基本理论介绍

1.1 标准蚁狮优化算法

蚁狮是一种以捕食蚂蚁为生的肉食性昆虫，在捕食之前， 蚁狮会修建一个锥形的捕猎陷阱，随后藏在陷阱底部等待猎物，当随机游走的猎物落入陷阱后，为防止猎物逃跑，蚁狮会立刻向周围刨土，使猎物滑向阱底，进而将其捕食，随后蚁狮会重新修建陷阱准备下一次捕猎。

Mirjalili S 受自然界中蚁狮捕食蚂蚁行为的启发，提出一种新的群智能优化算法ALO［5］。 通过对比其他群智能优化算法，ALO 具有原理简单、变动参数少、调节参数少及准确度高等优点，展现了更好的收敛性和鲁棒性。

ALO 中，蚁狮通过不断捕猎高适应度的蚂蚁来求问题的最优解，现阐述其具体的捕食过程。

步骤1 蚁狮修建陷阱。 首先通过轮盘赌的方式选出一只蚁狮，被选出的蚁狮开始为捕食猎物修建陷阱，此方法可以增加蚁狮捕获蚂蚁的机会。

步骤2 蚂蚁随机游走。 蚂蚁在搜索领域觅食而随机移动的数学表达式为：

为了确保蚂蚁能在搜寻空间范围内随机游走，对其进行统一转换，即有：

步骤4 蚂蚁滑落阱底。 当蚂蚁滑落入圈套后，蚁狮向周围刨土，将试图逃跑的猎物滑入到阱底，这个过程可以看作蚂蚁绕蚁狮游走的半径在不断缩小，此行为的数学表达式为：

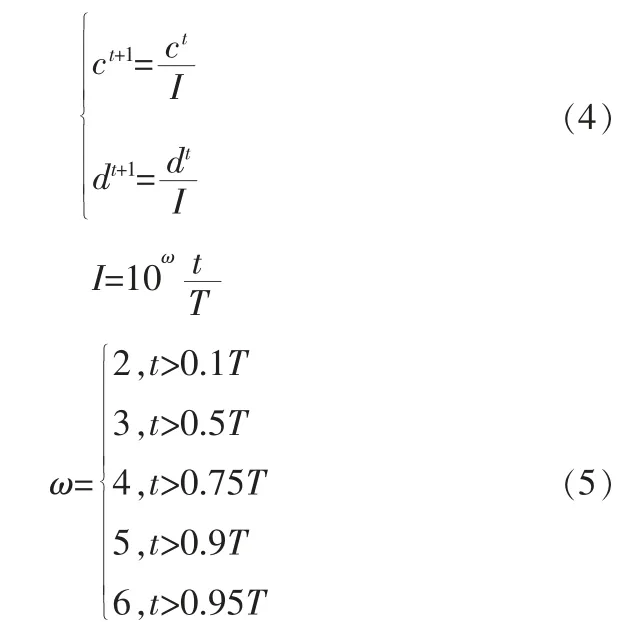
其中，ω 为常数，I 是比率。

步骤5 蚁狮重筑陷阱。 如果蚂蚁种群中存在适应度值更好的蚂蚁， 该蚂蚁被蚁狮捕食后，其位置将会作为新一代蚁狮的陷阱位置，以提高自身捕获猎物的机会，该过程数据表达式为：

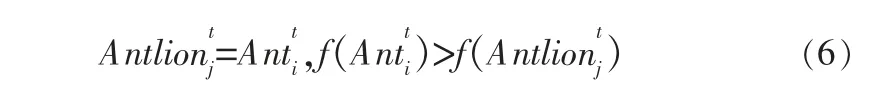
其中，f（）为适应度值函数。

步骤6 精英蚁狮。 精英蚁狮是每次迭代更新陷阱以后保留下来的最优蚁狮，由于蚁狮通过不断捕食蚂蚁来更新自己的位置，所以也可以看作是适应度最好的蚂蚁。 作为精英蚁狮，它在迭代过程中能够影响所有蚂蚁的运动。 因此，假设每只蚂蚁随机游走同时受轮盘赌策略和精英蚁狮的影响，精英的选择过程表达式为：

其中，RtA为第t 次迭代过程中按照轮盘赌的方法选中的绕蚁狮随机游走的蚂蚁群体，RtE为第t 次迭代过程中绕精英蚁狮随机游走的蚂蚁群体。

1.2 改进ALO

ALO 中，受精英蚁狮的影响，蚂蚁的收缩性移动可以确保整个算法过程的收敛性，而采用轮盘赌策略则有利于增强蚂蚁群体的全局寻优性能。 随着迭代次数的增加，蚁狮的捕食范围会逐渐变小， 进而使得蚂蚁种群的多样性不断下降。针对ALO 的不足，采用柯西高斯变异有效增加种群的多样性［6］，在很大程度上提高了算法的全局搜索能力、收敛精度和速度。

柯西分布的密度函数定义如下：

利用柯西分布的特点对ALO 加以改进，将柯西分布的随机向量用于精英蚁狮个体的状态上，变异的具体表达式为：

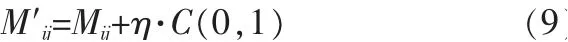
其中，M′ij表示初始位置Mij的更新位置，η为控制变异步长的常数，C（0，1）是由t=1 时的柯西分布函数生成的随机数。

当算法进入循环迭代后，迭代最优值会被记录下来，当相邻的两次迭代产生的最优值几乎相同时，认为算法掉入局部陷阱，此时进行柯西高斯变异。

变异操作。 先将最优蚁狮的适应度值和个数复制到原始的种群规模，然后引入柯西高斯变异算子更新蚁狮群体的位置和最优值，具体如下：

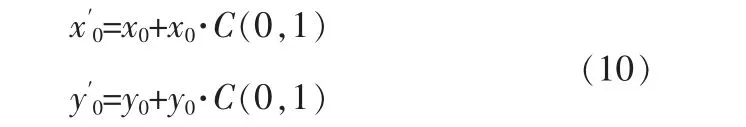
其中，x0、y0为原个体位置，x′0、y′0为经过变异后的新位置。

1.3 ELM

ELM 作为一种简单易用的神经网络（图1）［7］，具有参数选择方便、学习效率高及泛化性能优等特点［8］。 ELM 中只有隐含层的节点数需要人为设置，而输入层与隐含层之间的权值参数和隐含层的 阈 值 参 数 都 是 随 机 生 成 的［9，10］，而 且 在 进 行 训练的过程中不需要任何调整，这样就避免了迭代过程调整神经网络参数的繁琐步骤，相比于传统的神经网络，ELM 具有更高的效率。

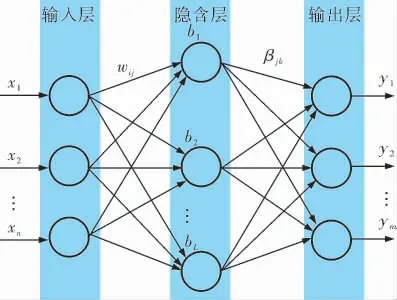
图1 ELM 网络结构

对 于N 个 任 意 不 同 样 本（Xi，ti）（Xi=［xi1，xi2，…，xin］∈Rn，ti=［ti1，ti2，…，tim］∈Rm)，存在L 个隐含层节点的ELM 网络模型为：

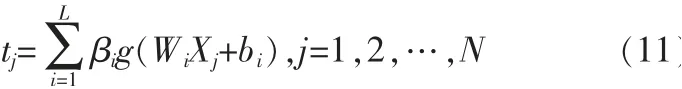
其中，Wi为输入权重矩阵，bi为隐含层第i个节点的阈值，g（x）为激活函数，βi为输出权重。将式（11）表示为矩阵形式：

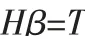
对输入权值参数和阈值参数初始化后，隐含层输出矩阵H 便可确定， 输出权值矩阵可计算为：

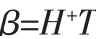
其中，H+为H 的Moore-penrose 广义逆矩阵［11］。这样，整个ELM 网络的结构就被确定了。

2 用改进的ALO 优化ELM

由于ELM 的输入层权值参数和隐含层阈值参数都是随机产生的，这就导致隐含层的节点数逐渐增加，致使算法的识别精度降低［12］。 为此，采用改进的ALO（IALO）对ELM 的输入层权值参数与隐含层阈值参数进行筛选，选取最优的参数组合，从而增强ELM 的学习能力与泛化性能，以实现最优的诊断效果。 IALO 优化ELM 的流程如图2 所示。

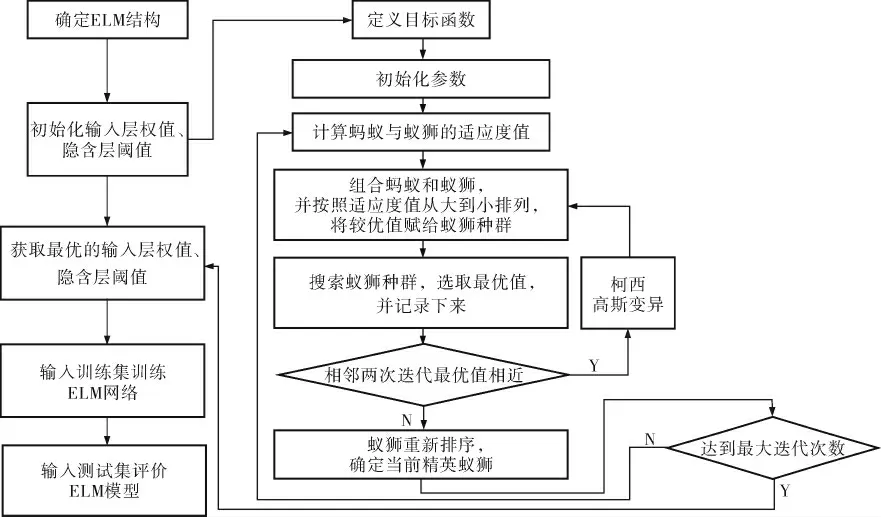
图2 IALO 优化ELM 的流程

3 试验与结果分析

为证明笔者所提方法的实用性，试验所用数据来自美国凯斯西储大学轴承数据中心网站。

首先采用VMD 方法对原始数据进行分解，选取有效分量进行信号重构，最终获得正常运行状态、内圈故障、外圈故障和滚动体故障4 种信号的特征向量。 试验过程中，将4 种状态信号（1正常信号，2 内圈故障，3 外圈故障，4 滚动体故障） 共4 800 个样本分别划分为训练样本和测试样本，每种状态信号的80%作为训练样本，剩下的20%作为测试样本。

为了验证笔者所提方法的优越性， 分别采用遗传算法（GA）、粒子群算法（PSO）和ALO 对ELM的输入层权值与隐含层阈值进行优化， 并与笔者所提方法对比。基于有效性和公平性的考虑，将算法中涉及的种群数目设置为90， 迭代次数最大值设置为100。 4 种算法的适应度曲线如图3 所示。

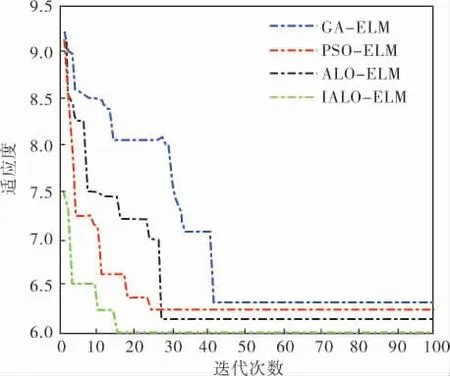
图3 4 种算法的适应度曲线

由图3 可以看出，GA-ELM 算法在40 代左右收敛，与其他3 种算法相比，其收敛速度与寻优结果并不是很理想。 PSO-ELM 算法在24 代左右趋于收敛，相比于GA-ELM，收敛速度要快，但寻优结果较之略逊。ALO-ELM 寻优结果要好于GAELM，但是收敛速度慢了些。IALO 在ALO 的基础上融合了柯西算子，有效解决了ALO 容易陷入局部最优的问题， 从而提高了收敛速度与学习效率，IALO-ELM 在15 代左右就趋于收敛并获取了最优值，收敛速度与寻优结果要优于其他3 种算法。

4 诊断模型比较

为了验证IALO 优化ELM 参数的高效性，现选取支持向量机 （SVM）、ELM、ALO-ELM 和IALO-ELM4 种诊断模型进行故障诊断准确度的对比，将这4 个诊断模型分别独立运行6 次，记录下每种模型各次的诊断结果，如图4 所示。

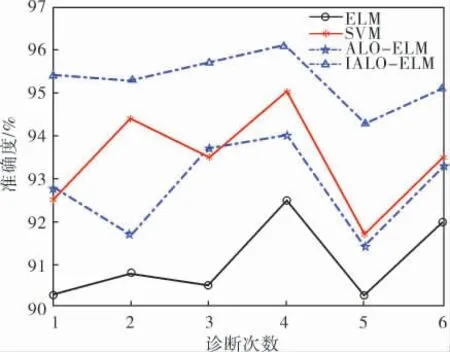
图4 4 种分类模型的准确度比较

为了凸显IALO-ELM 的诊断效果，统计4 种诊断模型的训练时间和测试时间，详见表1，可以看出，IALO-ELM 的训练速度比ELM 要慢， 这是ELM 在诊断过程中随机选定参数的结果。综合诊断时间与准确度两大重要指标，IALO-ELM 模型要明显优于其他诊断模型。 证实IALO-ELM 模型在滚动轴承故障诊断中具有良好的性能，而且稳定性较高。

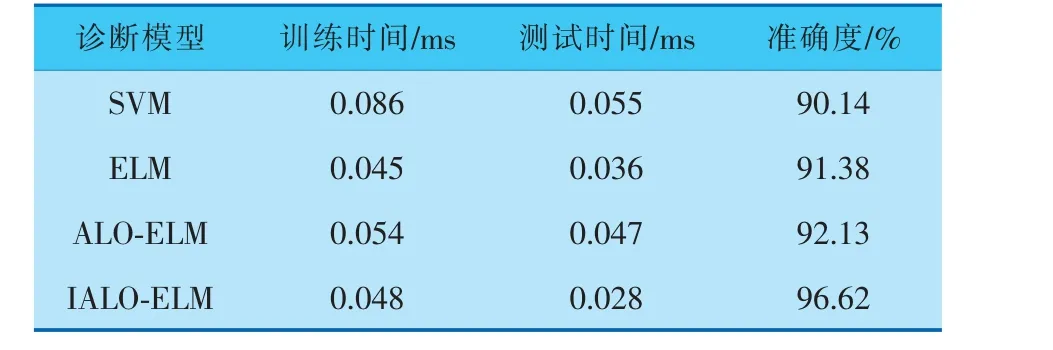
表1 4 种诊断模型的训练时间和测试时间

5 实际样本与诊断值的比较

为了验证IALO-ELM 模型对滚动轴承故障的分类准确度，将测试数据集输入到已经学习好的诊断模型中进行诊断，并与实际输出样本进行比较，结果如图5 所示，可以看出，识别准确度能达到96.625%。

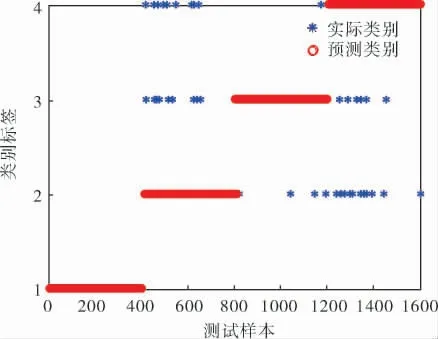
图5 IALO-ELM 模型的分类准确度

6 结束语

采用IALO 对ELM 的参数进行优化筛选，选取最优的参数组合建立良好的故障诊断模型。 通过试验对比分析显示，IALO-ELM 模型在滚动轴承故障诊断中具有更高的预测精度，说明该模型有较好的实用性。