南京某市政道路土石混合路基填料压实特性数值模拟分析

薛鹭鹭

摘 要：为简化路基填料压实度测量时间与费用，本文以南京某市政道路为研究对象，借助二维颗粒模拟技术，即PFC2D进行压实度数值模拟，详细研究了路基填料的压实过程与接触力链的变化情况，经与实测值对比分析，5个测点压实度的计算误差率在-0.135%～0.023%范围内，误差较小，计算精度较高，能很好地反映实际的压实度情况。最后，基于大量实测值建立了道路土石混合填料的EVD的预测模型计算公式。本文研究结果可为同类市政工程土石混合填料的压实计算提供参考与借鉴。

关键词：道路填料压实特性;数值模拟分析;计算精度比较;EVD预测模型

0 前言

南京江宁地区地基土中碎石、岩体颗粒含量较高，由于碎石、岩体颗粒硬度高、透水性好、单价低廉，是一种良好的路基填筑材料，被广泛应用于南京市的相关道路工程路基铺筑建设中。同时，在实际应用过程中，由于南京江宁地区的碎石含量占比较大，一般可达到20%以上，且粘粉粒含量小于5%，因此粘聚力较差。根据《城市道路设计规范》[CJJ37.2012]，必须对土石混合填料含量的路基进行压实度检测。目前常用的检测方法有灌砂法和灌水法。这两类方法检测需要时间较长，需要消耗较多的人力、物力资源，影响工期进度。为研究快速检测的方法，本文以南京某市政道路为研究对象，借助二维颗粒模拟技术，即PFC2D进行压实度数值模拟。

1 实例工程概况

实例工程位于江宁高校区，路线全长约5.28 km，其中道路红线宽为40 m。道路横断面布置为双向6 车道，规划为城市主干路，设计速度为60 km/h。工程所在区域地层土体中，红黏土和中风化白云岩的含量较高。

2 PFC2D数值模拟计算

2.1 计算流程原理

PFC2D的力学原理是根据牛顿第二定律等经典力学，根据颗粒之间的作用力和反作用力确定相对位移，经过迭代循环，达到所有颗粒之间的平衡和稳定。

2.2 计算参数设定

根据实例工程的实际情况输入颗粒的总质量、每级颗粒组成所占的百分比含量、颗粒数目（根据该级颗粒的总质量、平均粒径推求颗粒数目）、颗粒重度、颗粒孔隙率、含水率、承载力参数等相关参数。

2.3 级配颗粒生成及加载

根据实例工程的实际情况，进行建模分析。在实例工程中，碎石、岩体颗粒形状为不规则分布，其中值粒径与最大粒径比值基本在0.35～0.40范围内。为保证模型计算收敛性同时减少计算量，将碎石、岩体颗粒简化为长宽比为1.0～1.8的圆形或椭圆形颗粒。

在PFC2D模型里生成级配颗粒图，机进行振动压实工况下，简偕振动力加载过程。

2.4 压实过程数值模拟

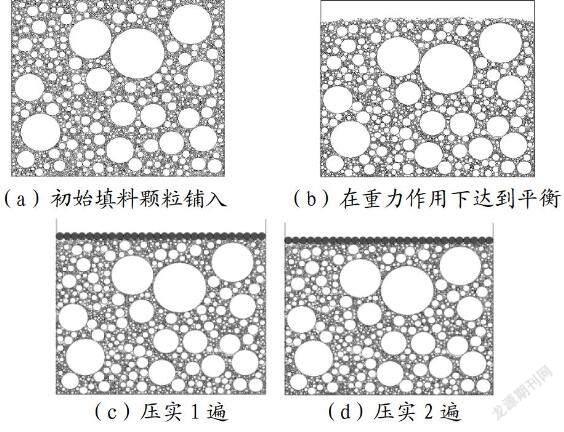
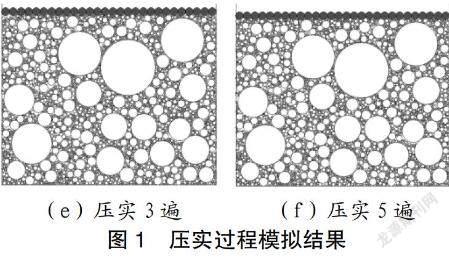
根据实例工程的实际情况模拟压实过程，模拟结果见图1。压实1遍至5遍的过程见图1（a）至图1（f）。分析可知：

（1）壓实的过程实质是填料颗粒重新排列和藿香填充的过程，随着压实遍数的增加，单位体积内的颗粒数量增加，密实度增大，孔隙率大幅下降，硬度和承载力也显著提升。

（2）实例工程在压实一遍之后，压实度达到75%的颗粒为92.35%;平均值为94.22;实例工程在压实两遍之后，压实度达到75%的颗粒为95.38%;平均值为96.17;实例工程在压实三遍之后，压实度达到75%的颗粒为95.65%;平均值为96.35;实例工程在压实五遍之后，压实度达到75%的颗粒为95.83%;平均值为96.68。

由此可见，在压实两遍之后，实例工程土体已基本完成压实、固结，孔隙率基本趋于0，再被压实的空间较小。

可见压实2～3遍可以满足设计压实度要求，且最为经济合理。

3 数学模型计算精度分析

根据实例工程实际压实过程与测量结果，分析本文数学模型计算的精度。

3.1 压实度数模计算精度分析

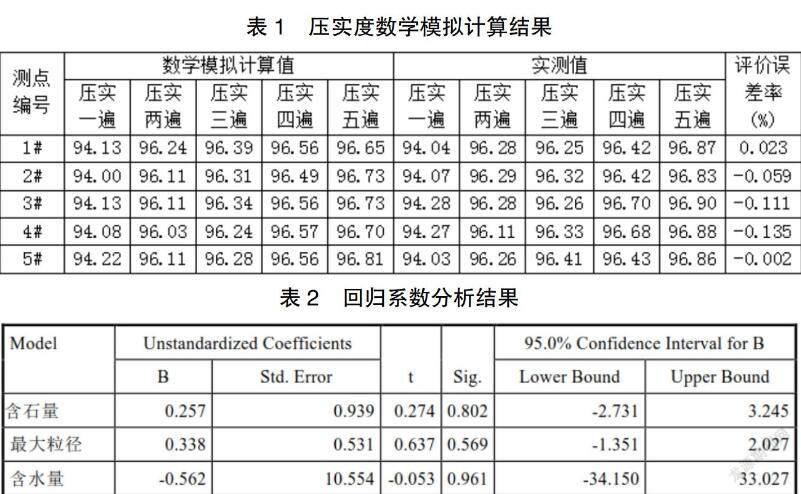
在实例工程中选择5个测点，各压实遍数情况下，压实度的模拟值与计算值统计结果见表1。分析表1可知，各测点压实度的计算误差率在-0.135%～0.023%范围内，误差较小，计算精度较高，能很好地反映实际的压实度情况。

3.2 压实度预测模型建立

根据实测结果，对所测压实度进行分区，取压实度范围处于[93.5，94.5]的测点视为94区。在5%的置信区间下进行回归分析，分析结果如表2。

因此，可得到EVD的预测模型计算公式如下：

（式1）

式中，为含石量;为最大粒径;为含水量。

4 结论

本文以南京某市政道路为研究对象，借助二维颗粒模拟技术，即PFC2D进行压实度数值模拟，得到以下结论：

（1）实例工程在压实两遍之后，实例工程土体已基本完成压实、固结，孔隙率基本趋于0，再被压实的空间较小。

（2）在满足设计压实度要求的前提下，实例工程进行2～3遍压实作业最为经济合理。

（3）经与实测值对比分析，5个测点压实度的计算误差率在-0.135%～0.023%范围内，误差较小，计算精度较高，能很好地反映实际的压实度情况。

（4）基于实测值建立了EVD的预测模型计算公式。

参考文献：

[1]项伟圆.粗粒料振动压实影响因素的数值模拟[D].江苏：东南大学，2007.

[2]杨荫华.土石料压实和质量控制[M].北京：中国水利水电出版社，1992：25-28.