程序类竞赛中的动态规划算法探讨

卢扬城，毛玉萃，关泽群

摘要：动态规划问题在各类程序设计竞赛中常常出现。该文首先简单介绍了动态规划算法，阐述了利用动态规划解决实际问题的流程，并通过实例进一步探讨了线性动态规划、区间动态规划、树形动态规划、背包动态规划以及状态压缩动态规划算法问题，简单介绍了动态规划算法思想在其他经典算法中的应用，最后进行了简单总结。

关键词：动态规划;程序类竞赛;实例;

中图分类号：TP311.52      文献标识码：A

文章编号：1009-3044（2021）21-0093-04

开放科学（资源服务）标识码（OSID）：

1 动态规划算法的概述[1-2]

动态规划算法在是许多算法的理论基础，在传统决策性问题、图论问题、字符串问题等问题中都有涉及，因此是程序设计类竞赛考察的重点。

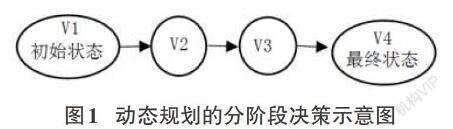
动态规划算法的核心是利用记忆化处理方式、依托贪心思想、记录历史数据来达到优化时间复杂度的目的，简而言之就是“用空间换时间”;在求解过程中采用分治思想，对问题分阶段进行决策。图1所示为动态规划的分阶段决策。

动态规划算法需要满足以下几个特征：

1.1 无后效性

无后效性是指当前状态一旦确定，则之后的所有状态与之前的情况无关，仅仅与当前状态的决策有关，因此要着重研究当前状态。

1.2 最优子结构

动态规划算法经常解决的是最值性问题。最优化子结构保证各阶段求解的方案决策具有类似的最值结构，即决策满足贪心思想下的解也一定是子解的最优解。

1.3 子问题重叠

即所分解得到的子问题之间不是相互独立的，在之后的阶段还可能被多次使用到。这一点不是动态规划算法适用的必要条件，但是如果没有这个特征，动态规划算法便不具有时间上的优势。

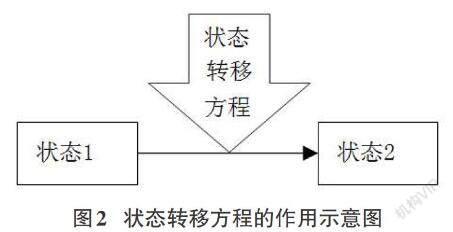
动态规划算法中状态定义和状态转移方程设计是核心。状态定义是解决动态规划问题的关键，把问题分成几个不同的情况对这些情况的抽象描述即是状态定义。状态转移方程是决策问题中的指南针，设计正确的状态转移方程是求解问题的重中之重，图2表示状态转移方程的作用。各阶段状态由历史状态转移而来，从众多的历史状态中选择哪一个就是状态转移方程要解决的任务。

2 动态规划求解问题的流程[1-4]

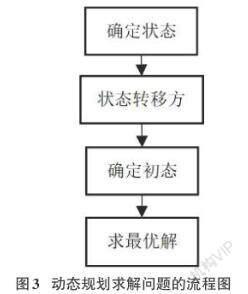
动态规划算法由其分阶段性和依托性，可将其分为正向递推和反向递推，利用分治思想从小问题逐渐递推到大问题，注意递推过程的逻辑性，观察不同状态间的特征及其之间的内在逻辑、不同点和相同点来得出初步递推公式。正向递推通常从“当前状态可以得到哪些状态”的大致思路思考，反向递推通常由“当前状态可以由哪些状态得到”的大致思路来思考。捋顺递推过程是解决动态规划问题十分关键的一步，确定了递推关系才能解决整个问题，递推关系的体现就是状态转移方程。动态规划求解问题的过程如图3所示。

首先确定状态就是根据问题描述中的信息整理出相关的量，这些量必须是相互独立的，也就是说在逻辑上问题的状态由这些量构成，缺少任意一个量状态问题的表示就不明确，在确定状态量时必须兼顾内存空间的要求，不能一味地追求细致刻画状态，而造成冗余状态的表示和无用信息的附加，这在动态规划算法优化部分着重介绍;其次确定基本量、依托量。基本量通常以题干给定的信息为主，在不需要推导的情况下就可以得到。依托量通常是抽象量，指的是我们对答案的构成描述，依托量的某个状态的全集就是最终的答案。再次根据问题描述中给定信息寻找不同量之间的递推关系，可以运用正向递推的方式也可以运用反向递推的方式，通常情况下较难的题涉及的递推思想常常与反向递推有关，确定了递推公式，接下来可以描述出状态转移方程的大致轮廓。许多涉及数组间递推的动态规划问题中，常见到以数组下标为基本量，以原数组数值为依托量来确定其递推关系。描述了状态转移方程之后要确定状态的初始情况，即确定初态，初态必须合乎状态转移方程的逻辑要求，初态的确定对算法来说有着举足轻重的作用。最后要确定哪些状态集合包含答案，通过遍历该集合得到答案。

3 各类动态规划的解题思路和应用举例

动态规划问题按其状态转移方程的形态和存儲方式，可以划分为线性动态规划、区间动态规划问题、树形动态规划问题、背包动态规划问题和状态压缩动态规划[1，3-5]。

3.1 线性动态规划

线性动态规划包含了动态规划的最基本的思想，是在线性结构上进行状态转移的，是最简单的动态规划，该类动态规划空间复杂度一般为O（n），问题大多较为简单。其他复杂类型的动态规划都是在它的基础上增加优化算法、增加状态维度和在各种抽象数据结构上等的模型。

例1（原题见参考文献[6]）问题简述：一个游戏由一个棋盘和一些棋子组成，所有的棋子都用一个正整数或“开始”或“结束”来标记。玩家从起点开始，最后必须跳到终点。在跳跃过程中，玩家将访问路径中的棋子，但每个人必须从一个棋子跳到另一个绝对大的棋子（假设起点是最小值，终点是最大值）。所有玩家都不能倒退。一跳可以从一个棋子跳到下一个棋子，也可以跨越多个棋子，甚至可以从起点直达终点。一个球员是赢家，当且仅当他能得到一个更大的分数，根据他的跳跃解决方案。一个玩家的分数来自他跳跃路径中棋子上的值的总和，求最大分数是多少。

这题是一道最长上升子序列的模板题。

子序列与子数组是区别。子序列指的是由原序列删除若干元素后，剩下的元素由相对位置不变的方式得到的一个有序集合。子数组是原序列上一段连续的有序集合。

此问题可以说是动态规划入门的经典问题并且是一个线性动态规划。假设数组为sl，设到sl[i]的最长长上升子序列的长度为dp[i]，最初dp[i]=1，即到sl[i] 的最长上升子序列的长度初始值1，即数组中的每一个数都是包含自身的一个数的最长上升子序列 。考虑状态转移方程的确定，在计算dp[i]的值之前，就已经计算出sl[i]前面的最长上升子序列的长度。当数sl[i]大于往前遍历到的数sl[j]时（j