基于凸优化的傅里叶叠层成像技术研究

胡跃辉，房国庆,2，方 勇，姚子贤,2，岳明强,3，张 涛

（1.特种显示技术国家工程实验室，合肥工业大学 光电技术研究院，安徽 合肥 230009；2.合肥工业大学电子科学与应用物理学院，安徽 合肥 230009；3.合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009；4.合肥溪流光电科技有限公司，安徽 合肥 230009）

引言

在人类科学技术发展史上，光学显微技术一直有着非常重要的地位，在未来的科技发展方向上高分辨率也是光学显微技术不断追求的目标之一。然而高分辨率和大视场一直是难以兼顾的问题，这给显微技术的发展带来了很大的限制。

傅里叶叠层显微成像技术（fourier ptychographic microscopy，FPM）是一种可以同时兼顾高分辨率和大视场的一种成像技术，利用相位恢复算法成功恢复出样本的高分辨率图像。1969年，Hoope等人提出了叠层成像技术[1-3]，在此基础上Zheng在2013年提出了FPM[4-6]。

已有研究表明CCD 采集的低分辨率图像对高分辨率图像的重构质量有着直接的影响[7]。为解决这一问题，2015年清华大学张永兵课题组提出了用超分辨率重建图像的方法[8]，但需要采集大量的原始图像，会使采集端的时间损耗加大，而传统去噪算法的缺陷在于会导致图像原始信息的丢失，严重影响着重建图像质量。因此我们引入了凸优化算法，将采集端低分辨率图片的去噪处理转为一个凸问题，进而用迭代收缩阈值算法来求解该凸问题，在迭代收缩阈值算法中，我们采用Barzilai-Borwein（BB）规则在每次迭代时线搜索步长进行初始化[9]，大大加快了收敛速度，选用了软阈值函数，使低分辨率图像去噪的同时原始信息丢失减少，因此迭代收缩阈值法[10-11]与传统算法相比，具有迭代时间短、重构的高分辨率图像质量高的优点。本文主要对迭代收缩阈值算法进行研究和介绍。

1 系统的构成与理论

1.1 FPM 的工作原理

傅里叶叠层成像的重构过程是指在成像平台下通过点亮不同位置的LED 对样本进行照射，经过物镜成像后再由CCD 进行低分辨率图像的采集，采集系统原理如图1所示。FPM 利用在空域和频域中的约束条件进行迭代来实现样本高分辨率图像的重建，整个流程详见图2[12]。

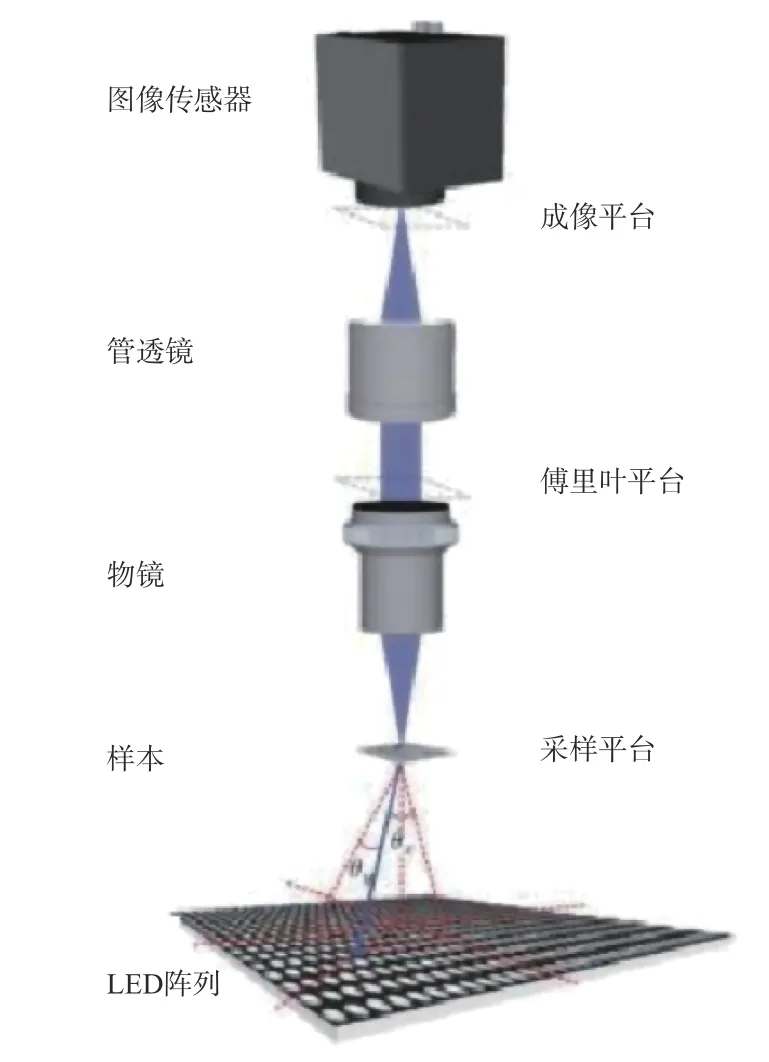
图1 傅里叶叠层显微成像系统原理图Fig.1 Schematic diagram of Fourier ptychographic microscopy system

该算法大致分为以下几步：

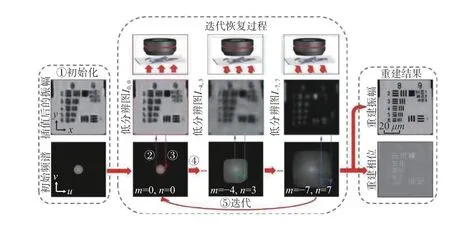
图2 傅里叶叠层成像算法迭代流程图Fig.2 Iterative flow chart of Fourier ptychographic microscopy algorithm

第2 步,从该频谱中选取一小部分区域，对选中部分的频谱做傅里叶变换，目标产生一个低分辨率的图片。如图2 中正常入射光对应第②步圆孔部分从而采集到的图片的频谱。

第3 步,在入射光的入射角度为i的情况下获取低分辨率图像，并测量出平方根。将目标图像的幅值部分替换为得到新的目标图片。然后，用新的目标图像替换其在高分辨率频域内所对应的区域。

第4 步,对于第i个区域，重复步骤2 和3。每块区域均有自己的低分辨率强度测量值相邻区域都必须有重叠部分。对所有的图片均重复上述迭代过程，直到所有高分辨率图像的频域部分均被低分辨率强度测量的数据更新过。

最后，重复步骤1～4，不同照明角度的N幅图像均被更新过后，直到达到高分辨率复振幅收敛的目标。

1.2 凸优化对低分辨率图像去噪原理

1.2.1 软阈值算子

凸优化模型中的局部极小值即最小值。常用的凸优化方法有固定点迭代法[13]、牛顿法[14]、梯度下降法[15]，本文将重点研究迭代阀值法，软阀值收缩算子Sτ(·)是算法的关键。

设矩阵x∈Rm×n，对任意给定的正数 τ，定义其中

对去噪前图像信号进行小波分解，设定一个阈值，对幅值大于阈值的小波系数进行保留，幅值小于阈值的小波系数置为零，从而恢复出有效信号，实现去噪处理。

1.2.2 迭代阈值算法（IST）

我们考虑解决以下一般性问题：

式中：l(w)是连续可微的；r(w)是一个非光滑非凸的连续函数；f(w)是从下面有界的。我们提出的一般迭代收缩和阈值化(IST)算法通过生成序列{w(k)}来解决公式（2）。

公式（3）等价于下面的近端算子问题：

因此，在IST 中，我们首先沿方向-∇l(w(k))执行步长为1/t(k)的梯度下降。其中：

a）步长初始化

初始化步骤大小采用Barzilai Borwein（BB）规则，其使用一个对角矩阵t(k)I近似黑塞矩阵∇2l(w)，当w=w(k)表示为

然后将t(k)在外迭代k处初始化为

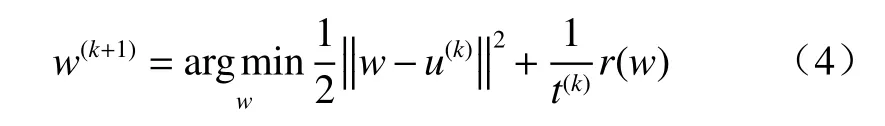
b）线搜索标准

线搜索准则是要求目标函数值单调递减，在外迭代k处满足以下单调行搜索条件：

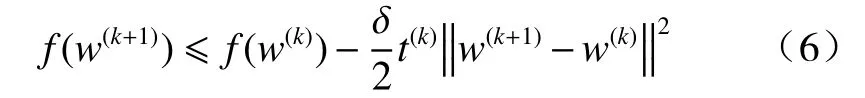
如果w(k+1)使目标函数值小于前面出现的最大m（m＞1），迭代如下：

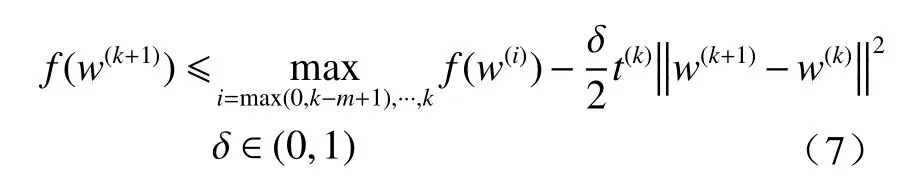
总结上述过程，我们可得到迭代阀值算法具体步骤如下：

1）选择参数η＞1 和tmin，tmax且0＜tmin＜tmax;

2）初始化迭代计数器k←0 和有界起点w(0)；

3）Repeat；

4）t(k)∈[tmin,tmax]；

5）Repeat；

7）t(k)←ηt(k)；

8）Until 满足线性搜索条件；

9）k←k+1；

10）Until 满足停止标准。

2 实验结果与分析

2.1 实验装置

图3 为实验硬件结构图。它主要由照明系统、图像成像系统和图像采集系统组成。照明系统由可编程LED 阵列、Arduino 控制器构成，LED为32×32 可编程LED 阵列，相邻LED 间距为4 mm。图像成像系统由放大倍数为4 倍、等效数值孔径NA为0.1 的物镜和195 mm 共轭的平场物镜（PH100系列生物显微镜）构成。图像采集系统由KUYNICEIUA2 0000KPA 工业数字相机和ImageView 软件等构成。

2.2 实验结果分析

首先，USAF 分辨率板到LED 平面的距离为98.8 mm，通过对Arduino 控制器进行编码控制LED 阵列，用中心区域的15×15 个LED 作为光源，LED 中心波长为625.4 nm，再由成像系统采集低分辨率图像，由ImageView 软件进行调参设置及图像保存。共采集225 张分辨率为440×440 pixels 图像，对采集的低分辨率图像做3 组对比试验：用采集的低分辨率图像原图和经凸优化处理、中值滤波处理后的低分辨率图像分别进行重构，得到高分辨率图像，傅里叶叠层成像技术对采集的原图进行重构得到高分辨率图像。图片处理和重构过程在Matlab2018b 上完成。实验结果如图4所示。

图4 实验结果图Fig.4 Diagram of experimental results

表1 为3 组实验所得图像的质量评价结果。由表中数据可以得知，中值滤波处理后的重构图像和低分辨率原图的重构图像PSNR 和SSIM 值十分相近，而凸优化处理后重构的图像的PSNR和SSIM 值明显更高，图像质量更高，且时间损耗并不大。从重建实验图片看，重建的结果还不是很好，造成此现象的原因是采集时点亮的LED 灯的数量会影响采集的低分辨率图像质量，从而影响重构高分辨率图像质量。在之后的实验里，我们将通过每次随机点亮1 个、4 个、8 个、16 个LED 来获取低分辨率图像，从而重建高分辨率图像，再通过图像质量评价标准对比得出了相对最优照明策略，提高重构高分辨率图像质量。

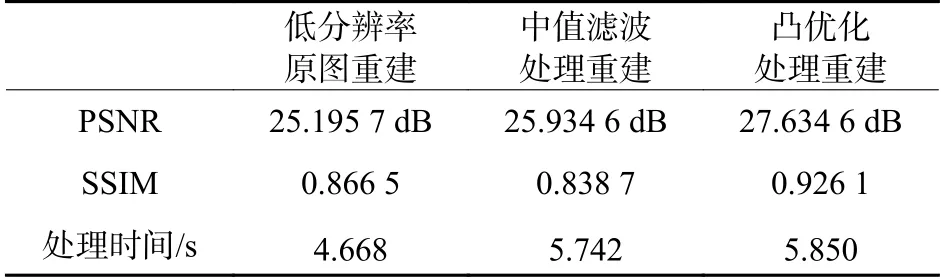
表1 重建图像质量评价结果Table 1 Quality evaluation results of reconstruction images

3 结论

本文根据FPM 中采集的大量低分辨率图像会直接影响高分辨率图像的重构质量，提出了对低分辨率图像进行凸优化处理，以达到重构图像质量提升的目的。文中着重介绍了凸优化相关理论和迭代阈值算法，并进行了3 组对比实验。实验结果表明：迭代收缩过程中采用了BB 规则，提高了迭代速度，并不会产生太多的时间损耗，且凸优化与传统的去噪方法相比会减少图像原始信息的丢失，重构出的图像PSNR、SSIM 为27.634 6 dB和0.926 1，处理时间为5.850 s，与另外2 组相比有了明显提升，因此基于凸优化的傅里叶叠层成像技术具有时间损耗不大的情况下提高重构图像质量的优点。