超大视场折反射全景光学成像系统设计
曹一青
(1.莆田学院 机电工程学院,福建 莆田 351100;2.福建省激光精密加工工程技术研究中心,福建 莆田 351100)
引言
随着社会经济和科学技术的不断发展,人们对图像信息采集的要求越来越高,传统成像设备的视场范围存在一定局限性。超大视场光学系统(如鱼眼镜头、折反射全景成像系统等)具有大视场角特点,能够避免常规光学系统拍摄大视场范围图像应用拼接法带来的原始数据量大、拼接算法复杂及实时性差等问题,因此被广泛应用于机器人导航、虚拟现实和运动目标检测等领域中[1-4]。相比于鱼眼镜头系统,折反射全景光学成像系统仅由1 块反射镜和1 组常规光学系统构成,结构相对简单[5]。目前,随着图像传感技术的不断发展,人们对折反射全景光学成像系统的像质提出了更高要求,使得此类系统的设计成为目前急需解决的问题。
折反射全景光学成像系统中光学元件虽然是轴对称布置,但是大视场物点发出的成像光束以较大的入射角(大于800)打在系统光学元件表面上,使得它具有平面对称光学系统的成像特性,导致简单地应用轴对称光学系统的像差理论很难解决此类系统的设计问题[6]。国内外研究人员对折反射全景光学成像系统设计进行了详细地探索,提出了许多系统设计方法[7-10],尤其是上海大学吕丽军基于三阶平面对称光学系统像差理论研究了此类系统的优化设计方法[6],但是该方法仅针对中小孔径成像情况。目前人们为了获得更清晰图像,往往追求大孔径成像,在这种情况下系统高阶像差贡献显著[11],导致在设计过程中缺少较完整的设计理论对其进行分析,以及缺少确定结构参数的方法。
鉴于上述问题,本文应用光焦度控制方程和超大视场光学系统六阶波像差理论研究了超大视场折反射全景光学成像系统结构参数初步确定方法,结合Zemax 软件设计了一款全视场角范围为12°~178°,F数为3.5,成像性能良好的系统,为以后设计超大视场折反射全景成像系统提供了一种有效的方法。
1 超大视场光学系统六阶波像差理论
折反射全景光学成像系统具有平面对称光学系统成像特性,本文应用超大视场光学系统六阶波像差理论对其进行像差分析[12]。反射和折射式超大视场光学系统光路图如图1所示。图1 中AiOiOi+1Oi+2为主光线,交第k(k=i,i+1)个光学面于 Ok,并交光轴于Mk-1;ωk-1为光线AiOiOi+1Oi+2在第k个光学面的视场角,αk、βk分别为主光线在第k个光学面的入射角和反射角或折射角,nk-1、nk分别为第k个光学面的物方和像方空间折射率;在第k个光学面上的点 Ok处的法线与光轴相交于 Ck,同时第k个光学面与光轴相交于 Dk;沿光轴方向光学面之间的距离为。

图1 含反射和折射式超大视场光学系统光路图Fig.1 Optical scheme of an ultra-wide angle optical system consisting of the cases of reflection and refraction
应用波像差理论计算系统波像差时,首先需要通过主光线传递方程计算各个光学面的入射角α和反射角或折射角 β,方程式如下:
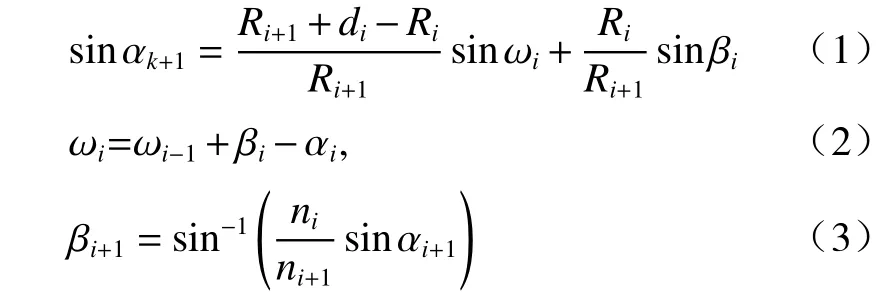
式中Rk为第k个光学面的曲率半径。
对于由g块光学面组成的光学系统,它的本征波像差计算表达式为

其中,
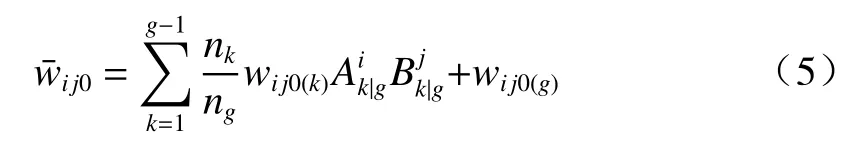
式中:xg,yg为第g块光学面的光瞳坐标;Ak|g,Bk|g是光瞳坐标在光学面之间线性传递系数,其表达式为

从上述分析可以得出,计算波像差需要首先知道光学面的物方、像方空间在子午和弧矢平面内的焦距它们可以应用二阶波像差系数w200=0和w020=0来确定[12]。
由于在大相对孔径和大视场角成像情况下,必须考虑衍生波像差和光瞳坐标二阶精度传递对波像差修正的贡献,因此在超大视场光学系统六阶波像差理论中系统总波像差系数计算表达式为
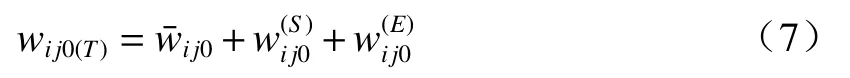
2 折反射全景光学成像系统设计
2.1 初始结构参数确定方法
系统初始结构选取是否合适至关重要,它直接影响着后续优化结果。因此,本文提出将折反射全景光学成像系统分为两部分,即前组和后组系统,然后应用系统光焦度控制方程和基于超大视场六阶波像差理论建立前后组系统波像差平衡方程,提出一种初步确定该类系统结构初始参数的方法。根据系统总光焦度、前组和后组系统光焦度的关系表达式(8),合理分配各部分透镜组光焦度:

式中:Φ前和Φ后分别为前组和后组系统光焦度,d前-后为它们之间的间隔。
应用高斯光学和矩阵光学理论[13-14]可得由g块透镜组成的系统矩阵为
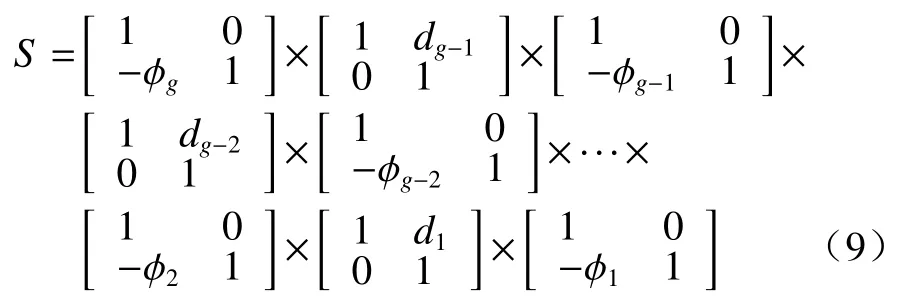
式中:ϕk(k=1,2,...g)表示第k块透镜的光焦度;dk为第k块与第k+1块透镜之间的间隔。
根据系统矩阵的性质和公式(9),可得到由g块透镜组成的系统等效光焦度方程:

由于系统结构设计参数较多,将最初始的前组系统结构作为已知条件,求解出后组系统结构参数来平衡前组系统像差,达到初步校正系统总像差的目的。另外,系统成像性能是针对整个视场角范围综合评价得到的,超大视场折反射全景成像系统视场角范围较广,所以选择具有代表性的0.707ω视场角作为研究对象。应用超大视场光学系统六阶波像差理论计算前、后组光学系统在该视场角情况下的三阶、五阶彗差波像差和四阶、六阶球差波像差,并以前组系统波像差为约束条件,建立波像差平衡表达式:
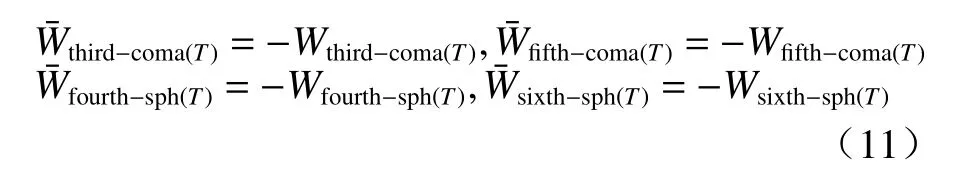
式中:Wthird-coma(T)、Wfifth-coma(T)和Wfourth-sph(T)、Wsixth-sph(T)分别为前组系统的三阶、五阶彗差波像差和四阶球差、六阶球差波像差;W¯区分于W,表示后组系统情况。
最后,结合光焦度控制理论方程及系统波像差平衡表达式,应用数值方法对它们进行求解,得到系统结构初始解。
2.2 设计实例
应用设计实例来详细讨论折反射全景光学成像系统设计方法。系统设计指标为:工作波段为可见光,全视场角范围为12°~178°,F数为3.5,焦距为2 mm 和总长小于130 mm。为了得到有利于系统优化的初始结构参数,首先需要在参考文献和专利数据库中并结合设计经验选取一个最初始结构,选择依据是折反射全景光学成像系统由反射镜和常规光学镜头系统组成,以及双高斯镜头光学结构能更有效校正像差的特点,本文设计系统的最初始结构从右向左依次为1 块球面反射镜和1 组具有双高斯镜头结构的透镜组(图2 中Lens1~Lens6),对应系统结构分布图如图2所示,光学参数由表1 给出。该光学系统中的反射镜和Lens1~Lens3、Lens4~Lens6 分别作为前组、后组系统。
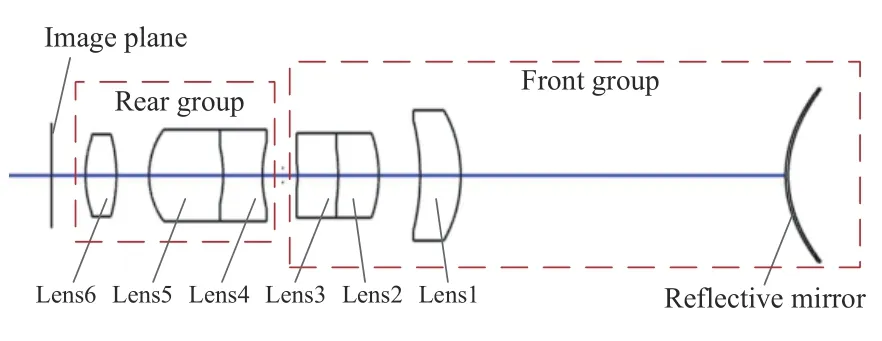
图2 折反射全景光学成像系统最初始结构分布图Fig.2 Primal structure distribution diagram of catadioptric panoramic optical imaging system
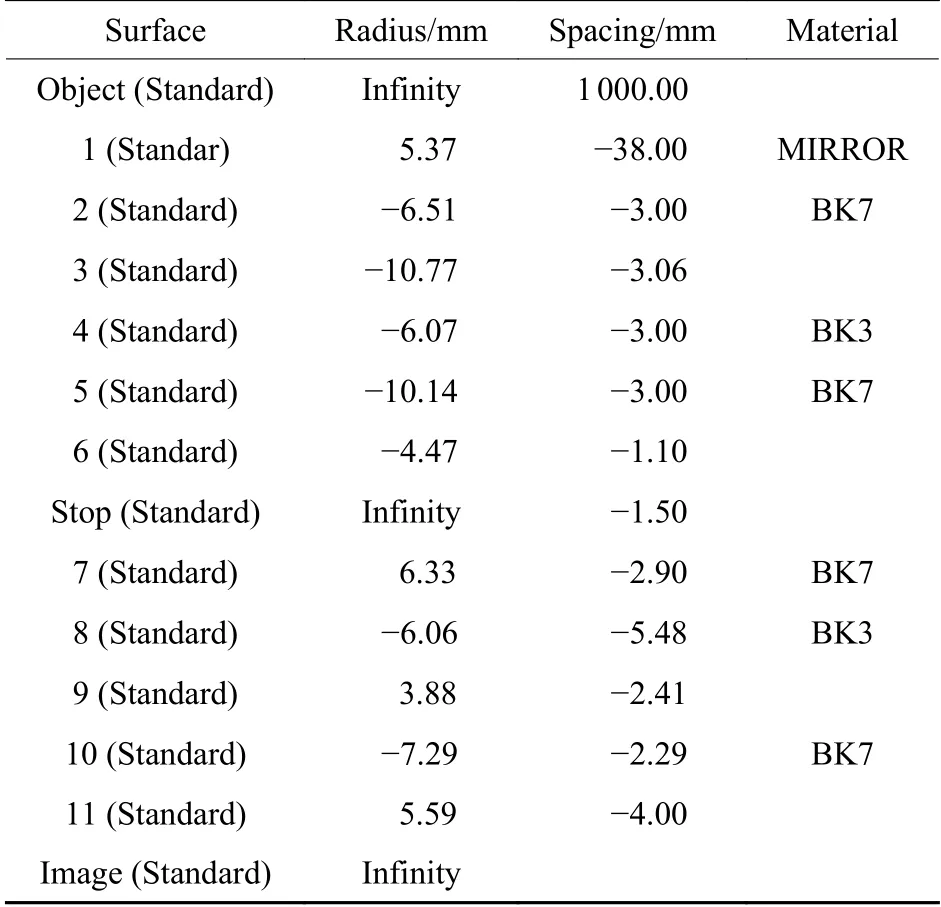
表1 折反射全景光学成像系统最初始结构参数Table 1 Primal structure parameters of catadioptric panoramic optical imaging system with ultra-wide field of view
在表1 给出的系统初始结构参数基础上,根据设计指标对其结构参数(焦距、F数及视场角等)进行相应缩放和修改,得到的系统成像性能非常差,因此需要应用上述方法初步确定系统结构参数。具体步骤为:首先,在保证系统总光焦度指标不变情况下,根据(8)式和(10)式建立后组系统光焦度控制方程;其次,应用(7)式计算系统在半视场角为57.5°时的波像差,并将其设定为约束条件,列出后组系统波像差表达式,然后建立系统像差平衡表达式;最后联立光焦度控制方程和波像差平衡表达式,通过数值求解方法得到系统初步结构参数。但是,光学系统结构参数较多,很难单纯地应用解析方法来求解出高成像质量的系统,并且在像差平衡表达式中仅考虑了彗差和球差,需要经过后续反复的像差校正和像差平衡来实现。在应用上述方法确定初始结构的基础上,将系统反射镜设计成偶次非球面,并应用Zemax 软件对该系统像差进行反复优化[15-17],优化后得到的系统光路图如图3所示。对应的光学结构参数如表2所示。偶次非球面反射镜的非球面系数可以表示为[18]
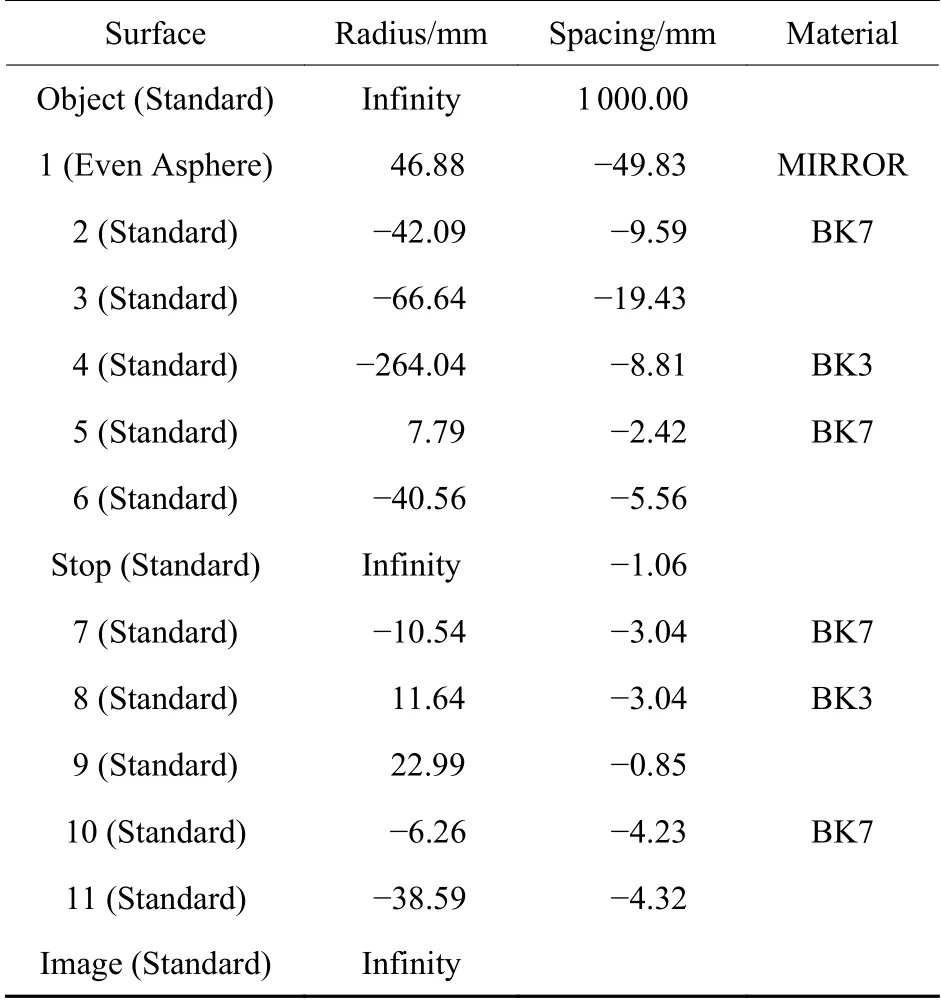
表2 优化后折反射全景光学成像系统光学结构参数Table 2 Optical structure parameters of optimized catadioptric panoramic optical imaging system
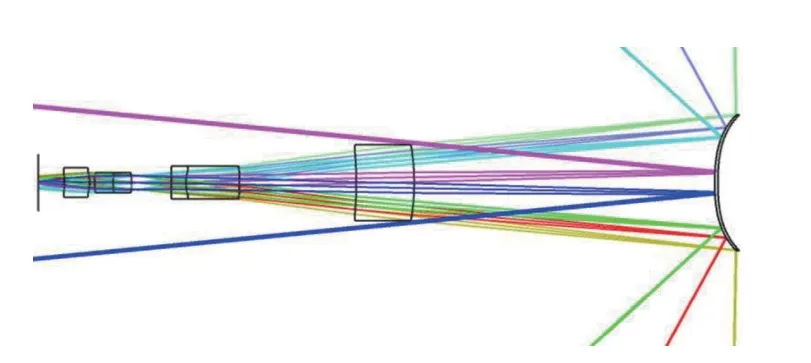
图3 优化后折反射全景成像光学系统光路图Fig.3 Optical scheme of optimized catadioptric omnidpanoramic optical imaging system
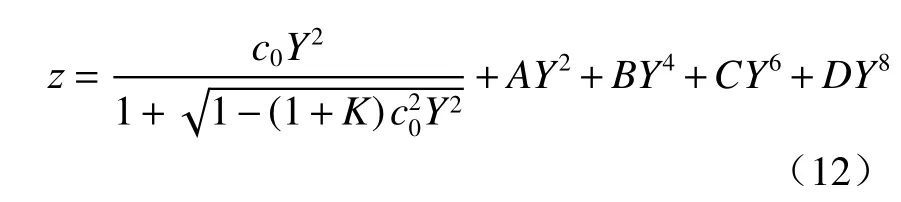
式中:c0=1/R0,R0为非球面顶点曲率半径;z和Y分别为非球面弧矢高度和弦高;K为非球面圆锥系数;A、B、C、D为非球面高次项系数。优化后折反射全景光学成像系统中偶次非球面反射镜非球面系数见表3所示。

表3 偶次非球面反射镜的非球面系数Table 3 Aspherical coefficients of even aspherical mirror
经过上述优化设计后,得到的折反射全景光学成像系统的调制传递函数(MTF)曲线如图4所示。从图4 中可以看出,系统在空间频率40 lp/mm 处,半视场角为6°,44.5°,62.9°和89°时子午和弧矢方向的MTF 值分别高于0.520 和0.583,0.376 和0.534,0.458 和0.613,0.480 和0.553,并且曲线平滑。此外,该系统在半视场角为6°,44.5°,62.9°和89°情况下的点列图如图5所示,对应均方根(RMS)半径由表4 给出,系统F-theta 畸变曲线如图6所示。由图6 可知,系统畸变在全视场角范围内均小于60%。因此,设计的系统具有较大相对孔径和大视场角范围,像差得到良好校正,成像质量较好。

图6 优化后折反射全景光学成像系统的畸变曲线Fig.6 Distortion curve of optimized catadioptric omnidpanoramic optical imaging system

表4 图5 中点列图对应的RMS 半径值Table 4 RMS radius of spot diagram shown as Fig.5
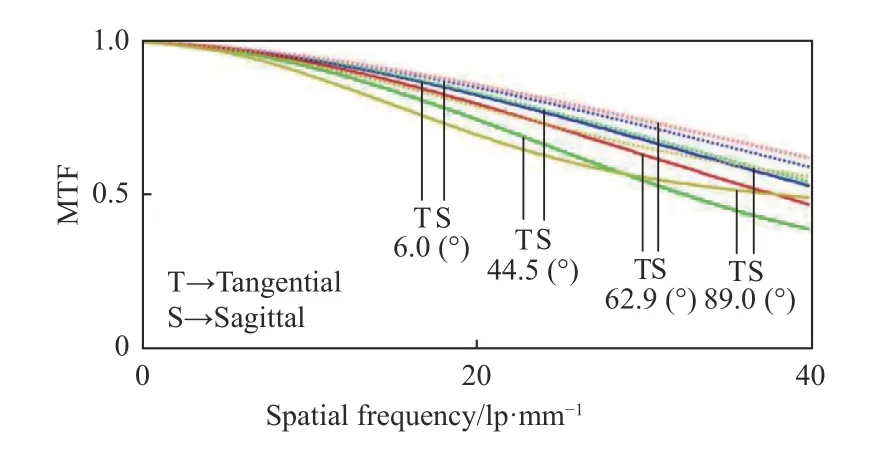
图4 优化后折反射全景光学成像系统MTF 曲线图Fig.4 MTF curves of optimized catadioptric panoramic optical imaging system

图5 优化后折反射全景光学成像系统点列图Fig.5 Spot diagram of optimized catadioptric panoramic optical imaging system
3 公差分析
通过优化设计得到了成像质量较好的折反射全景光学成像系统后,需要给系统中所有光学加工和装调分配公差。为保证系统能达到规定的性能指标,并考虑制造工艺和成本,本文应用Zemax软件对设计好的系统进行公差分析,得到较合适的公差范围。公差分析过程中,光学元件加工和装调误差分别设置为:1)表面公差,曲率半径为3 光圈、厚度为0.1 mm、X偏心和Y偏心均为0.05 mm、倾斜X轴和Y轴均为0.2°,S+A 不规则度为3 光圈;2)元件公差,X偏心和Y偏心均为0.05 mm、倾斜X轴和Y轴均为0.2°;3)折射率和阿贝数公差分别为0.001 和1%。采用系统半视场角在6°、44.5°、62.9°和89°情况下子午和弧矢方向的衍射MTF 的平均值作为评价函数,使用后焦补偿,在空间频率为40 lp/mm 处对系统进行400 次蒙特卡罗分析,具体分析结果见表5所示。由表5可知,系统具有较宽松的公差范围,便于后续加工和装调。
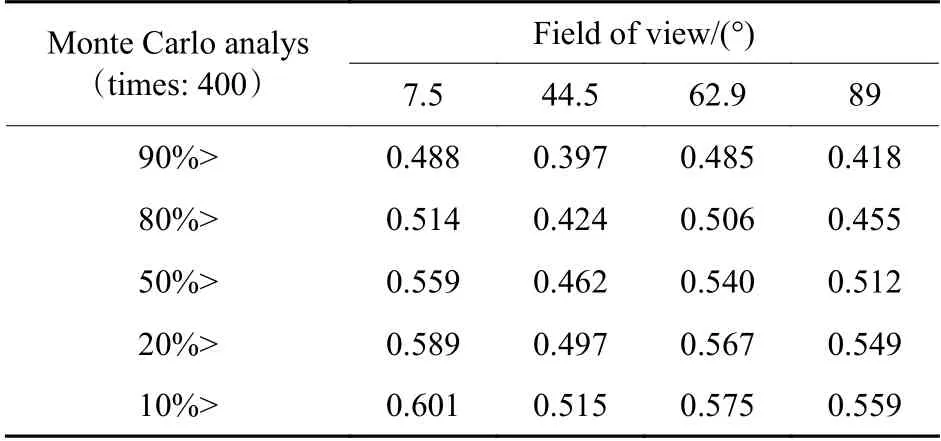
表5 优化折反射全景光学成像系统公差分析结果Table 5 Tolerance analysis results of optimized catadioptric panoramic optical imaging system
通过上述方法设计的折反射全景光学成像系统成像质量好,结构简单,且仅采用BK7 和BK3 两种较普通透镜材料,系统不仅满足实际应用要求,而且还能有效降低生产成本,具有较宽松的公差。
4 结论
由于目前折反射全景光学成像系统追求大相对孔径成像,本文结合光焦度控制方程,应用超大视场光学系统六阶波像差理论建立其像差平衡方程,初步对系统像差进行校正,获得较合适的初始结构参数。利用Zemax 软件对其进行优化设计,得到仅由1 片偶次非球面反射镜和6 片折射透镜组成的系统。该系统结构简单,视场角范围较广,F数为3.5,像差得到了有效校正,成像质量较好并具有较宽松的公差范围,能够满足实际应用要求。该类系统在安防监控、机器人导航及远程会议等领域均具有广阔的应用前景。

