光源角度对金属表面图像边缘的影响分析

甘 勇，于江豪，薛 菲，曾勃乔

（桂林电子科技大学 机电工程学院，广西 桂林 541004）

引言

随着图像处理技术的日益发展，从图像中直接获取所需要的特征数据技术也更加成熟。但是，图像成像质量的优劣直接影响着数据的可用性。为了获得更好的图像质量，就需要良好的图像采集系统，其中光源的状态直接影响着物件图像的相关特征。因此，在图像采集系统中稳定可靠的光源显得尤为重要。目前国内学者主要针对机器视觉系统光源的光斑以及发光强度对图像的影响开展了一系列研究，对于光源角度对图像的影响研究较少。王彦、王克逸、赵帅等人为了测量光线入射角度设计了一种锥形透镜，经过折射等变化得到图像光斑，测量精度高[1]。龚聪、徐杜针对光源强度对图像检测精度的影响做了分析研究，减小光源强度变化能够提高图像尺寸的测量精度[2]。龚志远等人提出了不同的光源角度对苹果糖度近红外光谱的影响，实验分析得到在45°时模型精度更高[3]。Regina Eckert，Zachary F.Phillips，Laura Waller 等人根据收集的数据和照明设置参数，在图像处理的基础上对明亮视野进行了照明角度的估计[4]。Jan Mescher，Adrian Mertens，Amos Egel 等人研究了典型的有机光电器件中光入射角度、吸收层厚度和光子捕获效率之间的相互依赖关系，光照的入射角度决定了吸收层的厚度[5]。郭静、冯鹏、邓露珍等人针对如何降低X 射线荧光CT 的康普顿散射噪声，模拟4 个角度下的射线投影数据，得到了有效的角度值[6]。马致臻、蒋上海、罗彬彬等人针对X 射线的探测角度对图像质量的影响，分析对比了3 种算法的成像质量效果，实验结果表明，优化探测角度结合合适的算法可以有效提升图像质量[7]。李通、赵巨峰、毛海锋等人研究了LED 角度优化对傅里叶显微成像的方法，得到了最佳的角度照明策略，证实了提出的策略有效[8]。程全、樊宇、刘玉春等人针对多个转动提之间的角度关系以及实时测量的需求，设计一种角度测量传感器，实现了该系统在角度测量方面的工程应用[9]。

综上所述，针对光源角度的变化，众多的研究学者皆是集中在照明角度对视野的影响或者对测量精度的影响展开较多的探讨，但是对于光源出射角度对图像边缘提取的分析研究较少。本文将主要对机器视觉系统中光源角度的变化对图像边缘提取的影响进行分析。

1 图像采集系统

机器视觉图像采集系统实验平台如图1所示。该系统主要由CMOS 采集相机、一套光源框架和灯组接口、4 组光照传感器、光源框架升降丝杆组、限位光电传感器以及计算机等部分组成。相机升降机构选用的是高精度滚珠丝杠，整个装置可以更广泛地适应不同焦距的镜头，也能够采集到更多不同状态下的图像。光源框架在升降丝杆的带动下可调节到不同的位置，使照射到工件表面上的光亮度有所不同，即改变图像的状态。试验工件为一个折弯4 次的钣金件，钣金件尺寸为155 mm×80 mm，工件模型如图2所示。钣金件上有2 个竖向和1 个横向的槽口，工件为3 mm 厚不锈钢材质，其中斜面的角度为120°。将工件放置于载物台的中央位置，调节相机和镜头焦距至合适的范围并锁定相机的高度。调节四面光源的初始亮度并保持一致，光照传感器将会实时返回当前光照值，光电传感器限制光源框架的运动范围，整个装置适应性更广泛，适合采集多种状态的图像。

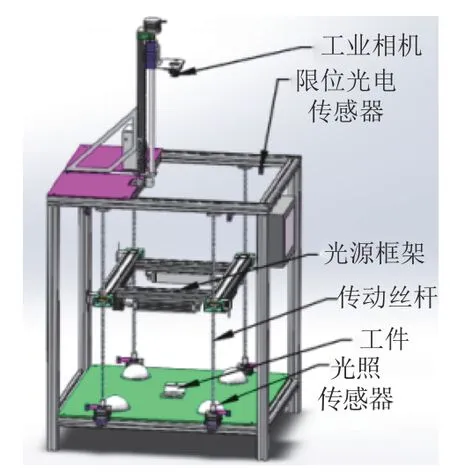
图1 图像采集系统Fig.1 Image acquisition system

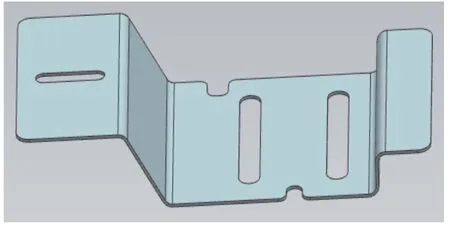
图2 工件模型Fig.2 Workpiece model

2 光源分析

2.1 光照理论依据及光源系统分析

针对不同的采集对象，选择合适的光源能够更有利于图像的采集。但是金属材质存在一种特殊属性，当光源照射到金属表面之后，在工件表面很容易产生高光现象，该现象仅通过调整相机光圈是无法彻底消除的。因此给图像采集工作带来较大困难，也会使采集的图像出现局部过亮现象，影响图像的特征输出。

金属表面产生高光的原因是由于次表面散射引起的，次表面散射现象是指光射入半透明物体后，光子在内部发生多次散射，部分光子又从金属表面的其他位置出射，并射入视野的光线传递的物理现象[10]。在金属表面的光线由于受到金属原子的影响，会有光子被吸收，少量的光线经过几次传递散射再次从表面射出，如果观察的视野大于光在金属内部的散射距离，那么就会从表面看到高光现象。

高光现象的产生和多个因素有关：一是材料本身，金属材料本身的粗糙度和制作形式会导致高光现象的产生；二是光源的角度，光源与物件表面垂直会增大高光现象产生的可能性；三是观察角度，沿着光线射入的角度观察相比于逆着射出光线观察更有可能看到高光现象。

对于光线在非透明物体表面发生的双向反射问题，有学者提出了用双向反射分布函数（BRDF）解释光线在非光学平面上发生的高亮现象，表征了入射方向和出射方向的辐射关系。BRDF 函数可表示为

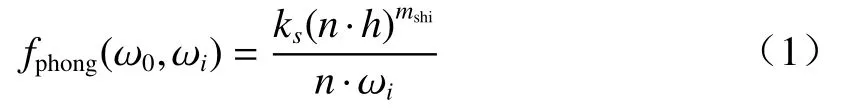
另外，光源的入射辐射率为

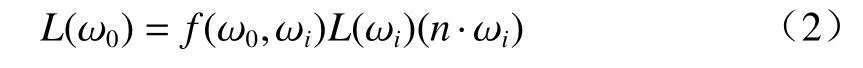
式中：f是BRDF 函数；ks是控制镜面反射的亮度；n·ωi是用于抵偿（2）式中的相应部分；L(ωi)是光源的入射辐射率（亮度）[11]。

在本次实验中采用适应性更广的四面可调光源，光源参数为LED 白光，色温6 500 K，光源辐照角度为32°，光源的机械可调节角度为90°。光源亮度通过光源控制器可以对4 通道的光源亮度进行调节。制作的工件为简单钣金件，由3 个平面和1 个斜面组成。3 个平面存在一定的高度差，则照射到其表面上的光线也会存在差异，根据光照的差异，可以对采集到的图像进行图像分割处理。

在本次试验中，所选用的材料为201 不锈钢，初始光源角度为四面垂直向下，采集相机位于光源中心正上方。通过建立光源角度和工件角度的关系模型（如图3所示），工件在光源照射角度内表面接收到的光线很少，并且在工件斜面上呈现无光（光线很少）状态。

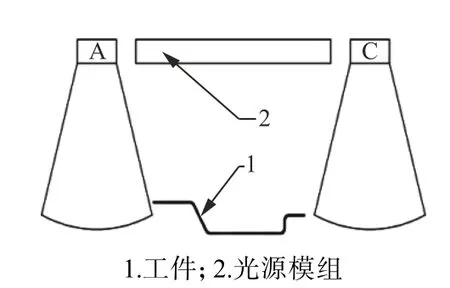
图3 光源-工件模型Fig.3 Light source-workpiece model

为了在工件周围形成良好的光斑，需要给工件均匀照明，在进行高度调节时应考虑光斑成形的大小，依据下式计算光源工作距离：

式中：L为光源光斑尺寸；dw为光源工作距离；DW是镜头工作距离；FOV为视野。

根据已知数据，工件的最大宽度为155 mm，视野范围FOV=352 mm，镜头焦距为35 mm，镜头的最小工作距离DW为500 mm，CMOS 相机的靶面尺寸为7.6 mm×5.7 mm。根据工件的最大外观尺寸以及如图4所示的像距和图像视野的关系，可以得到最小的物距为714 mm。在实际使用时，图像尺寸略大于工件尺寸，因此将工件尺寸设置为180 mm，可以得到物距距离约为DW=830 mm。

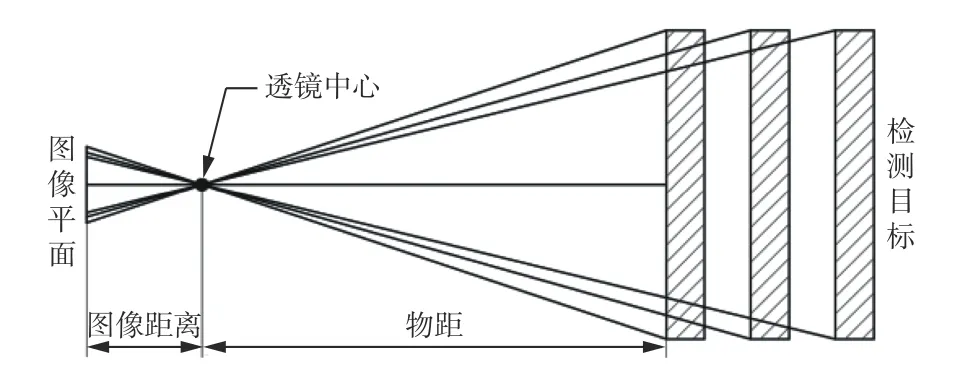
图4 像距和图像视野比例关系Fig.4 Relationship between image distance and image field of view ratio

镜头工作距离DW=830 mm，光斑范围大小为L= 452 mm，利用（3）式计算可得光源工作距离dw=235.80 mm。根据以上计算结果，调整光源到工件的距离。

2.2 光源角度影响分析

由光波叠加原理可知，同频率、同振动方向的单色光会产生叠加效果，其振动幅值是每一个到达该点的幅值的矢量和。同一点位的光照强度受到投射的所有独立光源的影响，如图5所示，同一点位受到多组光线的影响。

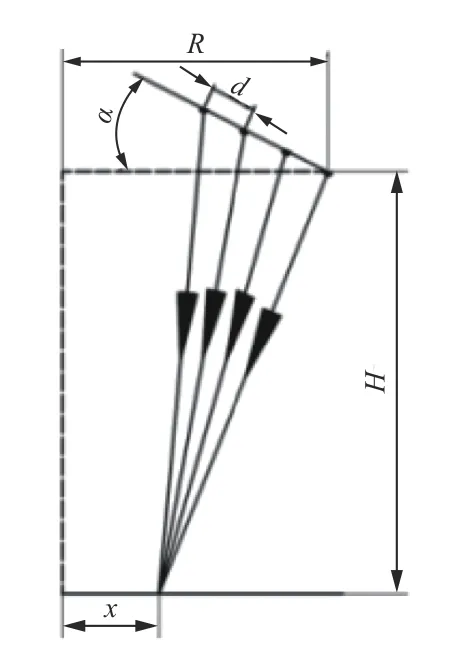
图5 光照投射示意图Fig.5 Schematic diagram of light projection

图5 中H为光源到被测物体的距离，R为光源半径，x为任意观测点，d为光源灯珠间隔，α为光源转动的角度[12]。

根据上述参数可确定光源转动的角度范围为

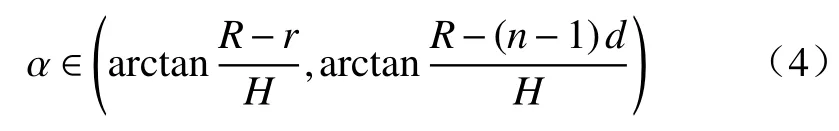
当角度旋转α时，H为

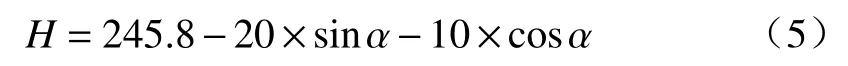
式中r为被测面半径。实际角度变化时，照射高度因为光源分布在不同层数的原因，照射距离发生差异，此时应对差异高度进行相对的误差补偿[13]。将光源进行分层光线叠加计算，在转动过程中，各层光源对点x处的光照度为

式中：I为单个灯具的光通量，本文中光源光通量是恒定的；R为灯珠到点x的距离；E为光照度。由图5 可以得到每层LED 灯珠到点x的距离为

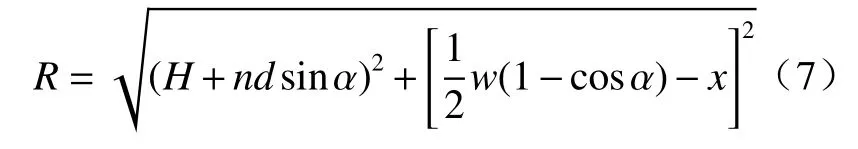
式中：w为灯带的宽度，w=40 mm；d为灯珠不同层之间的距离，d=4.5 mm。

将上述（5）～（7）式联立，可以得到m层灯珠到点x的光照度表达式：

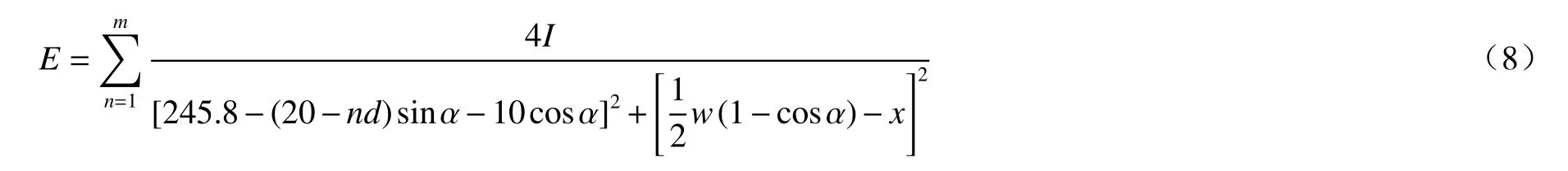
当α角度确定后，（8）式中的分母即为确定的值，只需要求出前半部分的最小值，也就是(20-nd)sinα+10cosα的最大值，利用求导法则可以得到α取值范围为[0°，90°]，进而可以求得α角度分别为57.17°、47.73°、33.02°、11.01°。在软件中模拟出上述角度下光照均匀性的平均偏差和标准偏差，如表1所示，曲线图如图6所示。

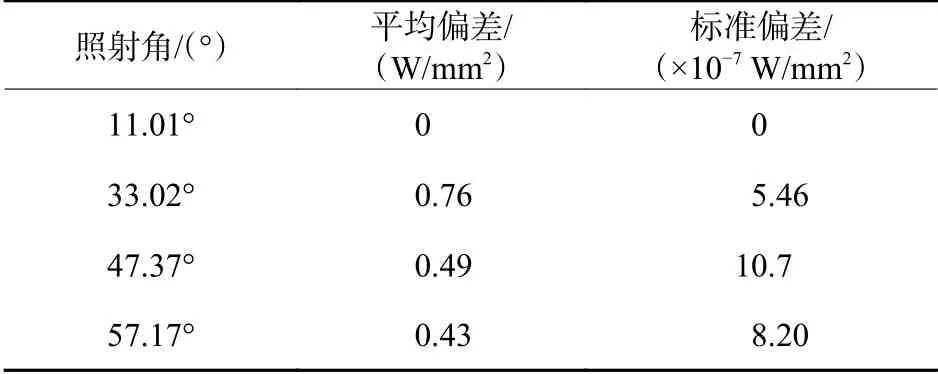
表1 光照均匀性平均偏差和标准偏差Table 1 Mean deviation and standard deviation of illumination uniformity

根据表1 和图6 可知，光源层数为4 层LED点光源，当光源照射角度为57.17°时，平均偏差和标准偏差是最合适的，表明在此角度下工件表面的光照均匀性最好。

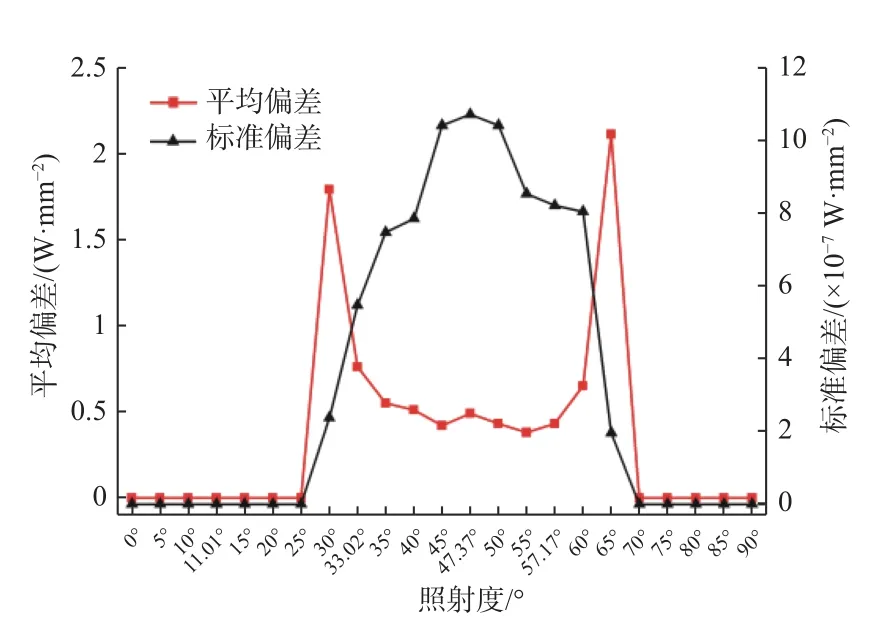
图6 角度与平均偏差、标准偏差的曲线图Fig.6 Curves of angle with mean deviation and standard deviation

3 实验验证

根据上述理论分析得到的结果，本实验将预先采取仿真实验进行分析。仿真软件是LightTools 8.4 版本，通过在该软件中建立光源仿真模型并依据前文设置相关参数。根据仿真结果调整实验平台，并进行实验验证。

3.1 仿真实验

通过模拟软件LightTools 建立光源三维模型，并将该软件和SolidWorks 软件之间的接口导入工件模型，设置相关参数模拟光源在工件表面上的分布情况。根据上述计算结果，工件到光源的高度距离为235.8 mm，修改高度设置并将工件的3 个平面和斜面作为光源光照的接收面。运行软件得到当前工件表面的光照情况，初始状态斜面上的仿真结果如图7所示。

依据图7 仿真结果可以看到，在设定高度235.8 mm，光源发光面面向载物台的状态下，工件的斜面上并未收到任何光照，此时从工业相机视野中看到的斜面图像与其他3 个面相比，接收到的光线更少。

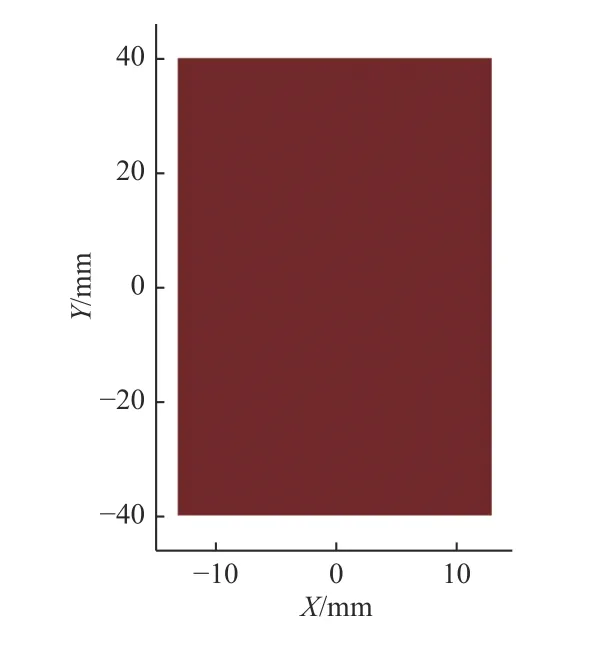
图7 高度235.8 mm 斜面仿真照度图Fig.7 Simulated illuminance diagram of inclined plane at 235.8 mm

在保持光源高度、光照强度不变的情况下，通过调整右侧光源的倾角，仿真得到不同角度下的光照分布数据（增加0°和90°作为对照数据），如图8所示。

根据图8 中6 组光照图像数据可知，高度和光照强度不变的情况下，在光源角度为57.17°时光照达到了较为理想的状态。

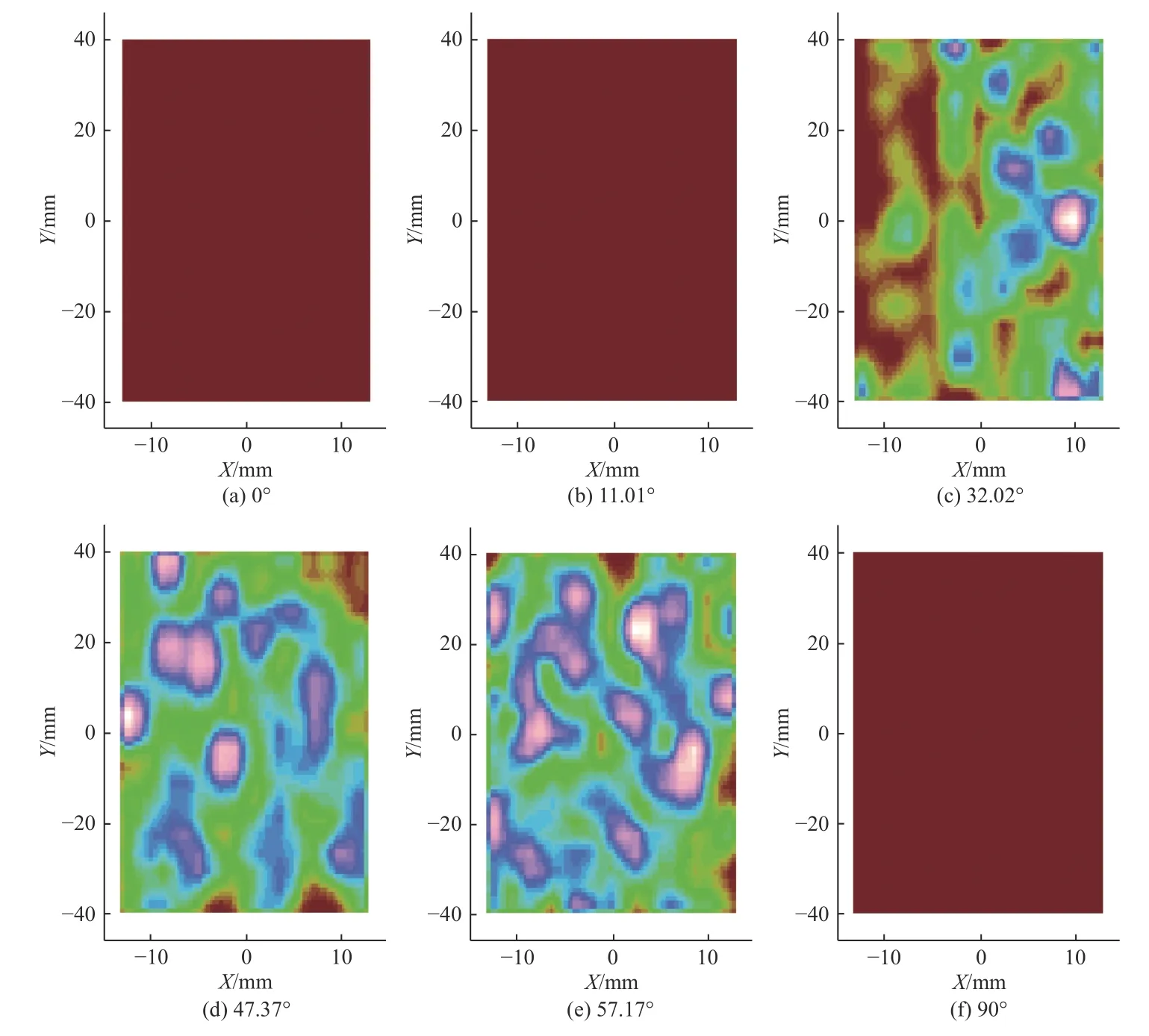
图8 高度235.8 mm 时不同光源角度工件光照分布Fig.8 Illumination distribution of workpieces with different light source angles at 235.8 mm

3.2 实验测试

依据上述结论，调节光源的机械角度为57.17°，将待测工件放置在视野场的中央位置，调节后的光源装置如图9所示。利用工业相机实际采集的图像如图10所示。

图9 调节后的装置相对位置图Fig.9 Relative position diagram of adjusted device

由图10 可以看出，通过改变光源照射角度，斜面上的光照有了明显的变化，在光源照射角度为57.17°时，整个工件表面的光照数据优于其他组。

图10 高度235.8 mm 时不同角度下的工件图像Fig.10 Images of workpieces at different angles at 235.8 mm

在Matlab 中获取的以上6 幅图像在水平方向时中间位置的光照曲线分布图如图11所示。

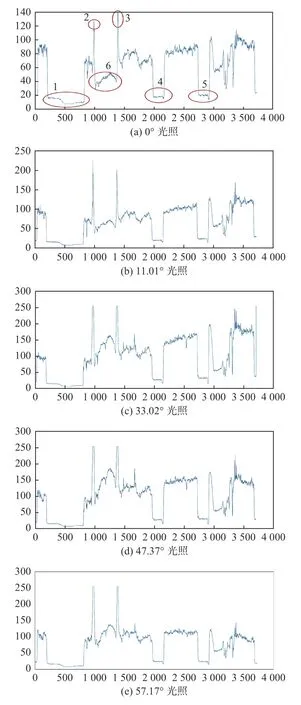
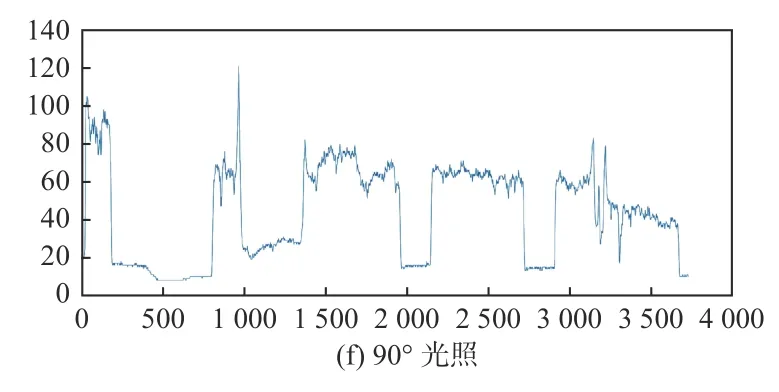
图11 Matlab 中6 幅图像中线处光照分布曲线Fig.11 Illumination distribution curves at midline of six images in Matlab

根据图11（a）可知，1号位置是水平方向的槽口，底色全部为黑色；2、3 号是2 个短凸起，其中间位置6 号就是斜面的位置；4、5 号表示的位置则是竖直方向的2 个槽口的位置。在整个图像的右端，光照数据产生较多的波动，其所在位置正是最后一个平面。对比其他的几个光照曲线图可看出，光源照射角度为0°和11.01°时，在斜面处出现2 个极值，90°时3 号极位消失，很容易在后续的数据处理中误判为异常数据点。综上所述，光源照射角度为57.17°时光照表现最好。

3.3 实验评价

边缘提取的目的是找到图像的最大外缘轮廓，将图像有效区域和无关背景分割开来，完整保留图像的重要特征属性。在进行图像边缘提取时，光照数据分布的均匀性直接影响了边缘图像的完整性。

本文采用单一变量法得到了均匀光照情况下灯带的角度是57.17°。在此基础上，通过使用sobel 边缘提取算法对上述57.17°和90°图像分别提取图像边缘进行直观的对比，验证光照角度的改变对边缘提取的影响。

Sobel 算法是利用水平和垂直方向的卷积核与图像的灰度值进行卷积运算，再将2 个方向的计算结果的平方和相加再开方运算，如（9）式所示的计算[14-15]，以此提取图像的边缘。Sobel 卷积核如图12所示。

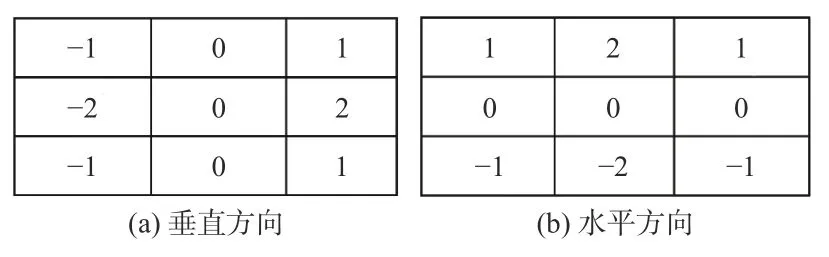
图12 Sobel 卷积核Fig.12 Sobel convolution kernel

式中：Gx代表垂直方向的卷积运算；Gy代表水平方向的卷积运算。

利用上述卷积核，与相应的图像进行卷积运算，得到原图的边缘图像。将57.17°的图像和90°光照下的图像分别进行数据处理，得到的边缘图像如图13 和图14所示。

图13 57.17°时的边缘图像Fig.13 Edge image at 57.17°

图14 90°时的边缘图像Fig.14 Edge image at 90°

从图13 和图14 可以看到，57.17°图像边缘提取效果明显优于90°的提取效果，57.17°的光照角度对于后续图像的处理也更加有利。利用边缘图像评价公式[16]：EIDx=ws×SSIM+wb×BIDx+wc×CIDx，计算得到图13 的EIDx是0.721 2，图14 的EIDx是0.677 9，这也反映出图13 的效果优于图14。

4 结论

通过模拟仿真和实验验证，并结合Matlab 分析图像的光照曲线图，将不同状态下的图像进行数据处理，得到了光源角度在57.17°时中线位置的光照数据，相比其他情况更为良好。利用Sobel 边缘提取算法得到了57.17°和90°情况下的边缘图像数据，表明57.17°下的图像轮廓清晰度更高而且更加完整，更加有利于图像分析，为机器视觉系统的光源照射优化提供了参考。