大尺寸太赫兹平顶波束的产生研究

邹开刚，刘 伟，肖 龙，项飞荻，沈思诗，杨振刚，刘劲松，王可嘉

（1.华中科技大学 武汉光电国家研究中心，湖北 武汉 430074；2.华中科技大学 光学与电子信息学院，湖北 武汉 430074；3.中国船舶重工集团公司第七〇一研究所 电磁兼容性重点实验室，湖北 武汉 430064）

引言

太赫兹波（terahertz，THz）是频率介于0.1 THz～10 THz 的电磁辐射。该领域研究起步较晚，随着近几十年来的太赫兹辐射源以及探测技术的发展，太赫兹波越来越多地被应用于安全检查，无损检测、无线通信、材料甄别、军事探测以及生物医学成像等领域[1-5]，其中成像技术的应用最为广泛。由于太赫兹波对于非金属非极性材料如陶瓷、脂肪、碳板、布料、塑料和复合物等具有良好的穿透性，可以利用其对样件进行无损检测成像，而且太赫兹波相比于毫米波检测成像而言分辨率更高；根据太赫兹波射线的低光子能量和对金属材料的强反射特性，还可以将其用于人体安检，且不会对人体产生电离损伤，同时如果结合太赫兹波的物质鉴别特性，还能够区分是否携带炸药或毒品[6-7]。

对于主动式成像系统来说，传统的聚焦高斯光源照明不仅效率低下，还会导致照明不均匀性，降低系统的成像信噪比，影响成像结果的可靠性。相比之下，横向光强均匀分布的平顶波束在很多场合下具有更好的成像效果，能够提供高信噪比[8]。目前已有多种平顶波束整形技术应用于可见光以及激光领域，如微透镜阵列整形、空间光调制器、衍射光学元件、自由曲面透镜整形等[9-12]。由于波长限制，基于相位的衍射光学元件整形技术，通过相位信息对光束进行整形，能够对较大波段范围的波束整形都有较好的效果。Gerchberg Saxton（G-S）迭代算法就是一种经典的设计衍射光学元件的算法，近几年来已有一些利用其改进算法对太赫兹波段进行平顶波束整形的研究[13-16]。2010年，Roman Kleindienst 等人基于该算法将625 GHz的高斯波束整形为发散的平顶波束，虽然是基于衍射理论设计，但是采用的是加工精度更好的折射型器件[17]；2017年，马学等人也利用G-S 算法实现了将2.52 THz 的高斯波束整形为直径11 mm 的环形波束[18]；2018年，Ye Xi 等人设计双衍射型相位透镜成功产生了直径40 mm 的可稳定传输的300 GHz 平顶波束[19]。现有的这些研究虽能成功产生太赫兹平顶波束，但是对于大尺寸的应用场景还是无法提供足够稳定的照明效率，这种针对能稳定传输的大尺寸太赫兹平顶波束的研究更是寥寥无几。

为弥补现有研究内容空缺，本文利用改进的G-S 算法——Input-Output（I-O）算法，设计了一个将太赫兹高斯波束整形为能稳定传输百毫米尺寸平顶波束的双相位板系统。该系统采用折射型加衍射型相位板组合系统，通过数值仿真检测系统的正确性，然后还搭建实验进一步验证了系统的实际有效性。该设计方法步骤简洁，且实验效果较优，能够为大尺寸太赫兹平顶波束研究提供一种有效的设计思路。

1 理论设计

本文采用双相位板结构设计整形系统，预设输出直径为200 mm 的大尺寸太赫兹平顶波束，设计原理如图1所示。

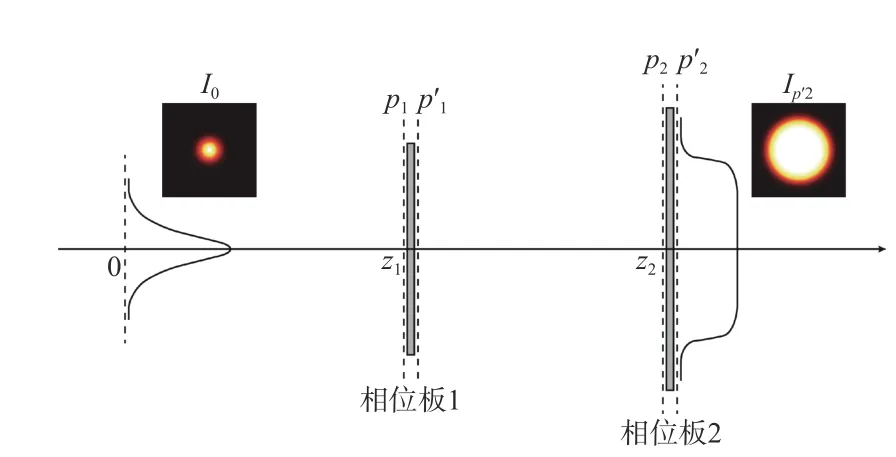
图1 平顶波束系统设计原理图Fig.1 Schematic diagram of flat-topped beam system design

输入为高斯光束，束腰处归一化强度为

式中 ω为束腰半径。设定束腰处z=0，相位板1 的坐标为z1，忽略其厚度，2 个表面分别用p1和表示；相位板2 同理，坐标为z2，2 个表面分别为p2、。面后即为目标平顶波束的光强分布，表征平顶波束光强分布的函数有多种，如超高斯函数、平顶高斯函数、超洛伦兹函数、平顶洛伦兹函数等，实际上这几种平顶函数轮廓相差并不大[20]，这里我们选取形式最为简洁的平顶洛伦兹函数作为预设的出射波束光强分布：

式中：q为阶数，q越大，平顶光斑边缘处越锐化；RFL即为预设平顶波束截面半径，这里取100 mm。

根据已知的输出光场，p1和处的光强与相位信息均可直接计算得到，根据薄透镜近似原理，相位板前后表面处的强度分布可认为一致，为求解双相位板厚度参数，需恢复和p2面处的相位信息，从而根据相位差得到相位板的厚度分布。GS 迭代算法就是一种典型的相位恢复算法，通过已知强度分布来求解满足精度的恢复相位。由于传统G-S 算法的收敛速度太慢，这里我们根据改进的G-S 算法（即I-O 算法）来提高迭代速度[21]，其原理框图如图2所示。

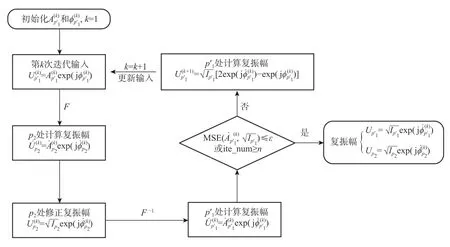
图2 Input-Output 算法流程图Fig.2 Flow chart of Input-Output algorithm

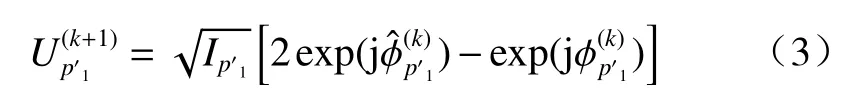
表1 双相位板系统设计参数Table 1 Design parameters of dual-phase plates system

考虑到后续实验中实际的波束变换需要一段过渡距离，如果2 块相位板间距太小，预期实验效果会较差，但是由于能量传输损耗，间距不可设置过大，故本设计中将间距参数设置为200 mm。于是得到2 块相位板4 个表面处的相位分布如图3所示。

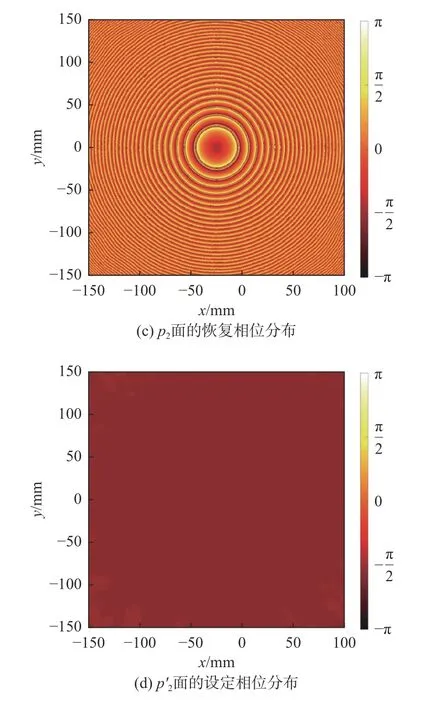
图3 相位分布图Fig.3 Diagram of phase distribution

2 仿真计算与分析

结合表1 的系统设计参数，理论输出结果如图4（a）所示。基于图3所示的相位恢复结果对系统进行数值仿真，仿真精度设置为0.2 mm，分别在z=846 mm 和z=946 mm 处计算仿真光强分布，结果如图4（b）与图4（c）所示。可以看出，光斑基本均匀，分析波束中心线处的横向轮廓（图4（d）），由于数值仿真具有一定的理想化条件，未考虑相位板本身厚度带来的影响，故仿真与理论结果相差不大。不过由于I-O 迭代算法恢复的相位是一种近似值，仍然存在迭代计算误差，所以与理论结果对比，2 个位置处的仿真结果都存在不同程度的波动偏差，尤其是平顶区域边缘处的光晕更为扩散。

图4 仿真结果Fig.4 Simulation results

为进一步评估结果的可靠度，我们分析计算平顶区域的2 个重要特征参数[22]——能量占比η和相对均方根。能量占比η可由（4）式计算：

式中I(r)为归一化强度。相对均方根URMS可由（5）式计算：

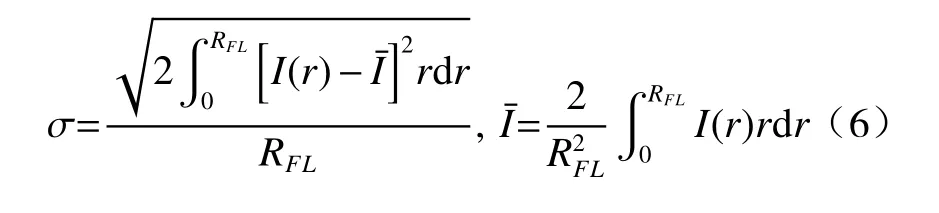
2 个参数均处于0～1 之间，能量占比越高，说明波束的整形效率高，能量泄漏情况很少，相对均方根URMS越高，说明波束的整形效果好，平顶区域更为均匀。以预设参数中的直径200 mm 圆形区域为平顶区域，理论与仿真结果中的能量占比η分别为89.14%、88.24%和87.77%，相对均方根URMS分别为0.698 4、0.787 2、0.775 6。可以看出由于迭代误差的存在导致仿真中平顶区域边缘处的光强差距更小，相对均方根要比理论结果更好。这是由于100 mm 的平顶半径是理论结果的初始设定，由于仿真中边缘更为平滑，仍然按照100 mm的半径计算会略小于仿真结果中实际的平顶半径。因此计算区域中的光强标准差更小，平均光强更大，故相对均方根也就偏大，不过相对差距在13%以内，可以判定仿真结果与理论在合理范围内吻合，验证了设计方法的正确性。

3 实验验证与分析

根据相位板前后表面的相位差计算得到厚度分布分别如图5（a）和图5（c）所示。

忽略厚度本身的损耗等影响，增减2π 的整数倍光程对应厚度不改变相位板的相位性能，考虑到实际中相位板材料的损耗，对厚度过大的相位板2 选用相位折叠后的衍射型厚度结构，如图5（d）所示。于是根据厚度结构计算结果得到2 个相位板三维模型分别如图5（b）和图5（e）所示，直径分别为140 mm 和270 mm。

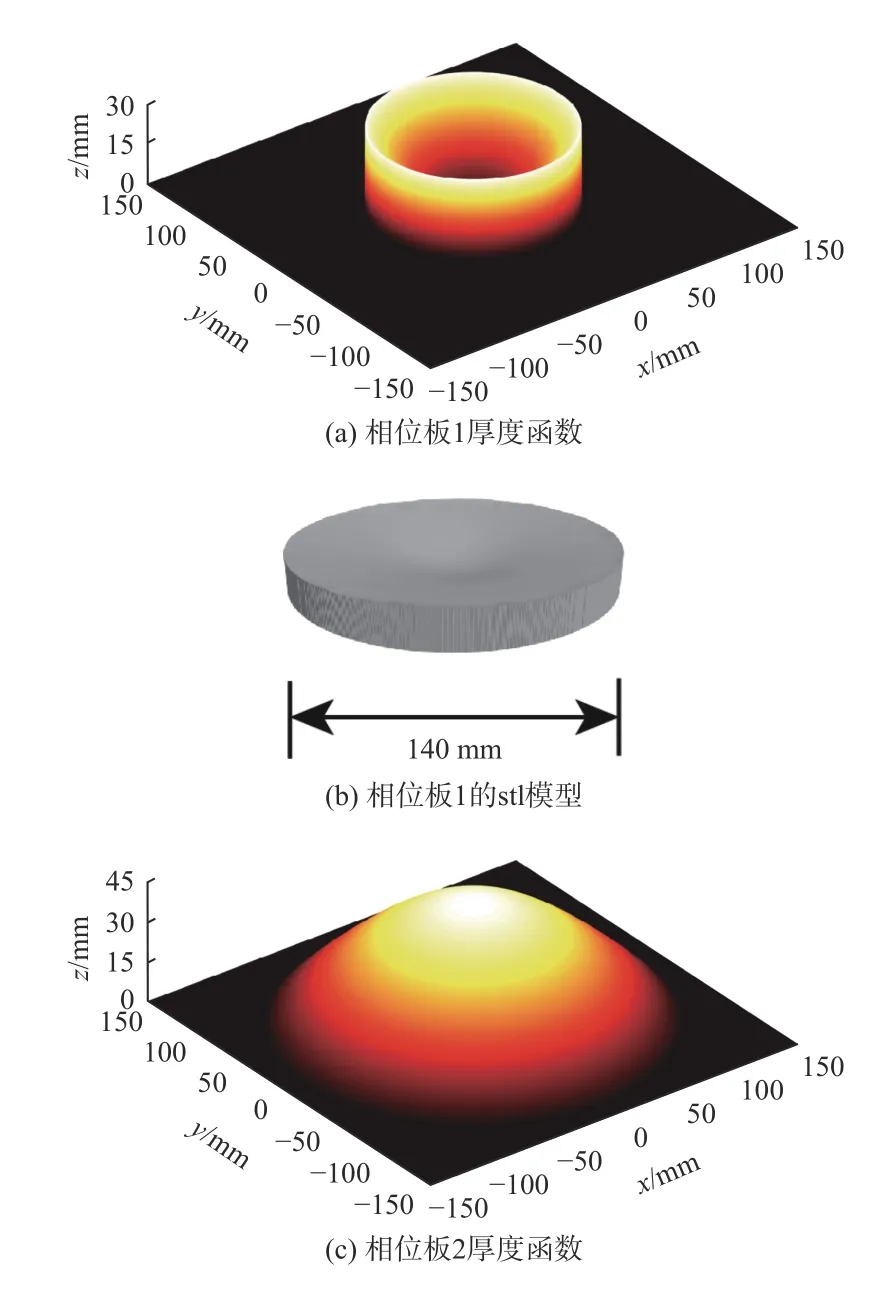
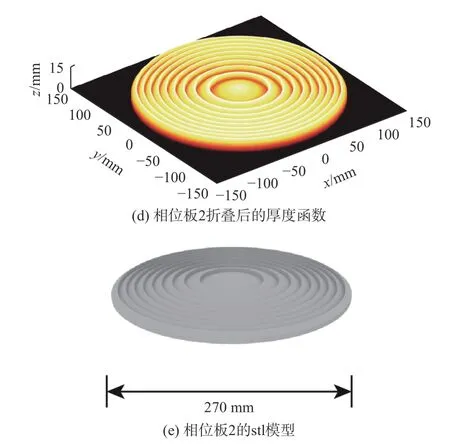
图5 相位板厚度函数及模型Fig.5 Thickness functions and models of phase plates

利用联泰科技公司型号为Lite450 的3D 打印机打印2 块相位板，成型误差在100 μm 以内，而本实验中源出射太赫兹波波长达3 mm，故相位板的成型误差对于实验结果影响很小，可以忽略不计。相位板1 的直径为140 mm，最大厚度为15.53 mm，相位板2 直径为270 mm，最大厚度为9 mm。根据设计的系统结构图搭建实验系统，如图6所示。

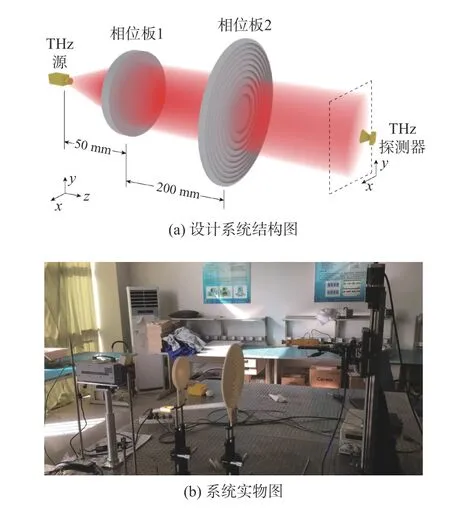
图6 设计整形系统图Fig.6 Diagram of designed shaping system

利用82406A 毫米波倍频源模块，输出频率为100 GHz 的太赫兹高斯波束，输出功率超过10 mW，探测器为肖特基二极管探测器，其工作的频段为75 GHz ～110 GHz，承受的功率在100 mW 范围内，具有皮秒量级的响应速度。拟合束腰位置位于源后146 mm 处，探测源出射光场如图7（a）所示。出射光斑拟合直径为59.71 mm，相位板1 与源间距50 mm，相位板2 与相位板1 间距200 mm，在与仿真一致的位置探测截面光场，结果分别如图7（b）和图7（c）所示。

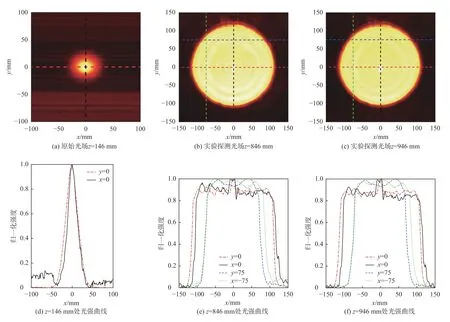
图7 实验结果图Fig.7 Diagram of experimental results

分别截取不同位置光强曲线进行对比分析（图7（d）～（f）），可以看出所设计系统在实验上成功将高斯波束整形为质量较好的平顶波束，实验结果中的平顶区域直径为228 mm，我们推测这是由于实际相位板存在损耗，平顶区域光强整体降低，其真实半高全宽比理论与仿真更大，故平顶区域直径也越大，不过与预设的截面光场直径相对误差为14%，在合理范围内。对理论、仿真以及实验结果统一参照（4）式～（6）式来进一步计算其特征参数，结果如表2所示。

表2 不同结果的平顶区域分析Table 2 Analysis of flat-topped region with different results

相比于理论和仿真，实验中由于能量损耗以及泄漏都受实际元器件影响，平顶区域光强被压低，边缘处光强差异缩小，其能量泄漏更为严重，故能量占比显著低于理论与仿真值；但是实际平顶区域光强标准差和平均光强之比更小了，故相对均方根越大，这正是产生大尺寸平顶波束需要的特点。

4 结论

本文基于相位恢复算法设计了一种大尺寸太赫兹平顶波束整形系统，实现了将高斯波束整形为大尺寸平顶波束，在设计基础上还进行了数值仿真，搭建了完整的波束整形实验系统，成功将束腰半径为6 mm 的高斯波束整形为直径d=228 mm的平顶波束，边缘清晰，可稳定传输，在至少100 mm的间距内光场几乎无差别，且相对均方根可达到89%以上。不过本实验中存在较明显的能量损耗，未来可利用不同材料以及调整设计参数进一步分析影响整形效果的因素，提高波束整形效果。

太赫兹波的相关研究起步较晚，其在成像应用领域具有的巨大潜在价值尚未被开发，很大一部分原因是受硬件技术限制，现有太赫兹源绝大部分都是高斯波源，不论是成像质量还是速度都存在较大不足。大尺寸太赫兹平顶波束能够突破现有太赫兹波成像的应用限制，提升成像速度以及质量，在无损检测、人体安检、材料甄别等领域都能显著提升太赫兹波的实用价值，进一步促进太赫兹波技术的发展。