异性截面钢拱桥整体-局部稳定性研究
张志程, 徐 韬, 王家豪
(湖南省交通科学研究院有限公司, 湖南 长沙 410015)
0 引言
传统拱桥一般为钢筋混凝土结构,随着我国桥梁建设技术发展,钢结构在拱桥建设中逐渐普及,钢结构的应用可有效增大拱桥的跨越能力,但钢结构的稳定性问题值得我们关注,特别是薄壁钢箱梁截面的钢拱桥[1-2]。以某大跨径异形截面钢拱桥为工程背景,建立该桥混合有限元模型,分析其线弹性阶段整体及局部稳定性,并与梁单元模型进行对比。研究成果可为异性截面拱桥动力分析提供参考。
1 工程概况
某大跨径钢结构拱桥,结构形式为中承式异性截面箱型拱,主桥跨径布置为(100+450+100)m,设计荷载为城-A级。边中跨拱肋位于同一平面内,倾斜度为0.2,主梁采用闭口薄壁箱梁截面,拱肋分为上、下两肢,边跨下肢拱采用二次抛物线,净矢高为4.5 m;主跨下肢拱采用悬链线,矢跨比1/5,拱轴系数为1.6。全桥共有吊杆38对,沿桥梁中轴线对称布置,地下结构为群桩基础。桥型布置见图1。
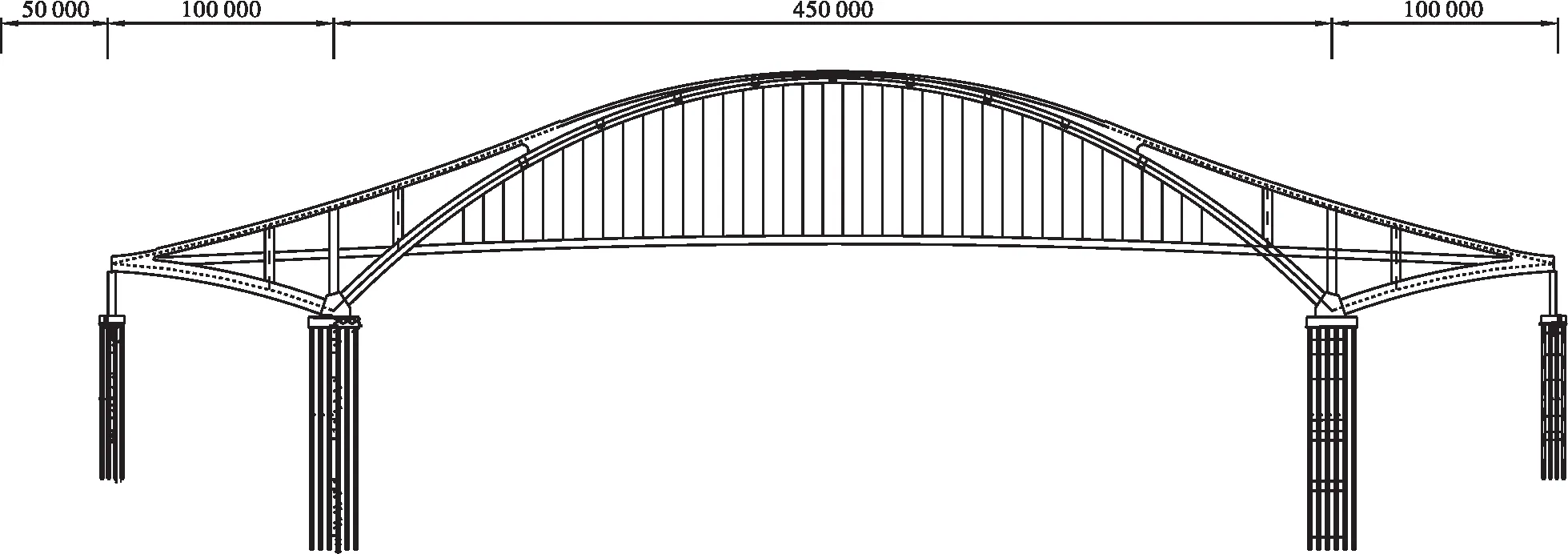
图1 桥型立面布置图(单位:mm)
2 有限元模型建立
对于薄壁形式的桥梁结构,全部使用梁单元很难精确反映结构的横向受力状态,而全部使用实体单元或者板壳单元则模型过于庞大,故本文拟采用混合单元法分析其线弹性稳定性[3]。混合有限元模型可有效避免局部分析中边界条件施加困难问题,是一种占用计算资源少、计算方便的有限元技术手段。
建立该桥梁-杆-壳混合有限元模型,其中拱肋采用Beam188梁单元建模,在拱顶位置嵌入一段30 m长的Shell63壳单元模型,梁单元与壳单元之间建立运动协调方程实现力与位移的平稳传递,吊杆单元使用Link10杆单元模拟,边墩与拱肋的支座通过弹簧单元模拟,主墩与边墩底部使用固结约束,主梁两侧压重使用Mass21质量单元模拟。有限元模型见图2。
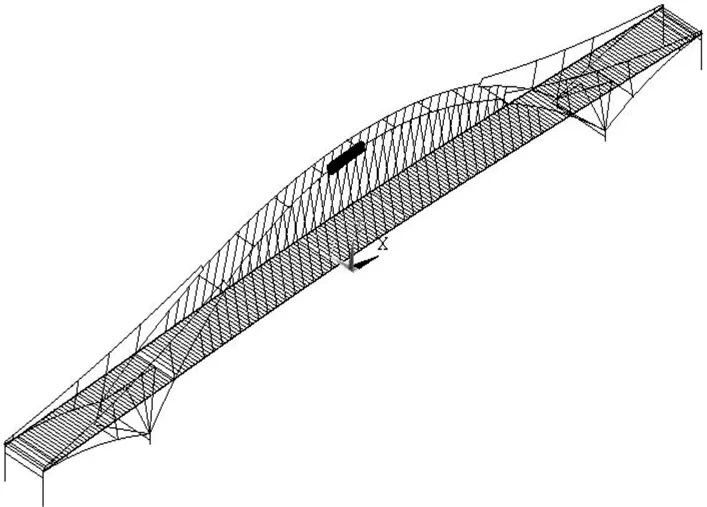
图2 有限元模型示意图
3 稳定性计算结果
对于拱桥而言,目前研究的重点都放在拱桥的整体稳定上,或者对单个构件的稳定问题进行研究,而针对大跨度钢拱桥整体-局部相关稳定问题的研究却很少。在实际工程中,由于大跨度钢拱桥的长细比较大,受力体系为偏心受压,再加上施工时可能产生的初始缺陷,很有可能出现整体-局部相关稳定问题[4]。因此对大跨度钢拱桥的整体-局部稳定问题进行研究非常必要。通过板壳有限元模型可以考虑箱梁截面畸变等局部变形,以期获得更为精确的稳定性系数解。本文选取以下计算工况,并按照规范进行荷载组合。同时,选用Beam188梁单元模拟全部拱肋结构作为对比模型,分析2种模型在相同荷载工况下稳定性系数区别。
工况情况。①工况1:恒载;②工况2:1.2恒载+1.4活载;③工况3:1.2恒载+1.4活载+1.0风荷载。
分别采用梁单元模型与混合单元模型进行工况1弹性稳定分析,具体结果见表1所示。计算结果表明:同一工况下2种不同模型前5阶屈曲系数近乎相同,且振型模态也相同,采用梁单元模型第6阶弹性屈曲系数为17.04,混合单元模型第6阶频率为15.12,较梁单元模型下降了11.3%。2种模态也不尽相同,梁单元模型模态为一阶拱肋平面内弯曲,其本质仍然属于整体失稳范畴;混合模型模态为中板加劲肋屈曲,属于局部失稳。
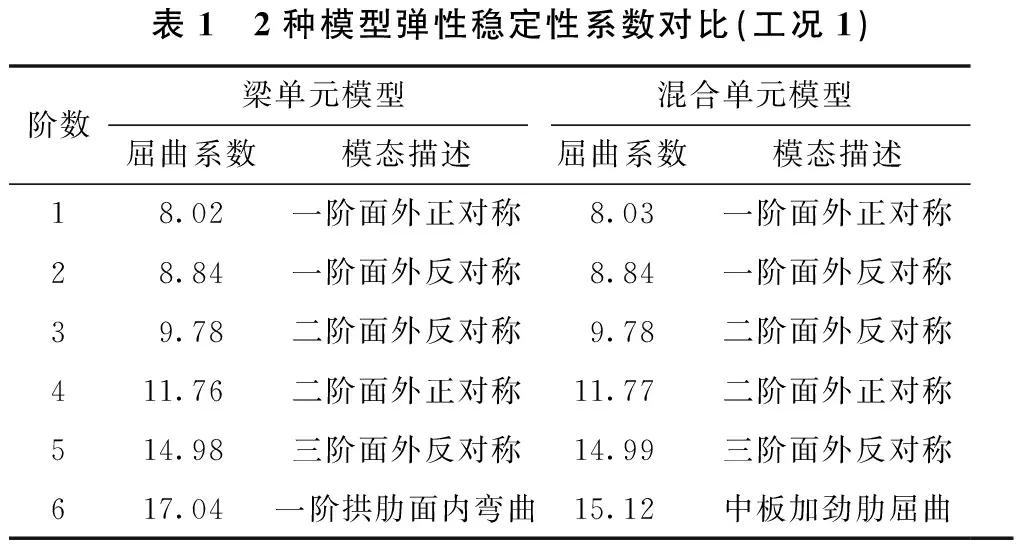
表1 2种模型弹性稳定性系数对比(工况1)阶数梁单元模型混合单元模型屈曲系数模态描述屈曲系数模态描述18.02一阶面外正对称8.03一阶面外正对称28.84一阶面外反对称8.84一阶面外反对称39.78二阶面外反对称9.78二阶面外反对称411.76二阶面外正对称11.77二阶面外正对称514.98三阶面外反对称14.99三阶面外反对称617.04一阶拱肋面内弯曲15.12中板加劲肋屈曲
分别采用梁单元模型与混合单元模型进行工况2弹性稳定分析,具体结果见表2所示。计算结果表明:同一工况下2种模型前4阶屈曲系数近乎相同,且振型模态也相同,从第5阶模态起,梁单元模型仍然为整体失稳,与工况1相同;但混合有限元模型5~6阶模态均为局部加劲板失稳,屈曲系数相比梁单元模型更小,屈曲系数分别降低3.3%、9.48%。
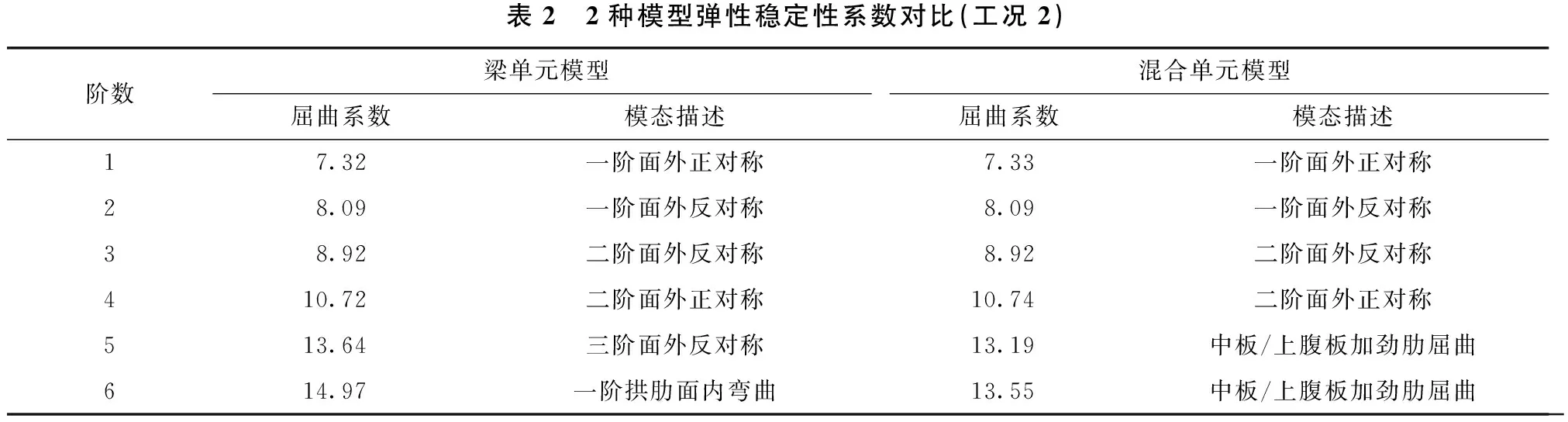
表2 2种模型弹性稳定性系数对比(工况2)阶数梁单元模型混合单元模型屈曲系数模态描述屈曲系数模态描述17.32一阶面外正对称7.33一阶面外正对称28.09一阶面外反对称8.09一阶面外反对称38.92二阶面外反对称8.92二阶面外反对称410.72二阶面外正对称10.74二阶面外正对称513.64三阶面外反对称13.19中板/上腹板加劲肋屈曲614.97一阶拱肋面内弯曲13.55中板/上腹板加劲肋屈曲
分别采用梁单元模型与混合单元模型进行工况3弹性稳定分析,具体结果见表3所示。计算结果表明:同一工况下2种模型前4阶屈曲系数近乎相同,且振型模态也相同,从第5阶模态起,梁单元模型仍然为整体失稳,与工况1相同;但混合有限元模型5~6阶模态均为局部加劲板失稳,屈曲系数相比梁单元模型更小,屈曲系数分别降低3.25%、9.45%。
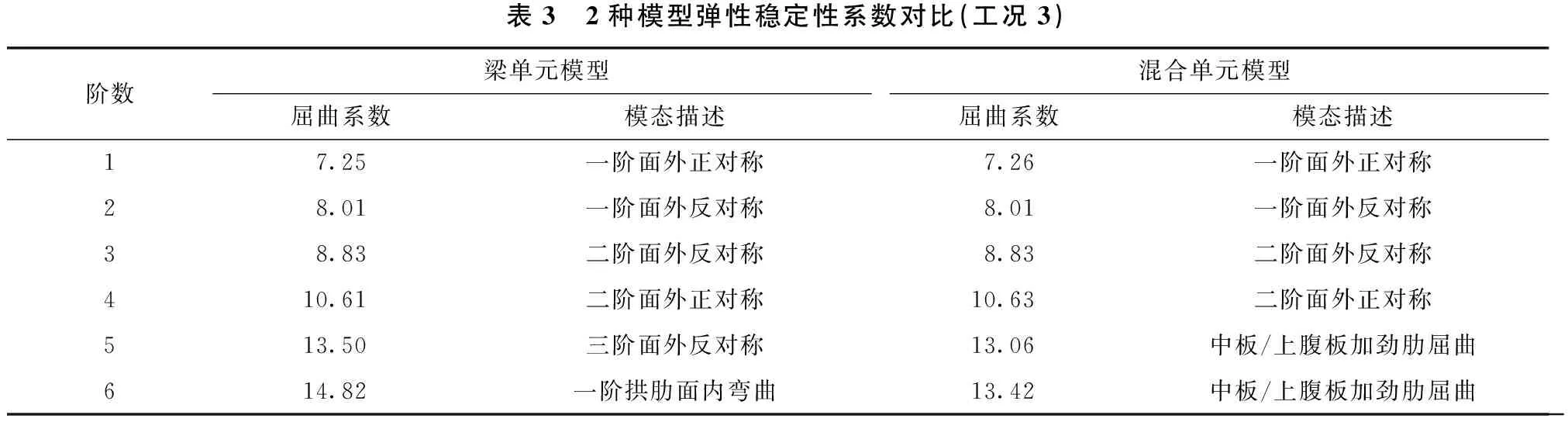
表3 2种模型弹性稳定性系数对比(工况3)阶数梁单元模型混合单元模型屈曲系数模态描述屈曲系数模态描述17.25一阶面外正对称7.26一阶面外正对称28.01一阶面外反对称8.01一阶面外反对称38.83二阶面外反对称8.83二阶面外反对称410.61二阶面外正对称10.63二阶面外正对称513.50三阶面外反对称13.06中板/上腹板加劲肋屈曲614.82一阶拱肋面内弯曲13.42中板/上腹板加劲肋屈曲
3种工况下2种不同模型前6阶稳定性分析结果表明:该桥2种模型前4阶均为整体面外失稳,且数值差异极小,工况2和工况3下,2种模型5~6阶模态有所区别,梁单元模型主要为整体失稳,混合模型则表现出加劲肋局部失稳,且稳定性系数更小。
4 结论
以某大跨径钢拱桥为研究对象,建立混合有限元模型分析其前6阶稳定性,并与梁单元模型进行结果对比,得到以下结论:
1)在恒载工况下,2种模型前5阶振型相同,且屈曲系数相差极小;第6阶振型有所区别,混合有限元模型表现出局部失稳,且屈曲系数较梁单元模型低。
2)在恒载+活载工况下,2种模型前4阶振型相同,且屈曲系数相差极小;5~6阶振型有所区别,混合有限元模型表现出局部失稳,且屈曲系数较梁单元模型低。
3)考虑风荷载后,对结构整体及局部稳定性影响较小,屈曲系数及模态均无明显变化。

