基于CART算法的PVC压延设备状态诊断方法研究
王美林,刘金刚
(广东工业大学信息工程学院,广州510006)
0 引言
近年来,随着中国制造业的转型升级[1],国内众多制造型企业开始沿着制造业信息化、智能方向发展,将现代信息技术与传统制造业向融合,提高生产效率,从而降低生产成本。在工业生产过程中,确保设备维持正常的运转状态是至关重要的。因此,如何准确判定设备是否处于正常运转状态成为了众多企业管理者关心的问题。
现有的PVC压延设备体型庞大、结构复杂、作业流程长,单纯依靠设备操作人员实时诊断[2]设备生产状态是非常困难的。随着物联网技术[3]的发展,PVC压延设备的信息化改造已初步完成,通过各种类型的传感器[4]实时采集PVC压延设备生产时的设备信息并传输到服务器中。因此,可以通过大数据技术对设备历史信息进行分析[5],建立PVC压延设备运行状态诊断模型,完成对设备实时监控。
PVC压延设备运行状态诊断模型属于分类模型,常用的构建算法有逻辑回归[6](Logistic Regression)、决策树(Decision Trees)和支持向量机[7](Support Vec⁃tor Machine,SVM)。由于逻辑回归算法容易欠拟合,精度不高,而SVM算法针对拥有大量训练样本的数据集时运算效率不高。相比较而言,决策树算法决策规则直观且运算效率高,虽然会有过拟合现象,但可以通过集成学习的方式克服。因此,本文通过使用CART算法对历史数据进行分析建立初步设备运转状态诊断模型。引入提升(Boosting)方法,创建多个CART树并进行加性组合,通过构建集体决策模型完成PVC设备运行状态的实时诊断,最后通过的实例测试证明该方法具有较强的实用性。
1 算法描述
1.1 决策树的构建
常见的决策树算法包括ID3、C4.5、CART等,其中C4.5算法是对ID3算法的优化[8],解决了ID3算法在分支过程中总偏向于取值较多的属性,通过计算信息增益比率(gain ratio)来选择分割点,该算法可以用来做多分类决策树。CART算法采用二元分割法,即每次把数据分割成两份,分别进入左子树、右子树最终形成分类二叉树。CART算法通过计算基尼系数增益来确定分割点,在针对大规模样本时,CART算法相较于C4.5算法,不用进行大量的排序运算和对数运算,运算效率会更高。因此,本文使用的决策树算法为CART算法。
CART树具体构建方法如下:
(1)对于一个样本数据集S,分类属性有m个类,记第i个类别的概率为pi,pi的计算方法为属于该类别的样本数除以数据集总样本数。则样本S的概率分布基尼指数定义为:

(2)数据集S中非分类属性K的基尼系数GiniK(S)计算公式为:

S1、S2表示集合S被特征属性K的最佳分割点分割后的两部分,|S1|表示S1中样本的个数。这里的重点在于如何找到最佳分割点对集合S进行划分。有如下3种情况:①当特征属性K只有两种取值类型,则不需要讨论分割点,直接利用上述公式计算即可。②当特征属性K有多种取值类型,则需要对多个取值类型进行二分类划分,得到多种二分类划分方式。利用公式(2)分别计算每个的二分类划分方式的基尼系数,选取基尼系数最小的二分类划分方式作为最佳分割点。③当个特征属性K为数值属性时,需要先对数据先进行排序,按照排列顺序依次用相邻两个数的均值作为分隔点将样本划分为两个部分,计算分割后对应的基尼系数,同样取基尼系数值最小的作为最佳分割点。
(3)对于一个属性K,它的基尼系数增益计算方法是用样本的概率分布基尼指数减去属性K的基尼系数,表达式为:

依次选取基尼系数增益最大的属性作为分类节点对数据集划分为两个子数据集,再在子数据集中对剩余的属性递归调用第二个步骤,当子数据集中的样本全部属于同一类时停止递归调用。
(4)使用CART算法建立分类二叉树用于设备运转状态的诊断,不可避免的便是“过拟合”现象,因此还需要进行剪枝处理。剪枝的基本策略有“预剪枝”和“后剪枝”[9],其区别在于“预剪枝”是在决策过程中当进行结点划分时进行的,当新结点的划分并不能提高决策树的性能提升,则停止划分,并把当前结点标记为叶子结点。“后剪枝”则是先生产一棵完整的决策树,再从下往上考察每个非叶子结点,将该结点的子树标记为叶子结点,若能提升决策树的泛化性能,则去掉子树,将该子树替换成叶子结点。相比之下“后剪枝”的欠拟合风险小,泛化性能优于“预剪枝”。常用的“后剪枝”方法有EBP(基于错误的剪枝法)、REP(错误率降低剪枝法)、PEP(悲观错误剪枝法),CCP(代价复杂度剪枝法)。单棵CART树在后剪枝之后可以缓解过拟合现象,提高分类精度,但分类精度仍然不高。因此本文引入了提升(Boosting)方法,在此也就不再讨论“后剪枝”的具体做法。
1.2 提升(Boosting)方法
对某个数据集的进行分类器的训练的过程中,构造多个精度较低的弱分类器比构造一个高分类精度的强分类器要容易的多。因此,通过使用CART算法构建完一棵CART树之后,改变训练样本的权重,即增加被分类错误的样本比重,降低被分类正确的样本比重,构成新的训练集,再次训练新的CART树,就此便可得到一系列的弱分类二叉树{T1,T2,T3,…,Ti,…},将一系列分类二叉树进行加性组合便可以得出一个强分类二叉树。具体流程如图1所示,其中Wij表示第i次构建弱分类器时,训练集的第j个样本权重。ei表示第i个弱分类器的误差率。ɑi为分类器加性组合时的系数。
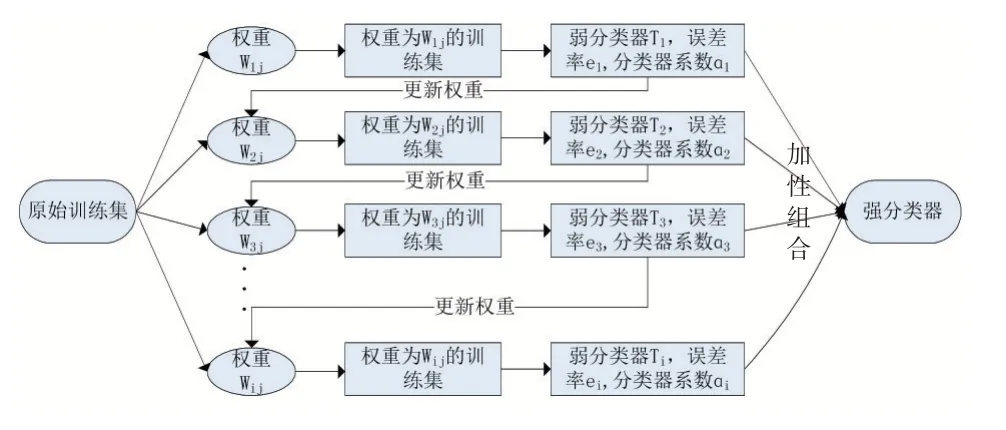
图1 提升(Boosting)方法
误差率ei的计算公式为:

其中,Ti(j)表示数据集S的第j个样本经弱分类器Ti后得到的值,yj表示该样本的真实值,I为指示函数,当Ti(j)=yj成立时I(Ti(j)=yj)=0,反之,当Ti(j)=yj不成立时I(Ti(j)=yj)=1。
系数ɑi的计算方式为:

权重计算公式为:

当i=0时,即数据集S每个样本j的初始化权值为为样本集S的样本个数。Zi为规范因子,计算公式为:

将(5)式代入(6)式与(7)式进行化简可得:

基于CART树的强分类器构建方法如下:
(1)对训练数据集S使用CART算法构建第一棵CART树T1,在构建过程中与原来方法不同之处在于:在使用公式(2)计算基尼系数时需要先使用公式(1)计算基尼指数Gini(S1)、Gini(S2),公式(1)中的第i个类别的概率pi计算方法不再是用属于该类别的样本数除以数据集总样本数,而是求属于该类别的各个样本对应的权重值之和。
(2)利用公式(4)计算第一棵CART树的误差率e1,利用公式(5)计算T1的系数ɑ1,利用公式(8)、(9)计算出第一次迭代后的权值W2j,替换样本S的权值。
(3)对替换权值后的样本S继续使用CART算法构建之后CART树,重复(1)、(2)两个步骤便可得到一系列的弱分类二叉树{T1,T2,T3,…,Ti,…}。
(4)将这一系列的弱分类器{T1,T2,T3,…,Ti,…}加性组合便可以得到一个强分类器:Fi=ɑ1T1+ɑ2T2+ɑ3T3+…ɑiTi,当强分类器对训练集样本的误分类次数达到阈值或训练集样本被完全正确分类时,停止构建新的弱分类器。
(5)最终得到的强分类器函数表达式为:
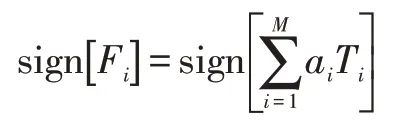
(6)sign为符号函数,表达式为:

2 算法的实现
2.1 数据来源说明
本文所使用的PVC压延数据来自广州佛山某新材料股份有限公司现有的PVC压延线设备监测控制系统,该系统通过各类底层传感器采集生产信息,使用串口联网服务器等设备将各类传感器数据,上传服务器。PVC压延生产线示意图如图2所示。
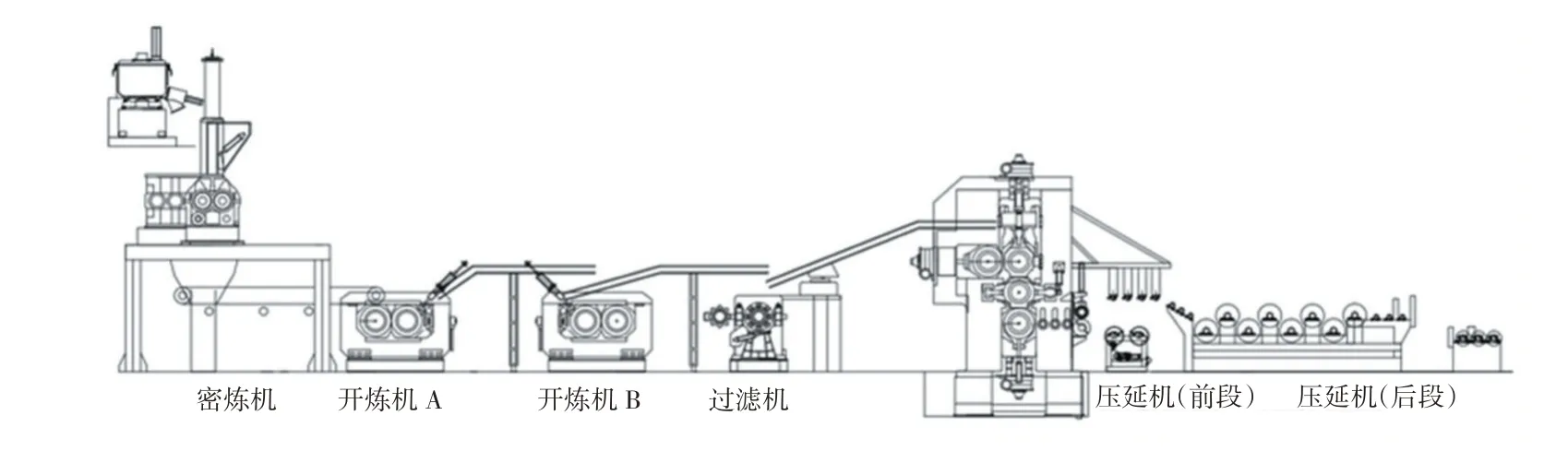
图2 PVC压延生产线
2.2 数据预处理
现有PVC压延线的历史数据均按照采集的时间先后保存在日志文件中,需要通过编程对日志文件进行解析。解析后得到的原始数据集中存在重复、缺失、错误现象,采取如下措施:①如果相邻的几组数据完全一致则合并为一组;②如果数据缺失,用邻近数据均值补全;③如果存在错误数据,错误数据是指数据格式或数据值远远超出取值范围的数据,对该类数据将直接剔除。为了使训练集数据更具有代表性,从2019-2020年的PVC生产线历史数据中按不同的月份和日期和时间段抽取5500组PVC压延设备正常生产时的设备历史数据,从两年期间设备每次发生故障时采集到的数据中等概率抽取4500组设备故障数据组成数据集。将设备正常生产时数据和设备故障时采集到的数据进行随机混合,以其中的7000组数据作为训练集,剩下的3000组数据作为测试集,进行模型的训练与测试。表1为数据集的部分数据情况,运行状态为1代表的是设备正常运行时所采集到的数据,运行状态为-1代表的是设备故障时所采集到的数据。

表1 数据集中部分数据展示
2.3 建立模型
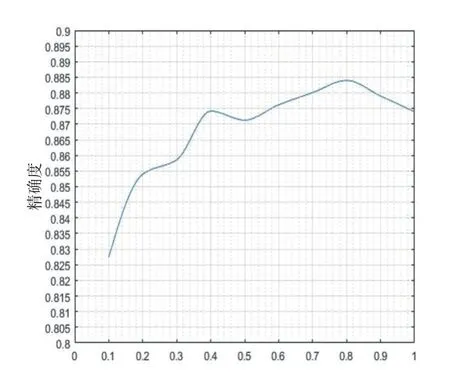
在表1中可以看到,数据集由设备的{电流,温度,速度}以及PVC压延产品的厚度四个属性组成,均为数值属性,因此在构建CART树时符合公式(2)下方的第(iii)种情况,即对每个属性确定最佳分割点时,需要先对该属性下的数据进行排序,按照排列顺序依次用相邻两个数的均值作为分隔点将样本划分为两个部分,第一次构建CART树时,各个样本的权重均为1/10000。按照基于CART树的强分类器构建方法构建强分类器Fi。由于强分类器Fi=ɑ1T1+ɑ2T2+ɑ3T3+…ɑiTi可写成Fi=Fi-1+ɑiTi,为了防止过拟合,在强分类器构建的过程中加入正则化项v(0 在强分类器Fi构建过程中,为了防止拟合现象,需要不停地用测试集对更新的强学习器进行准确度(Accuracy)[10],精确率的表达式为: 其中,TN表示样本实际值为-1,判决值为-1的样本数目。FP表示样本实际值为-1,判决值为1的样本数目。FN表示样本实际值为1,判决值为-1的样本数目。TP表示样本实际值为1,判决值为1的样本数目。TN+FN+FP+TP=测试集样本总个数。 影响强分类器Fi分类精度的因素有两个:弱分类器数目和正则化项。图3表示的是在v=1的条件下,强分类器Fi分类精度随弱分类器数目变化而变化的情况,图中最小的错误率为0.1216,对应的弱分类器数目为第176。弱分类器迭代176次,v=1的详细测试记录如表2所示。 表2 v=1、迭代176次测试记录 图3 强分类器错误率与弱分类器数目关系 从图3可以看出,当弱分类器在v=1的条件下,迭代176次之后出现了过拟合现象,导致强分类器分类精度降低。 由于正则化项v的取值也会影响强分类器Fi分类精度,但在实际测试中,除非v的取值太小,导致迭代1000次还达不到最大值,否则,正则化项v的取值变化对最终分类精度的影响是比较小的,对v采用步进为0.1的搜索方法测试v每次变化时,强分类器Fi分类精度的变化,具体变化情况如图4所示。 图4 精确度与学习率的关系曲线 从图4中可以看出,强分类器分类精确度受正则化项v变化的影响不大,取值范围均在82.5至88.5之间,从v=0.1这个点也可以看出,由于正则化项v取值过小,在迭代1000次弱分类器时仍然处于欠拟合状态。当v=0.8时,强分类器分类精确度取值最大,为88.37%,对应迭代次数为221次,此时具体测试情况如表3所示。此时,强分类器的AUC曲线如图5所示,取值为0.90。 表3 v=0.8、迭代221次的测试记录 图5 强分类器ROC曲线图 工业大数据在未来的制造业发展过程中将发挥越来越重要的作用,成为提升生产效率、完成产业升级的重要手段。本文通过使用基于CART算法的提升(Boosting)方法对PVC压延设备生产历史数据进行分析,构建设备生产状态诊断模型,用于设备生产状态的实时诊断。实验测试表明,该诊断模型的分类精度可达88.37%,AUC值为0.90,判决速度为0.15 ms/条,具有较高的准确率和实用性,也对其他类似的制造型工业生产设备运行状态的判决提供了一种可靠的解决方案。
2.4 模型测试
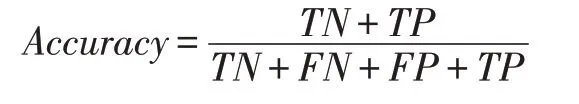




3 结语

