民用飞机机体外部对流换热系数计算方法研究

曹 祎 吴成云

(上海飞机设计研究院，上海 201210)

0 引言

大型民用客机结构的复合材料化已成必然的发展趋势，宽体客机将大规模的使用复合材料。由于复合材料的性能对温度极为敏感，因此飞机结构设计热分析已经成为大型飞机设计和适航认证的最关键部分之一。在计算民用飞机结构温度场中，外部对流换热系数值为设置外部对流边界必须的关键参数，外部对流换热系数值的选取将直接影响计算结果的准确性，从而影响飞机结构强度等重要性能参数。

对于外部对流换热系数计算，需针对地面停机和飞行条件分别考虑。在地面停机条件下，由于风速不大，机身外表面的空气流动是不可压流动，粘性摩擦热很小。在飞行条件下，由于马赫数较大，气流摩擦和压缩引起的气流阻滞导致的气动力加热明显，因此在计算外部对流换热系数时需考虑气体的压缩性和热交换的影响。

地面停机工况的机体外部对流换热系数，目前研究较为成熟，并形成了较为合理简便的计算公式。对于飞行工况，目前通常采用参考温度法。参考温度法为在分析飞行器高速飞行时，考虑其表面产生的热现象及其对表面摩擦力的影响，提出的一种工程估算方法。参考温度法将整个飞行器视为一个质点，根据飞行器高速飞行时表面产生的气动热计算得到外部对流换热系数，因此依据参考温度法计算得到的飞行器机体外部对流换热系数值为平均对流换热系数值。而实际的飞机结构决定了飞机各部位的外部对流换热系数差别很大。若计算时将机翼前部、机翼后部及机身等不同部位的外部对流换热系数设置为同一数值，势必会严重影响计算结果的准确性。

本文以某民用飞机为研究对象，基于理论分析提出一种可用于求解飞行条件下飞机机体各区域外部对流换热系数的仿真计算方法。并应用三维计算流体动力学CFD方法研究飞机外流场，从仿真计算角度对其可行性进行分析，采用理论的参考温度法和传热公式法对极限温差法计算结果的准确性进行验证。三维数值仿真计算采用空气动力学中常用的STAR-CCM+软件。

1 极限温差法理论分析

对于对流换热系数的计算，由传热学原理可知，外部对流换热量计算公式为：

q

=

h

(

T

-

T

)

(1)

式中：q为表面热流量，

W/m

；h为外部对流换热系数，

W/m

·

K

；T为固体壁面温度，

K

；T为流经固体表面流体的特征温度，即参考温度，

K

。

因此参考温度的选取，将直接影响计算得到的外部对流换热系数值。为规避参考温度对计算结果的影响，求解得到准确的外部对流换热系数值，本文基于传热学基本原理，提出了一种可用于计算飞机机体各区域外部对流换热系数的仿真计算方法——极限温差法。

对流换热系数计算公式(1)中包含4个参数，对流换热系数h、壁面温度T、参考温度T和热流量q。在

CFD

计算中，T为飞机壁面温度，属于计算的边界条件；q为飞机内壁面温度通过隔热材料向外的导热，可通过计算求解得到，当计算工况一定时，其为定值。现主要对参数h和T进行研究。

由传热学原理可知，影响对流传热的因素主要包括以下方面：流体流动的起因(强制对流或自然对流)；流体有无相变；流体的流动状态(层流或湍流)；换热表面的几何因素(换热表面的形状、大小、换热表面与流体运动方向的相对位置以及换热表面的粗糙度等)和流体的物理性质(导热系数、动力粘度、密度、定压比热等)。因此，在非自然对流状态下，机体外部对流换热系数值只与飞行高度、飞行速度及飞机结构有关，与飞机壁面温度无关。

参考温度T为流经固体表面流体的特征温度，因此T与飞机蒙皮温度、来流温度、飞行速度及飞机结构有关。通常情况下，参考温度T取为恢复温度T、总温T或来流温度T。根据恢复温度及总温的计算公式，本文假设参考温度计算公式中的恢复系数为一个定值，则参考温度计算公式可表示为：

T

=

T

1+

αMa

)

(2)

式中：T来流温度，

K

；α为恢复系数；Ma为马赫数。

假设壁面温度T与来流温度T温差为c，即T的计算公式为：

T

=

T

c

(3)

将公式(2)和(3)带入公式(1)，即可得到对流换热系数计算公式为：

(4)

由参数分析可知，当飞行工况一定时，q为一定值。此时，公式(4)为一双曲函数。由双曲函数特性可知，当c-αTa趋于正无穷大或负无穷大时，h值趋于一定值。而飞行工况一定时，αTa也为一定值，因此当温差趋于正无穷大或负无穷大时，

h

值趋于一定值，此即为飞机在某一飞行高度及飞行速度工况下的外部对流换热系数值。

2 计算方法可行性分析

基于软件

STAR

-

CCM

+，以某客机常温天巡航飞行4 000

m

，飞行速度为158.22

m/s

工况为例，从仿真计算角度对本文提出的用于求解飞机机体各区域外部对流换热系数的极限温差法的可行性进行分析。由计算原理分析可知，计算时温差取为正无穷大或负无穷大，即可计算得到对流换热系数所趋于的定值。由于当温差取为负无穷大时，壁面温度会小于0

K

，此时数据无物理含义，因此温差只向正无穷大方向取值。本文中壁面温度与环境温度的温差分别取为-100 ℃、-2 ℃、0 ℃、2 ℃、5 ℃、10 ℃、100 ℃、200 ℃、500 ℃、1 000 ℃、1 200 ℃和1 500 ℃，得到的飞机机体各区域外部对流换热系数随温差的变化如图1所示，其中具体工况如表1所示。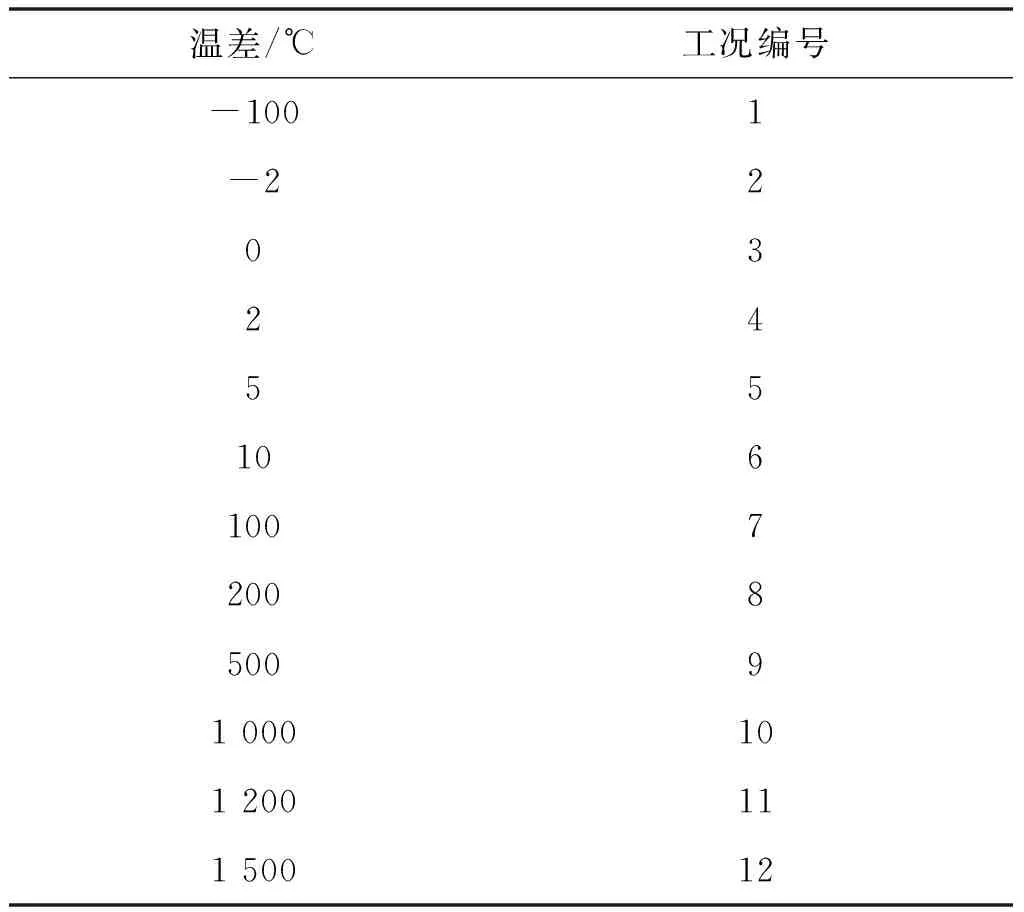

表1 计算工况

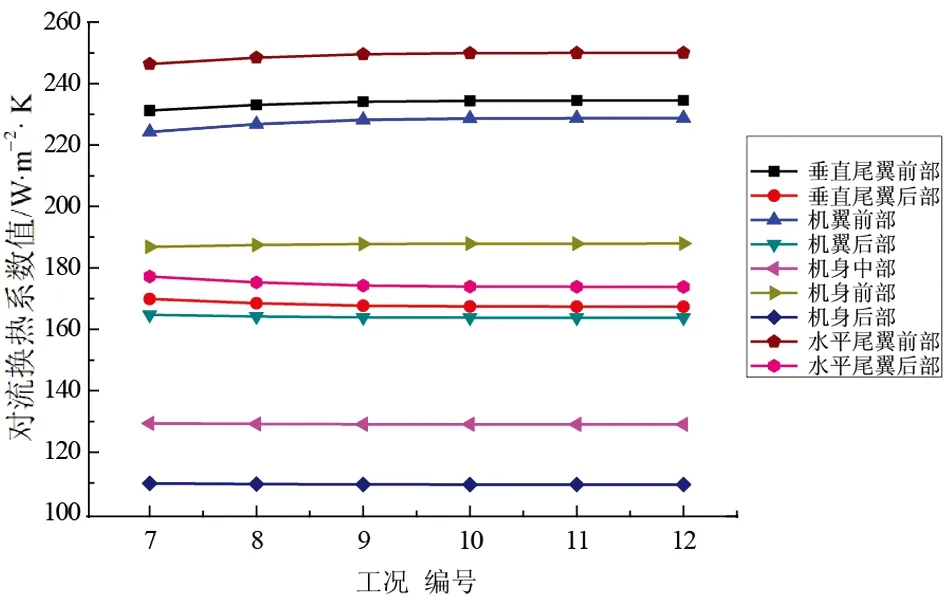
(a)全工况温度范围

(b)大温差工况温度范围图1 飞机机体各区域外部对流换热系数值随温差变化

由图1可知，飞机机体各区域的对流换热系数值不同，但变化趋势基本相同。即随着温差的增大，飞机机体各区域的外部对流换热系数绝对值先增大后减小，当壁面温度与环境温度的差值足够大时，飞机机体外部对流换热系数值趋于稳定。此时，飞机机体外部对流换热系数值仅与飞行高度、飞行速度及飞机蒙皮的位置有关。即从仿真计算角度证明了极限温差法的可行性。

3 计算结果准确性验证

本文采用理论的参考温度法及传热公式法对本文提出的用于求解飞机机体各区域外部对流换热系数的极限温差法的准确性进行验证。

3.1 计算模型

计算时采用壁面函数法求解边界层内的流动与换热，选取稳态

SSTk

-

ω

模型。计算域网格划分采用

polyhedral

格式，并对机翼、水平尾翼、垂直尾翼、发动机、吊挂结构及尾流区域进行不同程度的加密处理。

3.2 速度边界

在速度包线范围内，选取常温天巡航飞行4 000

m

，飞行速度为158.22

m/s

的工况，计算域边界条件设置如表2所示。

表2 边界条件

3.3 仿真计算结果及验证

下文通过参考温度法及传热公式法对本文提出的极限温差法进行验证。

由于飞机不同位置机体结构外流场的流速差异较大，根据计算所得流场，将飞机机体结构划分为以下部分：机翼前部、机翼后部、水平尾翼前部、水平尾翼后部、垂直尾翼前部、垂直尾翼后部、前机身、中机身、后机身及其他区域。针对验证工况常温天巡航飞行阶段飞行高度4 000

m

，飞行速度为158.22

m/s

，求解得到基于传热公式法与极限温差法的飞机机体各区域外部对流换热系数值，如图2所示。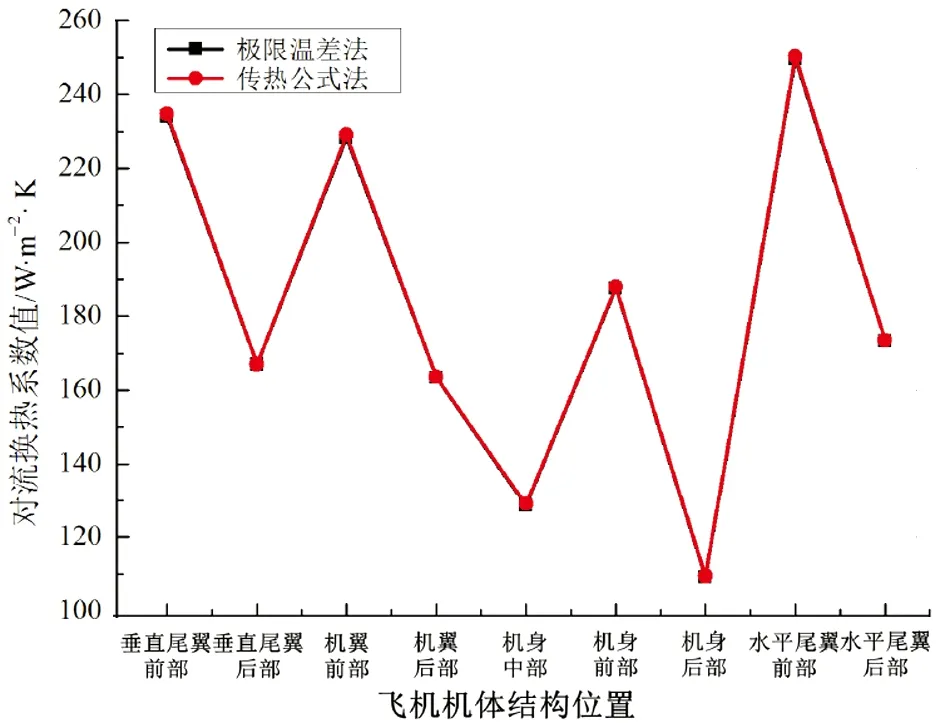

图2 极限温差法与传热公式法计算结果对比

参考温度法计算对流换热系数是按照流体沿平板强迫流动情况处理，因此可认为基于参考温度法计算得到的对流换热系数为基于机身的平均对流换热系数。根据参考温度法，求解得到验证工况下飞机机体外部对流换热系数的理论值。根据传热公式法及极限温差法，求解得到相同工况下，基于面积平均的飞机机身对流换热系数模拟值。将理论值与模拟值进行对比，计算结果如表3所示。

表3 飞机机体外部对流换热系数模拟值与理论值对比

由表3中数据可知，传热公式法和极限温差法得到的飞机机体外部对流换热系数值基本相同，且不同模拟值与理论值之间的差值均约为理论值的8

%

，因此可认为本文提出的极限温差法计算得到的飞机机体外部对流换热系数结果与理论值基本吻合。

4 结论

本文以某民用飞机为研究对象，基于理论分析提出一种可用于求解飞行条件下飞机机体各区域外部对流换热系数的计算方法—极限温差法，并采用

STAR

-

CCM

+软件对飞机外流场进行研究，从仿真计算角度对其可行性进行分析。采用参考温度法和传热公式法对此仿真计算方法的结果准确性进行验证。结果表明，传热公式法和极限温差法得到的模拟值基本相同，且不同模拟值与参考温度法的理论值之间的差值均约为理论值的8

%

，极限温差法计算结果与理论值基本吻合。