低频可控震源激发信号特征及高精度动态监测应用

王力伟 李丽 杨微 王宝善 黄柳芳

摘要：通过实验测试了国产KZ28LF低频可控震源在线性升频、伪随机编码和单频3种激发模式下的信号特征及在地下介质高精度动态监测中的应用效果。结果表明：①线性升频和伪随机编码激发模式可稳定激发1.5～12Hz的低频信号，近场信号互相关系数大于0.95的分别占81%和63%，信号能量在9～12Hz较强、在1.5～9Hz较弱，低频外传能量较弱，而单频激发时高次谐波能量较强，信号重复性较差。②相干法和反褶积法均能压缩震源子波，恢复介质真实响应，相干法的结果重复性和信噪比最高，反褶积法保幅和保相效果最好。③叠加后探测距离可达20km，波速变化探测精度达10-。

关键词：低频可控震源;聚类分析;反褶积;加权相位叠加;波速变化;高精度动态监测

中图分类号：P315.3文献标识码：A文章编号：1000-0666（2021）04-0622-13

0引言

利用地震波高精度动态监测地下介质物理性质及其变化是人们认识地球物理过程的重要手段。实现地下一定目标深度的高精度动态监测，需要能稳定激发、高度重复、宽频带、高信噪比和高时间服务精度信号的地震震源。天然震源如背景噪声和重复地震已广泛应用于与火山喷发（Bren—guier et al，2014）、断裂带破坏和愈合（Peng， -Zion，2006;Chaves et al，2020）、流体运移（Niu et al，2003）、大地震（Liu et al，2014;Li et al， 2017）和地壳介质受外力加卸载（Hillers et al，2015;Mao et，2019）等相关波速变化研究中。但背景噪声易受噪声源变化及其能量分布影响（Zhan et al，2013），重复地震会受到定位精度和时空分布限制（Liet al，2017）。与天然震源相比，人工震源激发位置、深度和激发时间都精确已知，且可与流动台阵组成高质量观测系统，是地下介质高精度动态监测的首选震源（Chen et al，2017）。一些学者使用压电陶瓷、电动落锤、气枪和精密常时可控震源等不同类型的人工震源，以10-5～10-的精度观测到与地震相关的短期波速变化（Niu et al，2008;张元生等，2017;Wang et al，2020），以及与大气压（Silver et al，2007）、温度（Wang et，2020）、水文（Yang et al， 2018）、固体潮（mamura et al，2003）等相关的不同尺度的波速变化。

可控震源是另一种广泛应用于地球物理勘探的人工主动震源（Sallas，2010），根据驱动方式的不同，可分为液压式、电磁式以及精密可控震源3种，与精密常时可控震源相似，其激发信号精密可控，可激发出具有一定持续时间、瞬时能量密度低、高度重复的地震波（陶知非，1995）。其中，液压式可控震源还具有扫描信号可精确设计，激发信号低频能量强、频带宽、分辨力高和作业方便等优点，已是全球陆上使用最广泛的机械震源（Krohn et al，2010）。可控震源已被尝试用于局部尺度的地下介质时变特征研究，如Clymer和McEvilly（1981）利用可控震源观测到可能与地震相关的0.2～0.5ms的走时变化;Korneev等（2000）利用横波可控震源通过连续监测圣安德烈斯断裂内部介质波速变化来研究地震成核过程，发现断裂带引起的波速变化达6%;McCartney 和Cox（2013）利用可控震源作为重复加载源，研究土层的液化响应;Pevzner等（2011）利用可控震源连续监测CO2的驱油过程。

常规可控震源由于机械和液压系统的限制，激发信号频带范围通常为8～300Hz，很难激发低于8Hz的低频信号（Sallas，2010;Wei，Phillips，2013）。低频可控震源是指工作频率低频極限达6Hz以下的震源，因低频信号传播过程中不易耗散和衰减、穿透力强、有效传播距离远，在区域尺度探测中具有较大优势。中石油东方地球物理公司在KZ28可控震源车基础上，生产的KZ28LF新型低频震源成功实现了1.5Hz的低频信号激发，是当时全球唯一针对3Hz以下低频设计的可控震源（陶知非，徐小刚，2017）。与其它震源相比，KZ28LF具有更宽的激发频带、更低的信号畸变和更高的信号重复性，稳定的低频信号使区域尺度结构成像和高精度动态监测成为可能。

为测试KZ28LF激发信号特征及其在高精度动态监测中的应用效果，笔者于2014年11月在河北徐水开展了连续激发和接收实验。本文分析了其激发信号特征;使用波形互相关和聚类分析方法评估了激发信号的重复性和不良激发班次的剔除方法;测试了互相关、移动窗口互相关、相干法和反褶积4种信号压缩方法对线性升频、伪随机编码和单频3种激发模式的使用效果;测试了不同信号叠加方式下低频信号的传播距离;最后使用互相关时延检测方法分析了其在地下介质高精度动态监测中的应用效果。

1工作原理和数据

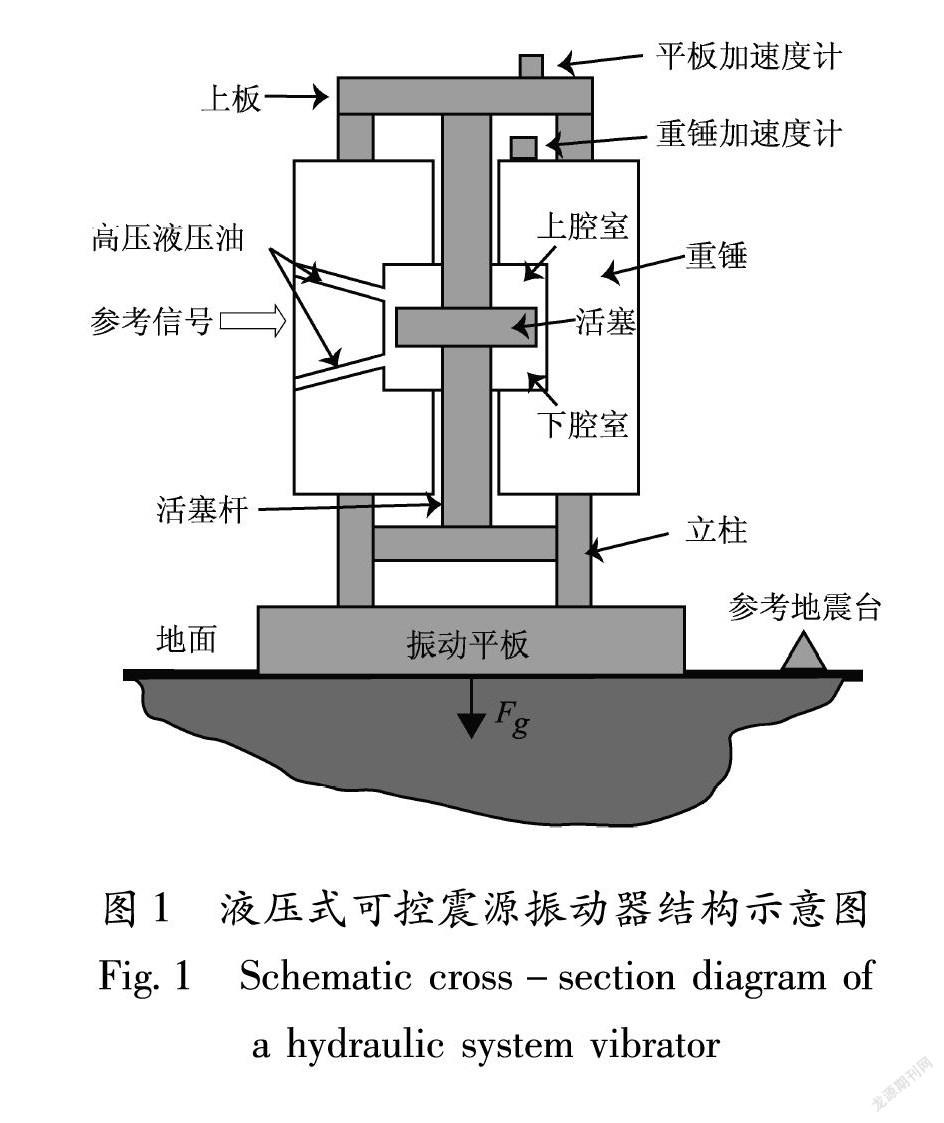
液压式可控震源集电子、机械和液压系统为一体，主要包括电控箱体和振动器（图1）两部分（Sallas，2010;Wei et al ，2010;陶知非，徐小刚，2017）。其中电控箱体产生线性或非线性参考信号，经电液伺服阀生成液压油流信号，高压液压油交替进入振动器重锤内的上腔室和下腔室，并驱动重锤做上下往复振动，而活塞杆与上板、立柱和振动平板等刚性连接，因此，重锤振动信号便通过与大地紧密耦合的振动平板传入大地。电控箱体通过实时监控设置在振动器重锤和平板上的加速度传感器等反馈信号，按照Sallas模型精确控制振动器的工作状态（Sallas，2010），确保振动器的实际振动信号与输入的参考信号相符。

液压式可控震源的工作状态一般使用震源特征信号来描述，主要包括输入的理论参考信号，重锤加速度计记录的重锤信号，平板加速度计记录的平板信号以及根据重锤加速度和平板加速度矢量合成的地面力信号（Sallas，1984）。地面力信号代表被平板下的近地表弹性介质转换为的弹性地震波。因此，数据处理中一般使用地面力信号作为参考源信号进行子波压缩处理（Brittle etal，2001），也可在震源车附近架设台站，用记录的近场信号作为参考信号进行子波压缩处理（Poletto et al ，2016）。

为测试低频可控震源激发信号特征及其在区域地下结构和断裂带应力变化的监测能力，2014年11月，笔者联合中国石油集团东方地球物理公司，在河北省保定市徐水区北奥特车试车场内开展低频可控震源连续激发实验（图2）。实验采用1台载荷为26t的KZ28LF低频可控震源，该震源最大静载压重达281kN、液压峰值力达276kN、重锤质量为4445kg、平板质量为1724kg、激发频带1.5～86Hz、全流量最低频率低于3Hz（陶知非等，2010）。实验采取独立扫描作业方式（表1），使用3种震源扫描信号进行连续激发（Cunningham ，1979;Dean，2014）。为增加振动平板与地表土层的耦合效果，实验采取空震的方式压实浅表土层。接收系统采用流动地震台，跨安新断裂和徐水断裂（杨承先，1983），分别布设在偏移距2、5、10和20km位置（图2），其中D20km台站为基岩台，其它为土层台。为记录震源车近场震源时间函数，在距离震源车10m处布设了参考地震台（D0km）。观测地震计为GURALP -40T（10m、20km距离处）和GURALP -6TD（2、5和10km距离处），仪器频带范围分别为2s～100Hz，20s～100Hz，数据采集器为rEFTEK -130B，采样率为200Hz，GPS采取连续授时模式。

2研究方法

液压式可控震源得益于扫描信号精确可控、机械系统和耦合条件稳定不变的优点，能持续稳定的激发出具有一定持续时间的、带限的、瞬时能量密度低的高度重复信号。但因机械、电气和平板耦合等多种原因，外传信号会出现出力不均、畸变大和基波能量弱等现象（Nagarajappa，wilkin-son，2010）。为分析其激发信号特征，本文采用短时傅里叶变换时频分析方法，分别分析了理论参考信号、实际出力信号和近场参考信号在线性升频、伪随机编码和单频3种信号扫描模式下的信号特征，然后利用D0km台记录的垂直分量波形，使用波形互相关和聚类分析方法研究了激发信号的重复性和不良班次的剔除方法。

2.1激发信号特征及数据筛选方法

聚类分析是根据一个类中对象间的相似程度，将类中的对象分成更多子类的过程，其目的是使类内部对象间的距离最小，不同类之间的距离最大（Sneath et al ，1973），目前已广泛应用于相似地震识别（王伟涛，王宝善，2012）、震相拾取（Rowe et al ，2002）、精定位（Son et al ，2018）和地震成核过程研究（Zaliapin，Ben-Zion，2013）。

聚类分析方法使用基于树状结构的凝聚式层次聚类方法（Rowe et al ，2002）。首先，使用移动窗口互相关方法，计算了任意两个事件之间的归一化最大互相关系数，构建了相似性矩阵c，同时计算了每一次事件与将全部事件线性叠加构建的参考事件之间的最大互相关系数，互相关计算窗口为0～20s，移动步长为0.005s，事件之间振幅的差异被忽略，因为波形相位的一致性对于叠加和互相关时延估计更重要（Wang et al ，2008）。其次，计算了距离矩阵dn=1-c，这个矩阵包含所有即将聚类事件之间的相似距离，并再次计算事件之间、类之间、事件和类之间新的距离，反复迭代，直至所有事件均归为一类为止。两个事件之间距离由距离矩阵中对应元素确定，但是两类之间的距离使用3种定义模式（Rowe et al ，2002），最严格的是最大距离法，即类间距离是两个类之间所有事件的最大距离：

最宽松的是最短距离法，即类间距离使用两个类间所有事件的最小距离：

式中：C、C为不同的类;x1和x1为类中不同对象;d（x，x）为对象间的距离;D为类间距离。当所有事件归为一类后，通过设定相似度距离阈值a，便可得到此标准下的類别数和分属各类的事件（Lance ，williams，1967;Rowe et al ，2002）。使用聚类分析方法避免了互相关计算时参考波形的选取，能更合理地得到震源车激发信号的稳定性分布特征。

聚类分析前以近场信号的起跳时刻为参考零点，使用移动窗口互相关方法提取了各次事件的精确激发时刻，相关系数计算窗长20s，提取阈值0.955，滤波范围单频激发信号为1～2Hz，其它为1～13Hz，并裁剪了激发零时刻前5s、后25s总长度为30s的事件波形用于后续分析。通过波形互相关方法，共提取出线性升频激发事件431个、伪随机编码激发事件121个和单频激发事件400个，经与震源车激发班报进行对比，发现通过波形互相关方法不但可以100%的提取出激发班报给出的事件目录，还能剔除一些发生严重畸变的激发班次。

2.2震源子波压缩方法

可控震源激发信号为长时间的连续调频信号，因此，为恢复介质的真实响应，必须对接收到的信号进行子波压缩处理（Wapenaar，Fokke-ma，2006;杨微等，2013）。本文选用D0km台记录的近场信号作为子波压缩的参考信号，分别测试了互相关、短时互相关、相干和反褶积4种方法在线性升频、伪随机编码和单频3种激发模式中的应用效果，4种信号压缩方法的计算基本原理为：

互相关法压缩子波是基于可控震源扫描信号的自相关函数可近似为零相位Klauder子波的假设（Klauder，1960），利用互相关法将长时间记录的扫描信号压缩为一个类似脉冲信号：

式中：U（r，t）是仪器记录项;S（s，t）是近场震源项;G（r，s，t）是介质经验格林函数，其包含直达体波、面波及多次波等介质的全部响应信息。互相关计算相当于经过扫描信号频谱的2次方滤波，互相关结果可以压制相关噪声，但其结果与扫描信号的形状有关，会改变各频率的能量（Brittle et al， 2001; Wapenaar et al， 2010）

短时互相关法与互相关法计算过程类似，但每次仅计算第i个窗口w（n）内，仪器记录信号U（r，t）和近场震源记录信号S1（s，t）对应部分的互相关C（r，s，t），并以一定的步长滑动互相关计算窗口，遍历整个记录道，然后将每个窗口内的互相关函数叠加得到平均互相关结果（Bensen et al ，2007;Tal et al ，2011）：

相干法是根据地下介质信号传播的褶积模型和互相关原理，将仪器记录信号U（r，t）和近场震源记录信号S（s，t）在频率域表示为：

式中：分子项与频率域互相关相同;分母是台站记录信号和震源车激发近场信号的振幅谱。因此，通过频域振幅谱相除，相干法去除了信号的振幅信息，仅保留了相位信息，能显著压制噪声和道间振幅不一致的影响（Cao，2016）。

反褶积法同样基于地下信号传播的褶积模型，在频域将震源车至台站间的介质格林函数G（r，s，ω）表示为：

为避免除法数值运算的不稳定引起的信号畸变，采用频率域水准反褶积方法，引入水准比例因子c（Mehta et al ，2007）：

式中：max为求最大值。通过水准比例因子c将低于该阈值的振幅提升到阈值水平，以保证数值运算的稳定性。最后再通过傅里叶反变换到时间域，得到震源车到接收台站之间的格林函数G（r，s，t）与相干法类似，反褶积法也能显著消除震源子波不一致和噪声的影响，反褶积结果只与扫描信号的频带有关，与振幅谱的形状无关，且保幅和拓频效果较好，广泛应用于地震资料的高保真数据处理（Brittle et al ，2001）。

2.3信号增强方法

低频可控震源单次激发信号能量较弱，为增强有效信号、压制噪声，使用线性叠加法和加权相位叠加法来提高信噪比，以测试其最远探测距离。研究表明，线性叠加有用信号随叠加次数N成N倍增长，而随机噪声信号随叠加次数N成√N倍增长，因此線性叠加法可使结果信噪比增加N倍（蒋生淼等，2017）。直接线性叠加法给记录的每个采样点赋予了相同的叠加权重，加权相位叠加法可根据信号和噪声的相关程度大小，分别赋予不同的权重，可更有效地压制噪声，增强远距离台站微弱信号的检测效果（Ken-nett，2000）。

2.4走时变化测量方法

为测试低频可控震源在地下介质高精度动态监测中的应用效果，使用互相关时延检测方法分别测试了3种激发模式下走时变化的检测精度。该方法采用滑动窗口互相关技术（Wang et al ，2008），通过测量不同窗口内比较波形和参考波形的互相关系数，最大互相关系数对应的走时延迟即为走时变化d，进而得到一定窗口范围内的平均dt及其误差估计。采用互相关方法进行波形时延检测的误差理论下限可由Cramer -Rao公式估算（Niu et al， 2008; Wang et al， 2008）

式中：f为震源的中心频率;B为频宽比;SNR为信噪比;p为波形的互相关系数;T为计算互相关的窗长。从式（8）可见，提高激发信号的主频、频带宽度、信噪比和互相关系数均可大大降低走时测量的误差。

因反褶积法可以有效抑制源致谐波干扰、拓展频带宽度，恢复的振幅和相位响应更接近介质真实的格林函数，且可消除由于机电系统、平板耦合和近地表介质物理参数变化等震源处的变化而造成的震相到时的微弱变化（Ikuta et al ，2002;Lebedev ，Beresnev，2004），因此，测量信号使用信噪比较高的D2km台与震源车附近参考台的垂直分量反褶积处理结果。为进一步降低震源附近近场信号变化对走时变化测量的影响，对使用聚类分析提取的优良激发班次：①采用波形互相关技术将参考台的波形对齐。②将裁剪出的D2km台的事件波形和参考台的事件波形进行反褶积，线性升频和伪随机编码滤波范围为1～13Hz，单频为1～2Hz。③通过叠加构建走时计算的参考波形和比较波形，参考波形是将全部波形线性进行叠加得到，比较波形是将相邻震次进行线性叠加得到，且仅使用比较波形和参考波形的互相关系数大于0.91的事件进行走时变化测量。④选择信噪比和互相关系数均较高的4.1～4.5s窗口范围计算3种激发模式下的平均dt、平均互相关系数和标准差。线性升频和伪随机编码模式dt计算窗长为0.4s，单频模式dt计算窗长为0.9s，窗口移动步长0.005s，为获取更高精度的走时变化，对互相关计算结果进行了5倍采样率的余弦函数内插（Wang et al ，2008）。

3研究结果

3.1激发信号特征

线性开频、伪随机编码和单频模式下激发信号频谱特征如图3所示，从图3a可见，线性升频激发模式下，实际出力信号和近场信号激发频率随时间变化线性增大，信号主频在1.5～12Hz，除能量较强的基波外，还存在2阶、3阶等高阶谐波，谐波能量较弱。近场信号能量集中在9～12Hz，在1.5～9Hz低频段，近场信号能量不如出力信号强。虽然震源车在前0～15s加在平板上的力较大，且75%振动时间集中在1.5～9Hz，而在9～12Hz仅振动5s，占25%，低频信号外传能力仍需改进。从图3b可见，伪随机编码激发模式与线性升频激发模式类似，实际出力信号主频集中在1.5～12Hz，在4Hz和11Hz存在2个能量主峰，近场信号能量集中在9～12Hz，能量峰值随时间变化特征与出力信号符合较好，无明显谐波干扰，抗干扰性强，编码效果较好，而1.5～9Hz低频信号外传能量相对较弱。从图3c可见，单频激发模式下，理论扫描信号能量都积累到1.5Hz，频率域呈现单一峰值，主频集中在1.5Hz，但由于震源是机械震源，除1.5Hz基频外，出力和近场信号还存在能量较强的高阶谐波，谐波频率是基波频率的整数倍，高能量的谐波耗散了大部分激发能量，降低了基波出力的信噪比。

综上，从实际出力信号看，伪随机编码激发模式抗干扰能力最强，线性升频模式次之，单频模式最差，其谐波干扰最严重。这是由机械震源的Sallas力学模型决定的，如液压系统的非线性、机械系统的窄带限制、输出信号振幅和相位畸变、平板的低刚度、近地表耦合条件的非线性、激发参数等，均可导致可控震源在振动出力时包含许多谐波畸变，尤其是在低于20Hz的低频段（Weietal，2010，2013）。从近场记录信号看，因基波和谐波能量一起辐射进入大地，线性升频和伪随机编码模式下近场信号能量均集中在9～12Hz，外传效果较好。1.5～9Hz低频信号以及单频激发模式1.5Hz的低频信号受能量较大的源致谐波干扰影响较大，外传能量相对较弱。

3.2重复性分析及数据筛选

图4a给出了3种激发模式下，每次激发的近场信号相对通过叠加构建的参考信号的互相关系数分布。从图4a-1可见，线性升频激发时重复性最好，相关系数在0.95以上的占81%，0.90以上的占88%，信号畸变发生在第48到100次激发之间，畸变发生时段较集中，且因实际出力信号畸变造成，调整激发参数后，激发波形非常稳定。伪随机编码激发重复性次之（图4a-2），相关系数在0.95以上的占63%，0.90以上的占68%，信号畸变发生在第80次激发之后。单频激发重复性最差（图4a-3），17%的相关系数在0.85以上、42%在0.8以上、57.7%在0.75以上，相关系数在整个激发时段较离散。

相似度距离阈值α的不同选取会影响类和类内事件的数目，为评价低频震源车激发信号的重复性，笔者从0.8至0.995，每隔0.005计算了不同相似度阈值α下的聚类结果，并统计了类内对象数目最多的前4个类以及剩余事件数目占全部事件的百分比，根据类的数目和对象数的分布情况选择最优的阈值a（图4b），其中线性升频和伪随机编码的类间距离采用严格的最大距离法，单频由于相似性较差，采用宽松的最短距离法。聚类结果显示，线性升频激发模式下a取0.925，87.7%的事件能聚为一类（图4b-1），其它类的数目虽较多，但每一类的事件数却较少，可见采用线性升频激发模式时，激发信号高度重复。伪随机编码激发模式下a取0.945，66.1%的事件能聚为一类（图4b-2），且大多是前84次激发的信号，后37次激发信号不稳定，可能因振动系统或平板耦合问题造成信号畸变较大。单频激发模式下a取0.885，51.3%的事件能聚为一类（图4b-3），但其它事件也大多自成一类，说明单频模式虽能稳定激发1.5Hz的低频信号，但重复性较差。图4c显示了该阈值下，数量最多的前5个类的波形特征，其中，第1类是高质量的激发班次，其它多为背景噪声、无出力、畸变大等不良激发班次。

可控震源的失效模式可分为瞬间崩溃式失效和渐变失效（陶知非，徐小刚，2017），可控震源激发时通过多种实时质控方式保证激发信号质量（王秋成等，2019）。从聚类分析结果看，KZ28LF低频可控震源通过实时质控及时调整激发参数，可以稳定激发高度重复的线性升频和伪随机编码信号，使利用叠加技术增加信噪比进行区域尺度探测和介质时变特征研究成为可能。本文使用聚类筛选的378个线性升频激发事件、80个伪随机编码激发事件和205个单频激发事件用于后续研究。

3.3震源子波压缩方法

图5给出采用不同信号压缩方式D2km台垂直分量波形的处理结果，数据处理包括去均值、去倾斜、带通滤波（线性升频和伪随机编码1～13Hz带通滤波，单频1～2Hz带通滤波），然后将D2km台记录的事件波形和D0km台相应的事件波形进行子波压缩处理，并将50次计算结果进行线性叠加。从图5a可见，对于线性升频激发模式，4种信号压缩方法均能正确压缩震源子波，得到介质响应信息，互相关和短时互相关法结果相似，恢复信号的体波振幅较大，面波振幅较小，相干法和反褶积法计算结果相似，但相干法得到的体波振幅较大，面波振幅相当，反褶积法计算结果的保幅和保相效果最好，体波和不同阶次的面波信号幅度恢复均较好（图5a-1）。从图5b可见，对于伪随机编码激发模式，4种方法均能正确压缩震源子波，互相关和短时互相关法结果相似，能正常恢复出体波信号，但恢复的面波信噪比较低，而相干法和反褶积法均能较好地恢复信号，但相干法得到的体波振幅较大，面波振幅相当，反褶积法计算结果的保幅和保相效果最好。从图5c可见，对于单频激发模式，相干法和反褶积法均能正确压缩震源子波，但相干法得到的信噪比更高，互相关和短时互相关法压缩结果较差。总之，4种方法中，相干法和反褶积方法使用范围更广，通过计算恢复后信号的波形互相关系数和信噪比，发现相干法得到结果的重复性和信噪比最高，反褶积法保幅和保相效果最好。

3.4信号传播距离

在线性升频激发模式下，低频可控震源经反褶积处理后的信号经378次线性叠加和加权相位叠加后的记录剖面图如图6所示。从图中可见，采用加权相位叠加后，信噪比相对直接线性叠加得到了较大提高，经过378次叠加后，20km范围内的台站能记录到有效信号。顾庙元等（2016）在地学长江计划安徽实验中，使用EV56低频可控震源和更长的仪器观测测线，发现通过时频率相位加权叠加，200多次叠加后可在50km范围内提取到有效信号。

3.5走时变化测量

本文使用D2km台垂直分量反褶积恢复的4.0～5.1s窗口内的面波信号进行走时变化测量（图6红色方框），从垂向-径向的质点运动图可见（图6c），其为基阶瑞雷面波（Godfrey et al ，2017）。为提高比较波形的信噪比和相关系数，对相邻震次的信号进行了线性叠加，图7a-1、b-1和c-1展示了4.0～5.1s窗口内不同叠加次数的比较波形和参考波形的互相關系数分布图。由图可见，当线性升频模式叠加15次，伪随机编码和单频模式叠加20次可显著降低相关系数小于0.9的事件比例。线性升频模式平均激发间隔为44.7s，15次叠加相当于11.2min的平均;伪随机编码模式平均激发间隔29.4s，20次叠加相当于9.8min的平均;单频激发模式平均激发间隔82.3s，20次叠加相当于27.4min的平均。最后使用信噪比和互相关系数均较高的4.1～4.5s窗口范围计算了3种激发模式下的平均dt、平均互相关系数和标准差。

由图7a-2、b-2和c-2可见，3种激发模式d集中在±10ms之间，平均走时约为4.3s，相对波速变化和相对走时变化关系为：8v/v=-8t/t，因此，相对走时变化和相对波速变化范围约为0.23%。从dt互相关系数来看，扫频和编码模式互相关系数相对较高，大多在0.95以上，单频互相关系数较低，大多在0.84以上。

从dt测量误差来看（图7a-3、b-3和c-3），线性升频和单频模式误差为0～9ms，伪随机编码模式的误差为0～7ms，线性升频模式误差小于其均值2.1ms的占比为72.3%，小于1ms的占比为42.9%，伪随机编码模式误差小于其均值2.9ms的占比为63.1%，小于1ms的占比为17.5%，单频模式误差小于其均值4.5ms的占比为56.7%，小于1ms的占比为1.6%。因测量窗口中心走时是4.3s，因此1ms、2ms、3ms和4.5ms的走时测量误差分别相当于2.3×10-4、4.6×10-4、6.9×10-4和1.0×10-3的相对走时变化和相对波速变化测量误差。从测量误差来看，线性升频模式因波形相似性高，测量精度最高，伪随机编码模式其次，单频模式因波形相似性低且频带窄，测量误差最大。

本文线性升频和伪随机编码模式f0≈5Hz，B≈8，SNR≈50，p≈0.97，T≈0.4s，代入式（8）计算得到时延估计误差的理论值约为5.6×10-4s，而观测使用的RefTek -130B数采钟差小于10μs（Wang et al ，2020），因测量窗口中心走时是4.3s，因此相对走时变化的理论误差为1.3×104，可见实测误差和理论误差相近。从图7a-2、b-2和c-2可见，不同激发模式观测到的dt随时间变化存在约25min的周期，单频激发模式存在约1h的周期，将线性升频模式相邻班次的叠加次数增加至35次，约相当于26min的平均，dt计算结果也存在约1h的周期成分，不同激发模式观测到的类似现象也印证了观测到的信号的真实性。

4讨论

本文实验表明，低频可控震源能以线性升频和伪随机编码模式稳定激发频率在1.5～12Hz的低频信号，激发数据经过严格筛选后，波形互相关系数分别优于0.925和0.945，叠加后探测距离可达20km，能以（2～7）×10-4的测量精度探测到2.3×10-3的相对波速变化。低频可控震源经过精细处理后，能达到其它人工震源相似的重复性和波速变化探测精度，不仅如此，低频可控震源扫描信号可精确设计，作业方便，对场地要求低，且能以低能量密度稳定激发低频信号，特别适合区域尺度的断裂带精细结构及断裂带内部大震成核过程的应力变化研究（Korneev et al ，2000）。同时，由于低频可控震源瞬时能量密度低，场地破坏小，也可适用于滑坡观测，谢凡等（2020）通过背景噪声互相关干涉测量发现，滑坡失稳前存在大于1%波速相对变化。低频可控震源发展迅速，是当今勘探装备的研究热点，国内低频可控震源在KZ28LF之后又有了发展，LFV3激发频率范围为1.5～120Hz，EV56激发频率范围为1.5～190Hz，输出力平均畸变降低了10%，不用特殊设计的扫描信号就可以稳定激发1.5Hz的低频信号（陶知非等，2018）。因此，随着技术的进步，低频可控震源在高精度动态监测方面的应用将越来越广泛。

5结论

本文使用国产低频可控震源KZ28LF，通过野外实验测试了其激发信号特征及在地下介质高精度动态监测中应用效果，得到的结论和认识如下：

（1）低频可控震源能持续稳定地激发频率在1.5～12Hz的线性升频信号和伪随机编码信号;出力信号和近场信号除有能量较强的基波外，还存在高阶谐波，伪随机编码谐波能量较弱。近场信号9～12Hz能量较强，1.5～9Hz相对较弱，低频信号外传能量较弱。

（2）线性升频激发模式的波形重复性最好，81%的互相关系数大于0.95，伪随机编码激发模式其次，63%的互相关系数大于0.95，单频激发模式波形重复性最差，17%大于0.85。线性升频和伪随机编码激发模式波形畸变时段集中，可通过实时质控提高激发波形的重复性。

（3）相干法和反褶积方法可用来压缩线性升频、伪随机编码和单频3种类型的激发信号，相干法得到结果的重复性和信噪比最高，反褶积法保幅和保相效果最好。

（4）经过378次叠加后，有效信号传播距离达20km。

（5）剔除不良激发班次后，线性升频和伪随机编码2种模式能以（2～7）×10-4的测量精度探测到2.3×10-3的相对波速变化。

在实验过程中，中国石油集团东方地球物理公司提供了低频可控震源，中国地震局地震科学探测台阵技术中心提供了流动观测设备，东方地球物理公司陶知非总工和祝杨高级工程师指导并参加了野外实验。审稿专家为本文提出了宝贵修改意见，在此一并表示衷心感谢！

参考文献：

顾庙元，姚佳琪，张伟，等。2016。地学长江计划安徽实验中低频可控震源地震波信号提取方法评估[J].中国地震，32（2）：356-378.

蒋生淼，王宝善，张云鹏，等。2017。噪声对气枪信号叠加效果的影响及自动数据筛选方法[J].地震研究，40（4）：534-542。

陶知非，苏振华，赵永林，等。2010。可控震源低频信号激发技术的最新进展[J].物探装备，20（1）：1-5。

陶知非，徐小剛，骆飞，等。2018。LFV3低频可控震源技术与应用效果[J].物探装备，28（1）：1-3。

陶知非，徐小刚。2017。再论可控震源输出信号畸变的问题[J].物探装备，27（6）：351-355。

陶知非。1995。可控震源与高分辨率地震勘探[J].石油物探装备，5（4）：1-9.

王秋成，王梅生，孙哲，等。2019。可控震源动态扫描高效采集实时质控要点分析[J].物探装备，29（3）：141-146。

王伟涛，王宝善。2012。基于聚类分析的多尺度相似地震快速识别方法及其在汶川地震东北端余震序列分析中的应用[J].地球物理学报，55（6）：1952-1962。

谢凡，夏开文，黄会宝，等。2020。基于多重散射波波速变化的滑坡实时监测方法与应用研究[J].岩石力学与工程学报，39（11）2274-2282.

杨承先。1983。河北徐水一文安地區第三纪伸展断裂的地质特征及其活动性分析[J].地震，（5）：34-36，45。

杨微，王宝善，葛洪魁，等。2013。精密控制机械震源特征及信号检测方法[J]中国石油大学学报（自然科学版），37（1）：50-69。

张元生，王宝善，陈颙，等。2017。两次强震发生前后主动源观测走时数据的变化[J].地球物理学报，60（10）：3815-3822。

Bensen G D.Ritzwoller MH.BarminMp. et a.2007. Processing seismic ambient noise data to obtain reliable broad-band surface wave dis-persion measurements [ J].Geophysieal Journal International， 169（3）：1239-1260.

Brenguier F， Campillo M， Takeda T， et al.2014. Mapping pressurized vol-canic fluids from induced crustal seismic velocity drops[ J]. Sci-ence，345（6192）：80-82.

Brittle KF， Lines L R， Dey A K.2001.Vibroseis deconvolution： a com-parison of cross-correlation and frequeney-domain sweep deconvolution]. Geophysical Prospecting， 49（6）： 675-686.

CaoHT.2016. Comparisons of seismic interferometry by cross correla-tion， deconvolution and cross coherence [ D]. Houghton： Michigan Technological University

Chaves EJ， Schwartz SY， Abercrombie R E.2020. Repeating earthquakes record fault weakening and healing in areas of megathrust postseismicslipLJ]. Science Advances， 6（32）： 1-8.

Chen Y， Wang B S， Yao H J.2017. Seismic airgun exploration of conti-nental crust structures[ J]. Science China Earth Seiences， 60（10）1739-1751.

Clymer R W， McEvilly TV.1981. Travel-time monitoring with vibroseis LJ. Bulletin of the Seismological Society of America， 71（6）： 1903-1927.

Cunningham A B.1979. Some altemate vibrator signalsJ]. Geophysics 44：1901-1921

Dean T.2014. The use of pseudorandom sweeps for vibroseissurveys[J Geophysical Prospecting， 62（1）： 50-74.

Godfrey HJ， Fry B， Savage M K.2017. Shear-wave veloeity structure of the Tongariro Voleanie Centre， New Zealand Fast Rayleigh and slow Love waves indicate strong shallow anisotropylJ]. Journal of volean-ology and Geothermal Research 336：33-50

Hillers G， Ben-Zion Y， Campillo M， et al.2015. Seasonal variations of seismie velocities in the San Jacinto fault area observed with ambient seismic noise [ J. Geophysical Journal International， 202（2）： 920-932.

Ikuta R. Yamaoka K， Miyakawa K， et al.2002. Continuous monitoring of propagation veloeity of seismie wave using ACROSS[ J]. Geophysical Research Letters 29（13）： 1627.

Kennett BLN.2000. RESEARCH NOTE： Stacking three-component seis-mograms[ J. Geophysical Journal International， 141（1）： 263-269

Klauder JR.1960. The design of radar signals having both high range res-olution and high velocity resolution[ J]. Bell System Technieal Jour-nal，39（4）：809-820.

Komeev VA， MeEvilly TV， Karageorgi E D.2000. Seismological studies at Parkfield VIll： Modeling the observed travel-time changes[J]Bulletin of the Seismological Society of America， 90（3）： 702-708

Krohn C， Johnson M， Ho R.2010.Vibroseis productivity： shake and go [ J. Geophysical Prospecting， 58（1）： 101-122

Lance GN， Williams WT.1967. A general theory of classificatory sorting strategies：1. hierarchical systems[ J]. The Computer Journal， 9（4 373-380

Lebedev av.beresney IA.2004. Nonlinear distortion of signals radiated by vibroseissources[ J].Geophysies， 69（4）： 877-1103.

Li L， Niu F L， Chen oF. et a.2017. Post seismic veloeity changes a-long the 2008 M7.9 Wenchuan earthquake rupture zone revealed by S coda of repeating events [ J]. Geophysical Journal International 208（2）：1237-1249.

Liu ZK. Huang JL， Peng zG， et al.2014. Seismic velocity changes in the epicentral region of the 2008 Wenchuan earthquake measured from three-component ambient noise correlation techniques [ J Geophysical Research Letters， 41（1）： 37-42.

MaoSJ， Campillo M， Van der Hilst R D， et al.2019. High temporal reso-lution monitoring of small variations in erustal strain by dense seis-mic Arrays[ J]. Geophysical Research Letters， 46（1）： 128-137.

MeCartney JS， Cox B R.2013. Role of strain magnitude on the deforma-tion response of geosynthetic - reinforced soil layers[ J].Geosynthel-ics International， 20（3）： 174-190

Mehta K.Snieder r.graizer V.2007. Downhole receiver funetion： a case study [ j]. Bulletin of the Seismological Society of America， 97（5）1396-1403.

Nagarajappa N， Wilkinson D.2010. Source measurement effect on high fidelity vibratory seismic separation[ J]. Geophysical Prospecting， 58（1）：55-67.

Niu F L， Silver PG， Daley TM， et al.2008.Preseismic velocity changes observed from active source monitoring at the Parkfield saFod drill site[J].Nature ，454（7201）：204-208.

Niu F L. silver pg.nadeau r m. et al.2003. Migration of seismic scat-terers associated with the 1993 Park field aseismie transient event [J].Nature ，426（6966）：544-548.

Peng ZG， Ben - Zion Y.2006.Temporal changes of shallow seismic velocity around the KaradereDiizce Branch of the North Anatolian Fault and strong ground motion [ J]. Pure and Applied Geophysics 163（2）：567-600.

Pevzner R， Shulakova V， Kepie A， et al.2011. Repeatability analysis of land time-lapse seismic data： CO2 CRC Otway pilot project case study [ J]. Geophysical Prospecting， 59（1）： 66-77.

Poletto F， Schleifer A， Zgaue F， et al.2016. Acquisition and deconvolution of seismic signals by different methods to perform direct ground force measurements [ J]. Journal of Applied Geophysies， 135（SI）191-203.

Rowe CA， Aster R C， Borchers B， et al.2002. An automatic， adaptive algorithm for refining phase picks in large seismie data sets[].Bul-letin of the Seismological Society of America， 92（5）： 1660-1674.

Sallas J.1984. Seismic vibrator control and the down going P-wave[Geophysics， 49：732-740

Sallas J.2010. How do hydraulic vibrators work？ A look inside the black box[ J]. Geophysical Prospecting， 58（1）： 3-17.

Silver PG， Daley TM， Niu F L， et a.2007. Active source monitoring of cross-well seismic travel time for stress - induced changes [ J.Bul-letin of the Seismological Society of America， 97（1）： 281-293

Sneath PHA， Sokal RR. Freeman WH.1973. Numerical taxonomy. The principles and practice of numerical classification[ M]. United states of America： W H freeman and company

Son M， Cho C S， Shin JS， et al.2018. Spatiotemporal distribution of events during the first three months of the 2016 Gyeongju， Korea Earthquake Sequence[ J. Bulletin of the Seismological Society of A-merica ，108（1）：210-217.

Tal B. Bencze A. Zoletnik s. et al.2011.Cross - correlation based time delav estimation for turbulent fow velocity measurements. Statistical considerations[ J]. Physics of Plasmas， 18（12）： 122304.

Wang Bs， Yang w， Wang w T， et al.2020.Diumal and semidiumnal P-and S-Wave velocity changes measured using an airgun source[J]Journal of Geophysical Research： Solid Earth， 125（1）：e2019 JB018218.

Wang b S， Zhu P， Chen Y， et al.2008. Continuous subsurface veloeity measurement with coda wave interferometry [ J. Journal of Geophysi-cal research： Solid Earth， 113（ B12）： B12313.

Wapenaar K， Draganov D， Snieder R. et al.2010.Tutorial on seismic interferometry： Part 1- Basic principles and applications [ J]. Geo-physics ，75（5）：195-209.

Wapenaar K， Fokkema J.2006. Green's function representations for seis-mic interferometry [ J]. Geophysics， 71（4）： S133-SI46

WeiZH， Phillips TF， Hall MA.2010. Fundamental discussions on seis-mic vibrators[ J]. Geophysics， 75（6）： W13-W25

WeiZH， Phillips TF.2013. On the generation of low frequeneies with modern seismic vibrators[ J. Geophysics， 78（2）： WA91-WA97.

Yamamura K， Sano O， Utada H， et al.2003.Long-term observation of in situ seismie velocity and attenuation [ J]. Journal of Geophysica Research： Solid Earth， 108（ B6）： 2317.

Yang w， Wang Bs， Yuan SY， et al.2018. Temporal variation of seismic-wave velocity associated with groundwater level observed by a down-hole airgun near the Xiaojiang Fault Zone [ J]. Seismological Research Letters， 89（3）： 1014-1022

Zaliapin I， Ben-Zion Y.2013. Earthquake clusters in southemn California Il： Classification and relation to physical properties of the crust[J]Journal of Geophysical Research： Solid Earth， 118（6）： 2865-2877.

Zhan Zw， Tsai VC， Clayton .2013. Spurious velocity changes caused by temporal variations in ambient noise frequency content J. Geophysical Joumnal International， 194（3）： 1574-1581

Signal Characteristics of Low Frequency Vibroseis and Its Application to High Precision Dynamic Monitoring

WANG Liwei.2.3. LI Li， YANG Wei， WANG Baoshan， HUANG Liufang

（1. Institute of Geophysics， China Earthquake Administration， Beiing 100081， China）

（2. CEA Key Laboratory of earthquake Monitoring and Disaster Mitigation Technology，Guangdong Earthquake Agency， Guangzhou 510070， Guangdong， China）

（3. Guangdong Provincial Key Laboratory of earthquake Early Warning and Safety Diagnosis ofMajor Projects， Guangdong Earthquake Agency， Guangzhou 510070， Guangdong， China）

（4. School of Earth and Space Sciences， University of Science and Technology of China， Hefei 230026， Anhui， China）

Abstract

The low frequency vibroseis can generate broad band， low energy density and high repeatable signals with fre-quencies as low as 1.5 Hz， which is particularly suitable for high resolution exploration and regional seismological research. In order to evaluate its signal characteristics and feasibility in high precision dynamic monitoring， we con-duct a field experiment on KZ28 LF low frequency vibroseis. We found that it can stably generate low frequency sig-nals in 1.5～12 Hz in upsweeping and pseudorandom sweeping mode， the near field energy is strong in 9.12 Hz and weak in 1.5-9 Hz， and the waveform correlation coefficient is greater than 0.95， accounting for 81o and 63o respectively， but it is still difficult to put sufficient energy into the ground in low frequency band. The signal repeatability is low and the harmonic energy is strong in single frequency excitation mode. Both the coherent and de-convolution method can successfully compress the source wavelet and restore the interpretable record， but the re-peatability and signal-to - noise ratio of coherent method is higher， and the deconvolution result can keep a high-er fidelity in phase and amplitude. After phase - weighted stacking， the max recording offsets can reach more than 20 km， and the monitoring precision of seismic velocity changes can reach up to .10. The result can provide a reference for high resolution monitoring of active fault zones， earthquake nucleation process and land slip.

Keywords： low frequency vibroseis; cluster analysis; deconvolution; phase weighted stack; velocity changes; high precision dynamic monitoring